Discrete Math 4 1 The Apportionment Problem A

Discrete Math 4. 1 – The Apportionment Problem: A special kind of fair division. – What if you can’t divide the indivisible objects? – Some will get their “fair share” and some will not… – So we need some methods to solve this dilemma

What do we use Apportionment Methods for? Congressional Seats Apportion Nurses to shifts at a hospital Apportion Calls to a switch board Apportion subway cars to a subway system Apportion planes to routes

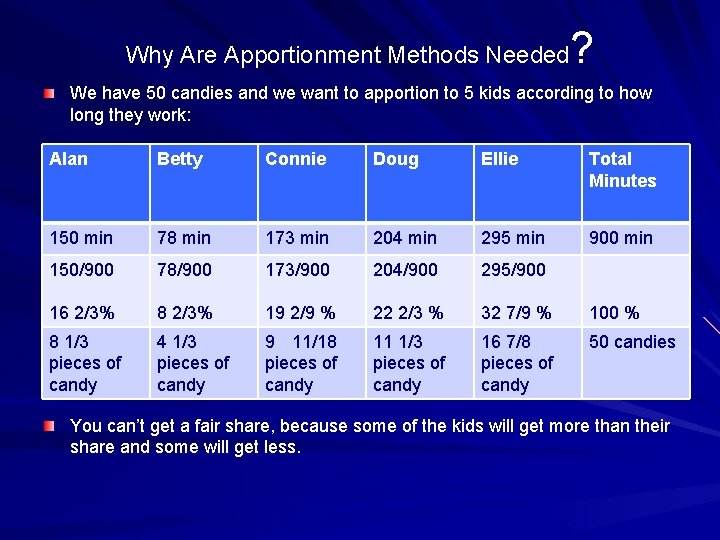
? Why Are Apportionment Methods Needed We have 50 candies and we want to apportion to 5 kids according to how long they work: Alan Betty Connie Doug Ellie Total Minutes 150 min 78 min 173 min 204 min 295 min 900 min 150/900 78/900 173/900 204/900 295/900 16 2/3% 8 2/3% 19 2/9 % 22 2/3 % 32 7/9 % 100 % 8 1/3 pieces of candy 4 1/3 pieces of candy 9 11/18 pieces of candy 11 1/3 pieces of candy 16 7/8 pieces of candy 50 candies You can’t get a fair share, because some of the kids will get more than their share and some will get less.

Discrete Math 4. 2 – Standard Divisor: Population (P), Number of seats to be apportioned (M), P/M is the standard divisor. – Standard Quota: fraction of the total number of seats that each state would be entitled to if fractional seats were possible. State X’s population / SD. – Lower Quota: Standard quota rounded down. – Upper Quota: Standard quota rounded up.

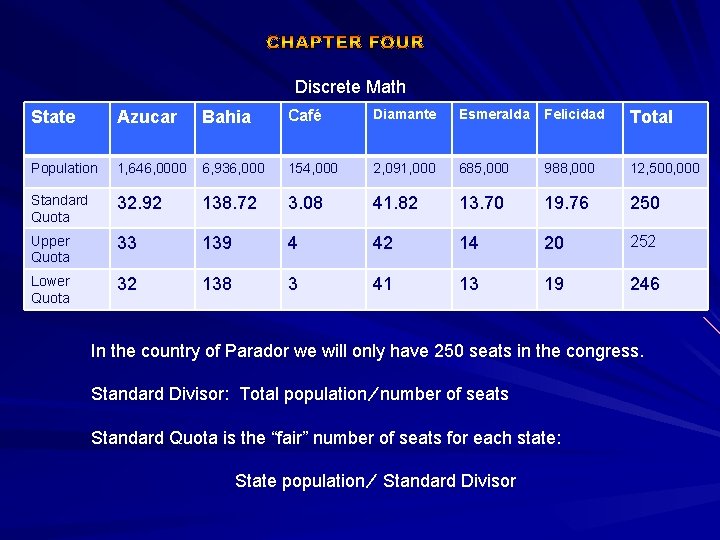
Discrete Math State Diamante Esmeralda Café Azucar Republic. Bahia of Parador: Population Data by State Felicidad Total Population 1, 646, 0000 6, 936, 000 154, 000 2, 091, 000 685, 000 988, 000 12, 500, 000 Standard Quota 32. 92 138. 72 3. 08 41. 82 13. 70 19. 76 250 Upper Quota 33 139 4 42 14 20 252 Lower Quota 32 138 3 41 13 19 246 In the country of Parador we will only have 250 seats in the congress. Standard Divisor: Total population ∕ number of seats Standard Quota is the “fair” number of seats for each state: State population ∕ Standard Divisor

4. 3 Discrete Math – Hamilton’s method and the Quota rule Step 1: Calculate each state’s standard quota. Step 2: Give each state it’s lower quota. Step 3: Give the surplus to the states with the largest fractional parts. Fails Neutral criteria: Every state has the same opportunity for favorable apportionment (Favors larger states). Violates (Alabama paradox, Population paradox, New. State paradox) To be continued…

Discrete Math 4. 3 (Continued. . . ) – Quota rule: Apportionment should be either its upper quota or its lower quota. An apportionment method that guarantees that every state will be apportioned either to its lower quota or its upper quota satisfies the rule. Violations: Lower-quota violations and upper-quota violations. To be continued…

4. 4 Discrete Math – Alabama paradox: An increase in the total number of seats being apportioned, in and of itself, forces a state to lose one of its seats.

Discrete Math 4. 5 – Population Paradox: Occurs when a state X loses a seat to the state Y even though X’s population grew at a higher rate than Y’s. – New State Paradox: The addition of a new state with its fair share of seats affects the apportionment of other states. – * Paradoxes occur in Hamilton’s method only* – * Following methods violate quota rule*

Discrete Math 4. 6 – Jefferson’s Method: We need to use a modified divisor (trial and error) that will give us new modified quotas that, when rounded down, will total the exact number of seats to be apportioned. Step 1: Find the modified divisor (D, smaller than the standard divisor) such that when each state’s modified quota is rounded down, the total is the exact number of seats to be apportioned. Step 2: Apportion to each state it’s modified lower quota. Violates (Upper Quota Rule) To be continued…

Discrete Math 4. 6 – Jefferson’s Method was the very first apportionment method used by the U. S. House of Representatives. (Violates the quota rule).

Discrete Math 4. 7 – Adam’s Method Step 1: Find the modified divisor D such that when each state’s modified quota is rounded upward, the total is the exact number of seats to be apportioned. Step 2: Apportion to each state its modified upper quota. – Adam’s violations are all lower quota violations.

Discrete Math 4. 8 – Webster’s Method: Round quotas to the nearest integer. Step 1: Find the modified divisor D such that when each state’s modified quota is rounded the conventional way, the total is the exact number of seats to be apportioned. Step 2: Apportion to each state its modified quota rounded the conventional way. May violate either quota rule, but rare. Comes Closest to satisfying all main requirements for fairness. To be continued…

Discrete Math 4. 8 – Balinski and Young’s impossibility theorem: There cannot be a perfect apportionment method. Any method that does not violate the quota rule must produce paradoxes and vice-versa.

Discrete Math Appendix 1 – The Huntington-Hill Method: Comparable to the Webster method: Find modified quotas and round some down and some upward. The difference is the cutoff point for rounding. L: Lower quota L+1: upper quota. Cutoff for Webster’s: L + (L + 1) / 2 – “Arithmetic mean” Cutoff for Huntington-Hill: Square root of (L x (L+1)) – “Geometric mean”

Discrete Math