Discrete Math 1302022 1 Part 1 The Fundamentals

Discrete Math 1/30/2022 1

Part #1: The Fundamentals of Logic 2

Part #1: Foundations of Logic Mathematical Logic is a tool for working with compound statements. 3

Foundations of Logic: Overview Section 1. 1: Logic • Propositional logic: It deals with propositions. • Predicate logic: it deals with predicates. 4

Topic #1 – Propositional Logic Definition of a Proposition Definition: A proposition (denoted p, q, r, …) is a statement (i. e. , a declarative sentence) having a truth value that’s either true (T) or false (F). But it is never both, neither, or somewhere “in between!” Note: (commands and questions are not propositions) 5

Topic #1 – Propositional Logic Examples of Propositions • “It is raining. ” (In a given situation. ) • “Amman is the capital of Jordan” • “ 1 + 2 = 3” But, the following are NOT propositions: • “Who’s there? ” (question) • “La la la. ” (meaningless) • “Just do it!” (command) • “ 1 + 2” (expression with a non-true/false value) • “ 1+2=x” (expression with unknown value: x) 6

Topic #1. 0 – Propositional Logic: Operators / Connectives An operator or connective combines one or more operand expressions into a larger expression. (E. g. , “+” in numeric exprs. ) • Unary operators take 1 operand (e. g. , − 3); binary operators take 2 operands (eg 3 4). • Propositional or Boolean operators operate on propositions (or their truth values) instead of on numbers. 7

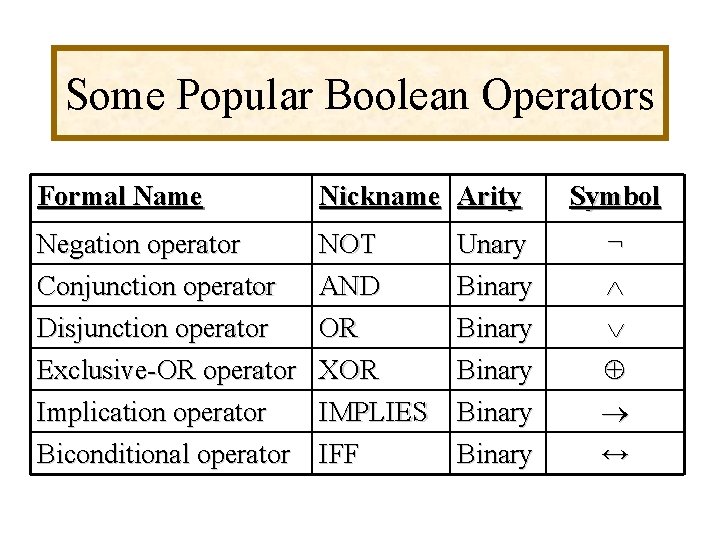
Topic #1. 0 – Propositional Logic: Operators Some Popular Boolean Operators Formal Name Nickname Arity Symbol Negation operator Conjunction operator NOT AND Unary Binary ¬ Disjunction operator Exclusive-OR operator Implication operator Biconditional operator OR XOR IMPLIES IFF Binary ↔ 8

Topic #1. 0 – Propositional Logic: Operators The Negation Operator Definition: Let p be a proposition then ¬p is the nagation of p (Not p , it is not the case that p) E. g. If p = “London is a city. ” then ¬p = “London is not a city. ” or “ it is not the case that London is a city. ” The truth table for NOT: T : ≡ True; F : ≡ False “: ≡” means “is defined as” Operand column Result column 9

Topic #1. 0 – Propositional Logic: Operators The Conjunction Operator Definition: Let p and q be propositions, the proposition “p AND q” denoted by (p q) is ND called the conjunction of p and q. E. g. If p=“I will have salad for lunch. ” and q=“I will have steak for dinner. ”, then p q=“I will have salad for lunch and I will have steak for dinner. ” Remember: “ ” points up like an “A”, and it means “ ND” 10

Topic #1. 0 – Propositional Logic: Operators Conjunction Truth Table Operand columns • Note that a conjunction p 1 p 2 … pn of n propositions will have 2 n rows in its truth table. “AND”, ”but”, ”in addition to”, ”moreover” 11

Topic #1. 0 – Propositional Logic: Operators The Disjunction Operator Definition: Let p and q be propositions, the proposition “p OR q” denoted by (p q) is called the disjunction of p and q. p=“My car has a bad engine. ” q=“My car has a bad carburetor. ” p q=“Either my car has a bad engine, or my car has a bad carburetor. ” 12

Topic #1. 0 – Propositional Logic: Operators Disjunction Truth Table • Note that p q means that p is true, or q is true, or both are true! • So, this operation is also called inclusive or, because it includes the possibility that both p and q are true. Note difference from AND 13

Topic #1. 0 – Propositional Logic: Operators The Exclusive Or Operator The binary exclusive-or operator “ ” (XOR) combines two propositions to form their logical “exclusive or” (exjunction? ). p = “I will earn an A in this course, ” q = “I will drop this course, ” p q = “I will either earn an A in this course, or I will drop it (but not both!)” 14

Topic #1. 0 – Propositional Logic: Operators Exclusive-Or Truth Table • Note that p q means that p is true, or q is true, but not both! • This operation is called exclusive or, because it excludes the possibility that both p and q are true. Note difference from OR. 15

Topic #1. 0 – Propositional Logic: Operators Natural Language is Ambiguous Note that English “or” can be ambiguous regarding the “both” case! “Pat is a singer or Pat is a writer. ” - “Pat is a man or Pat is a woman. ” - Need context to disambiguate the meaning! For this class, assume “or” means inclusive. 16

Topic #1. 0 – Propositional Logic: Operators A Simple Exercise Let p=“It rained last night”, q=“The sprinklers came on last night, ” r=“The grass was wet this morning. ” Translate each of the following into English: ¬p = “It didn’t rain last night. ” r ¬p = “The grass was wet this morning, and it didn’t rain last night. ” ¬ r p q = “Either the grass wasn’t wet this morning, or it rained last night, or the sprinklers came on last night. ” 17

Topic #1. 0 – Propositional Logic: Operators Nested Propositional Expressions • Use parentheses to group sub-expressions: “I just saw my old friend, and either he’s grown or I’ve shrunk. ” = f (g s) – (f g) s would mean something different – f g s would be ambiguous • By convention, “¬” takes precedence over both “ ” and “ ”. (¬, , ) – ¬s f means (¬s) f , not ¬ (s f) 18

Topic #1. 0 – Propositional Logic: Operators The Implication Operator hypothesis conclusion The implication p q states that p implies q. I. e. , If p is true, then q is true; but if p is not true, then q could be either true or false. E. g. , let p = “You get 100% on the final. ” q = “You will get an A” p q = “If you get 100% on the final, then you will get an A. ” 19

Topic #1. 0 – Propositional Logic: Operators Implication Truth Table • p q is false only when p is true but q is not true. • p q does not say that p causes q! • p q does not require that p or q are ever true! • E. g. “(1=0) pigs can fly” is TRUE! The only False case! 20

Topic #1. 0 – Propositional Logic: Operators Examples of Implications • “If this lecture ever ends, then the sun will rise tomorrow. ” True or False? • “If Tuesday is a day of the week, then I am a penguin. ” True or False? • “If 1+1=6, then Bush is president. ” True or False? 21

P Q has many forms in English Language: • • "P implies Q" “Q whenever P” " If P, Q" “Q follows from P” "If P, then Q" "P only if Q“ "P is sufficient for Q" "Q if P" "Q is necessary for P" “Q when P" 22

Topic #1. 0 – Propositional Logic: Operators Converse, Inverse, Contrapositive Some terminology, for an implication p q: • Its converse is: q p. • Its inverse is: ¬p ¬q. • Its contrapositive: ¬q ¬ p. 23

Topic #1. 0 – Propositional Logic: Operators Biconditional Truth Table In English: • "P if and only if Q" • "If P, then Q, and conversely" • "P is sufficient and necessary for Q“ • Written p q 24

Translation English Sentences into Logical Expressions • If you are a computer science major or you are not a freshman, P Q then you can access the internet from campus. R is translated to: (P Q) R 25

Precedence of Logical operators Operator ¬ Precedence 1 2 3 4 5 26

Topic #1. 1 – Propositional Logic: Equivalences (Section 1. 2)Propositional Equivalence Tautologies and Contradictions A tautology is a compound proposition that is always true. Ex. p p A contradiction is a compound proposition that is false Ex. p p Other compound props. are contingencies. Ex. P q 27

Topic #1. 1 – Propositional Logic: Equivalences Equivalence Laws • • • Identity: p T p p F p Domination: p T T p F F Idempotent: p p p Double negation: p p Commutative: p q q p Associative: (p q) r p (q r) 28

Topic #1. 1 – Propositional Logic: Equivalences More Equivalence Laws • Distributive: p (q r) (p q) (p r) • De Morgan’s: (p q) p q • Trivial tautology/contradiction: p p T p p F Augustus De Morgan (1806 -1871) 29

Implications / Biconditional Rules • • 1. P Q P Q 2. (P Q) P Q 3. P Q Q P (contrapositive) 4. P Q (P Q) (Q P) 30

Topic #1. 1 – Propositional Logic: Equivalences Proving Equivalence via Truth Tables Ex. Prove that p q ( p q). “ De Morgan’s law” TAUTOLOGY 31

Example: show that (P ( P Q) and ( P Q) are logically equivalent. 1. 2. 3. 4. 5. 6. (P ( P Q) P ( ( P) Q) P ( P Q ) ( P P) ( P Q) F ( P Q) De morgan Double negation Distributive Negation Identity 32

Topic #3 – Predicate Logic Section 1. 3 Predicates and Quantifiers Predicates Example: “x is greater than 3” has two parts: First part: x Second part: the predicate “is greater than 3” SO: x is greater than 3 can be denoted by P(x). Where x is the variable and p denotes >3. P(x): x>3 , let x=4, then P(4) is true. Example: R(x, y, z) : x+y=z then R(1, 2, 3): 1+2=3 / True 33

Quantifiers Quantification Universal Quantification Existential Quantification Universes of Discourse (U. D. s) (Domain): collection of all persons, ideas, symbols, ……… 34

The Universal Quantifier • x P(x): “ P(x) is true for all/every values of x in the universe of discourse” • Example: What is the truth value of x(x 2 ≥ x) if: UD is all real numbers- False (0. 5) this is called a counterexample If: UD is all integers - True 35

Topic #3 – Predicate Logic The Existential Quantifier x P(x) : There exists an element x in the universe of discourse such that P(x) is true • Example: Let Q(x): x=x+1, UD: all real numbers. the value of x Q(x) is false for every number x 36

Negations • x P(x) ≡ x P(x) • x Q(x) ≡ x Q(x) 37

Translation using Predicates and Quantifiers • “Every student in this class has studied math and C++ course”. UD: students in this class Translated to: x( M(x) CPP(x)) • But if the UD is all people “ For every person x, if x is a student in this class then x has studied math and C++” translated to : x (S(x) M(x) CPP(x)) 38

Example • “some student in this class has studied math and C++ course”. UD: student in this class. Translated to: x ( M(x) CPP(x)) • But if the UD: all people Translated to: x (S(x) M(x) CPP(x) ) 39

Topic #3 – Predicate Logic Free and Bound Variables • The variable is either bound or free Examples: P(x, y) x and y are free variables x P(x, y) x is bound and y is free “P(x), where x=3” is another way to bind x 40

Topic #3 – Predicate Logic Section 1. 4: Nesting of Quantifiers Example: UD: all real numbers x y (x+y = 0) false x y (x+y = 0) true (inverse) x y (x+y = 0) true y x (x+y = 0) false ﻣﺸﺘﺮﻙ 41

Translation English Sentences into Logical Expressions • Exercise: express the statement: “for every person, if a person is a female and is a parent, then this person is someone’s mother” F(x): person is a female P(x): person is a parent M(x, y): x is the mother of y Solution: x ( (F(x) P(x)) y M(x, y) ) 42