Discrete Event Systems Simulation Lecture 1 Introduction Dr

Discrete Event Systems Simulation Lecture 1: Introduction Dr. Jafar Habibi

Outline �Modeling and Simulation �What? �Why? �Uses �Taxonomy �Model Development Life Cycle

Modeling and Simulation Definitions �Model � A (usually miniature) representation of something; an example for imitation or emulation [Merriam-Webster dictionary] � A description of observed behavior, simplified by ignoring certain details. Models allow complex systems to be understood and their behavior predicted within the scope of the model, but may give incorrect descriptions and predictions for situations outside the realm of their intended use. [www. learnthat. com] �Simulation � The imitative representation of the functioning of one system or process by means of the functioning of another [Merriam. Webster dictionary]

�System: set of objects, joined to accomplish some purpose

Why Simulate? �It may be too difficult, hazardous, or expensive to observe a real, operational system �Parts of the system may not be observable (e. g. , internals of a silicon chip or biological system) Uses of simulations �Analyze systems before they are built � Reduce number of design mistakes � Optimize design �Analyze operational systems �Create virtual environments for training, entertainment

When is simulation appropriate? � Allows access to system internals that may otherwise not be observable. � Informational, organizational, and environmental changes can be � simulated, and the effect of these changes on the model’s behavior � can be observed. � Observations based on simulations give great insight into the system behavior, and it can be determined which variables are most important and how they interact. � Analytic solutions can be verified. � Simulation allows to experiment with new designs or policies prior to implementation. � Can be used for training without the cost and disruption of on-the-job learning. � The simulated system is so complex, that its interactions can be treated only through simulation

When simulation is not appropriate? �Would common sense suffice? �Is there an analytical solution? �Is it easier to perform direct measurements on a physical system? �Is there a shortage of resources for implementing the simulation? �Is there a shortage of time for getting the desired results? �Is data lacking for modeling the system and beginning a simulation study? �Is there enough time and personnel to verify and validate the model? �Are the managers’ expectations unrealistic? �Is the system too complex to be modeled?

Models in Simulation Types of models Physical models Simulation models Analytical models But why model? Understanding Improvement Optimization Decision making

Applications: System Analysis “Classical” application of simulation �Telecommunication networks �Transportation systems �Electronic systems (e. g. , microelectronics, computer systems) �Battlefield simulations (blue army vs. red army) �Ecological systems �Manufacturing systems �Logistics Focus typically on planning, system design

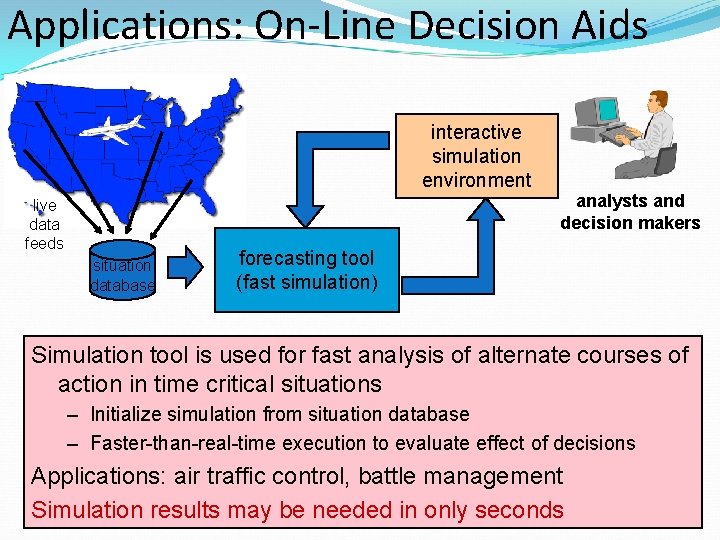
Applications: On-Line Decision Aids interactive simulation environment live data feeds situation database analysts and decision makers forecasting tool (fast simulation) Simulation tool is used for fast analysis of alternate courses of action in time critical situations – Initialize simulation from situation database – Faster-than-real-time execution to evaluate effect of decisions Applications: air traffic control, battle management Simulation results may be needed in only seconds

Applications: Virtual Environments Uses: training (e. g. , military, medicine, emergency planning), entertainment Simulations are often used in virtual environments to create dynamic computer generated entities �Adversaries and helpers in video games �Defense: Computer generated forces (CGF) �Automated forces �Semi-automated forces �Physical phenomena �Trajectory of projectiles �Buildings “blowing up” �Environmental effects on environment (e. g. , rain washing out terrain)

A Few Example Applications Wargaming: test strategies; training Earth magnetosphere: Transportation systems: understand space improved operations; weather urban planning Parallel computer systems: developing scalable software Computer communication network: protocol design

Simulation Fundamentals A computer simulation is a computer program that models the behavior of a physical system over time. �Program variables (state variables) represent the current state of the physical system �Simulation program modifies state variables to model the evolution of the physical system over time.

Defense Simulations �Types of simulation �Constructive: simulated people operating simulated equipment �Virtual: real people operating simulated equipment, �Live: real people operating real equipment �Major application areas �Analysis � Wargaming, logistics �Training � Platform level, Command level �Test and evaluation � Hardware-in-the-loop

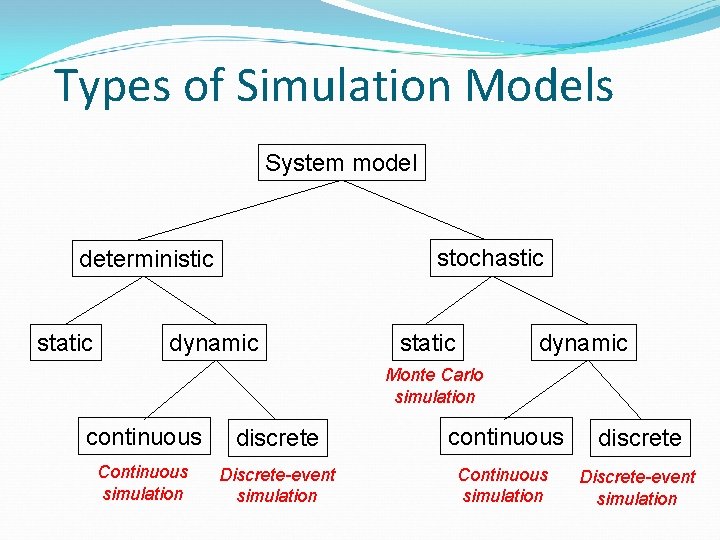
Types of Simulation Models System model stochastic deterministic static dynamic Monte Carlo simulation continuous discrete Continuous simulation Discrete-event simulation

Stochastic vs. Deterministic �Stochastic simulation: a simulation that contains random (probabilistic) elements, e. g. , �Examples � Inter-arrival time or service time of customers at a restaurant or store � Amount of time required to service a customer �Output is a random quantity (multiple runs required analyze output) �Deterministic simulation: a simulation containing no random elements �Examples � Simulation of a digital circuit � Simulation of a chemical reaction based on differential equations �Output is deterministic for a given set of inputs

Static vs. Dynamic Models �Static models �Model where time is not a significant variable �Examples � Determine the probability of a winning solitaire hand �Static + stochastic = Monte Carlo simulation � Statistical sampling to develop approximate solutions to numerical problems �Dynamic models �Model focusing on the evolution of the system under investigation over time �Main focus of this course

Continuous vs. Discrete �State of the system is viewed as changing at discrete points in time �An event is associated with each state transition � Events contain time stamp �Continuous �State of the system is viewed as changing continuously across time �System typically described by a set of differential equations

Course Overview This course is basically about going from to An actual or envisioned system • • A useful simulation model of that system Discrete event simulation Continuous simulation Monte Carlo simulation Simulation software

Course Outcomes � Recognize mathematical parameters as if they were physical variables and vice-versa � Be able to follow general mathematical concepts of derivation of engineering or scientific result and possess the mathematical skill to link those concepts � Be able to understand the relevance of the mathematical results to physical applications � Have the ability to use computational tools for finding graphical, numerical, statistical and analytic solutions to problems � Have the ability to use systems simulations appropriate to engineering practice � Be able to identify input, output, and operating variables as appropriate in various units � Be able to identify technical relationships between the input, output and variables and use the relationships to predict mutualchanges

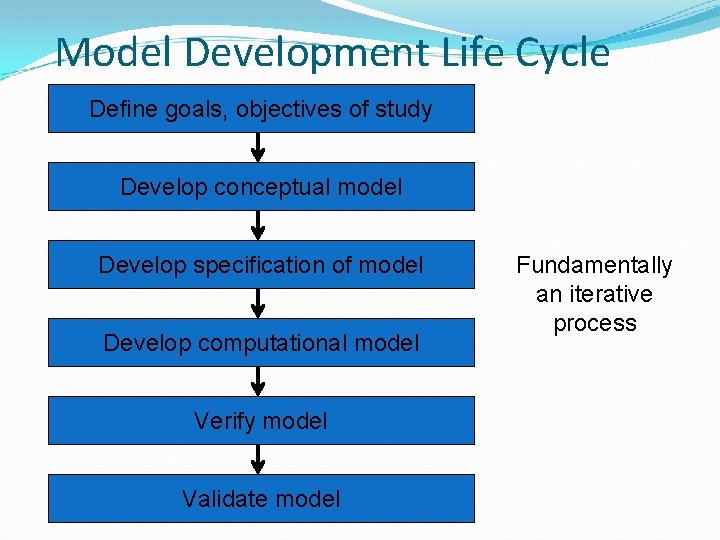
Model Development Life Cycle Define goals, objectives of study Develop conceptual model Develop specification of model Develop computational model Verify model Validate model Fundamentally an iterative process

Determine Goals and Objectives �What does you (or the customer) hope to accomplish with the model � May be an end in itself � Predict the weather � Train personnel to develop certain skills (e. g. , driving) � More often a means to an end � Optimize a manufacturing process or develop the most cost effective means to reduce traffic congestion in some part of a city �Often requires developing a business case to justify the cost � Improved efficiency will save the company $$$ � Example: electronics � Even so, may be hard to justify in lean times �Goals may not be known when you start the project! � One often learns things along the way

Develop Conceptual Model �An abstract (i. e. , not directly executable) representation of the system �What should be included in model? What can be left out? �What abstractions should be used � Level of detail � Often a variation on standard abstractions � Example: transportation � Fluid flow? � Queueing network? � Cellular automata? �What metrics will be produced by the model? �Appropriate choice depends on the purpose of the model

Develop Specification Model �A more detailed specification of the model including more specifics �Collect data to populate model �Traffic example: Road geometry, signal timing, expected traffic demand, driver behavior �Empirical data or probability distributions often used �Development of algorithms necessary to include in the model �Example: Path planning for vehicles

Develop Computational Model �Executable simulation model �Software approach �General purpose programming language �Special purpose simulation language �Simulation package �Approach often depends on need for customization and economics Where do you make your money? � Defense vs. commercial industry � �Other (non-functional) requirements �Performance �Interoperability with other models/tools/data

Verification �Did I build the model right? �Does the computational model match the specification model? �Largely a software engineering activity (debugging) �Not to be confused with correctness (see model validation)!

Validation �Did I build the right model? �Does the computational model match the actual (or envisioned) system? �Typically, compare against �Measurements of actual system �An analytic (mathematical) model of the system �Another simulation model �By necessity, always an incomplete activity! �Often can only validate portions of the model �If you can validate the simulation with 100% certainty, why build the simulation?

Summary �Modeling and simulation is an important, widely used technique with a wide range of applications �Computation power increases (Moore’s law) have made it more pervasive �In some cases, it has become essential (e. g. , to be economically competitive) �Rich variety of types of models, applications, uses �As easy (actually, easier!) to get wrong or misleading answers as it is to get useful results �Appropriate methodologies required to protect against major mistakes. Even so…

Questions? Courtesy of Professor Richard Fujimoto