DISCRETE COMPUTATIONAL STRUCTURES CSE 2353 Fall 2005 Discrete

DISCRETE COMPUTATIONAL STRUCTURES CSE 2353 Fall 2005 Discrete Mathematical Structures: Theory and Applications

CSE 2353 OUTLINE 3. Sets 2. Logic Proof Techniques Integers and Induction 4. 5. Relations and Posets 6. 7. 1. Functions Counting Principles 8. Boolean Algebra Discrete Mathematical Structures: Theory and Applications

Learning Objectives q Learn the basic counting principles— multiplication and addition q Explore the pigeonhole principle q Learn about permutations q Learn about combinations Discrete Mathematical Structures: Theory and Applications 3

Basic Counting Principles Discrete Mathematical Structures: Theory and Applications 4

Basic Counting Principles Discrete Mathematical Structures: Theory and Applications 5

Basic Counting Principles q There are three boxes containing books. The first box contains 15 mathematics books by different authors, the second box contains 12 chemistry books by different authors, and the third box contains 10 computer science books by different authors. q A student wants to take a book from one of the three boxes. In how many ways can the student do this? Discrete Mathematical Structures: Theory and Applications 6

Basic Counting Principles q Suppose tasks T 1, T 2, and T 3 are as follows: q T 1 : Choose a mathematics book. q T 2 : Choose a chemistry book. q T 3 : Choose a computer science book. q Then tasks T 1, T 2, and T 3 can be done in 15, 12, and 10 ways, respectively. q All of these tasks are independent of each other. Hence, the number of ways to do one of these tasks is 15 + 12 + 10 = 37. Discrete Mathematical Structures: Theory and Applications 7

Basic Counting Principles Discrete Mathematical Structures: Theory and Applications 8

Basic Counting Principles q Morgan is a lead actor in a new movie. She needs to shoot a scene in the morning in studio A and an afternoon scene in studio C. She looks at the map and finds that there is no direct route from studio A to studio C. Studio B is located between studios A and C. Morgan’s friends Brad and Jennifer are shooting a movie in studio B. There are three roads, say A 1, A 2, and A 3, from studio A to studio B and four roads, say B 1, B 2, B 3, and B 4, from studio B to studio C. In how many ways can Morgan go from studio A to studio C and have lunch with Brad and Jennifer at Studio B? Discrete Mathematical Structures: Theory and Applications 9

Basic Counting Principles q There are 3 ways to go from studio A to studio B and 4 ways to go from studio B to studio C. q The number of ways to go from studio A to studio C via studio B is 3 * 4 = 12. Discrete Mathematical Structures: Theory and Applications 10

Basic Counting Principles Discrete Mathematical Structures: Theory and Applications 11

Basic Counting Principles q Consider two finite sets, X 1 and X 2. Then q This is called the inclusion-exclusion principle for two finite sets. q Consider three finite sets, A, B, and C. Then q This is called the inclusion-exclusion principle for three finite sets. Discrete Mathematical Structures: Theory and Applications 12

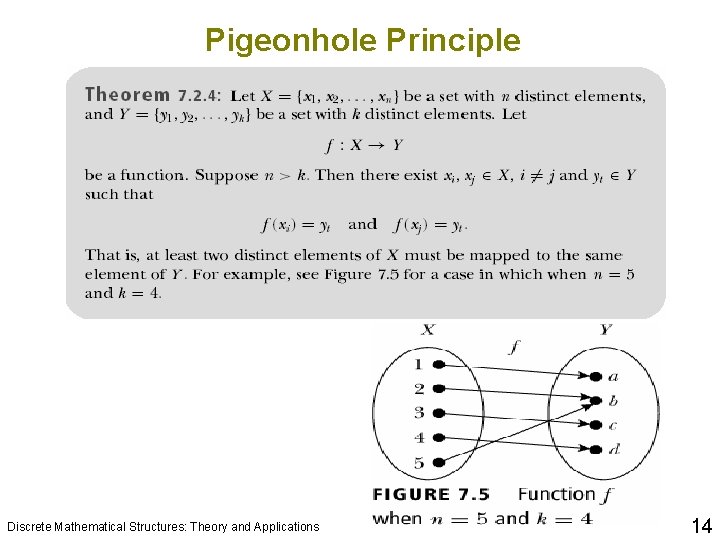
Pigeonhole Principle pigeonhole principle is also known as the Dirichlet drawer principle, or the shoebox principle. q The Discrete Mathematical Structures: Theory and Applications 13

Pigeonhole Principle Discrete Mathematical Structures: Theory and Applications 14

Discrete Mathematical Structures: Theory and Applications 15

Pigeonhole Principle Discrete Mathematical Structures: Theory and Applications 16

Permutations Discrete Mathematical Structures: Theory and Applications 17

Permutations Discrete Mathematical Structures: Theory and Applications 18

Combinations Discrete Mathematical Structures: Theory and Applications 19

Combinations Discrete Mathematical Structures: Theory and Applications 20

Generalized Permutations and Combinations Discrete Mathematical Structures: Theory and Applications 21

Generalized Permutations and Combinations Discrete Mathematical Structures: Theory and Applications 22

CSE 2353 OUTLINE 3. 4. 5. 8. Sets 2. Logic Proof Techniques Integers and Induction Relations and Posets 6. 7. 1. Functions Counting Principles Boolean Algebra Discrete Mathematical Structures: Theory and Applications

Learning Objectives q Learn about Boolean expressions q Become aware of the basic properties of Boolean algebra q Explore the application of Boolean algebra in the design of electronic circuits q Learn the application of Boolean algebra in switching circuits Discrete Mathematical Structures: Theory and Applications 24

Two-Element Boolean Algebra Let B = {0, 1}. Discrete Mathematical Structures: Theory and Applications 25

Two-Element Boolean Algebra Discrete Mathematical Structures: Theory and Applications 26

Discrete Mathematical Structures: Theory and Applications 27

Discrete Mathematical Structures: Theory and Applications 28

Discrete Mathematical Structures: Theory and Applications 29

Two-Element Boolean Algebra Discrete Mathematical Structures: Theory and Applications 30

Two-Element Boolean Algebra Discrete Mathematical Structures: Theory and Applications 31

Discrete Mathematical Structures: Theory and Applications 32

Discrete Mathematical Structures: Theory and Applications 33

Discrete Mathematical Structures: Theory and Applications 34

Discrete Mathematical Structures: Theory and Applications 35

Discrete Mathematical Structures: Theory and Applications 36

Discrete Mathematical Structures: Theory and Applications 37

Discrete Mathematical Structures: Theory and Applications 38

Boolean Algebra Discrete Mathematical Structures: Theory and Applications 39

Boolean Algebra Discrete Mathematical Structures: Theory and Applications 40

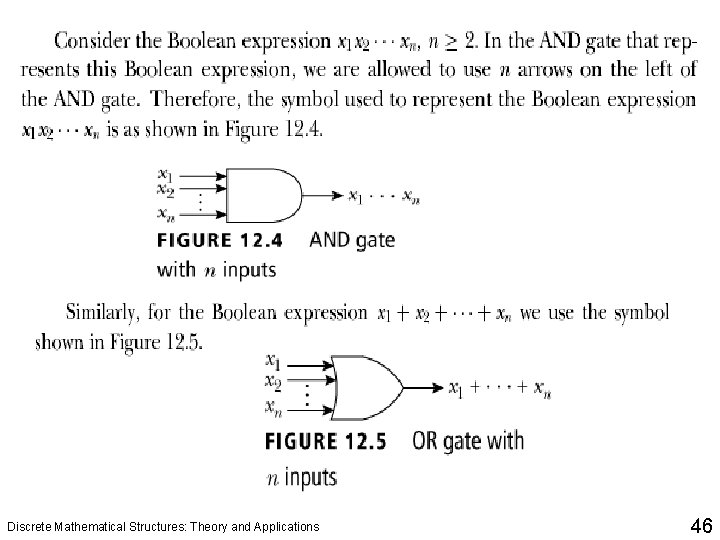
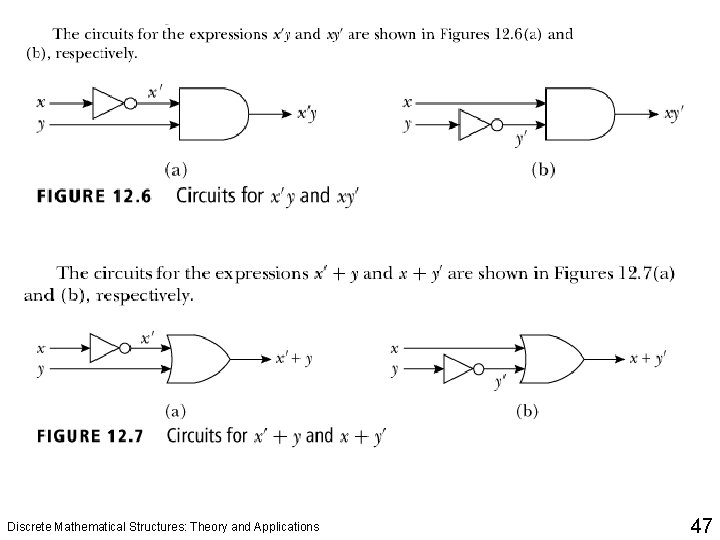
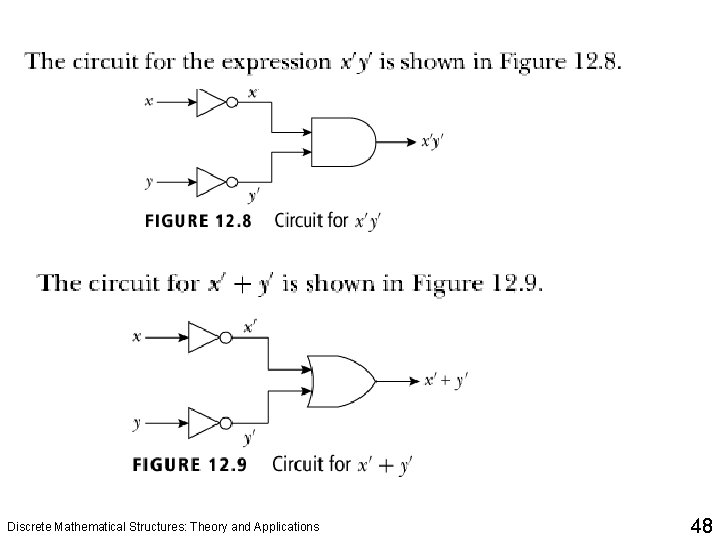
Logical Gates and Combinatorial Circuits Discrete Mathematical Structures: Theory and Applications 41

Logical Gates and Combinatorial Circuits Discrete Mathematical Structures: Theory and Applications 42

Logical Gates and Combinatorial Circuits Discrete Mathematical Structures: Theory and Applications 43

Logical Gates and Combinatorial Circuits Discrete Mathematical Structures: Theory and Applications 44

Discrete Mathematical Structures: Theory and Applications 45

Discrete Mathematical Structures: Theory and Applications 46

Discrete Mathematical Structures: Theory and Applications 47

Discrete Mathematical Structures: Theory and Applications 48

Discrete Mathematical Structures: Theory and Applications 49

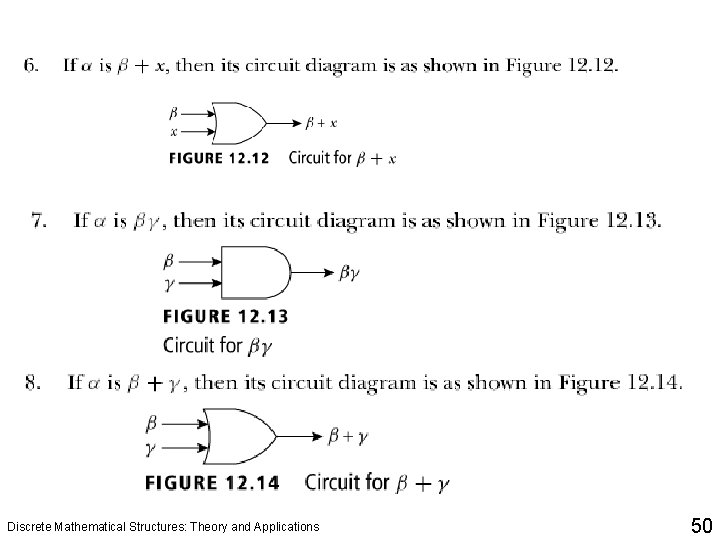
Discrete Mathematical Structures: Theory and Applications 50

Discrete Mathematical Structures: Theory and Applications 51

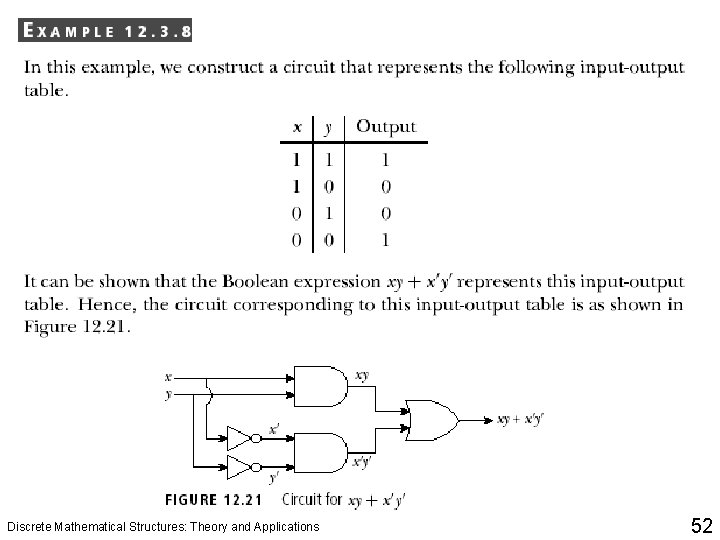
Discrete Mathematical Structures: Theory and Applications 52

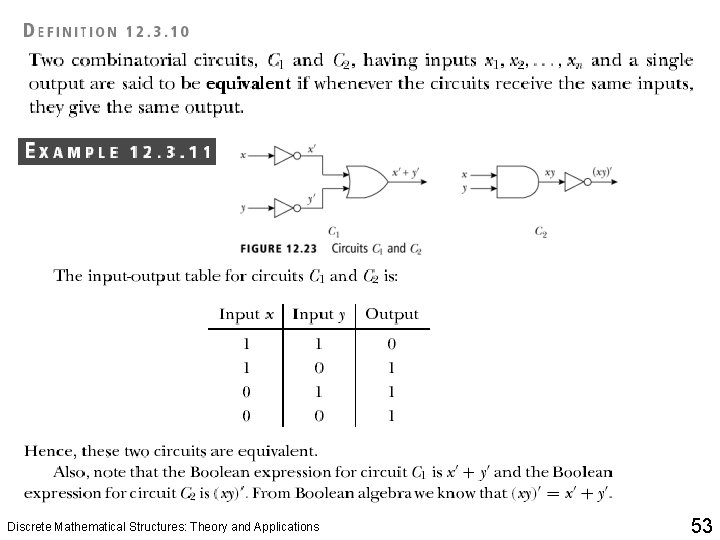
Discrete Mathematical Structures: Theory and Applications 53

Discrete Mathematical Structures: Theory and Applications 54

Discrete Mathematical Structures: Theory and Applications 55

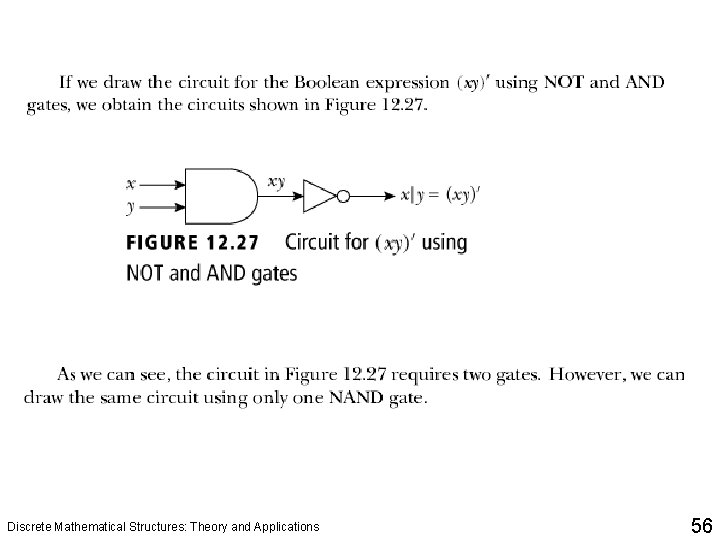
Discrete Mathematical Structures: Theory and Applications 56

Discrete Mathematical Structures: Theory and Applications 57

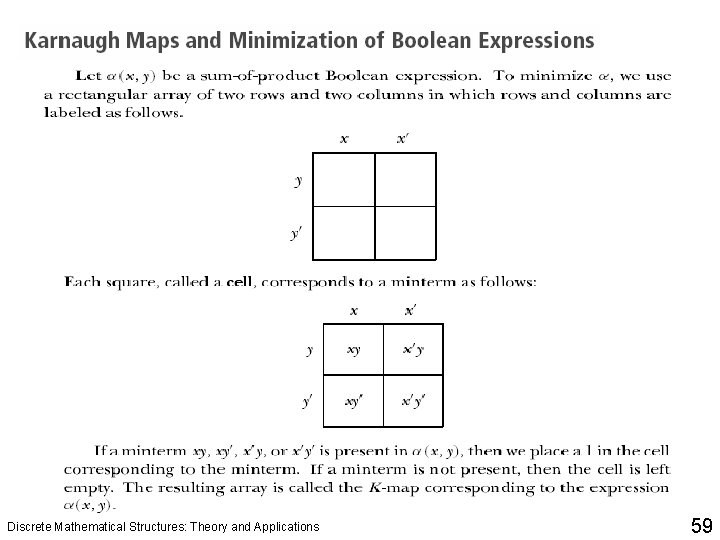
Discrete Mathematical Structures: Theory and Applications 58

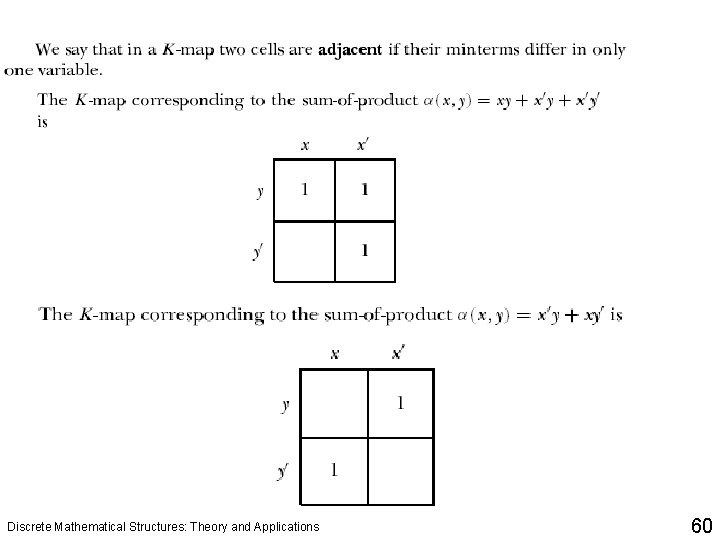
Discrete Mathematical Structures: Theory and Applications 59

Discrete Mathematical Structures: Theory and Applications 60

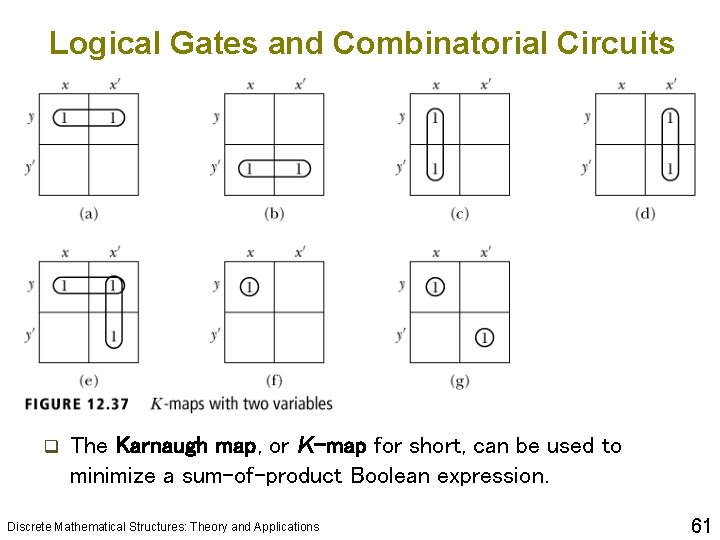
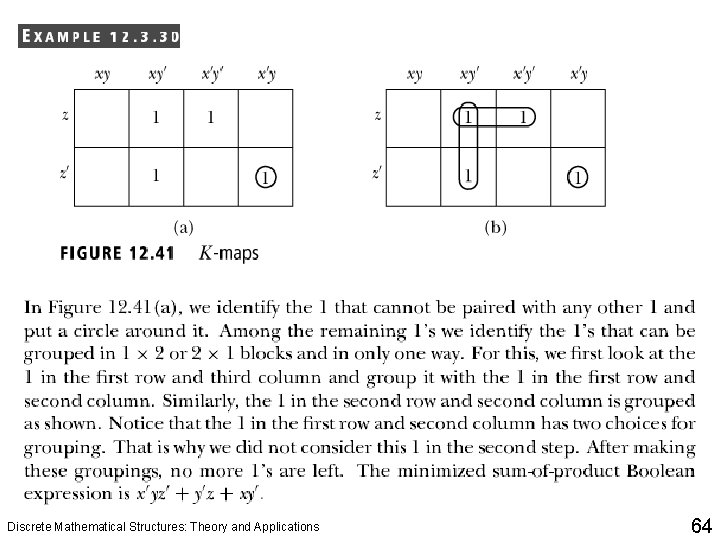
Logical Gates and Combinatorial Circuits q The Karnaugh map, or K-map for short, can be used to minimize a sum-of-product Boolean expression. Discrete Mathematical Structures: Theory and Applications 61

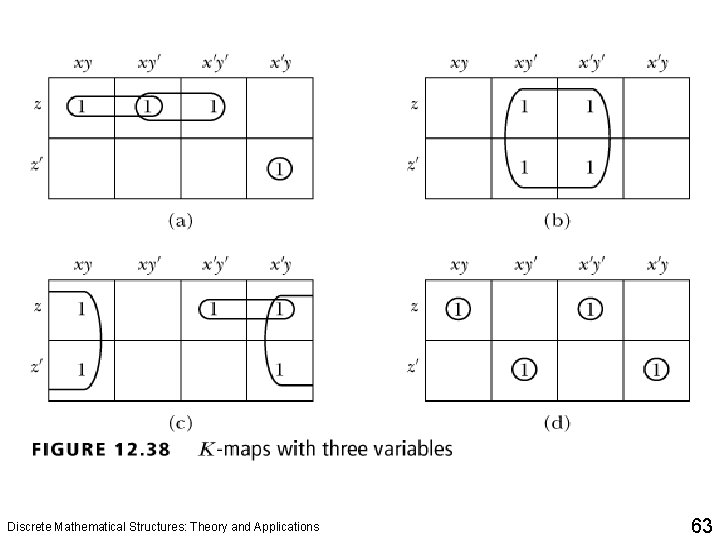
Discrete Mathematical Structures: Theory and Applications 62

Discrete Mathematical Structures: Theory and Applications 63

Discrete Mathematical Structures: Theory and Applications 64