Discovery of Electrons J J Thompson 1897 England

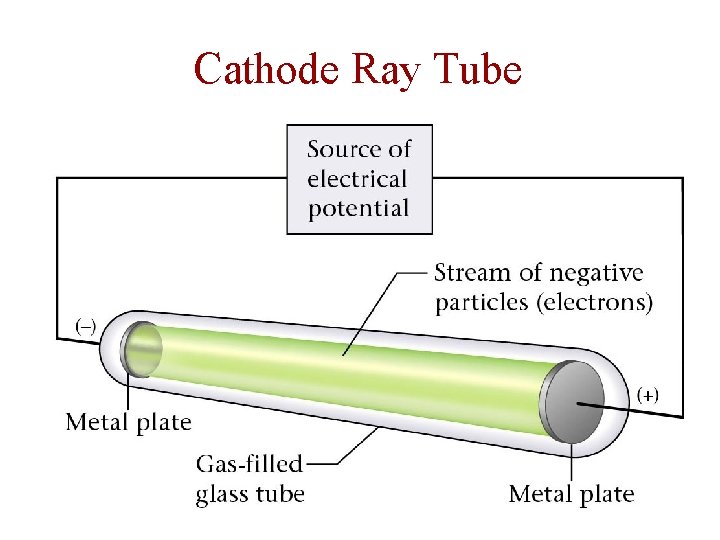
Discovery of Electrons • J. J. Thompson • 1897 England • Thompson discovered that electrons were smaller particles of an atom and were negatively charged. • Thompson knew atoms were neutrally charged, but couldn’t find the positive particle.

J. J. Thompson

Cathode Ray Tube

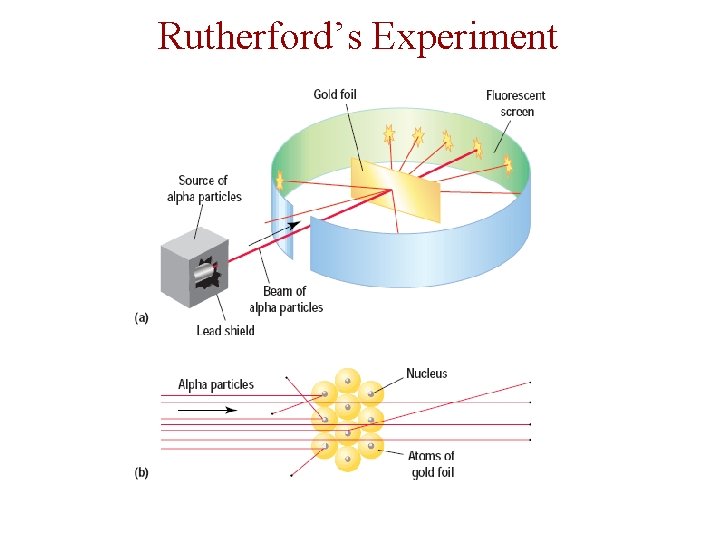
Atomic Structure I • Ernest Rutherford • 1911 England • Conducted an experiment to isolate the positive particles in an atom. Decided that the atoms were mostly empty space, but had a dense central core that was positive. • He knew that atoms had positive and negative particles, but could not decide how they were arranged.

Ernest Rutherford

Rutherford’s Experiment

What is Light? • Light is how we refer to electromagnetic radiation. • This applies not only to the light we can see, but also infrared light, UV light, microwaves, radio waves, x-rays and so forth.

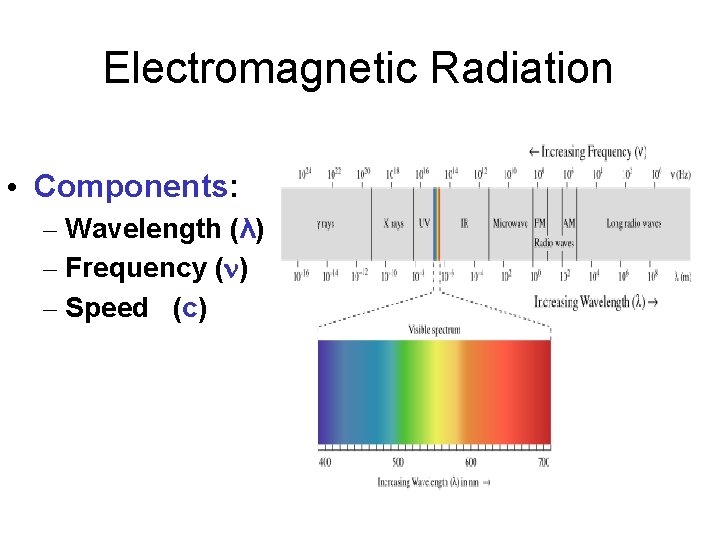
Electromagnetic Radiation • Components: – Wavelength (λ) – Frequency (n) – Speed (c)

Electromagnetic Radiation (1) Radio Waves -- used in communications (2) Microwaves-- broadcasts TV signals and used to cook food. (3) Infrared (IR) -- we feel this as heat. Snakes and owls can “see” this. infrared image of a cat infrared image of heating pipes under a floor

Infrared Vision

Electromagnetic Radiation (4) Visible Light -- the only radiation we can detect with our eyes. It can be separated into the colors of the spectrum with a prism. ROYGBIV (5) Ultraviolet (UV) -- gives you a sunburn. Bees can “see” this; Some of this radiation from the sun gets blocked by the ozone layer. flower photo under normal light flower photo under UV light

Electromagnetic Radiation (6) X-rays -- used in medicine. Ouch!

Electromagnetic Radiation (7) Gamma Rays-- some radioactive substances give it off • The last type of radiation is sometimes grouped with gamma rays… (8)Cosmic rays -- highest energy radiation; almost all of this radiation from the sun is blocked by the ozone layer and our atmosphere. Interesting superhero facts: • Superman has x-ray vision. • The Incredible Hulk was “created” by an accidental overdose of gamma radiation. • The Fantastic Four were “created” by cosmic rays.

Light is Characterized by its Wavelength and Frequency • Wavelength ( λ ) Frequency (n) is the number of times that light “waves” each second. – Measured in Hertz (Hz) also known as /sec. • Speed ( c ) is how wavelength and frequency are related.

c = The Speed of Light • λn (wavelength x frequency)= c • c = 3. 00 x 108 m/s (meters per second)

The Energy of Light is Related to its Frequency • E = hn, where – E = the energy of light – h = Planck's constant = 6. 626 x 10 -34 J/s – n = frequency (in Hz or /sec) For example, light with a frequency of 450 GHz has an energy of 3. 0 x 10 -22 J.

The Photoelectric Effect • Refers to the emission of electrons from a metal when light shines on the metal. • The wave theory of light predicted that any frequency of light could knock out an electron, but this proved to be untrue. • Only certain frequencies of light could supply enough energy to eject an electron.

Albert Einstein • Proposed electromagnetic radiation is can be viewed as a stream of “particles” called photons with the equation: • Ephoton = hv = hc/λ • What prompted this conclusion? • Photoelectric Effect ….

This Explains why Different Types of Light have Different Energies • Radio waves have much less energy than visible light, which in turn has much less energy than x-rays. • The different colors of visible light have different energies, too. – Blue light is much more energetic than red light.

The Modern Atom • Soon after Rutherford determined that the positive charge in an atom resided in the nucleus, scientists began putting together a new model of the atom. • The main discovery that got them thinking was the realization that the energy of light is quantized.

Quantum Theory • A quantum of energy is the minimum quantity of energy that can be lost or gained by an atom. • Each particle of light carries a quantum of energy, referred to by Albert Einstein as “photons”. • Photons are particles of electromagnetic radiation having zero mass and carrying a minimum quantity (a quantum) of energy.

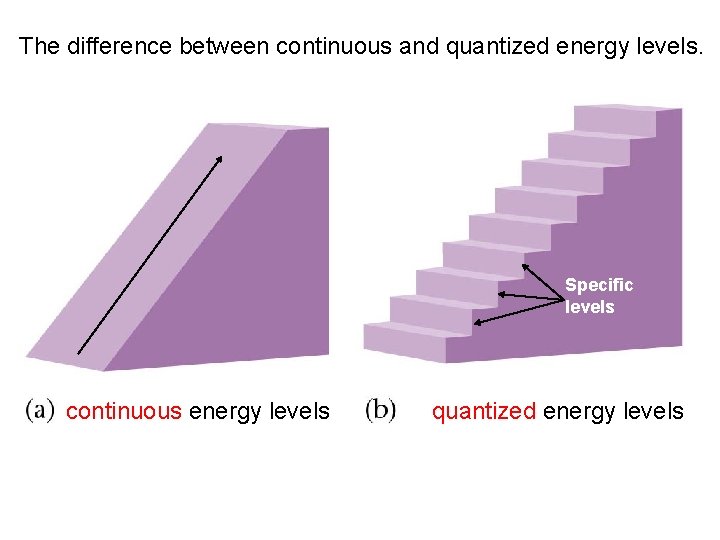
Light is Quantized • When something is quantized, it means it can exist only at certain points. • An example is an increase in altitude: if you walk up a ramp, you can stop and rest at any altitude you want. • If you walk up some stairs, you can only stop at the altitudes that correspond to the height of one of the stairs.

The difference between continuous and quantized energy levels. Specific levels continuous energy levels quantized energy levels

Max Planck / Albert Einstein “Dual Nature of Light” 1. Energy is quantized. It occurs in discrete units called quanta… it is NOT continuous. 2. Electromagnetic Radiation shows not only characteristics of a wave but also characteristics of a particles of matter. “Dual (Two) Nature of Light” …. . So actually how is light produced?

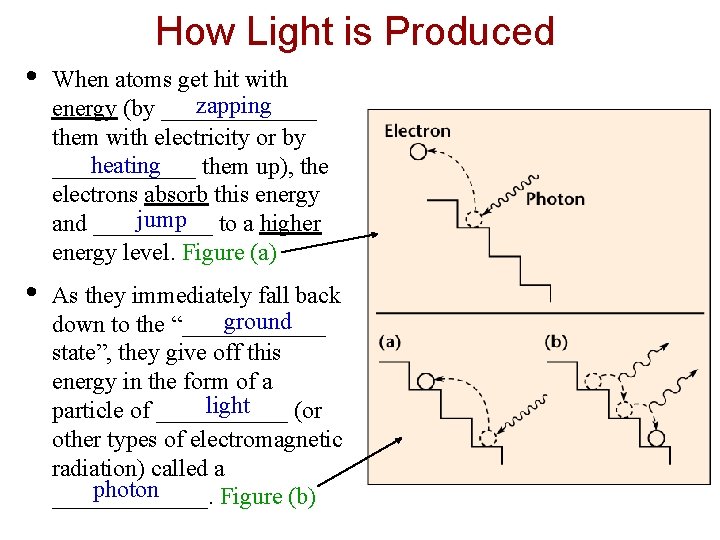
How Light is Produced • When atoms get hit with zapping energy (by _______ them with electricity or by heating ______ them up), the electrons absorb this energy jump to a higher and _____ energy level. Figure (a) • As they immediately fall back ground down to the “______ state”, they give off this energy in the form of a light particle of ______ (or other types of electromagnetic radiation) called a photon _______. Figure (b)

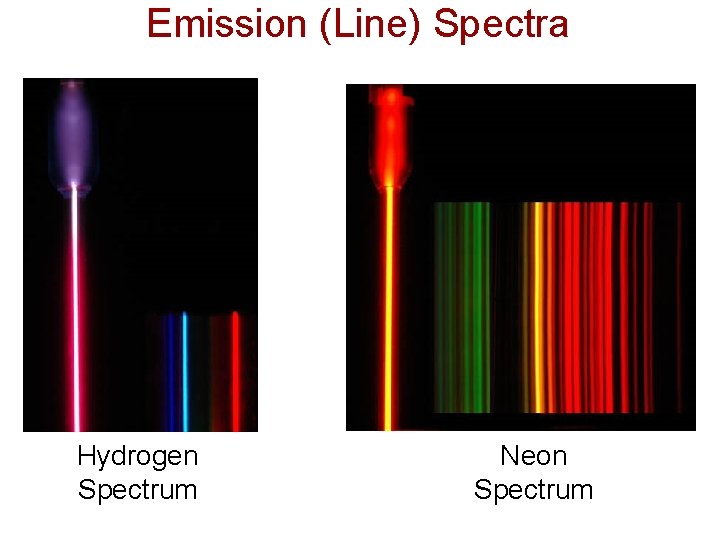
Spectroscopy • People began to notice that different elements gave off different colors of light when they are heated (called their spectra). • They had no idea why this happened, but they knew it was reproducible and could be used to tell one element from another. • This process is known as “spectroscopy”, and led to Bohr's model of the atom.

Bohr's Model of the Hydrogen Atom Bohr hypothesized the following: • The electrons in an atom circle the nucleus in circular orbitals. • The orbitals closest to the nucleus have the lowest amount of energy and the orbitals gain energy the further they get from the nucleus.

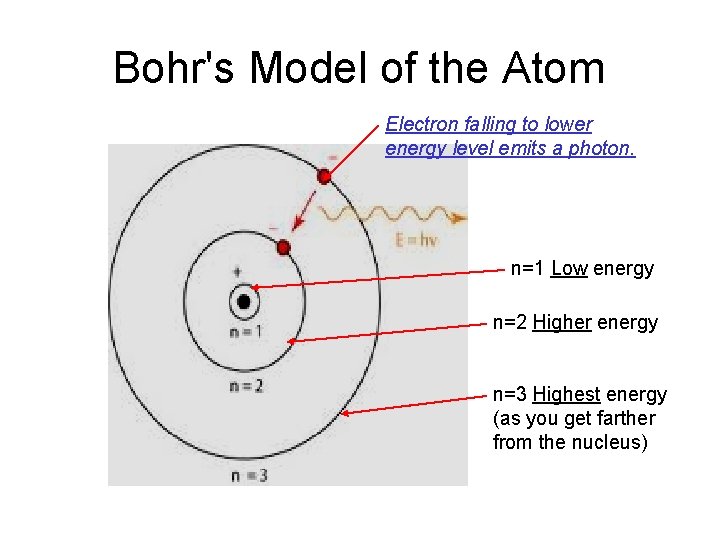
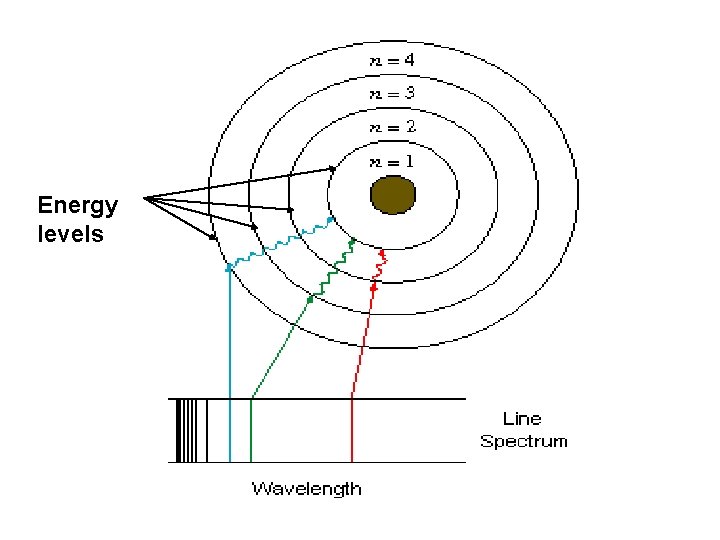
Bohr's Model of the Atom Electron falling to lower energy level emits a photon. n=1 Low energy n=2 Higher energy n=3 Highest energy (as you get farther from the nucleus)

How Does This Result in Different Colors of Light? • When an atom is at rest, each electron lies in its lowest possible energy state, its ground state. • When energy is added to an atom the electrons absorb it and jump up to a higher energy level. • After some time has passed, the electron falls back down to their original ground state orbitals, and emit a photon as they do.

Energy levels

There are Only So Many Orbitals • A limited number of orbitals means only certain energies of light can be given off by an atom. • Because the orbitals of all atoms have different energies, no two atomic spectra will ever be the same! • This is how astronomers can tell what planets and stars are made of from millions of light years away.

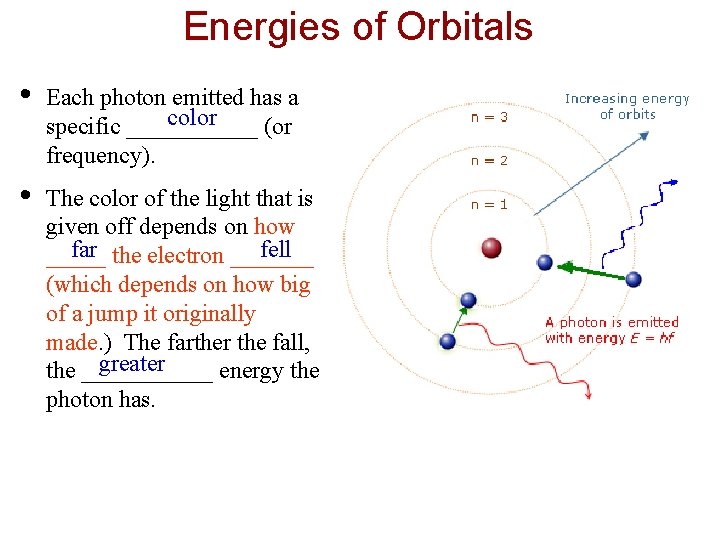
Energies of Orbitals • Each photon emitted has a color specific ______ (or frequency). • The color of the light that is given off depends on how far the electron _______ fell _____ (which depends on how big of a jump it originally made. ) The farther the fall, greater the ______ energy the photon has.

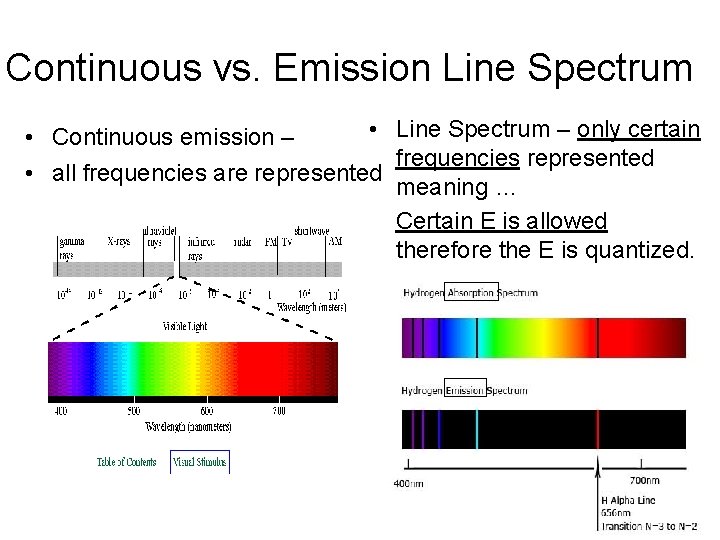
Continuous vs. Emission Line Spectrum • Line Spectrum – only certain • Continuous emission – frequencies represented • all frequencies are represented meaning … Certain E is allowed therefore the E is quantized.

Photons of Light in Bands of Color • • energy levels around Since electrons are located only in certain _____ color of light are emitted. the nucleus, only certain specific _____ spectroscope Scientists use a _________ to separate these colors into bar code of color bands of light. These bands of color look like a ______ which is characteristic of that element. No two elements produce the spectrum same _______ of colors. This can be used to distinguish one element from another contained in a sample. (See Fig. 13. 11)

Emission (Line) Spectra Hydrogen Spectrum Neon Spectrum

Neils Bohr's Hydrogen Model • Bohr first described e- as moving around nucleus in discrete orbits • His equation represents the energy levels available to e- in the hydrogen atom • Bohr's simple model, however, only worked for hydrogen and did not explain the spectra of atoms with more than one electron. • More research on electrons was to come. . .

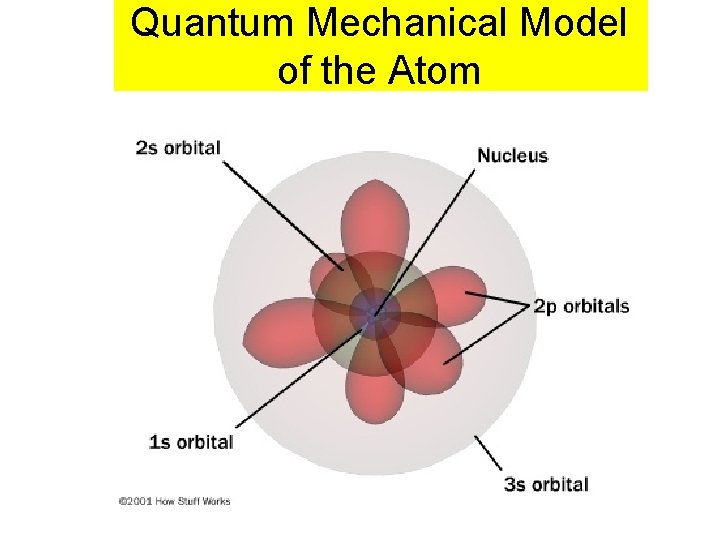
Quantum Mechanical Model of the Atom

Quantum Mechanical Model of the Atom

Quantum Numbers • Describe the locations of the e-’s around the nucleus. • Quantum #’s are sort of like a home address for the electron. • This information about the location of the e-’s in an atom can be used to: (1) determine chemical & physical properties for the elements. (2) show the Periodic Table is organized. (3) show and why elements combine to form compounds.

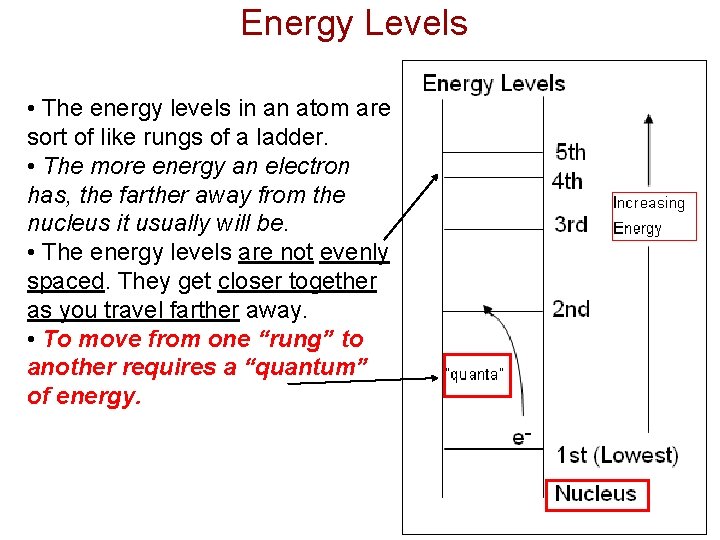
Energy Levels • The energy levels in an atom are sort of like rungs of a ladder. • The more energy an electron has, the farther away from the nucleus it usually will be. • The energy levels are not evenly spaced. They get closer together as you travel farther away. • To move from one “rung” to another requires a “quantum” of energy.

The Four Quantum Numbers 1. Principal Q. #: Describes the distance that the electron is from the nucleus. The bigger the number, the farther away the electron is. Example: (1=closest, 2, 3, 4. . . farther away) 1 2 3 nucleus

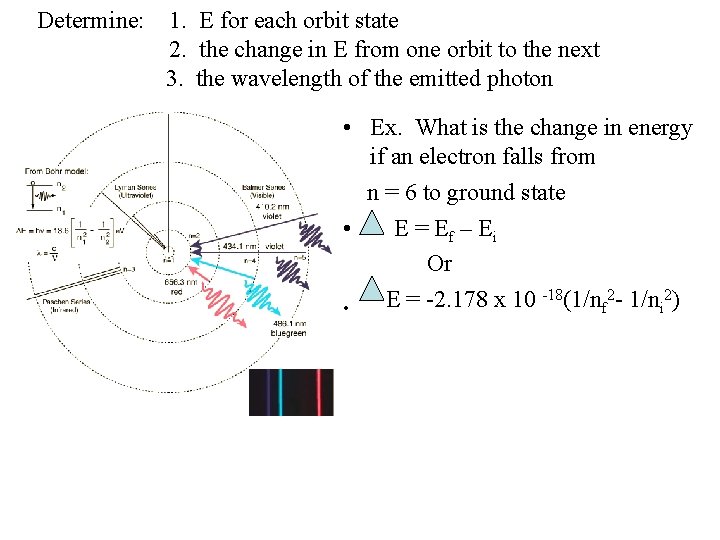
Determine: 1. E for each orbit state 2. the change in E from one orbit to the next 3. the wavelength of the emitted photon • Ex. What is the change in energy if an electron falls from n = 6 to ground state • E = E f – Ei Or -18(1/n 2 - 1/n 2) E = -2. 178 x 10 f i •

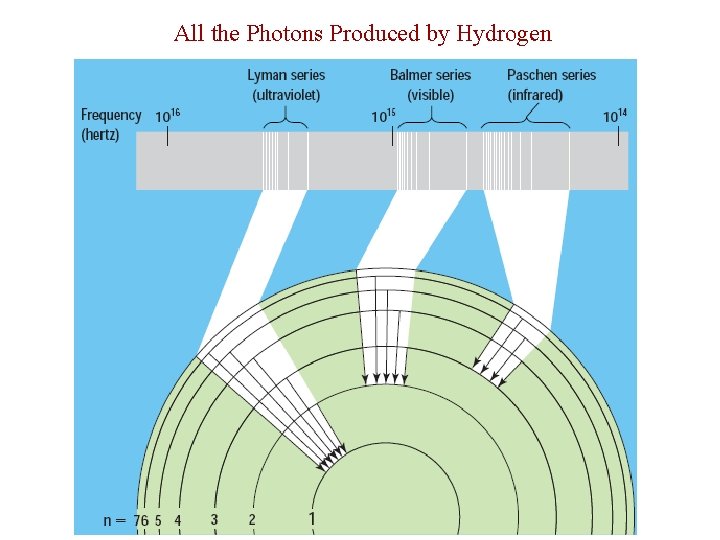
All the Photons Produced by Hydrogen

Since light (wave) can act as a particle, can a particle( like an electron) act as a wave ? • Louis De. Broglie • Waves confined to a certain space have certain frequencies, so could electrons confined to a certain space be considered waves? λ = h/mv : where v is the velocity and m is the mass.

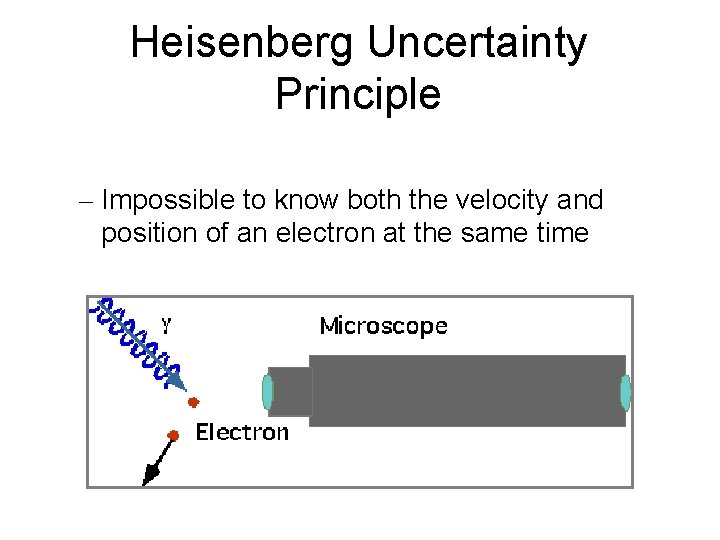
Heisenberg Uncertainty Principle – Impossible to know both the velocity and position of an electron at the same time

Schrödinger Wave Equation (1926) finite # of solutions ⇒ quantized energy levels – defines probability of finding an e-

Schrodinger's Electron Cloud • Orbital (“electron cloud”) – A 3 -dimensional region in space where there is 90% probability of finding an e-

• E = hv : where v is frequency in hertz (sec-1) E is energy in joules h is Plank’s constant h = ( 6. 626 x 10 -34 J s ) • Theorized energy is not continuous but is quantized in discrete units or packets called QUANTA.

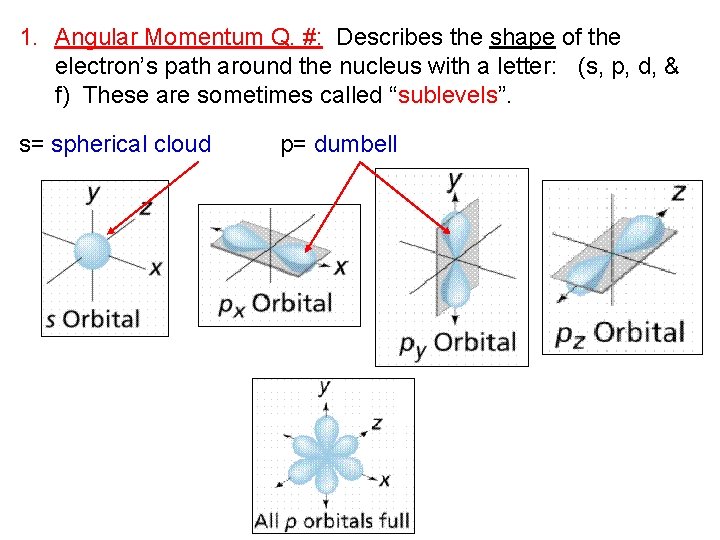
1. Angular Momentum Q. #: Describes the shape of the electron’s path around the nucleus with a letter: (s, p, d, & f) These are sometimes called “sublevels”. s= spherical cloud p= dumbell

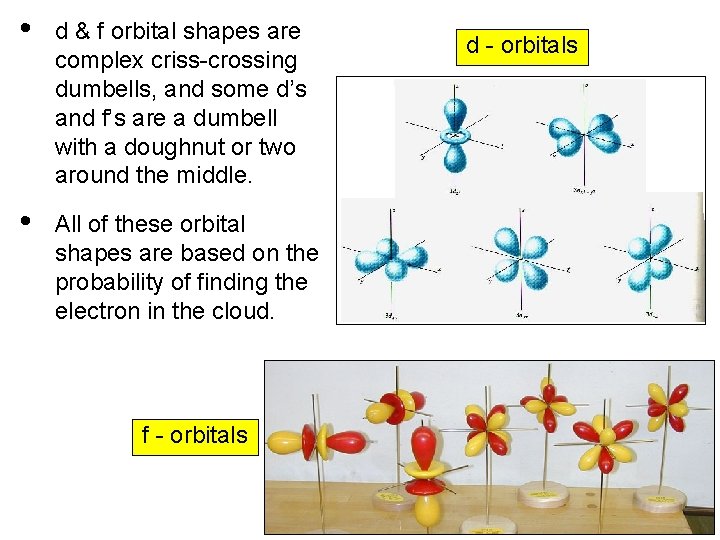
• d & f orbital shapes are complex criss-crossing dumbells, and some d’s and f’s are a dumbell with a doughnut or two around the middle. • All of these orbital shapes are based on the probability of finding the electron in the cloud. f - orbitals d - orbitals

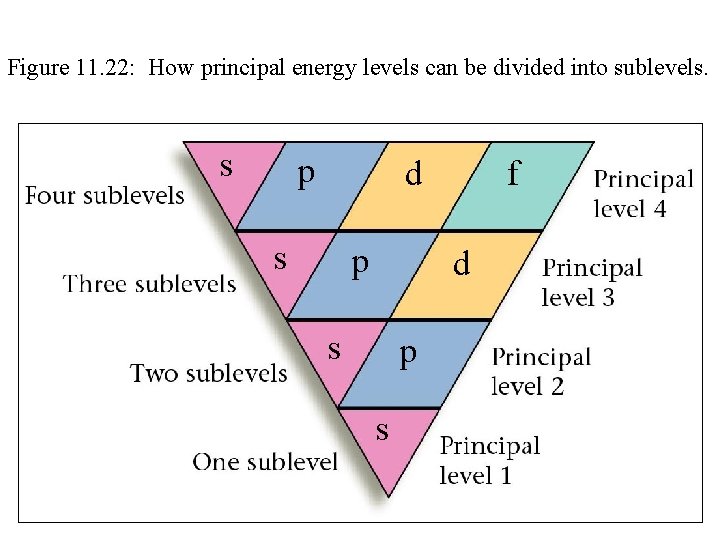
Figure 11. 22: How principal energy levels can be divided into sublevels. s p d s p f d s p s

• Magnetic Q. #: tells how many orientations in 3 -D there about the nucleus for each orbital shape. 3 1 s=___ orientation p= ___ orientations. . . (x, y, and z) 5 d= ___ orientations • 7 f= ___ orientations The orientations are represented with a line or a box. Examples: ___ This means a spherical orbital at a distance of 1 s “ 1” (close) to the nucleus. This orbital is centered about the x, y, and z axis. □□□ This represents an ellipsoid orbital with its 4 p 3 possible orientations at a distance of “ 4 ”from the nucleus.

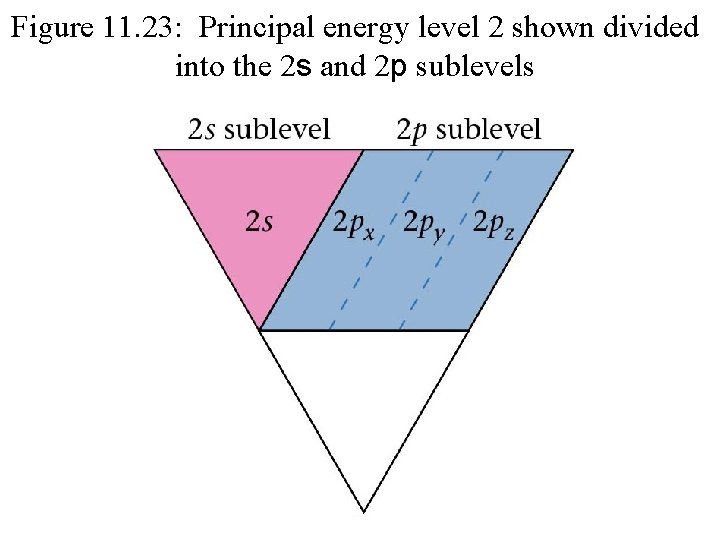
Figure 11. 23: Principal energy level 2 shown divided into the 2 s and 2 p sublevels

Compare the wavelength for an electron (mass = 9. 11 x 10 -31 kg) traveling at a speed of 1. 0 x 107 m/s with that of a ball (mass = 0. 10 kg) traveling at 35 m/s. • Remember 1 joule = 1 kg m 2/s 2 ; and λ = h/mv therefore 6. 626 x 10 -34 Js = 6. 626 x 10 -34 kg m 2/s λ e- = 6. 626 x 10 -34 kg m 2/s = 7. 27 x 10 -11 m (9. 11 x 10 -31 kg)(1. 0 x 107 m/s) λ ball = 6. 626 x 10 -34 kg m 2/s = 1. 9 x 10 -34 m (0. 10 kg)(35 m/s) ***** the ball has an extremely small wavelength one that our eye could not possibly pick up.

• • Spin Q. #: describes how the electron in an orientation is spinning around the nucleus. Some like to imagine it spinning “clockwise” and “counterclockwise”. The spin is represented as an arrow in the direction of the spin. Example: ↑ This represents one electron in a spherical 2 s orbital with spin “ up or +1/2” at a distance of “ 2” from the nucleus. • Remember, the four quantum numbers tell us the location, or “address” of each electron in an atom. • This information is vital in understanding the layout of the Periodic Table and the reasoning behind why and how atoms form bonds.

Electron Configurations • Electron configurations are notations that represent the four Quantum #’s for all of the electrons in a particular atom. Here are the rules for these notations: • Rule #1 (Aufbau Principle): Electrons fill lowest energy orbitals first. Examples: 1 s would be filled before 2 s 3 s would fill before 3 p

• Rule #2: Only 2 electrons can fit into each orientation. ↓ ↑ Example: ↑___ 1 s 2 s • Rule #3 (Pauli Exclusion Principle): Electrons in the same orientation have opposite spin. Example: • ↑↑ not ↓____ 1 s ↑↓ ↑↑ ___ not ___ 1 s 1 s □ Rule #4 (Hund’s Rule): “Monopoly rule”---> Every “ ” in an orbital shape gets an electron before any orientation gets a second e -. Example: □□□ ↑ ↑ 2 p ↑ not □□□ ↓↑ 2 p ↑

• Rule #5: The Exceptions – – Half-filled or completely filled d & f sublevels have lower energies and are more stable than partially filled d’s and f’s. This means that an atom can “borrow” one of its “s” electrons from the previous orbital to become more stable. Example: ___ ↑ ↓ ___ 5 s ___ ___ 5 s – ↑ ↓ ___ ↑↓ ___↑ ↓ ___ ↑ 4 d ↑↓ ↑↓ becomes ↑↓ ↑↓ ___ ↑↓ ↑ ___ 4 d Because the 4 d sublevel is now full, the atom is at a lower energy state and therefore more stable.

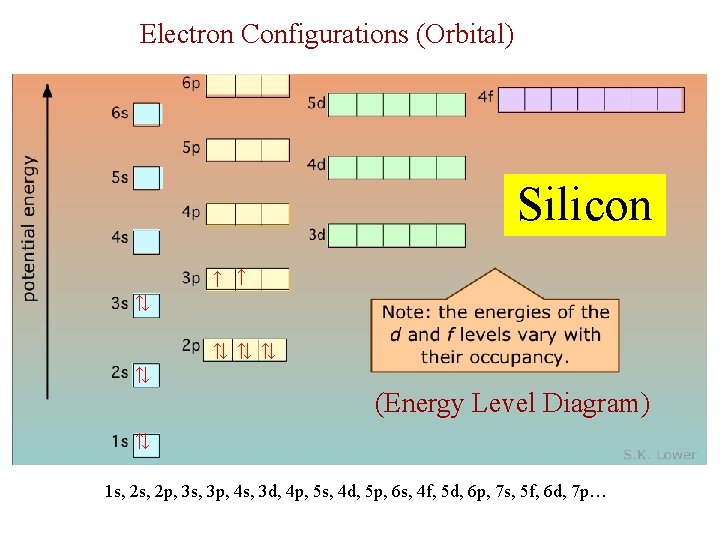
Electron Configurations (Orbital) Silicon ↑ ↑ ↑↓ ↑↓ ↑↓ (Energy Level Diagram) ↑↓ 1 s, 2 p, 3 s, 3 p, 4 s, 3 d, 4 p, 5 s, 4 d, 5 p, 6 s, 4 f, 5 d, 6 p, 7 s, 5 f, 6 d, 7 p…

Electron Configurations Practice Problems: Write the electron configuration notation for each of the following atoms: • Hydrogen • Carbon • Iron • Bromine Shorthand Method: Assumes we already know about the # of • H • C • Fe • Br □.

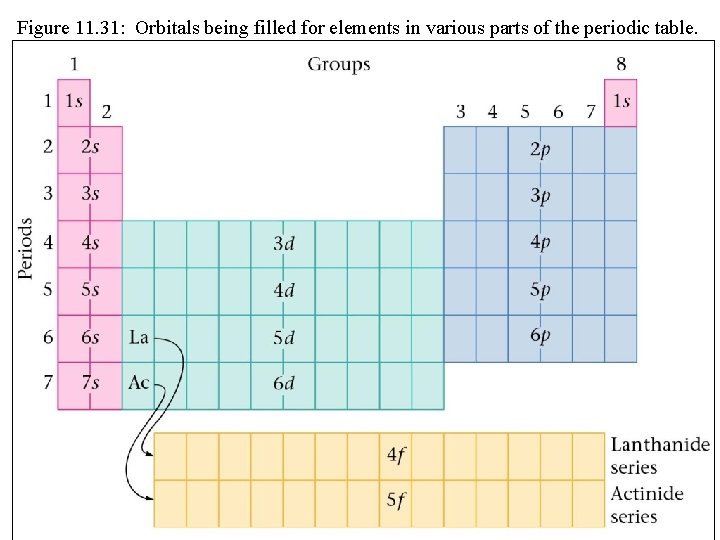
Figure 11. 31: Orbitals being filled for elements in various parts of the periodic table.

Electron Configurations & Properties • How do electron configurations relate to the chemical and physical properties of an element? • All elements with the same outer shell e- configurations have the similar properties. • This means that elements in the same vertical group have similar properties.

More Practice Problems Bromine (1) Which element has its last electron as a 4 p 5? ______ F, Cl, I, At (2) Which elements are similar in properties as Bromine? _____ (3) What would the outer shell electron configuration look like for the element underneath Radon, (Rn)? … 7 s 2 5 f 14 6 d 10 7 p 6 1 4 f 2 (4) Which electron is added after 6 s ? ____ (5) Which element would “borrow” a 5 s electron to get a half-filled Mo “d” sublevel? ______ (6) What is the shape of the last orbital filled in Calcium, (Ca)? sphere _____ 4 (7) How many electrons are in the last “p-orbital” of Sulfur, (S)? ____

Feeling overwhelmed?