Discovering Knowledge from Medical Databases Using Evolutionary Algorithms

Discovering Knowledge from Medical Databases Using Evolutionary Algorithms Man Leung Wong, Wai Lam, Kwong Sak Leung, Po Shun Ngan, Jack C. Y. Cheng Department of Information Systems, Lingnan University, Hong Kong Advisor: Dr. Hsu Reporter: M. H. Lin 2020/10/26 1

Outline n n n n n Motivation Objective Evolutionary Algorithm Primer The Learning Tasks Rule Learning Using Generic Genetic Programming Learning Bayesian Networks from Discrete Variables Learning Results Conclusions Personal Opinion 2020/10/26 2

Motivation n The increasing use of computers results in an explosion of information. Data can be best used if the knowledge hidden can be uncovered. With computerization in hospitals, a huge amount of data has been collected. It is beneficial if these data can be analyzed automatically. KDD: the nontrivial process of identifying valid, novel, potentially useful, and ultimately understandable patterns in data. n 2020/10/26 selection→ preprocessing →transformation →data mining algorithm →interpreted and evaluated 3

Objective n n Introduce our approaches ( Evolutionary Algorithms ) for discovering knowledge from two specific medical databases. Two different representations of knowledge are learned n n 2020/10/26 Rules: capture interesting patterns and regularities in the database. Casual structures: represented by Bayesian networks capture the causality relationships among the attributes. 4

Evolutionary Algorithm Primer n n Evolutionary algorithms simulate natural evolution ( Darwinian principle ) to perform function optimization and machine learning. Evolutionary Algorithms contain genetic algorithms, genetic programming, evolutionary programming and evolution strategies. 2020/10/26 5

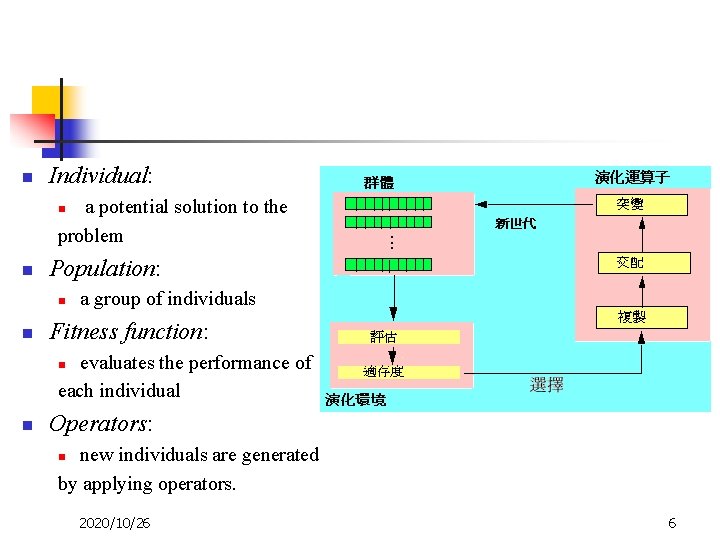
n Individual: a potential solution to the problem n n Population: n n a group of individuals Fitness function: evaluates the performance of each individual n n Operators: new individuals are generated by applying operators. n 2020/10/26 6

The Learning Tasks n n n Medical Databases Rule Learning Bayesian Network Learning 2020/10/26 7

Medical Databases n Two medical databases from the Orthopaedic Department of the Prince of Wales Hospital of Hong Kong. n Fracture database n n n Scoliosis database n n 2020/10/26 6500 records of children (0~16)with limb fractures Between year 1984~1996 500 records Scoliosis Classification (K-I, K-III, K-IV, K-V, TL, L) 8

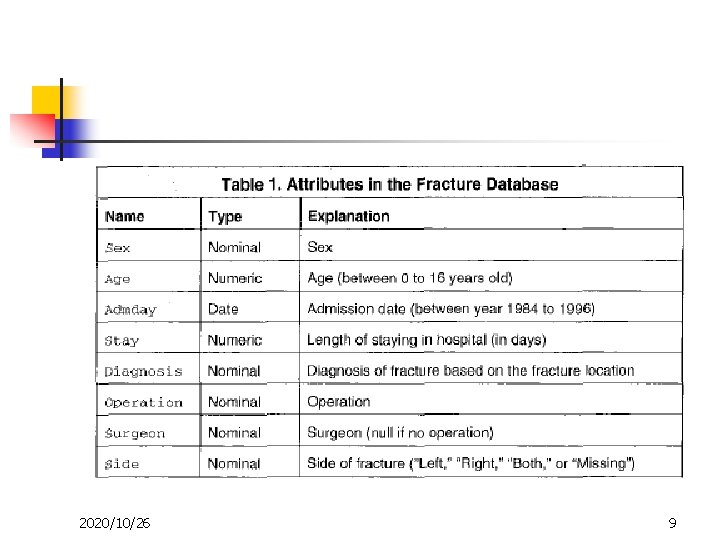
2020/10/26 9

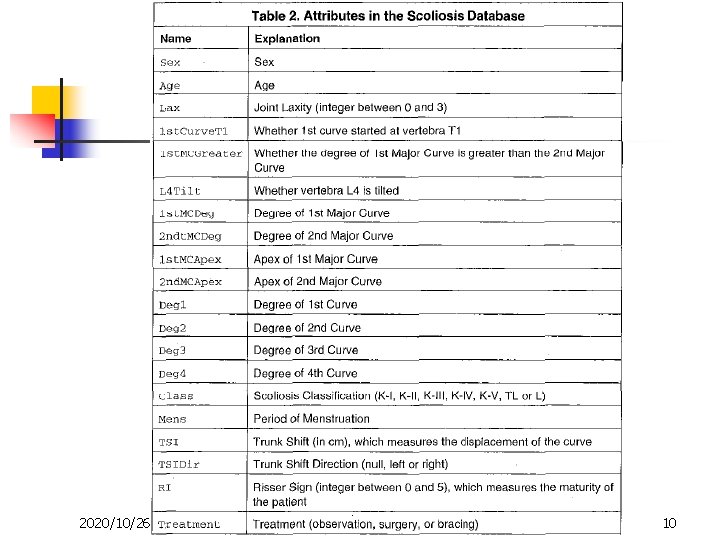
2020/10/26 10

Rule Learning n n n A rule is a sentence of the form “if antecedents, then consequent. ” the antecedent part is a conjunction of descriptions about attributes, while the consequent is a descriptor for a single attribute The accuracy or the confidence of a rule is the probability that the consequent occurs under the condition that the antecedents occur. If attr 1=0 and attr 2 between 100 and 150 and attr 3≠ 50, then attr 4=T Confidence: 39. 75%; Support: 8. 42%; Probability of consequent: 23. 43% 2020/10/26 11

Bayesian Network Learning n n n A Bayesian network is a different model used to represent probabilistic knowledge of data. It captures the conditional probabilities between variables and focuses on causality relationships among variables. Formally, a Bayesian network is a directed acyclic graph (DAG). 2020/10/26 12

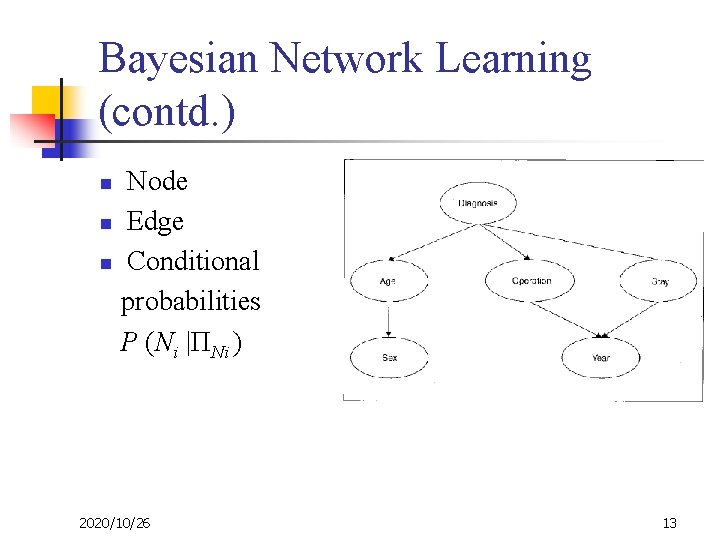
Bayesian Network Learning (contd. ) Node n Edge n Conditional probabilities P (Ni |ΠNi ) n 2020/10/26 13

Rule Learning Using Generic Genetic Programming n n GGP is an extension of genetic programming, which uses a grammar to control the structures being searched. Grammar n n n 2020/10/26 A grammar is provided by the user as a template for rules A set of rules is derived by using this grammar to form the initial population. The grammar specifies that a rule is of the form “if antecedents then consequent. ” 14

2020/10/26 15

The Loop of GGP n n In each generation, individuals are selected stochastically to evolve offspring by the three genetic operators. Crossover produces one child from two parents. Mutation is an asexual operation. A part in the parental rule is selected and replaced by a randomly generated part. The dropping condition is used to generalize rules. 2020/10/26 16

Evaluation of Rules n n An evaluation function based on the supportconfidence framework is developed as the fitness function. Support measures the coverage of a rule. n n |A&B| Confidence factor (cf) is the confidence of the consequent to be true under the condition that the antecedents are also true. n 2020/10/26 |A&B| / |A| 17

Evaluation of Rules (contd. ) n n n When evaluating the confidence of a rule, we need to consider the average probability of consequent ( prob = |B|/N ) cf_part = cf * log( ) Fitness function is defined as: If support < min_support then raw_fitness = support Else raw_fitness = w 1 * support + w 2 * cf_part 2020/10/26 18

Token Competition n n Assume each record in the training set can provide a resource, called a token. If a rule can match a record, it sets a flag to indicate the token is seized. Other weaker rules can not get the token. A rule with a high score on raw_fitness can exploit the niche by seizing as many tokens as it can. The modified fitness is defined as: modified_fitness = raw_fitness * count / ideal count is the number of tokens that the rule actually seized, and ideal is the total number of tokens that it can seize. 2020/10/26 19

End of the Loop n n One-half of the individuals with the higher fitness scores after token competition are retained and passed to the next generation. The whole process iterates until maximum number of generations has been reached. 2020/10/26 20

Learning Bayesian Networks from Discrete Variables n n MDLEP is based on evolutionary programming (EP) and the minimum description length (MDL) The MDL metric is defined to measure the total description length, DL, of a network structure G. The total description length of a network is the sum of description lengths of each node. The length of each node is defined based on two components n n 2020/10/26 The network description length : simplicity The data description length : accuracy 21

The Loop of MDLEP n n n A set of DAGs is randomly created to make up the initial population. Each DAG produces a child by performing a number of mutations. Each DAG is evaluated by the MDL metric. One-half of DAGs with the highest tournament scores are retained for the next generation. The process is repeated until the maximum number of generations is reached. The network with the lowest MDL score is output as the result. 2020/10/26 22

Discretizing Continuous Variables while Learning Bayesian Networks n n n A Bayesian network can only represent discrete variables. One approach to handle databases with continuous variables is to descretize them first. Different discretization policies will produce different network structures. 2020/10/26 23

Discretization Policy n n A discretization sequence, λ, defines a function that maps a continuous variable to a discrete variable. A discretization policy, Λ={λi : Xi is continuous }, is a collection of descretization sequences for each continuous variable. This policy defines a new set of variables, U* = {X 1*, …, Xn*}, where Xi* = fλ(Xi) if Xi is continuous and Xi* = Xi otherwise. Friedman and Goldszmidt extend the MDL score to evaluate the discretization policy while learning Bayesian network structures. 2020/10/26 24

Learning Discretization Policy Using Genetic Algorithms n n It starts with an initial discretization policy MDLEP is then used to learn the best network structure. Based on this structure, a GA is used to learn the best discretization policy. The process is iterated until the maximum number of iterations is reached. 2020/10/26 25

Individual Representation n n One bit string to represent one discretization sequence Each individual represent a possible discretization policy 2020/10/26 26

Genetic Operators n n Reproduction: Crossover: Mutation: Shift: this operator changes the threshold value in the discretization sequence to the next or previous midpoint value. 01001 2020/10/26 shift 010010101 27

Results of Bayesian Network Learning－Fracture Database 2020/10/26 28

Results of Rule Learning－ Fracture Database 2020/10/26 29

2020/10/26 30

Results of Bayesian Network Learning－Scoliosis Database 2020/10/26 31

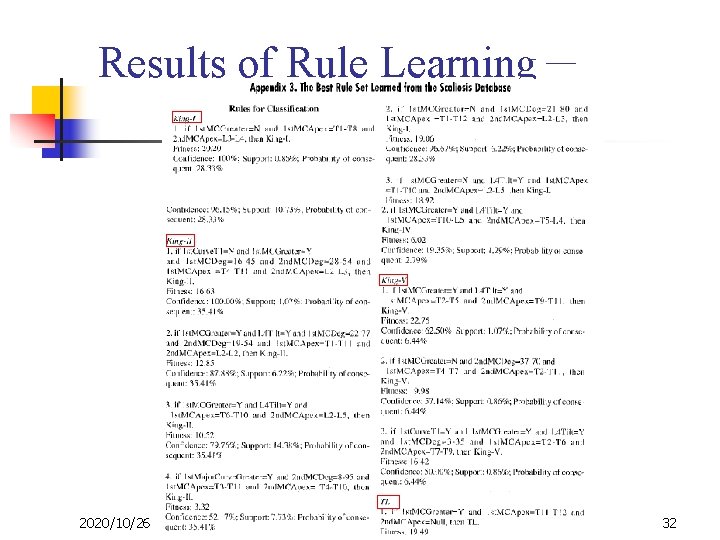
Results of Rule Learning－ 2020/10/26 32

2020/10/26 33

Conclusion n We have presented our approach for knowledge discovery from two specific medical databases n n n Two different representations of knowledge are learned n n n From the fracture database, we discovered knowledge about the patterns of child fractures From the scoliosis database, we discovered knowledge about the classification of scoliosis. Rule learning : capture interesting patterns of the data. Casual structures: first, a discretization policy is learned , and then Bayesian networks are induced. Then result demonstrate that the knowledge discovery process can find interesting knowledge about the data. 2020/10/26 34

Personal Opinion n What applications of EAs are there? n n n n n 2020/10/26 Artificial Life Bioinformatics: protein folding, RNA folding, sequence alignment Cellular Programming Evolvable Hardware : evolware, bioware Game Playing Job-Shop Scheduling Management Sciences Non-linear Filtering Timetabling 35