Discovering Clusters in Graphs CS 246 Mining Massive

Discovering Clusters in Graphs CS 246: Mining Massive Datasets Jure Leskovec, Stanford University http: //cs 246. stanford. edu

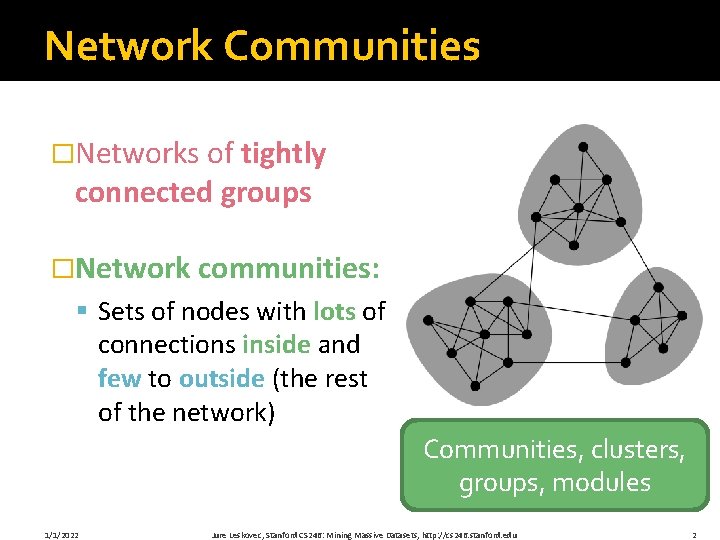
Network Communities �Networks of tightly connected groups �Network communities: § Sets of nodes with lots of connections inside and few to outside (the rest of the network) Communities, clusters, groups, modules 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 2

Finding Network Communities �How to automatically find such densely connected groups of nodes? �Ideally such clusters then correspond to real groups �For example: 1/1/2022 Communities, clusters, groups, modules Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 3

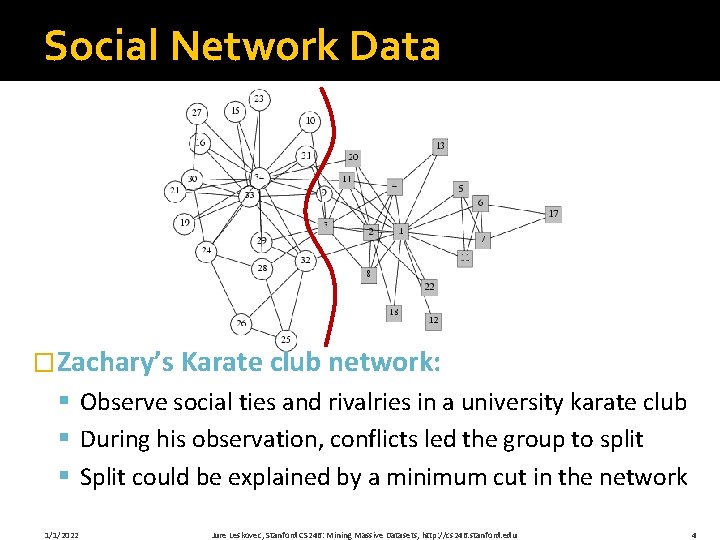
Social Network Data �Zachary’s Karate club network: § Observe social ties and rivalries in a university karate club § During his observation, conflicts led the group to split § Split could be explained by a minimum cut in the network 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 4

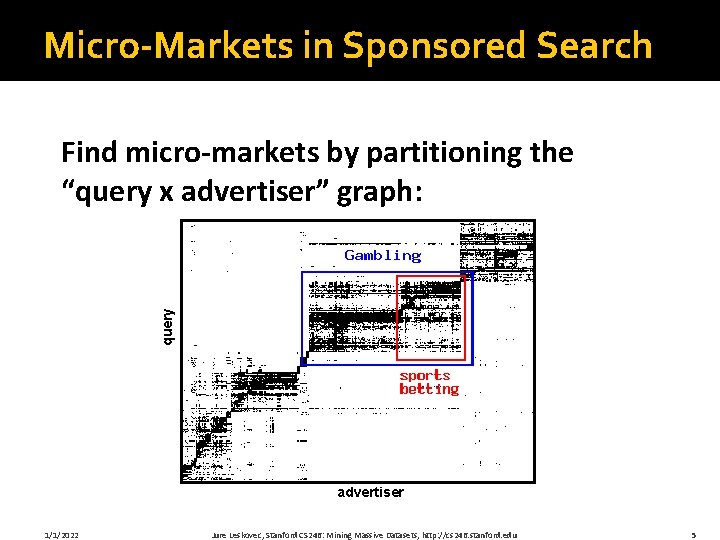
Micro-Markets in Sponsored Search query Find micro-markets by partitioning the “query x advertiser” graph: advertiser 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 5

Method No. 1: Trawling Directed graphs (unweighted edges)

[Kumar et al. ‘ 99] Trawling �Searching for small communities in … … … the Web graph �What is the signature of a community / discussion in a Web graph? Use this to define “topics”: What the same people on the left talk about on the right Remember HITS! Dense 2 -layer graph Intuition: Many people all talking about the same things 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 7

Searching for Small Communities �A more well-defined problem: Enumerate complete bipartite subgraphs Ks, t § Where Ks, t : s nodes on the “left” where each links to the same t other nodes on the “right” X K 3, 4 Y |X| = s = 3 |Y| = t = 4 Fully connected 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 8

The Plan: (1), (2) and (3) [Kumar et al. ‘ 99] �Two points: § (1) Dense bipartite graph: the signature of a community/discussion § (2) Complete bipartite subgraph Ks, t § Ks, t = graph on s nodes, each links to the same t other nodes �Plan: § (A) From (2) get back to (1): § Via: Any dense enough graph contains a smaller Ks, t as a subgraph § (B) How do we solve (2) in a giant graph? § What similar problems were solved on big non-graph data? § (3) Frequent itemset enumeration 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 9

[Agrawal-Srikant ‘ 99] Frequent Itemset Enumeration �Marketbasket analysis. Setting: § Market: Universe U of n items § Baskets: m subsets of U: S 1, S 2, …, Sm U (Si is a set of items one person bought) § Support: Frequency threshold f �Goal: § Find all subsets T s. t. T Si of f sets Si (items in T were bought together at least f times) �What’s the connection between the itemsets and complete bipartite graphs? 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 10

[Kumar et al. ‘ 99] From Itemsets to Bipartite Ks, t Say we find a frequent itemset Y={a, b, c} of supp. s So, there are s nodes that link to all of {a, b, c}: View each node i as a set Si of nodes i points to a i b c d x Si={a, b, c, d} Find frequent itemsets: s … minimum support t … itemset size We found Ks, t! Ks, t = a set Y of size t that occurs in s sets Si 1/1/2022 a a b b c y a z c b c x y X z Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu a b c Y 11

[Kumar et al. ‘ 99] From Itemsets to Bipartite Ks, t �Itemsets finds Complete bipartite graphs! a �How? § View each node i as a set Si of nodes i points to § Ks, t = a set Y of size t that occurs in s sets Si § Looking for Ks, t set of frequency threshold to s and look at layer t – all frequent sets of size t 1/1/2022 b i c Si={a, b, c, d} d j i k X a b c d Y s … minimum support (|X|=s) t … itemset size (|Y|=t) Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 12

From Ks, t to Communities � 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 13

Proof: Ks, t and Communities f(x) � x 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 14

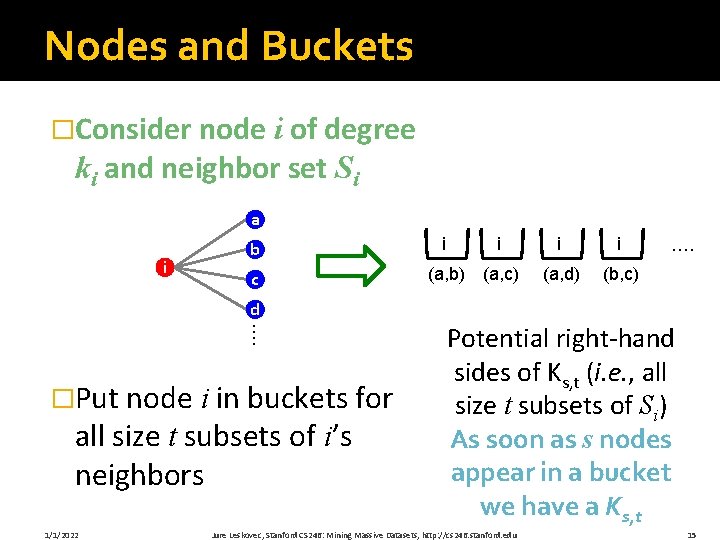
Nodes and Buckets �Consider node i of degree ki and neighbor set Si a i b i i c (a, b) (a, c) (a, d) (b, c) …. d …. �Put node i in buckets for all size t subsets of i’s neighbors 1/1/2022 Potential right-hand sides of Ks, t (i. e. , all size t subsets of Si) As soon as s nodes appear in a bucket we have a Ks, t Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 15

Nodes and Buckets � = # of ways to select t elements out of ki (ki … degree of node i) By convexity (and ki > t) 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 16

Nodes and Buckets � Plug in: 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 17

And We are Done! �We have: Total height of all buckets: �How many buckets are there? �What is the average height of buckets? So, avg. bucket height s � By pigeonhole principle, there must be at least one bucket with more than s nodes in it � We found a Ks, t 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 18

Trawling — Summary [Kumar et al. ‘ 99] �Analytical result: § Complete bipartite subgraphs Ks, t are embedded in larger dense enough graphs (i. e. , the communities) § Biparite subgraphs act as “signatures” of communities �Algorithmic result: § Frequent itemset extraction and dynamic programming finds graphs Ks, t § Method is super scalable 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 19

Method #2: Spectral Graph Partitioning Undirected graphs (but can be have (non-negative) weighted edges)

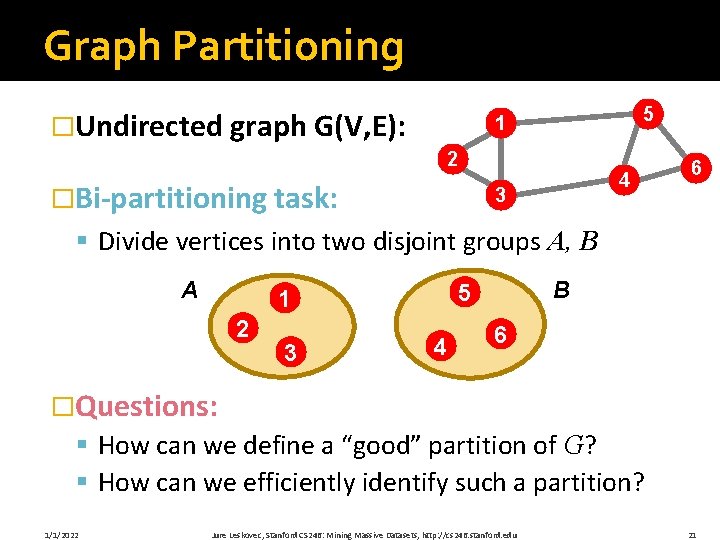
Graph Partitioning �Undirected graph G(V, E): 5 1 2 �Bi-partitioning task: 4 3 6 § Divide vertices into two disjoint groups A, B A 2 3 B 5 1 4 6 �Questions: § How can we define a “good” partition of G? § How can we efficiently identify such a partition? 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 21

Graph Partitioning �What makes a good partition? § Maximize the number of within-group connections § Minimize the number of between-group connections 5 1 2 3 A 1/1/2022 6 4 B Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 22

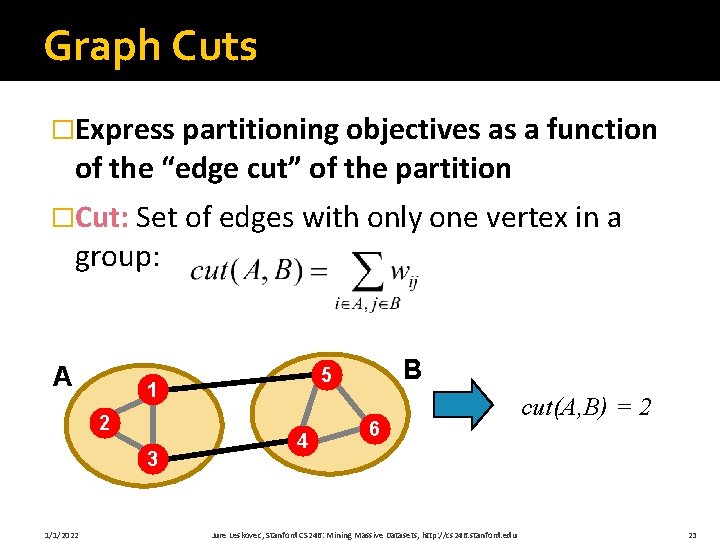
Graph Cuts �Express partitioning objectives as a function of the “edge cut” of the partition �Cut: Set of edges with only one vertex in a group: A 1 2 3 1/1/2022 B 5 4 6 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu cut(A, B) = 2 23

Graph Cut Criterion �Criterion: Minimum-cut § Minimise weight of connections between groups min. A, B cut(A, B) �Degenerate case: “Optimal cut” Minimum cut �Problem: § Only considers external cluster connections § Does not consider internal cluster connectivity 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 24

Graph Cut Criteria [Shi-Malik] � ki … degree of node i 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 25

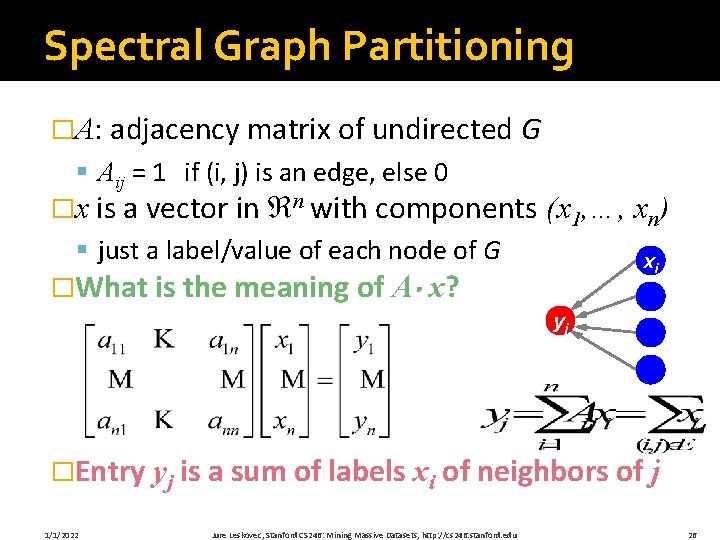
Spectral Graph Partitioning �A: adjacency matrix of undirected G § Aij = 1 if (i, j) is an edge, else 0 �x is a vector in n with components (x 1, …, xn) § just a label/value of each node of G �What is the meaning of A xi x? yj �Entry yj is a sum of labels xi of neighbors of j 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 26

What is the meaning of A·x? �jth coordinate of Ax: § Sum of the x-values of neighbors of j § Make this a new value at node j �Spectral Graph Theory: § Analyze the “spectrum” of matrix representing G § Spectrum: Eigenvectors of a graph, ordered by the magnitude (strength) of their corresponding eigenvalues: Note: We order i in increasing order 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 27

Example: d-regular Graph � 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 28

Example: Graph on 2 Components � A 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu B 29

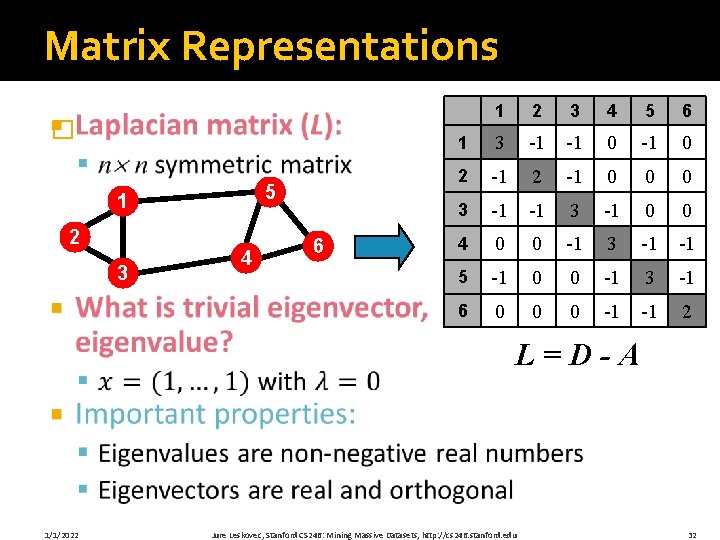
Matrix Representations �Adjacency matrix (A): § n n matrix § A=[aij], aij=1 if edge between node i and j 5 1 2 3 4 6 �Important properties: 1 2 3 4 5 6 1 0 1 0 2 1 0 0 0 3 1 1 0 0 4 0 0 1 1 5 1 0 0 1 6 0 0 0 1 1 0 § Symmetric matrix § Eigenvectors are real and orthogonal 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 30

Matrix Representations �Degree matrix (D): § n n diagonal matrix § D=[dii], dii = degree of node i 5 1 2 3 1/1/2022 4 6 1 2 3 4 5 6 1 3 0 0 0 2 0 0 3 0 0 0 4 0 0 0 3 0 0 5 0 0 3 0 6 0 0 0 2 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 31

Matrix Representations � 5 1 2 3 4 6 1 2 3 4 5 6 1 3 -1 -1 0 2 -1 0 0 0 3 -1 -1 3 -1 0 0 4 0 0 -1 3 -1 -1 5 -1 0 0 -1 3 -1 6 0 0 0 -1 -1 2 L=D-A 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 32

Overview �Here is what we will do next: �We just saw that L has eigenvalue 0 and eigenvector (1, …, 1) �Now the question is, what is lambda 2 doing? § We will see that eigenvector that corresponds to lambda 2 really does community detection § It tries to separate nodes on the left and on the right of zero so that the minimum number of edges points across zero § Give a picture of the embedding and how it has to sum to zero and have unit lenght 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 33

Say that really each eigne pairs is a solution to the above equestion: -- I want smallest possible eigenvalue and a vector that is orthogonal to everty other one and has length 1 λ 2 as an Optimization Problem � xi xj Think of xi as a numeric value of node i Then we want so set values xi such that they don’t differ across the edges 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 34

λ 2 as an Optimization Problem � All labelings of nodes so that i xi = 0 5 1 2 3 1/1/2022 4 6 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 35

λ 2 as an Optimization Problem � 5 1 2 3 4 6 A 1/1/2022 B Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 36

λ 2 as an Optimization Problem 0 � 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 38

Finding the Optimal Cut � A B Looks like our equation for 2! 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 39

Optimal Cut and λ 2 � To learn more: A Tutorial on Spectral Clustering by U. von Luxburg 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 40

So far… How to define a “good” partition of a graph? � § Minimize a given graph cut criterion � How to efficiently identify such a partition? § Approximate using information provided by the eigenvalues and eigenvectors of a graph � 1/1/2022 Spectral Clustering Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 41

Spectral Clustering Algorithms Three basic stages: 1. Pre-processing § Construct a matrix representation of the graph 2. Decomposition § § Compute eigenvalues and eigenvectors of the matrix Map each point to a lower-dimensional representation based on one or more eigenvectors 3. Grouping § 1/1/2022 Assign points to two or more clusters, based on the new representation Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 42

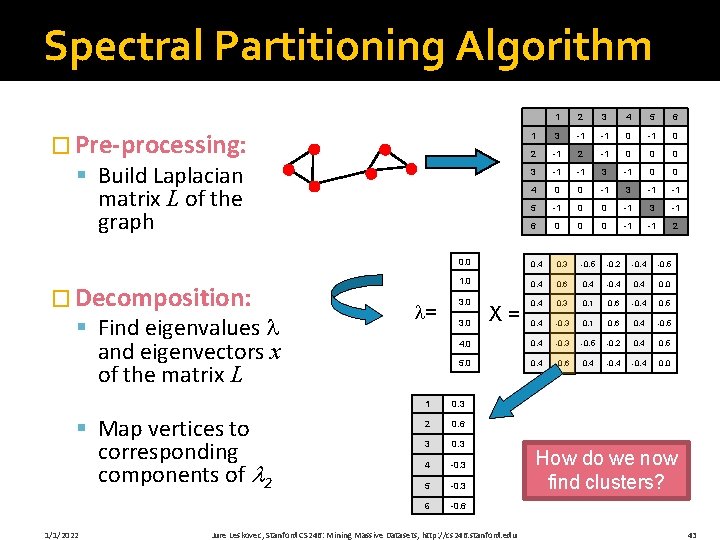
Spectral Partitioning Algorithm 1 2 3 4 5 6 1 3 -1 -1 0 2 -1 0 0 0 3 -1 -1 3 -1 0 0 4 0 0 -1 3 -1 -1 5 -1 0 0 -1 3 -1 6 0 0 0 -1 -1 2 0. 0 0. 4 0. 3 -0. 5 -0. 2 -0. 4 -0. 5 1. 0 0. 4 0. 6 0. 4 -0. 4 0. 0 3. 0 0. 4 0. 3 0. 1 0. 6 -0. 4 0. 5 0. 4 -0. 3 0. 1 0. 6 0. 4 -0. 5 4. 0 0. 4 -0. 3 -0. 5 -0. 2 0. 4 0. 5 5. 0 0. 4 -0. 6 0. 4 -0. 4 0. 0 � Pre-processing: § Build Laplacian matrix L of the graph � Decomposition: § Find eigenvalues and eigenvectors x of the matrix L § Map vertices to corresponding components of 2 1/1/2022 = 3. 0 1 0. 3 2 0. 6 3 0. 3 4 -0. 3 5 -0. 3 6 -0. 6 X= Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu How do we now find clusters? 43

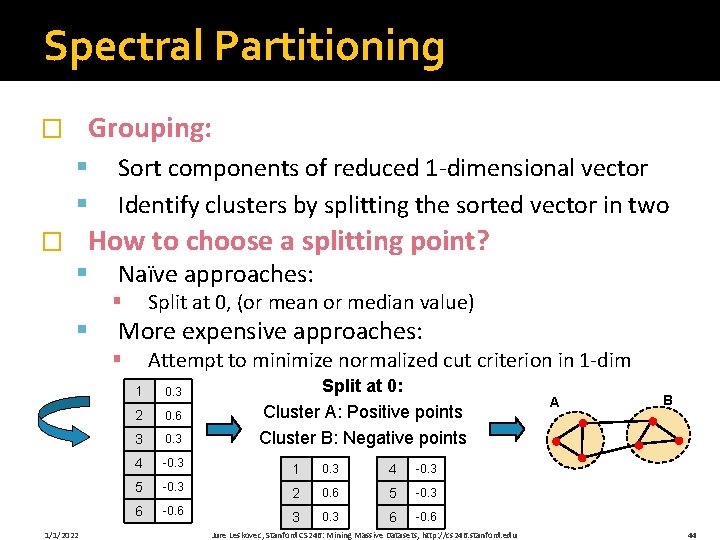
Spectral Partitioning Grouping: � § § Sort components of reduced 1 -dimensional vector Identify clusters by splitting the sorted vector in two How to choose a splitting point? � § Naïve approaches: Split at 0, (or mean or median value) § § More expensive approaches: Attempt to minimize normalized cut criterion in 1 -dim § 1/1/2022 Split at 0: Cluster A: Positive points Cluster B: Negative points 1 0. 3 2 0. 6 3 0. 3 4 -0. 3 1 0. 3 4 -0. 3 5 -0. 3 2 0. 6 5 -0. 3 6 -0. 6 3 0. 3 6 -0. 6 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu A B 44

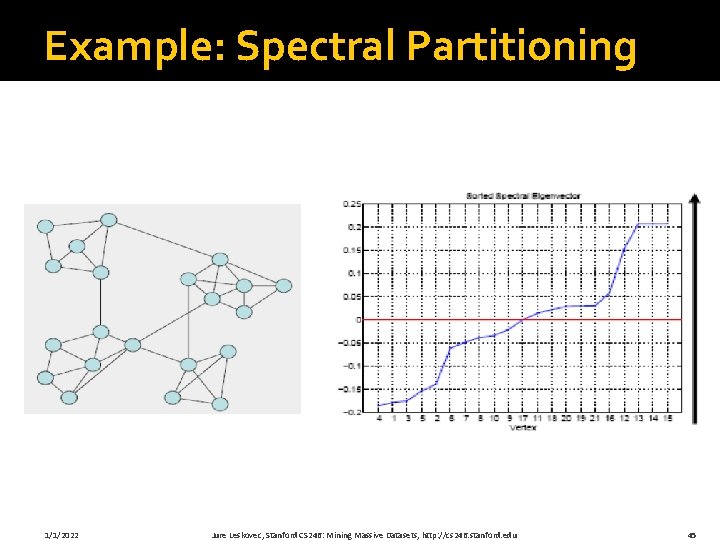
Example: Spectral Partitioning 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 45

K-Way Spectral Clustering �How do we partition a graph into k clusters? �Two basic approaches: § Recursive bi-partitioning [Hagen et al. , ’ 92] § Recursively apply bi-partitioning algorithm in a hierarchical divisive manner § Disadvantages: Inefficient, unstable § Cluster multiple eigenvectors [Shi-Malik, ’ 00] § Build a reduced space from multiple eigenvectors § Node i is described by its k eigenvector components (x 2, i, x 3, i, …, xk, i) § Use k-means to cluster the points § A preferable approach… 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 46

How to select k? �Eigengap: § The difference between two consecutive eigenvalues �Most stable clustering is generally given by the value k that maximizes the eigengap �Example: λ 1 λ 2 1/1/2022 Þ Choose k=2 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 47

How to compute λ 2? � 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 48

How to compute λ 2? � 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 49

How to compute λ 2? Summary � 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 50

Many other partitioning methods �METIS: § Heuristic but works really well in practice § http: //glaros. dtc. umn. edu/gkhome/views/metis �Graclus: § Based on kernel k-means § http: //www. cs. utexas. edu/users/dml/Software/graclus. html �Cluto: § http: //glaros. dtc. umn. edu/gkhome/views/cluto/ 1/1/2022 Jure Leskovec, Stanford CS 246: Mining Massive Datasets, http: //cs 246. stanford. edu 52