Discounted Cash Flow Approach Annuity Perpetuity Recap Previous

Discounted Cash Flow Approach– Annuity & Perpetuity

Recap § Previous class, we learn: § Future and Present Value of Multiple Cash Flows. § Let’s remember some important concepts: § Compounding period/Payment period (Monthly vs. Quarterly vs. Annual) – Inputs (to solve the question) depends on this information. § Decimals while using the formulas - % while using the calculator! § Entering “-” for PV and “+” FV – Intuition! Annuity 2

Annuity § What is “Annuity”? § An annuity is an investment paying a fixed amount dollars (payments, PMT) at the end of each period for T periods 0 1 2 3 PMT PMT … … T PMT § Key words: § Fixed payments amount (PMT) § Fixed periods (T periods) Annuity 3

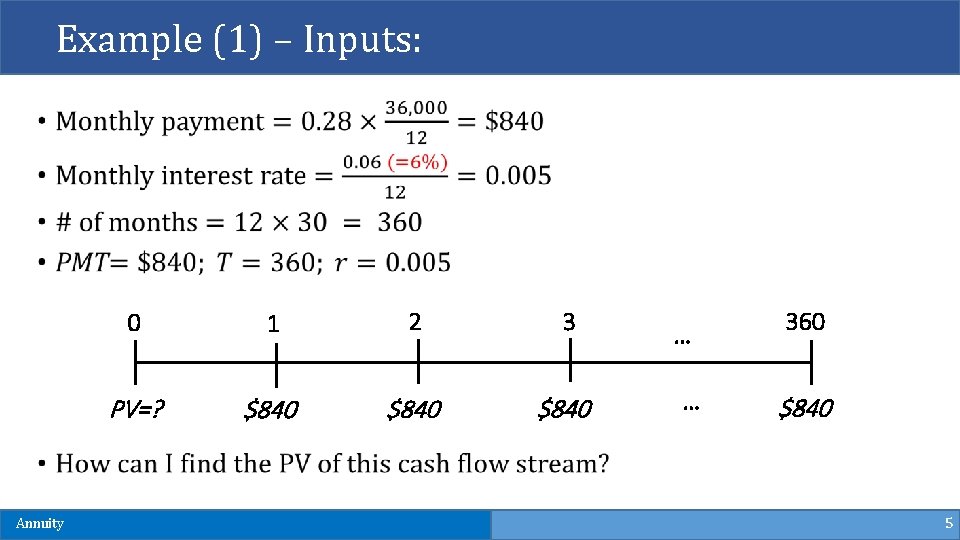
Example (1) – PV of Annuity § You have an annual salary of $36, 000 and plan to take a loan to buy a house. The bank is willing to allow you to take a mortgage for 30 years with monthly payment equal to 28% of your monthly income. The bank asks for 6% annual interest rate on the mortgage. How much is the bank willing to lend you now? Annuity 4

Example (1) – Inputs: Annuity 0 1 2 3 PV=? $840 … … 360 $840 5

Example (1) – PV of Annuity § Solution I: Let’s use what we know: Annuity 0 1 2 3 PV=? $840 … … 360 $840 6

Example (1) – PV of Annuity 7

Example (1) – PV of Annuity N = 360 I/YR = 0. 5 PV =? PMT = - 840 FV Annuity = 140, 105 =0 8

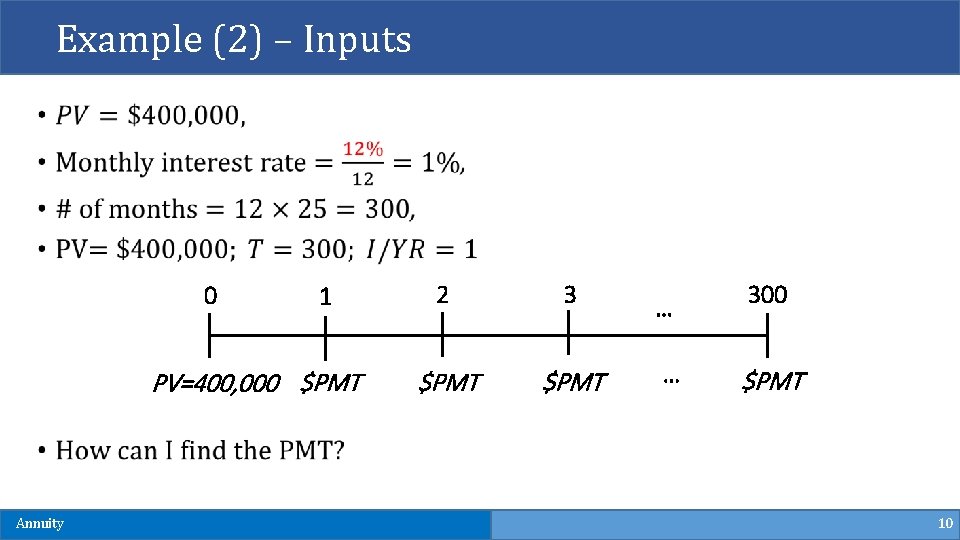
Example (2) – Mortgage Payments § Mr. Smith has arranged for a 25 -year mortgage loan of $400, 000. The annual interest rate on the loan is 12%. The bank requires Mr. Smith to make payments at the end of every month. How much is each payment? Annuity 9

Example (2) – Inputs 0 1 PV=400, 000 $PMT Annuity 2 3 $PMT … … 300 $PMT 10

Example (2) – Mortgage Payments N I/YR PV Annuity = 300 =1 = 400, 000 PMT =? FV =0 = -4, 212. 90 11

Example (2) – Mortgage Payments Annuity 12

Example (3) – Number of Periods § Mr. Smith has arranged for a mortgage loan of $200, 000. The annual rate on the loan is 12%. The bank requires Mr. Smith to make payments of $4, 212. 90 at the end of every month. How many payments will Mr. Smith have to make? Annuity 13

Example (3) – Inputs 0 PV=$200, 000 Annuity 1 $4, 212. 90 2 $4, 212. 90 3 $4, 212. 90 … … N=? $4, 212. 90 14

Example (3) – Number of Periods N =? I/YR =1 PV PMT FV Annuity = 64. 71 = 200, 000 = -4, 212. 90 =0 15

Example (3) – Number of Periods Annuity 16

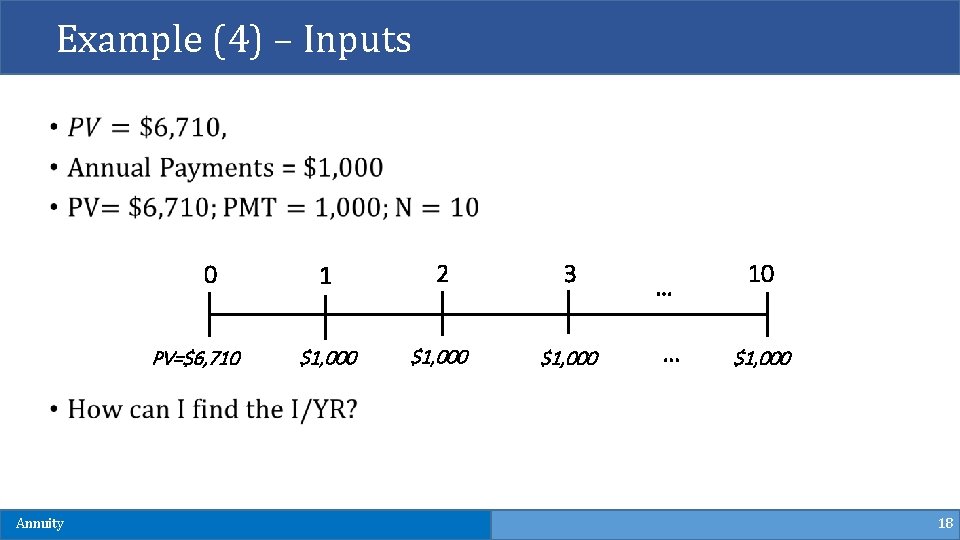
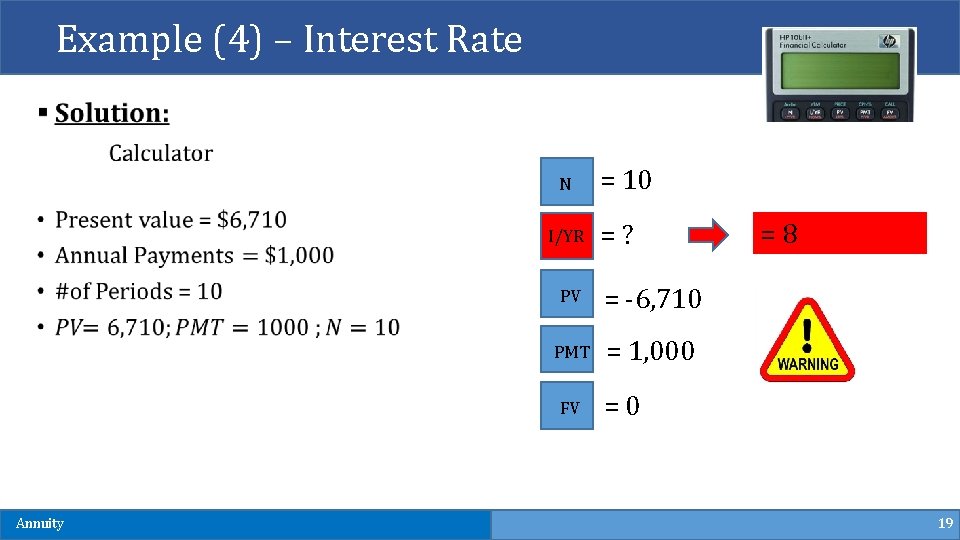
Example (4) – Interest Rate § An Insurance company offers to pay your $1, 000 per year for 10 years if you pay $6, 710 up front. What is the interest rate in this 10 -year annuity? Annuity 17

Example (4) – Inputs 0 PV=$6, 710 Annuity 1 2 3 $1, 000 … … 10 $1, 000 18

Example (4) – Interest Rate N I/YR =? PV = -6, 710 PMT = 1, 000 FV Annuity = 10 =8 =0 19

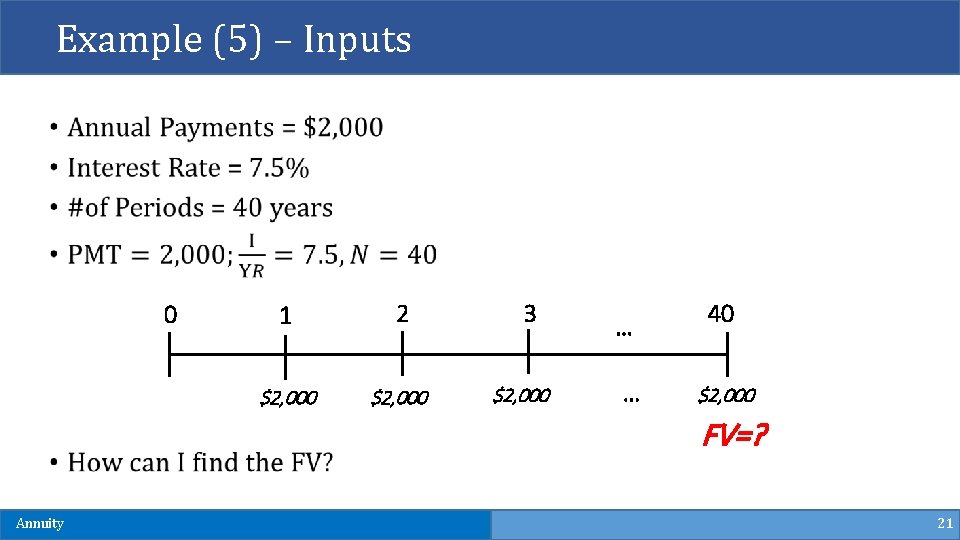
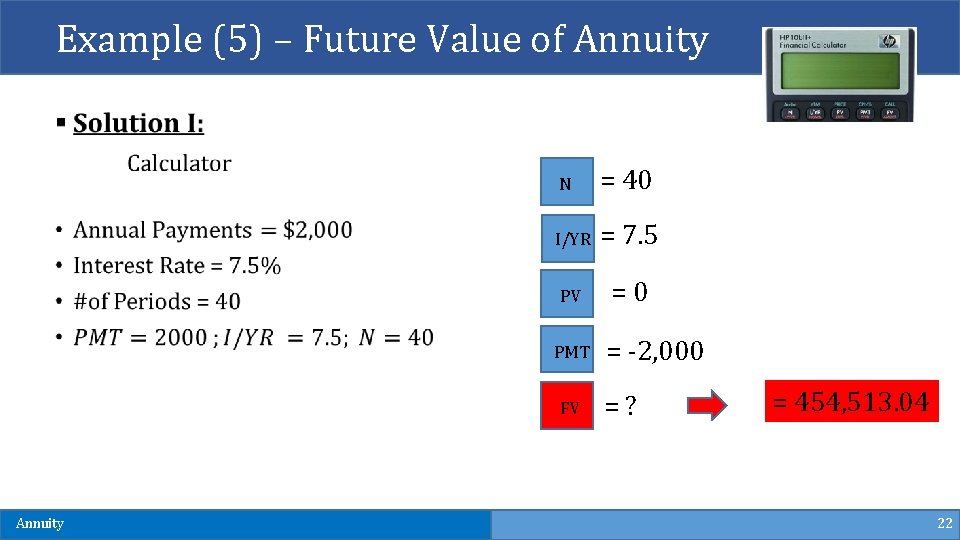
Example (5) – Future Value of Annuity § Suppose you begin saving for your retirement by depositing $2, 000 per year in a bank. If the annual interest rate is 7. 5%, how much will you have in 40 years? Annuity 20

Example (5) – Inputs 0 1 2 $2, 000 3 $2, 000 … … 40 $2, 000 FV=? Annuity 21

Example (5) – Future Value of Annuity N = 40 I/YR = 7. 5 PV =0 PMT FV Annuity = -2, 000 =? = 454, 513. 04 22

Example (5) – Future Value of Annuity 23

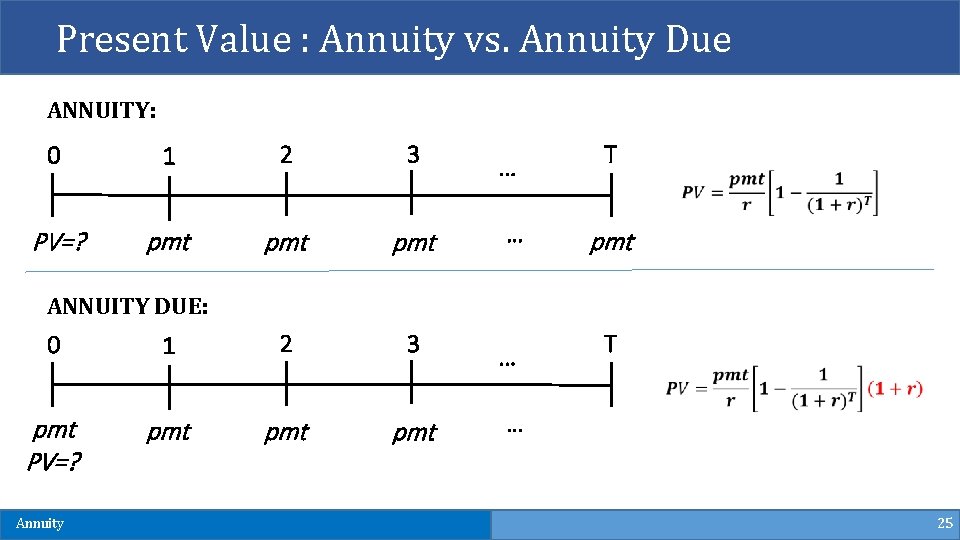
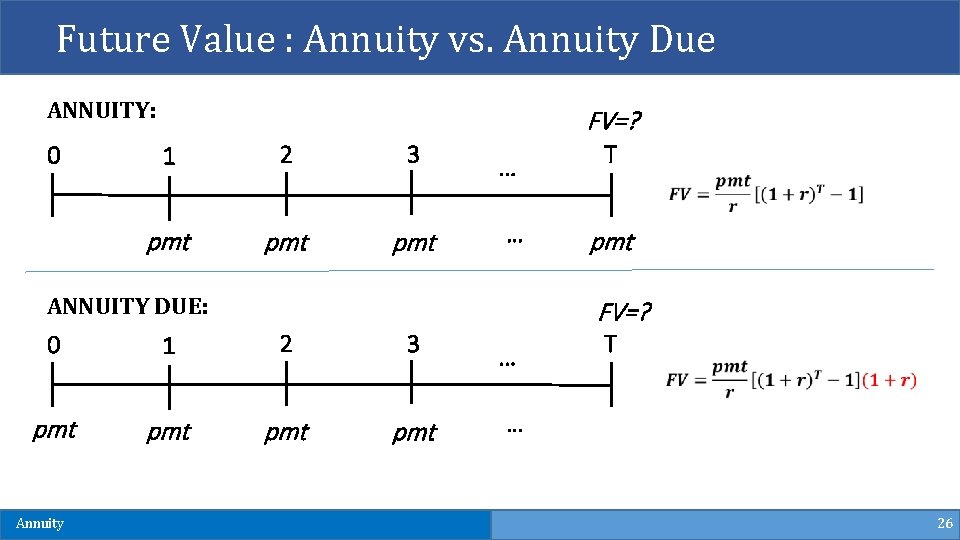
Annuity Due § So far, we have only discussed ordinary annuities. These are the most important, but there is a variation that is fairly common. § Remember that with an ordinary annuity, the cash flows occur at the end of each period. § When you take out a loan with monthly payments, for example, the first loan payment normally occurs one month after you get the loan. § However, when you lease an apartment, the first lease payment is usually due immediately. The second payment is due at the beginning of the second month, and so on. § A lease is an example of an annuity due. An annuity due is an annuity for which the cash flows occur at the beginning of each period. Annuity 24

Present Value : Annuity vs. Annuity Due ANNUITY: 0 1 2 3 PV=? pmt pmt … … T pmt ANNUITY DUE: 0 1 2 3 pmt PV=? pmt pmt Annuity … T … 25

Future Value : Annuity vs. Annuity Due ANNUITY: 0 FV=? 1 2 3 pmt pmt … … ANNUITY DUE: 0 1 2 3 pmt pmt Annuity T pmt FV=? … T … 26

Example (6) – PV of Annuity Due § You want to receive $20, 000 at the beginning of each year after retire. If you can earn 1% per year and you expect to need the income for 10 years, how much do you need to have in your account at retirement? Annuity

Example (6) – PV of Annuity Due N I/YR =1 PV =? PMT = 20, 000 FV Annuity = 10 =0 = 189, 426. 1 28 28

Example (7) – FV of Annuity Due § You are saving for a new house and you put $10, 000 per year in an account paying 8%. The deposit is made at the beginning of each year. How much will you have at the end of year 3? Annuity 29

Example (7) – FV of Annuity Due N =3 I/YR =8 PV PMT FV Annuity =0 = -10, 000 =? = 32, 464 30

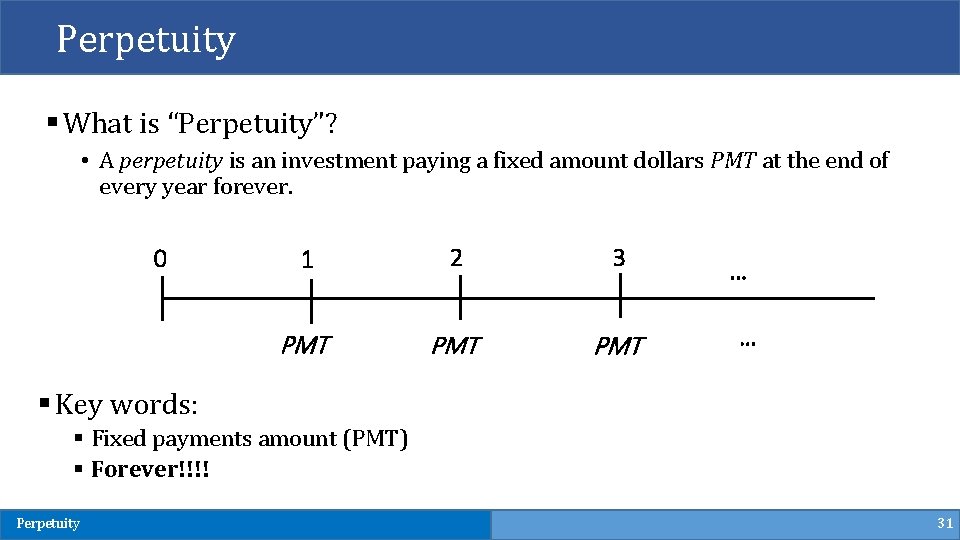
Perpetuity § What is “Perpetuity”? • A perpetuity is an investment paying a fixed amount dollars PMT at the end of every year forever. 0 1 2 3 PMT PMT … … § Key words: § Fixed payments amount (PMT) § Forever!!!! Perpetuity 31

Example (8) – Scholarship Fund • A rich entrepreneur would like to set up a foundation that, every year, will pay $5, 000 in the form of a scholarship to one deserving undergraduate. • How much money should the entrepreneur put in the foundation’s account, if that account earns 8% annually? Perpetuity 32

Example (8) – Cont’d 0 1 2 3 4 PV=? 5, 000 Perpetuity … … 33

Example (8) – Solution Perpetuity 34

Example (9) – Trust Fund Perpetuity 35

Example (10) – Stock Dividend Perpetuity 36

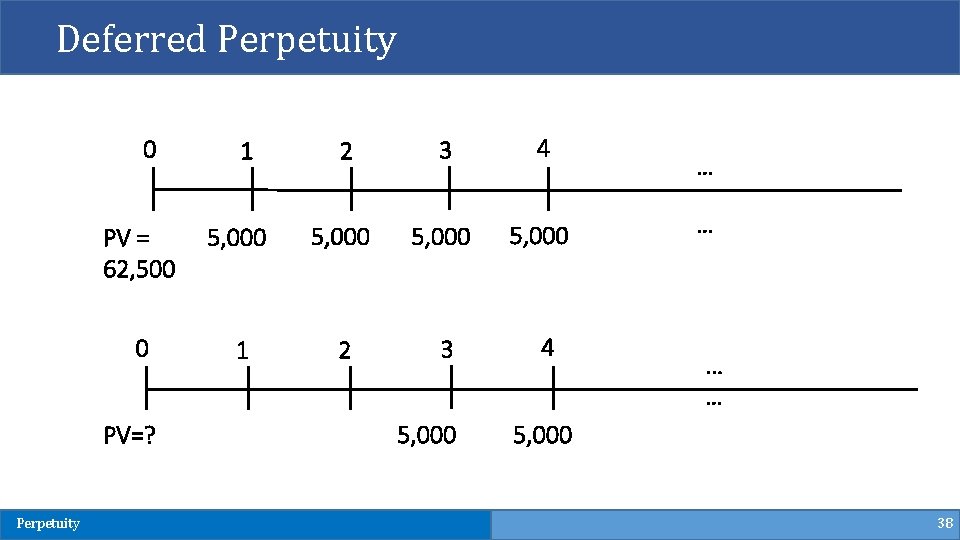
Deferred Perpetuity A rich entrepreneur would like to set up a foundation that, every year, will pay $5, 000 in the form of a scholarship to one deserving undergraduates. But after set up the foundation’s account, the university decides to make the first scholarship in three years. How much money should the entrepreneur put in the foundation’s account, if that account earns 8% annually? Perpetuity 37

Deferred Perpetuity 0 2 3 4 5, 000 PV = 62, 500 5, 000 0 1 2 3 PV=? Perpetuity 1 5, 000 4 … … 5, 000 38

A WRONG answer FOR the Deferred Perpetuity WHY? ? Perpetuity 39

Deferred Perpetuity – Step 1 0 1 2 3 5, 000 Perpetuity 4 … … 5, 000 40

Deferred Perpetuity – Step 2 0 1 2 … … $62, 500 Perpetuity 41

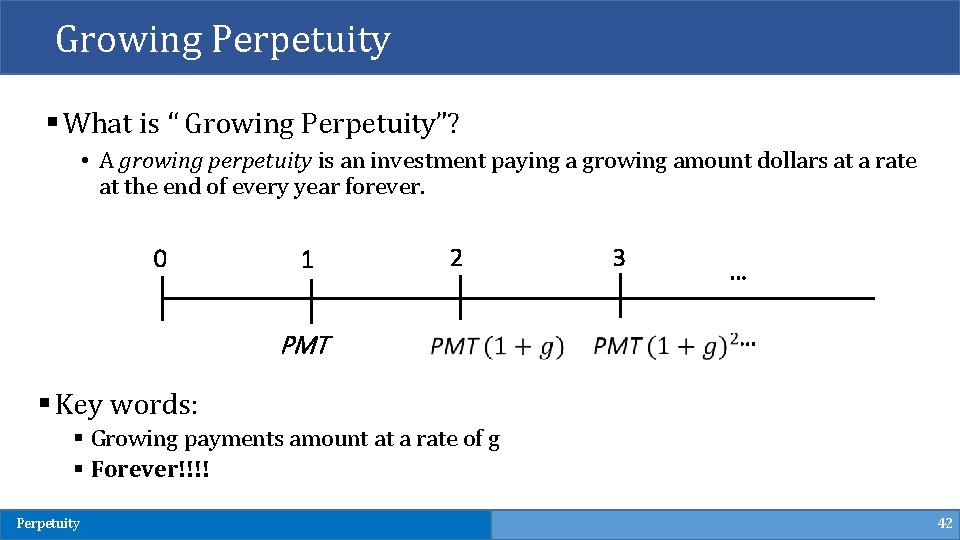
Growing Perpetuity § What is “ Growing Perpetuity”? • A growing perpetuity is an investment paying a growing amount dollars at a rate at the end of every year forever. 0 1 2 PMT 3 … … § Key words: § Growing payments amount at a rate of g § Forever!!!! Perpetuity 42

Example (11) - Project Cash Flows 0 Perpetuity 1 2 3 … 43

Example (11) – Answer Perpetuity 44

Example (12) – An Endowed Chair Perpetuity 45

Example (13) – Stock Price § Solar Energy, Inc. will pay an annual dividend of $1. 85 next year. The company just announced that future dividends will be increasing by 2% annually. How much are you willing to pay for one share of this stock if you require a 14% return? § Price = $1. 85 / (0. 14 -0. 02) = $15. 42 Perpetuity 46

APR vs. EAR § APR (Annual Percentage Rate) § It serves as a common representation of cost (return). § It is an annualized figure. § It does not provide a complete picture of these costs (Why? ) § EAR (Effective Annual Rates) § It takes into account the effects of compound interest, and is useful for evaluating loans that compound interest at regular intervals, such as monthly or daily. § Implications of the differences: § Differences between APR and EAR are most significant for loans that carry high closing costs and/or annual fees, such as mortgage loans. In this case, EAR will be much more useful in budgeting for the cost of borrowing the money. § In investing, EARs are more important for investments in which interest cannot be withdrawn midway through the term of the loan. Discounted Cash Flow Valuation 47

Example – APR to EAR § Find the Effective Annual Rate (EAR) of an 18% APR loan that is compounded monthly. =1. 1956 -1=0. 1956 or 19. 56% Discounted Cash Flow Valuation 48

Loan types § Pure Discount Loans § Interest-Only Loans § Amortized Loans Perpetuity 49

Pure Discount Loans § They are the simplest form of loan. § The borrower receives money today and repays a single lump sum (principal and interest) at a future time. § Treasury bills are excellent examples of pure discount loans. The principal amount is repaid at some future date, without any periodic interest payments. § If a T-bill promises to repay $10, 000 in 12 months and the market interest rate is 7 percent, how much will the bill sell for in the market? • PV = 10, 000 / 1. 07 = 9, 345. 79 Discounted Cash Flow Valuation 50

Interest-Only Loans § They require an interest payment each period, with full principal due at maturity. § Consider a 5 -year, interest-only loan with a 7% interest rate. The principal amount is $10, 000. Interest is paid annually. § What would the stream of cash flows be? § Years 1 – 4: Interest payments of. 07(10, 000) = 700 § Year 5: Interest + principal = 10, 700 § This cash flow stream is similar to the cash flows on corporate bonds, and we will talk about them in greater detail later. Discounted Cash Flow Valuation 51

Amortized Loans § They require repayment of principal over time, in addition to required interest. § Two Forms: § Amortized Loan with Fixed Principal Payment § Amortized Loan with Fixed Payment Discounted Cash Flow Valuation 52

Example – Excel § Loan Amount $50, 000 § Annual Interest: 8% § Loan Period=10 years § Amortized Loan with Fixed Principal Payment § Amortized Loan with Fixed Payment Discounted Cash Flow Valuation 53

Thanks! 54