DISCLAIMER This Presentation may contain Copyrighted Material DO

DISCLAIMER This Presentation may contain Copyrighted Material, DO NOT DISTRIBUTE

Geometry concepts related to Earth and Space Prepared and presented by: Souheil Zekri Wandaliz Torres

Objectives • Introduce geometry concepts that will connect visual observations of earth and space and the scientific concepts behind the observations. • Provide simple computational examples – hands-on component of the session.

Sunshine standards covered • The student measures quantities in the real world and uses the measures to solve problems. (MA. B. 1. 2) • The student estimates measurements in real-world problem situations. (MA. B. 3. 2) • The student describes, draws, identifies, and analyzes two- and three-dimensional shapes. (MA. C. 1. 2)

Sunshine standards covered • The student visualizes and illustrates ways in which shapes can be combined, subdivided, and changed. (MA. C. 2. 2) • The student uses coordinate geometry to locate objects in both two and three dimensions and to describe objects algebraically. (MA. C. 3. 2) • The student uses expressions, equations, inequalities, graphs, and formulas to represent and interpret situations. (MA. D. 2. 2)

Session Layout • Triangle geometry (angles, bisection, ratios). • Reference frames (Cartesian, cylindrical, spherical): – Hands-on solar system geometric measurements. • Introductory vector concepts. • Shape optimization and surface area to volume ratios.

• “Mathematics is the cheapest science. Unlike physics or chemistry, it does not require any expensive equipment. All one needs for mathematics is a pencil and paper. ” • "Geometry is the science of correct reasoning on incorrect figures. " » George Polya (1887 -1985)

Let’s start with a mental activity!

Let’s start with a mental activity!

Top view of a PYRAMID!

Let’s start with a mental activity! • Picture of three dimensional objects will be shown, drawn on pieces of papers. Each picture will be shown for 10 seconds and students/teachers will have to draw the exact picture out of memory afterwards. • A discussion about the way students/teachers pictured the object in their memories will follow. • Students/Teachers will be shown the actual three dimensional object made out of gum drops and sticks.

Fundamental concepts in geometry • Point: no size… just location! • Line: no edge…just direction! • Plane: no volume…just area!

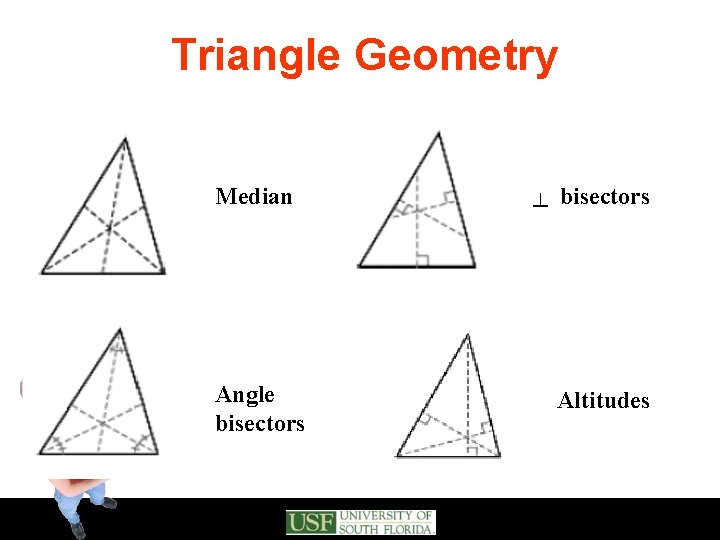
Triangle Geometry Median Angle bisectors ┴ bisectors Altitudes

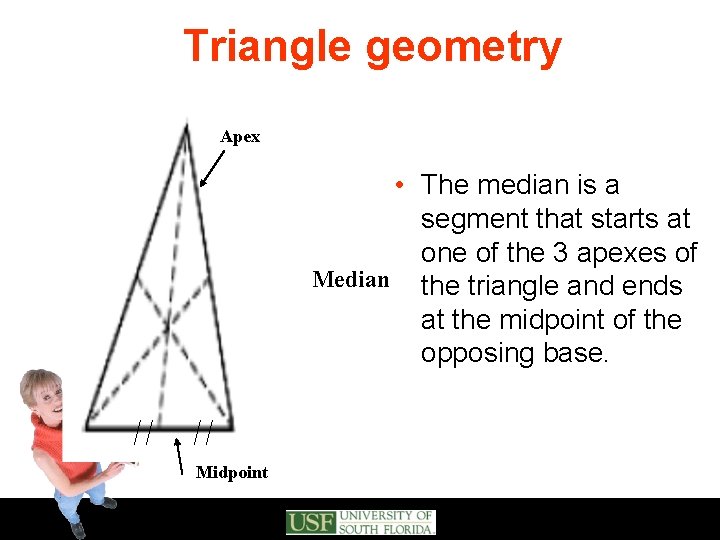
Triangle geometry Apex • The median is a segment that starts at one of the 3 apexes of Median the triangle and ends at the midpoint of the opposing base. Midpoint

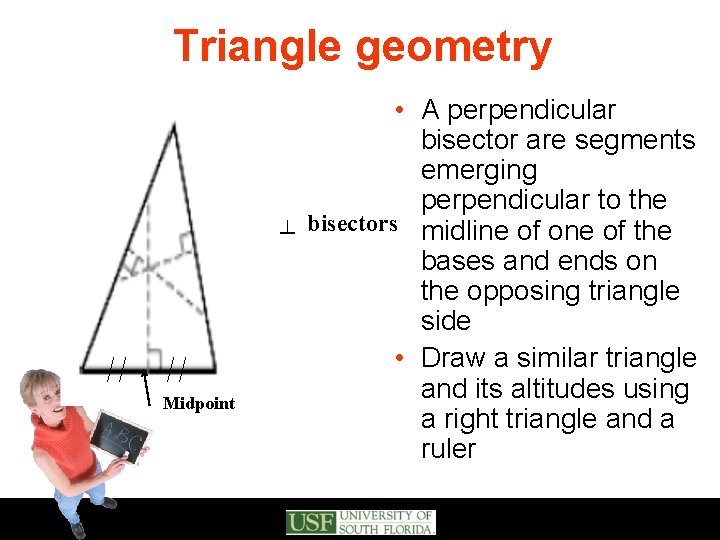
Triangle geometry ┴ Midpoint • A perpendicular bisector are segments emerging perpendicular to the bisectors midline of one of the bases and ends on the opposing triangle side • Draw a similar triangle and its altitudes using a right triangle and a ruler

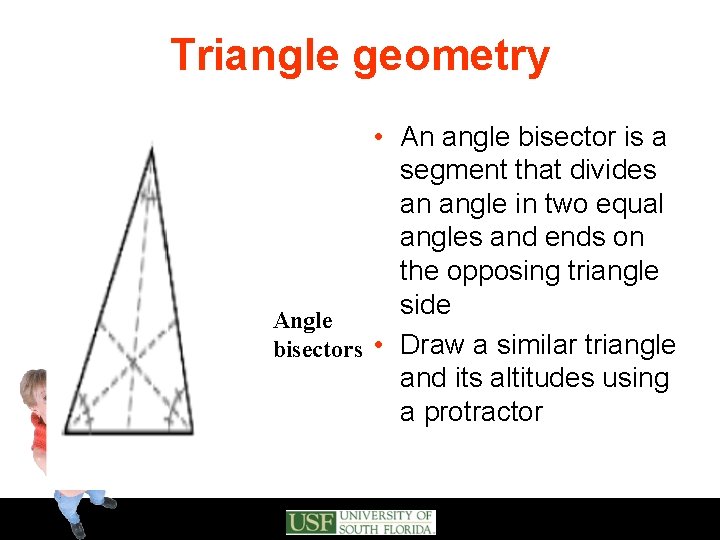
Triangle geometry • An angle bisector is a segment that divides an angle in two equal angles and ends on the opposing triangle side Angle bisectors • Draw a similar triangle and its altitudes using a protractor

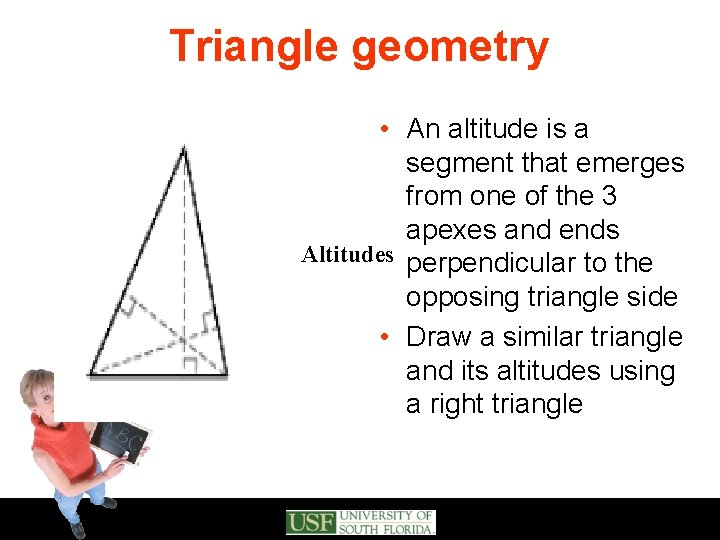
Triangle geometry • An altitude is a segment that emerges from one of the 3 apexes and ends Altitudes perpendicular to the opposing triangle side • Draw a similar triangle and its altitudes using a right triangle

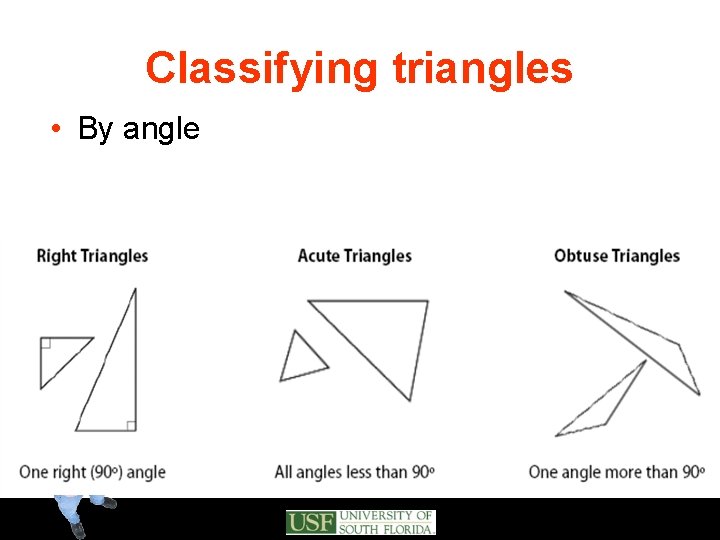
Classifying triangles • By angle

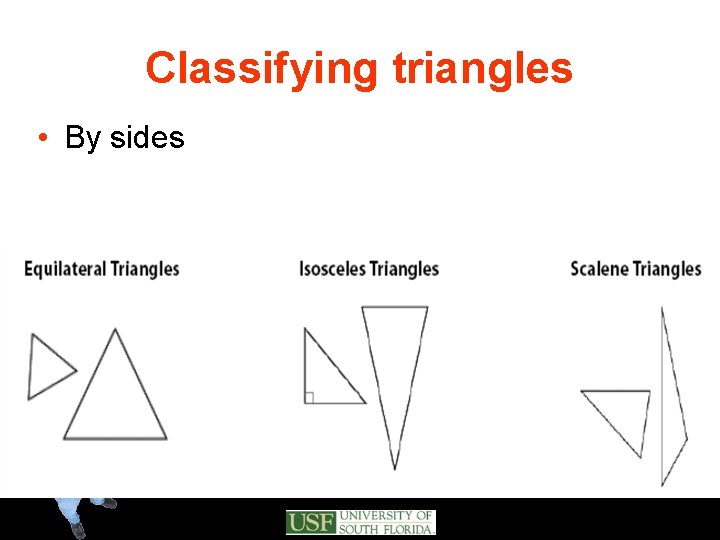
Classifying triangles • By sides

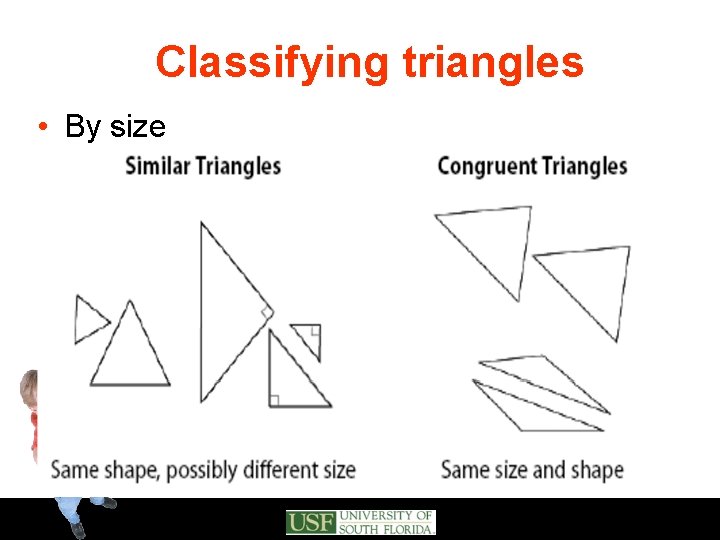
Classifying triangles • By size

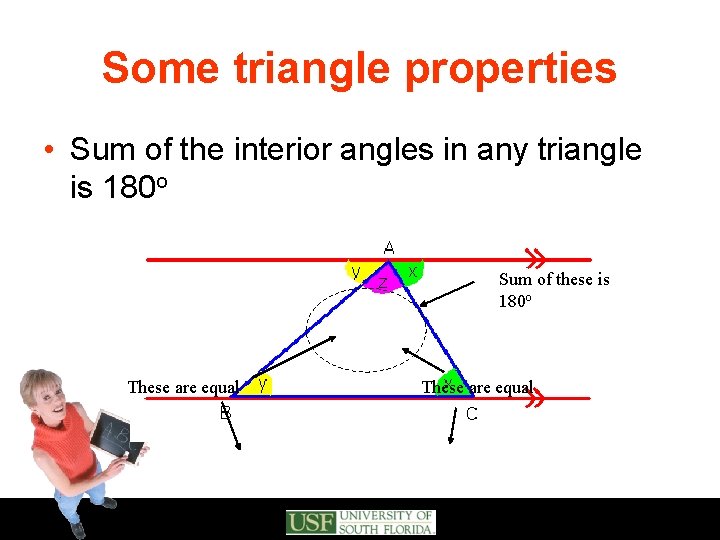
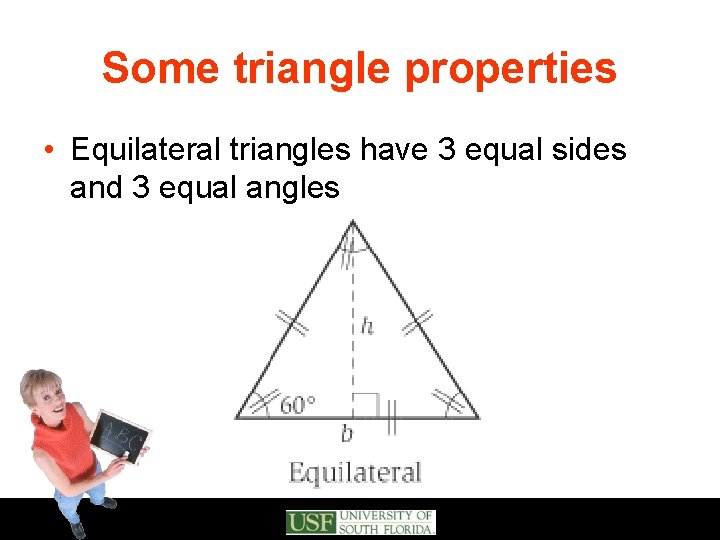
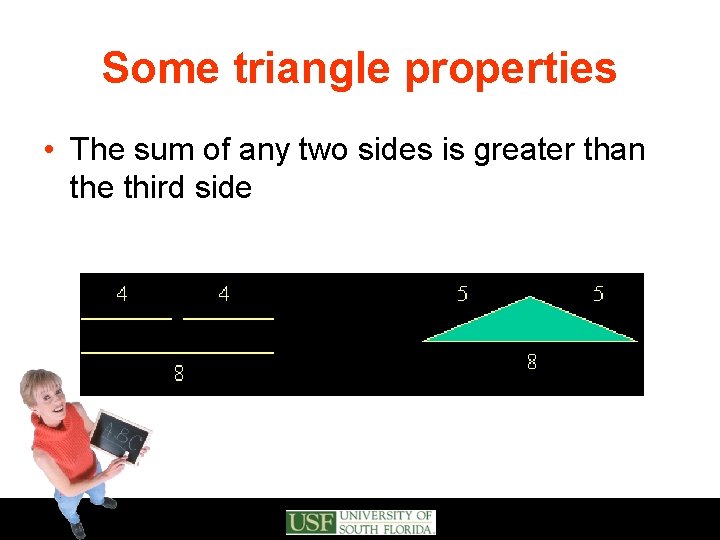
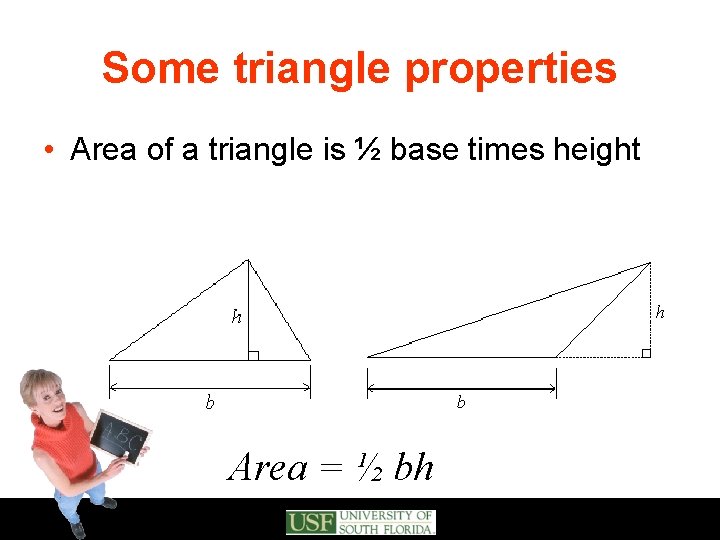
Some triangle properties • Sum of the interior angles in any triangle is 180 o • Equilateral triangles have 3 equal sides and 3 equal angles • Isosceles triangles have 2 equal sides and 2 equal angles • The sum of any two sides is greater than the third side • Area of a triangle is ½ base times height

Some triangle properties • Sum of the interior angles in any triangle is 180 o Sum of these is 180 o These are equal

Some triangle properties • Equilateral triangles have 3 equal sides and 3 equal angles

Some triangle properties • Isosceles triangles have 2 equal sides and 2 equal angles

Some triangle properties • The sum of any two sides is greater than the third side

Some triangle properties • Area of a triangle is ½ base times height Area = ½ bh

Add an activity on Triangles Suggestions: Using paper and folding it

Reference frames • • Cartesian, cylindrical and spherical The right hand rule Vectors Application of all previously introduced concepts in earth and space

Reference frames: the math way to know where everything is Every reference frame has an origin. There are 2 different type: • Cartesian frame • Polar frame (cylindrical, spherical)

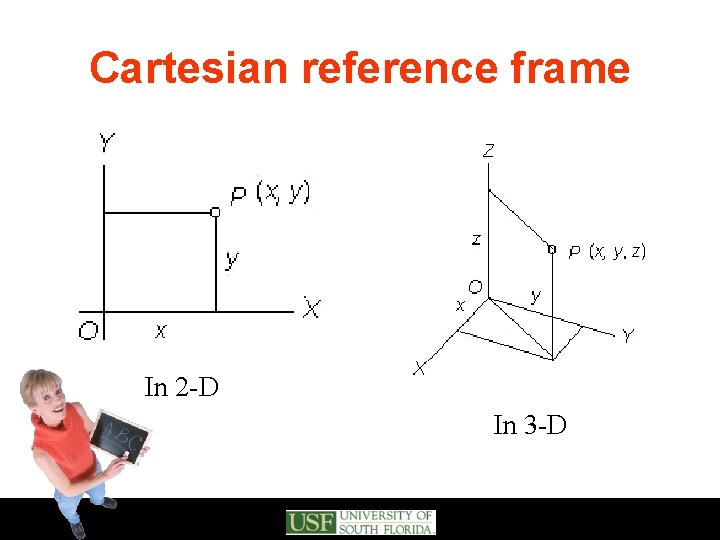
Cartesian reference frame In 2 -D In 3 -D

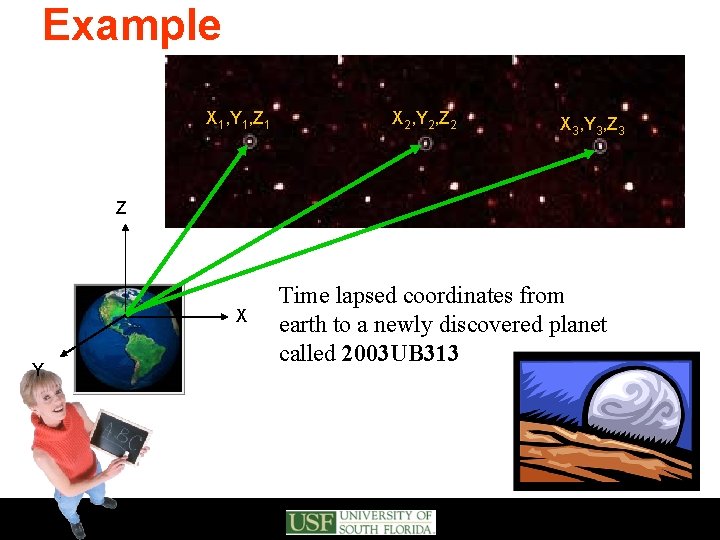
Example X 1, Y 1, Z 1 X 2, Y 2, Z 2 X 3, Y 3, Z 3 Z X Y Time lapsed coordinates from earth to a newly discovered planet called 2003 UB 313

Polar reference frame In 2 -D cylindrical In 3 -D spherical

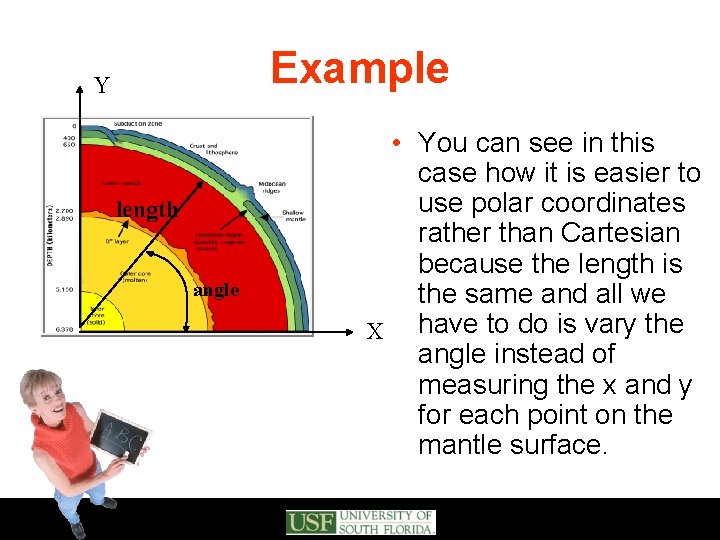
Example Y length angle • You can see in this case how it is easier to use polar coordinates rather than Cartesian because the length is the same and all we X have to do is vary the angle instead of measuring the x and y for each point on the mantle surface.

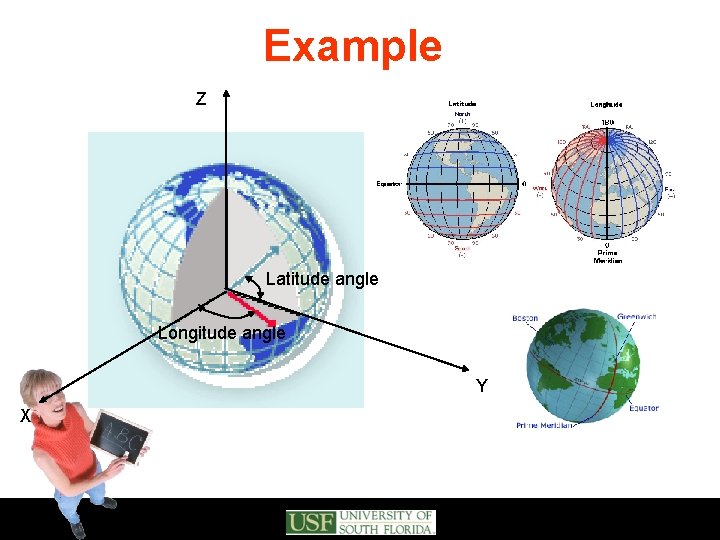
Example Z Latitude angle Φ Longitude angle Y X

Let’s locate objects in space • Using the provided reference frame and strings, find the Cartesian coordinates of different objects in the room

Data Sheet Cartesian Coordinates x Object 1 Object 2 y z

Vector concepts • What is a vector (geometrically and analytically)? • What are they used for? • How do we apply vector concepts to earth science?

Vectors or scalars: what’s the difference? • Some physical properties, such as temperature or area, are given completely by their magnitude and so only need a number are called scalar values. • There are other physical quantities, such as force, velocity or acceleration, for which we must know direction as well as size or magnitude in order to work with them. It is often very helpful to represent such quantities by directed lines called vectors

Vectors: General Rules • Two vectors are equal if and only if they are equal in both magnitude and direction • If c is a vector, then - c is defined as having the same magnitude but the reverse direction to c • Multiplying a vector by a number or scalar just has the effect of changing its scale

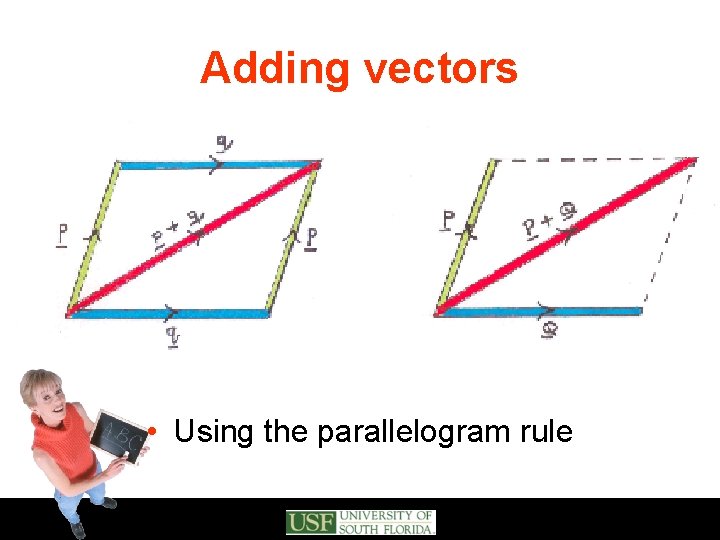
Adding vectors • Using the parallelogram rule

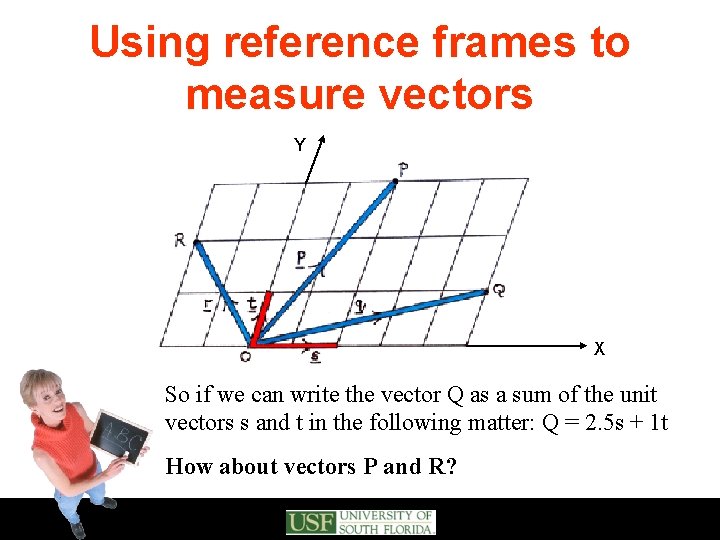
Using reference frames to measure vectors Y X So if we can write the vector Q as a sum of the unit vectors s and t in the following matter: Q = 2. 5 s + 1 t How about vectors P and R?

How do we apply vector concepts to earth science? • Combining the reference frame concepts and vector concepts we can easily see how much easier it is to locate objects (galaxies, stars, planets, satellites, comets, space ships, etc…) and calculate the speed and acceleration of any of these objects.

Add an activity on vectors, relate the concepts with similar vocab

Shape optimization and surface to volume ratios • What is surface to volume ratio? • How is a shape optimal? • Why is the Universe oval (close to being spherical) shaped?

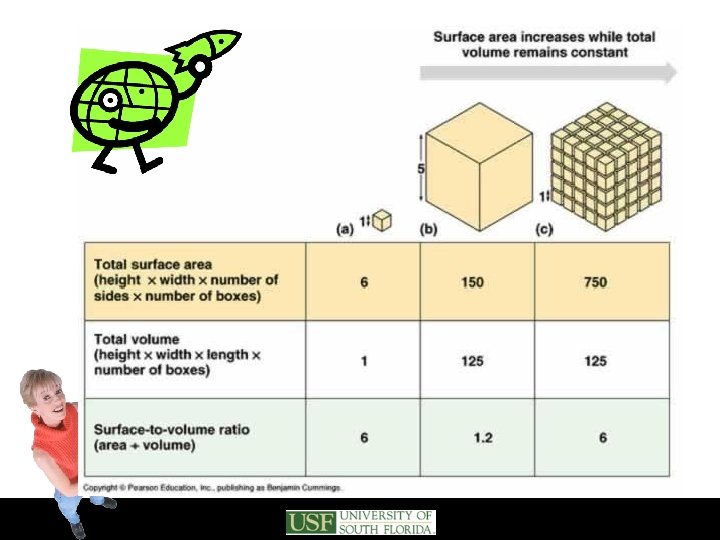
What is surface area to volume ratio? • It is the ratio (or division) of the surface area by the volume. • The larger this ratio is, the more surface there is for a specific volume. • This allows more useful area (for physical or chemical reactions) for a fixed volume.

More examples

How is a shape optimal? • The higher the ratio of surface area to volume, the more optimized the shape is. • Let’s use the following websites to compute the ratio for a sphere and a cube. (Volume is the same) – For the volume calculation use the following website: http: //grapevine. abe. msstate. edu/~fto/tools/vol/ – For the surface area calculation use the following website: http: //www. csgnetwork. com/surfareacalc. html

Data Sheet Surface Volume {V} Area 3) (m {SA}(m 2) Cube Sphere Make it work… didn’t work in class for some reason

So why is the universe oval shaped? Discussion!