Dirichlet formulation with constant potential Ana Lavern Simavilla

Dirichlet formulation with constant potential Ana Laverón Simavilla Mª Victoria Lapuerta González

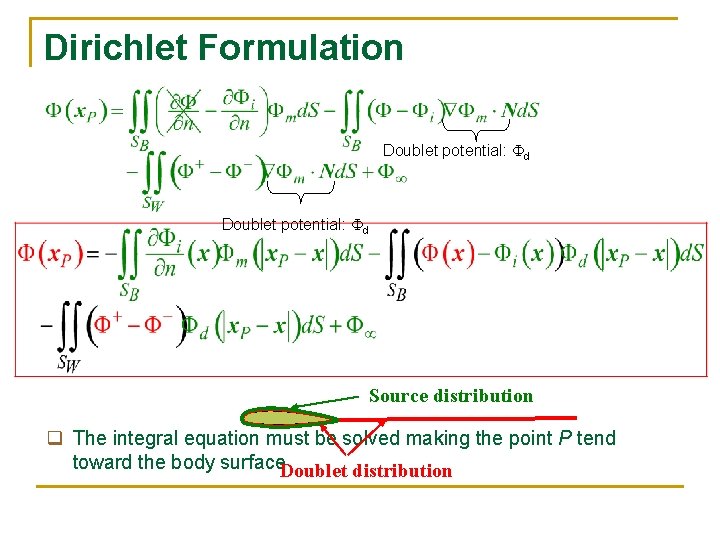
Dirichlet Formulation Doublet potential: Fd Source distribution q The integral equation must be solved making the point P tend toward the body surface. Doublet distribution

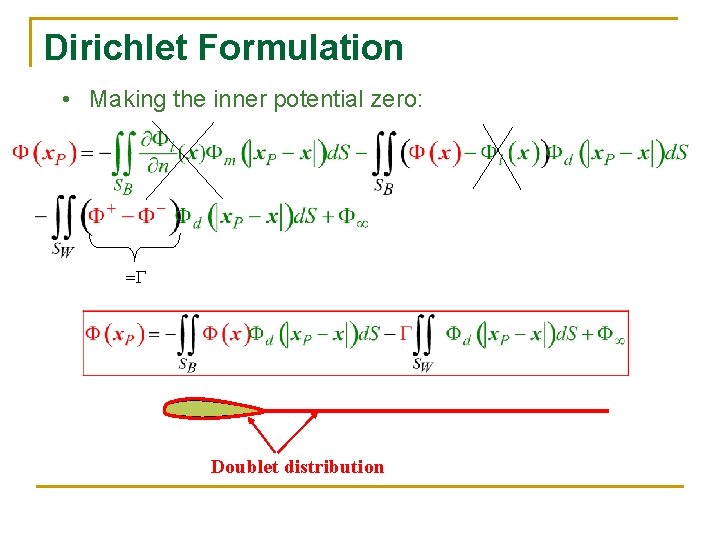
Dirichlet Formulation • Making the inner potential zero: = Doublet distribution

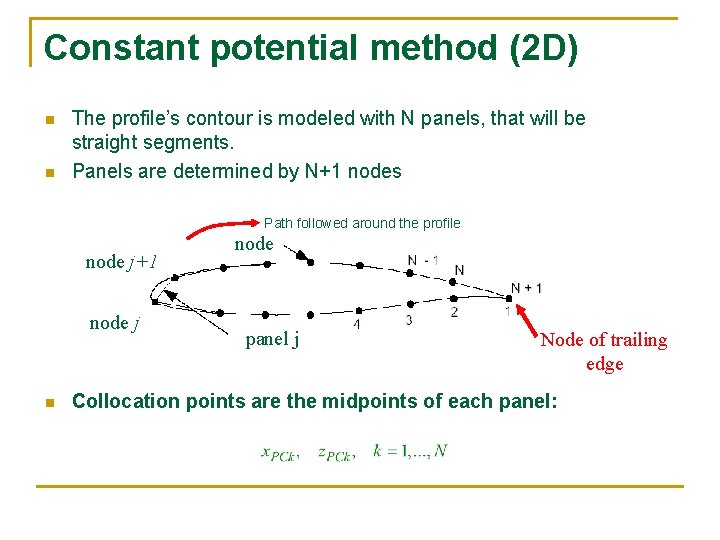
Constant potential method (2 D) n n The profile’s contour is modeled with N panels, that will be straight segments. Panels are determined by N+1 nodes Path followed around the profile node j+1 node j n node panel j Node of trailing edge Collocation points are the midpoints of each panel:

Constant potential method (2 D) The following conditions are imposed: n Constant potential on each panel n The previous equation is rewritten for the collocation points k n =FN-F 1

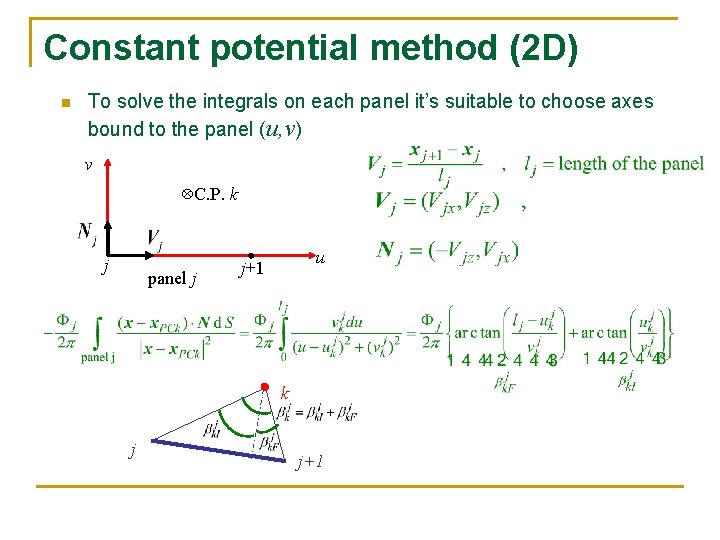
Constant potential method (2 D) n To solve the integrals on each panel it’s suitable to choose axes bound to the panel (u, v) v C. P. k j panel j u j+1 k j j+1

Constant potential method (2 D) n For the panel, k=j n For the layer surface, a semi-infinite panel is used n Finally:

Constant potential method (2 D) Matrix form: with and

Constant potential method (2 D)

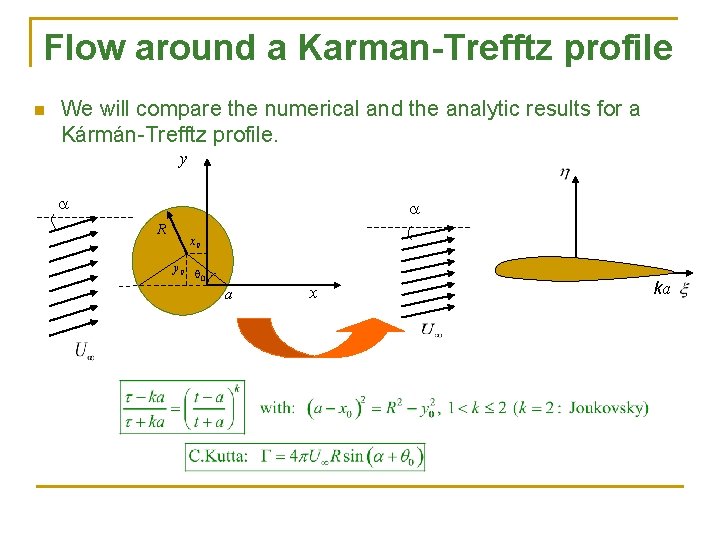
Flow around a Karman-Trefftz profile n We will compare the numerical and the analytic results for a Kármán-Trefftz profile. y a a R x 0 y 0 q 0 a x ka

Required calculations 1. For n panels calculate the pressure coefficient on the profile’s lower and upper, . For this, calculate the speed on the nodes using the expression: where di is the distance between the collocation points i and i+1. 2. Calculate the global circulation around the airfoil: 3. Compare the results with those obtained exactly using the Kármán-Trefftz transformation.

Comments for the resolution n Function that gives the nodes’ coordinates: function[ξ, η]=function_profile (n, n Function that gives the analytic value of function [ξ p, lower, t 0, k, R) : Cp, lower, ξ p, upper, Cp, upper, η p, lower, η p, upper, ] = function_karman(t 0, k, a, n_kam, R, )

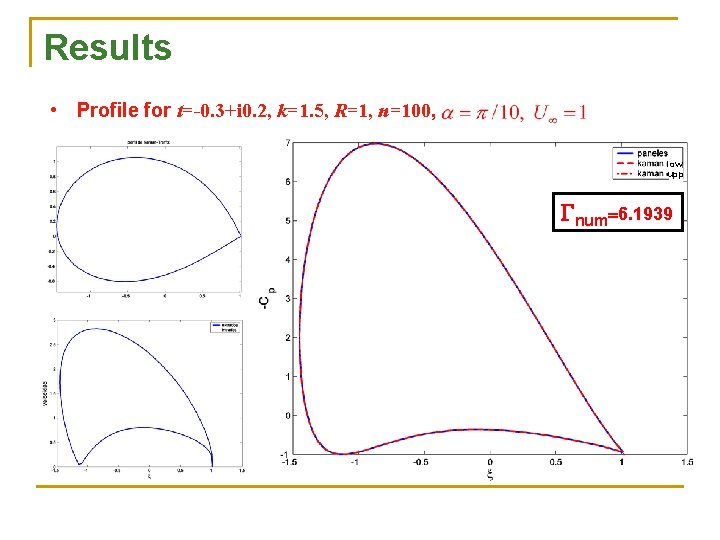
Results • Profile for t=-0. 3+i 0. 2, k=1. 5, R=1, n=100, low upp Gnum=6. 1939