Directional Statistics Data in degrees or coordinates Directional

Directional Statistics Data in degrees or coordinates

Directional Statistics • North, Northeast, 30°, 215°, etc • Standard descriptive statistics are misleading • Anything measured in degrees • Any cyclic data: daily, weekly, monthly, or yearly • Mathematical vs Geographic standards

Orientation • North/South, East/West • Orientation ignores directionality (e. g. “Texas Avenue runs both ways. ”) • Mostly roads, paths, and other transportation links

Testing for Direction • Rayleigh’s Test for directionality • Chi-Square Test for even distribution • For orientation data, we double the value and use the directionality tests

Mean Direction • Convert to rectangular form: – x = cos , y = sin [may need to convert degrees to radians] • Sum coordinates: – C = (cos i), S = (sin i) • Mean depends on sign of C, S

Mean Direction (degrees) C=0, S>0 90° C=0, S<0 270° C>0, S≥ 0 arctan(S/C) C<0 arctan(S/C) + 180 C>0, S<0 arctan(S/C) + 360

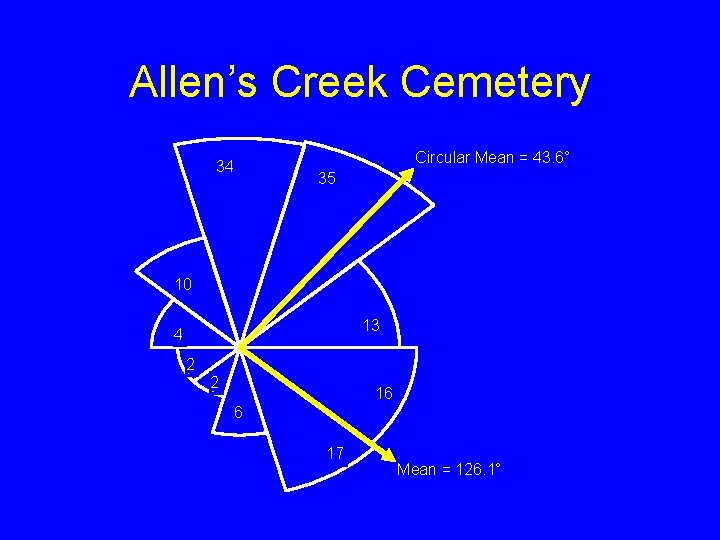
Allen’s Creek Cemetery Circular Mean = 43. 6° 34 35 10 13 4 2 2 16 6 17 Mean = 126. 1°

Rayleigh’s Test • Null hypothesis of uniformity (or bimodal opposing directions) • Based on mean angle and Rayleigh’s spread:

Chi Square • Divide data into groups: 4, 8, etc • Calculate simple Chi Square test • This ignores circular nature of the data, but provides a rough guide to finding differences

Package circular 1 • Circular object class holds information about the kind of circular data being used: – units – radians, degrees, or hours – zero – location of zero point – rotation – clockwise or counterclockwise • templates set both zero and rotation

Package circular 2 • Descriptive statistics adjusted for circular data • Plotting circular plots, density plots, rose, and windrose plots • Statistical tests for directionality, regression, and comparing samples

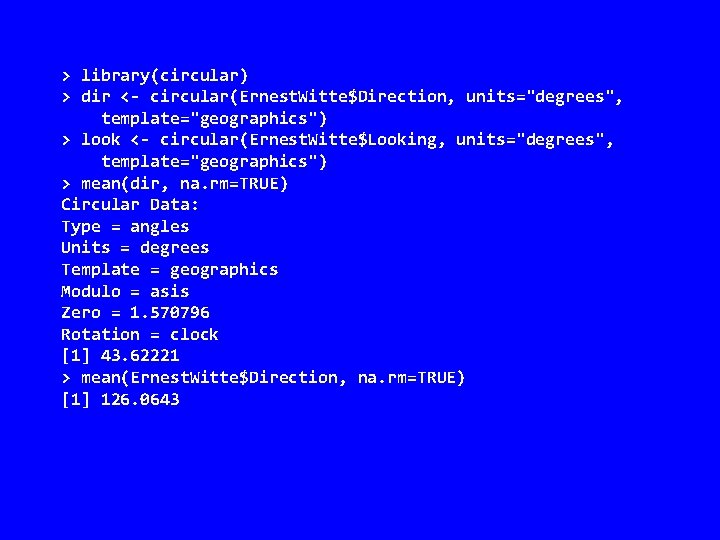
Example • Ernest Witte has two directional variables: – Direction (direction the spinal column head is pointing toward) – Looking (direction eyes are looking toward) • They are stored as geographic data (degrees clockwise from north)

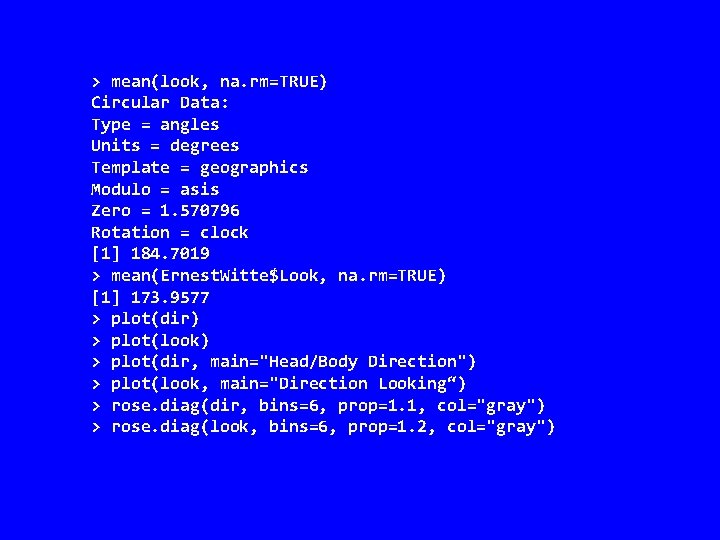
> library(circular) > dir <- circular(Ernest. Witte$Direction, units="degrees", template="geographics") > look <- circular(Ernest. Witte$Looking, units="degrees", template="geographics") > mean(dir, na. rm=TRUE) Circular Data: Type = angles Units = degrees Template = geographics Modulo = asis Zero = 1. 570796 Rotation = clock [1] 43. 62221 > mean(Ernest. Witte$Direction, na. rm=TRUE) [1] 126. 0643

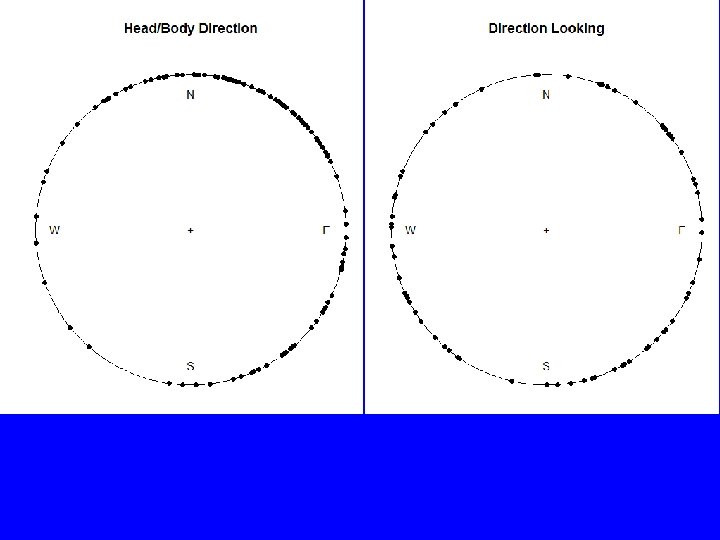
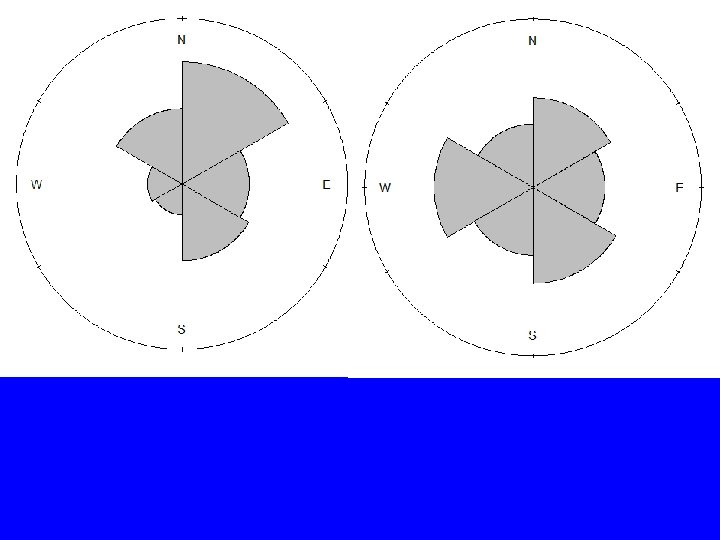
> mean(look, na. rm=TRUE) Circular Data: Type = angles Units = degrees Template = geographics Modulo = asis Zero = 1. 570796 Rotation = clock [1] 184. 7019 > mean(Ernest. Witte$Look, na. rm=TRUE) [1] 173. 9577 > plot(dir) > plot(look) > plot(dir, main="Head/Body Direction") > plot(look, main="Direction Looking“) > rose. diag(dir, bins=6, prop=1. 1, col="gray") > rose. diag(look, bins=6, prop=1. 2, col="gray")

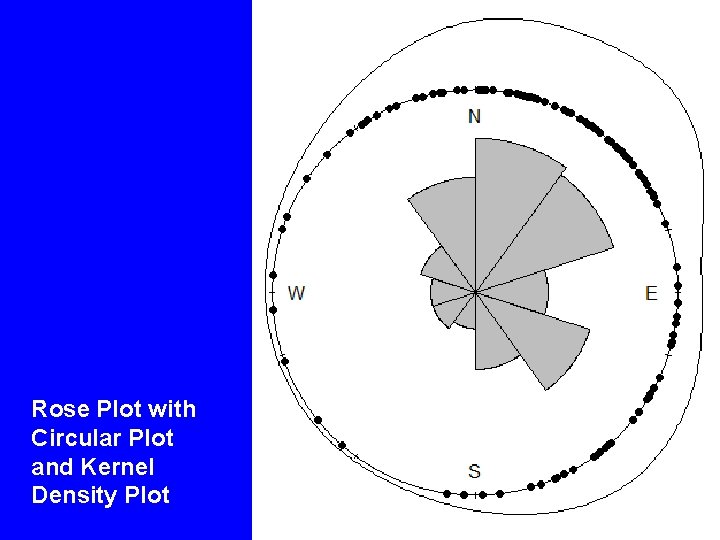
Rose Plot with Circular Plot and Kernel Density Plot

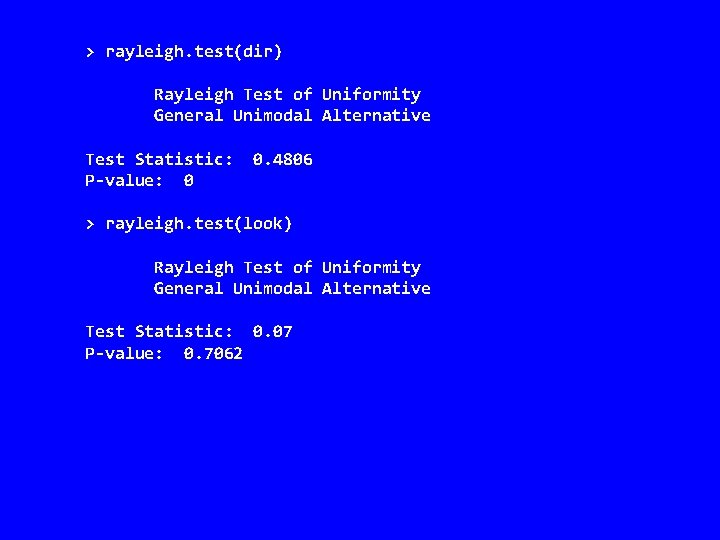
> rayleigh. test(dir) Rayleigh Test of Uniformity General Unimodal Alternative Test Statistic: P-value: 0 0. 4806 > rayleigh. test(look) Rayleigh Test of Uniformity General Unimodal Alternative Test Statistic: 0. 07 P-value: 0. 7062