Directed paths decomposition of complete multidigraph Zdzisaw Skupie

Directed paths decomposition of complete multidigraph Zdzisław Skupień Mariusz Meszka AGH UST Kraków, Poland

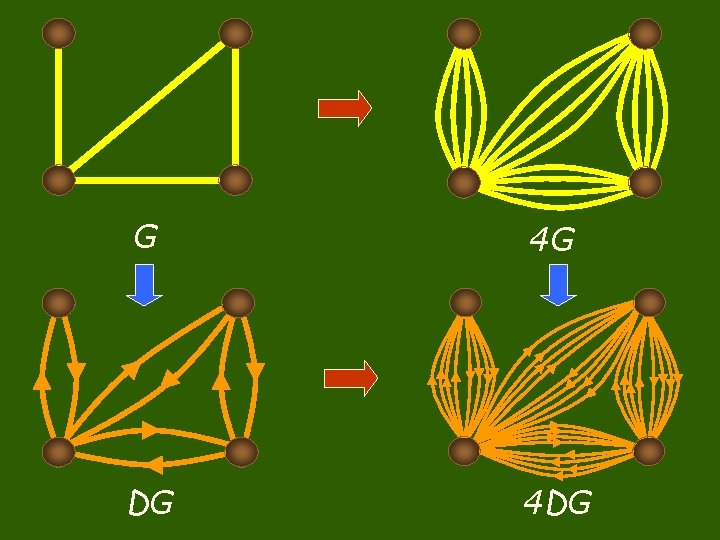
For a given graph G of order n, the symbol λG stands for a λ-multigraph on n vertices, obtained by replacing each edge of G by λ edges (with the same endvertices). If G Kn the symbol λKn denotes the complete λ-multigraph on n vertices. G 4 G

A decomposition of a multigraph G is a family of edge-disjoint submultigraphs of G which include all edges of G.

Theorem [M. Tarsi; 1983] Necessary and sufficient conditions for the existence of a decomposition of λKn into paths of length m are λn(n-1) 0 (mod 2 m) and n m+1. [C. Huang] [S. Hung, N. Mendelsohn; 1977] handcuffed designs [P. Hell, A. Rosa; 1972] resolvable handcuffed designs

Theorem [M. Tarsi; 1983] The complete multigraph λKn is decomposable into undirected paths of any lengths provided that the lengths sum up to λn(n-1)/2, each length is at most n-3 and, moreover, n is odd or λ is even. [K. Ng; 1985] improvement on any nonhamiltonian paths in the case n is odd and λ=1

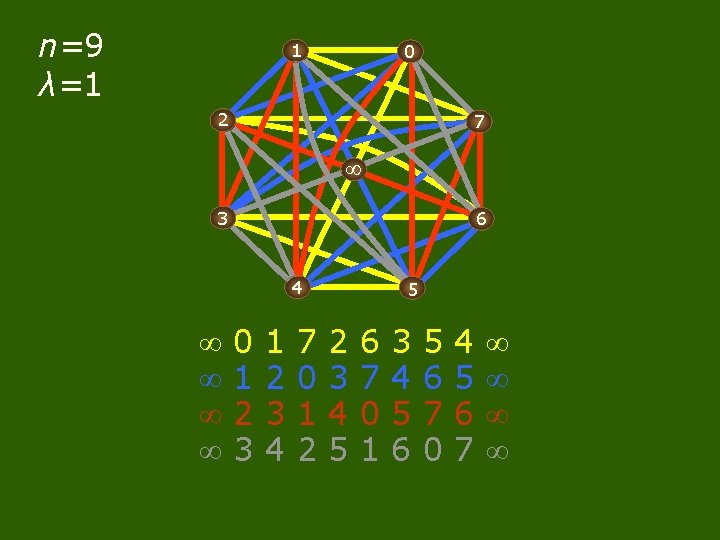
n=9 λ=1 1 0 2 7 3 6 4 0 1 2 3 4 7 0 1 2 5 2 3 4 5 6 7 0 1 3 4 5 6 7 0 4 5 6 7

Conjecture [M. Tarsi; 1983] The complete multigraph λKn is decomposable into undirected paths of arbitrarily prescribed lengths provided that the lengths sum up to λn(n-1)/2.

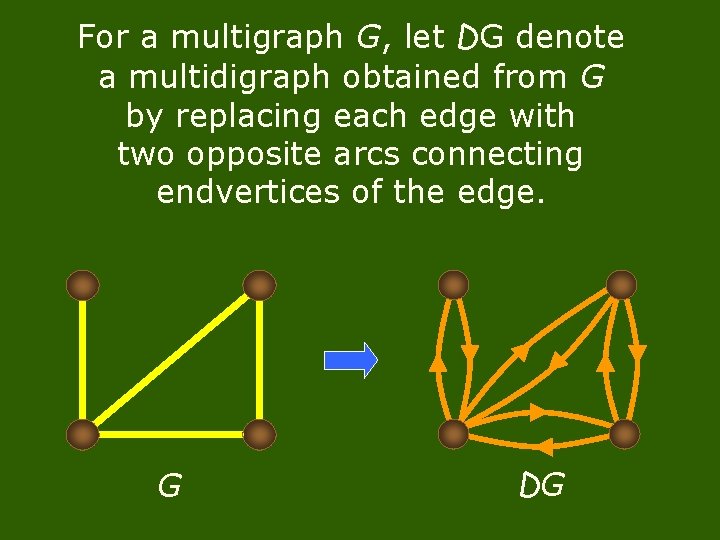
For a multigraph G, let DG denote a multidigraph obtained from G by replacing each edge with two opposite arcs connecting endvertices of the edge. G DG

For a given graph G digraph D of order n, the symbol λG λD stands for a λ-multigraph on n vertices, obtained by replacing λ-multidigraph edgeobtained of G by λ on n each vertices, byedges replacing (with same each the edge of Gendvertices). by λ edges arcsame of D endvertices). arcs (with the same endvertices). The symbol λDKn denotes the complete λ-multidigraph on n vertices.

G 4 G DG 4 DG

A decomposition of a multigraph G A decomposition of a multidigraph multigraph G D is a family of edge-disjoint submultigraphs of G which include all edges of G. arc-disjoint submultidigraphs of D which include all edges of G. arcs of D

Problem [E. Strauss; ~1960] Can the complete digraph on n vertices be decomposed into n directed hamiltonian paths? [J-C. Bermond, V. Faber; 1976] even n [T. Tillson; 1980] odd n, n 7 Theorem [J. Bosák; 1986] The multigraph λDKn is decomposable into directed hamiltonian paths if and only if neither n=3 and λ is odd nor n=5 and λ=1.

Problem [Z. Skupień, M. Meszka; 1997] If the complete multidigraph λDKn is decomposable into directed paths of arbitrarily prescribed lengths then the lengths must sum up to λn(n-1), and moreover all paths cannot be hamiltonian if either n=3 and λ is odd or n=5 and λ=1. Are the above necessary conditions also sufficient for the existence of a decomposition into given paths?

Theorem [Z. Skupień, M. Meszka; 1999] For n 3, the complete multidigraph λDKn is decomposable into directed nonhamiltonian paths of arbitrarily prescribed lengths ( n-2) provided that the lengths sum up to λn(n-1). Theorem [Z. Skupień, M. Meszka; 2004] For n 4, the complete multidigraph λDKn is decomposable into directed paths of arbitrarily prescribed lengths except the length n-2, provided that the lengths sum up to λn(n-1), unless all paths are hamiltonian and either n=3 and λ is odd or n=5 and λ=1.

Corollary [Z. Skupień, M. Meszka; 2004] Necessary and sufficient conditions for the existence of a decomposition of λDKn into directed paths of the same length m are λn(n-1) 0 (mod m) and m n-1, unless m=n-1 and either n=3 and λ is odd or n=5 and λ=1.

Conjecture [Z. Skupień, M. Meszka; 2000] The complete multidigraph λDKn is decomposable into directed paths of arbitrarily prescribed lengths provided that the lengths sum up to λn(n-1), unless all paths are hamiltonian and either n=3 and λ is odd or n=5 and λ=1.