Direct Variation Lesson 5 5 Algebra 1 Additional

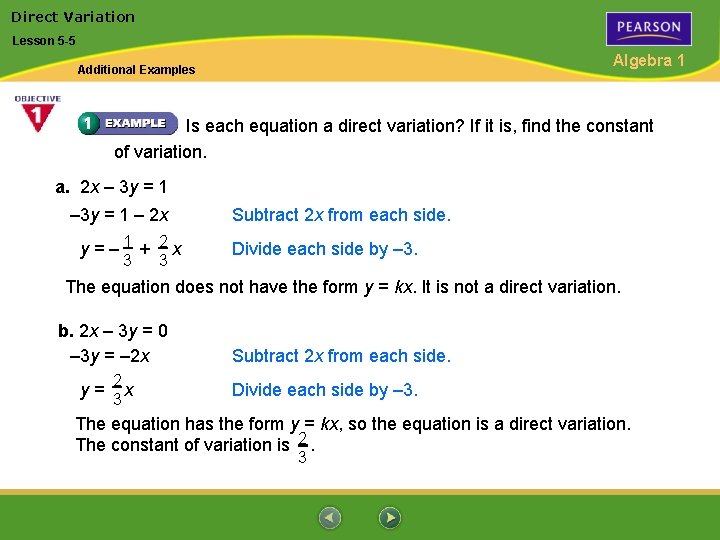
Direct Variation Lesson 5 -5 Algebra 1 Additional Examples Is each equation a direct variation? If it is, find the constant of variation. a. 2 x – 3 y = 1 – 2 x y=– 1 + 2 x 3 3 Subtract 2 x from each side. Divide each side by – 3. The equation does not have the form y = kx. It is not a direct variation. b. 2 x – 3 y = 0 – 3 y = – 2 x y= 2 x 3 Subtract 2 x from each side. Divide each side by – 3. The equation has the form y = kx, so the equation is a direct variation. The constant of variation is 2. 3

Direct Variation Lesson 5 -5 Algebra 1 Additional Examples Write an equation for the direct variation that includes the point (– 3, 2). y = kx Use the general form of a direct variation. 2 = k(– 3) Substitute – 3 for x and 2 for y. 2 – 3=k Divide each side by – 3 to solve for k. 2 y = – 3 x 2 Write an equation. Substitute – 3 for k in y = kx. 2 The equation of the direct variation is y = – 3 x.

Direct Variation Lesson 5 -5 Additional Examples Algebra 1 The weight an object exerts on a scale varies directly with the mass of the object. If a bowling ball has a mass of 6 kg, the scale reads 59. Write an equation for the relationship between weight and mass. Relate: The weight varies directly with the mass. When x = 6, y = 59. Define: Let x = the mass of an object. Let y = the weight of an object.

Direct Variation Lesson 5 -5 Algebra 1 Additional Examples (continued) Write: y = k x Use the general form of a direct variation. 59 = k(6) Solve for k. Substitute 6 for x and 59 for y. 59 =k 6 Divide each side by 6 to solve for k. 59 Write an equation. Substitute 59 for k in y = kx. y= 6 x 6 The equation y = 59 x relates the weight of an object to its mass. 6

Direct Variation Lesson 5 -5 Algebra 1 Additional Examples y For the data in each table, use the ratio x to tell whether y varies directly with x. If it does, write an equation for the direct variation. a. x y y x b. x 1 1 = – 0. 5 – 2 – 1 2 2 – 1 = – 0. 5 2 1 2 4 – 2 = – 0. 5 4 2 – 4 – 2 Yes, the constant of variation is – 0. 5. The equation is y = – 0. 5 x. y x y 2 = – 2 – 1 2 =2 1 – 4 = – 2 2 y No, the ratio x is not the same for each pair of data.

Direct Variation Lesson 5 -5 Algebra 1 Additional Examples Suppose a windlass requires 0. 75 lb of force to lift an object that weighs 48 lb. How much force would you need to lift 210 lb? Relate: The force of 0. 75 lb lifts 48 lb. The force of n lb lifts 210 lb. Define: Let n = the force you need to lift 210 lb. Write: force 1 force 2 = weight 1 weight 2 0. 75 n = 48 210 0. 75(210) = 48 n n ≈ 3. 3 Use a proportion. Substitute 0. 75 force 1, 48 for weight 1, and 210 for weight 2. Use cross products. Solve for n. You need about 3. 3 lb of force to lift 210 lb.