Direct Variation Learn to recognize direct variation and




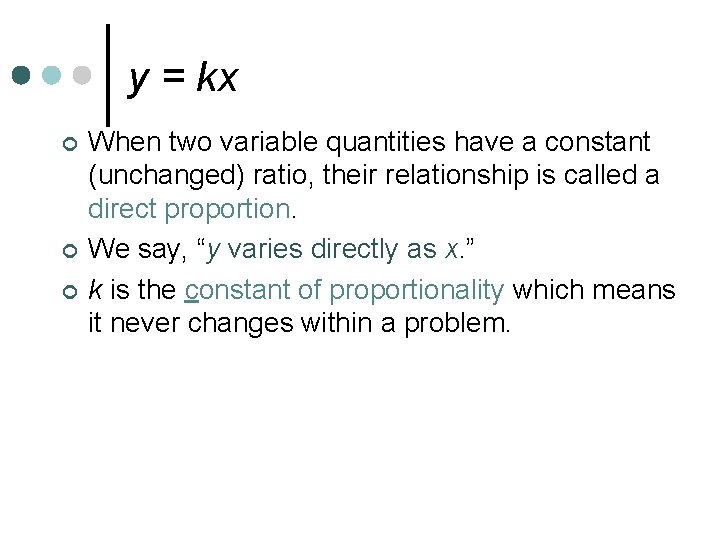







- Slides: 15

Direct Variation Learn to recognize direct variation and identify the constant of proportionality.

Spiders How many legs does a spider have? ¢ 8 legs ¢ Therefore ¢ 2 spiders have a total of 16 legs l 3 spiders have a total of 24 legs l 4 spiders have a total of 32 legs l And so on. . . l ¢ This type of relationship is called. . .

Direct Variation The relationship between the amount of spiders and how many legs they have can be said to vary directly! ¢ We will be learning about equations, tables, and graphs of direct variations. ¢ Sometimes this is called direct proportion rather than direct variation but it is the same thing. ¢

Direct Variation A direct variation relationship can be represented by a linear equation in the form y = kx, where k is a positive number called the constant of proportionality. ¢ The constant of proportionality can sometimes be referred to as the constant of variation. ¢
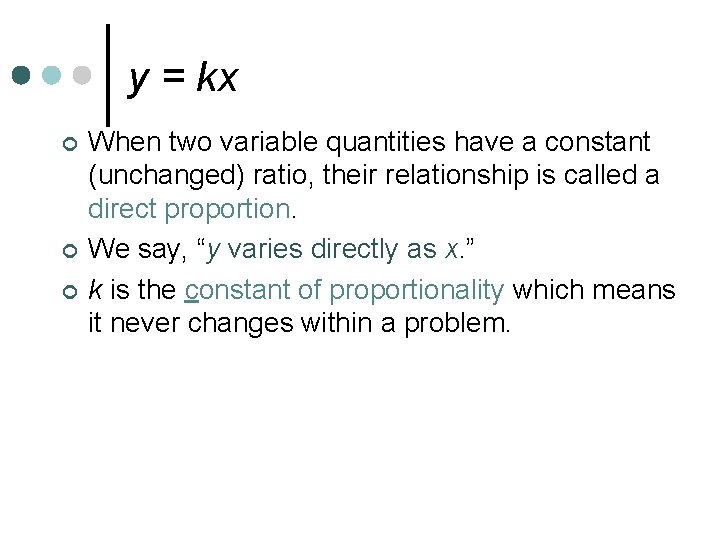
y = kx ¢ ¢ ¢ When two variable quantities have a constant (unchanged) ratio, their relationship is called a direct proportion. We say, “y varies directly as x. ” k is the constant of proportionality which means it never changes within a problem.

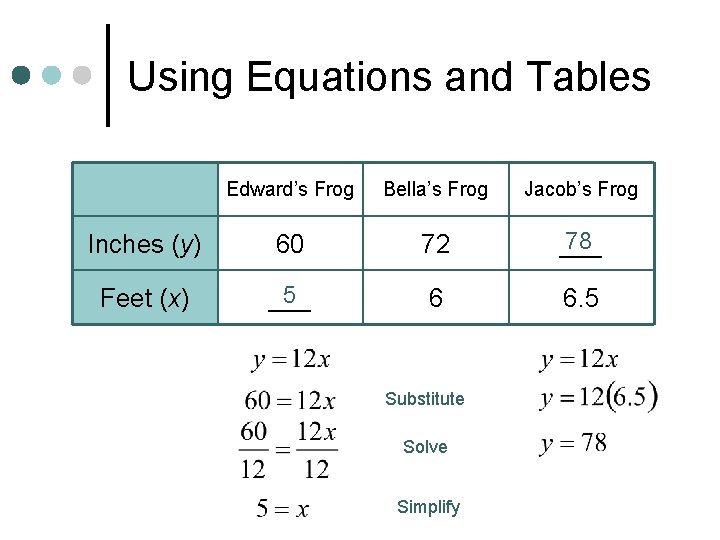
Finding Values Using a Direct Variation Equation ¢ At a frog jumping contest, Edward’s frog jumped 60 inches. Bella’s frog jumped 72 inches. Jacob’s frog jumped 6. 5 feet. Use the equation y = 12 x, where y is the number of inches and x is the number of feet to find the missing values of the table. Edward’s Frog Bella’s Frog Jacob’s Frog Inches (y) 60 72 ___ Feet (x) ___ 6 6. 5

Using Equations and Tables Edward’s Frog Bella’s Frog Jacob’s Frog Inches (y) 60 72 78 ___ Feet (x) 5 ___ 6 6. 5 Substitute Solve Simplify

Now You Try ¢ Identify the constant of proportionality: 1. y = 15 x 15 2. y =. 72 x. 72 3. y = ¼x ¼

How about solving for k? ¢ ¢ ¢ ¢ When we are given the x and y values, we can solve for the constant of proportionality. Example l If y varies directly with x, and y = 8 when x = 12, find k and write an equation that expresses this variation. Steps: 8 = k × 12 Substitute numbers into y = kx 8/12 = (k × 12)/12 Divide both sides by 12 2/3 = k Simplify y = 2/3 x Plug k back into the equation

Now You Try If y varies directly as x, and x = 12 when y = 9, what is the equation that describes this direct variation? ¢ y = kx ¢ 9 = k × 12 ¢ 9/12 = k ¢¾=k ¢ y = ¾x ¢

Now You Try If y varies directly as x, and x = 5 when y = 10, what is the equation that describes this direct variation? ¢ y = kx ¢ 10 = k × 5 ¢ 10/5 = k ¢ 2=k ¢ y = 2 x ¢

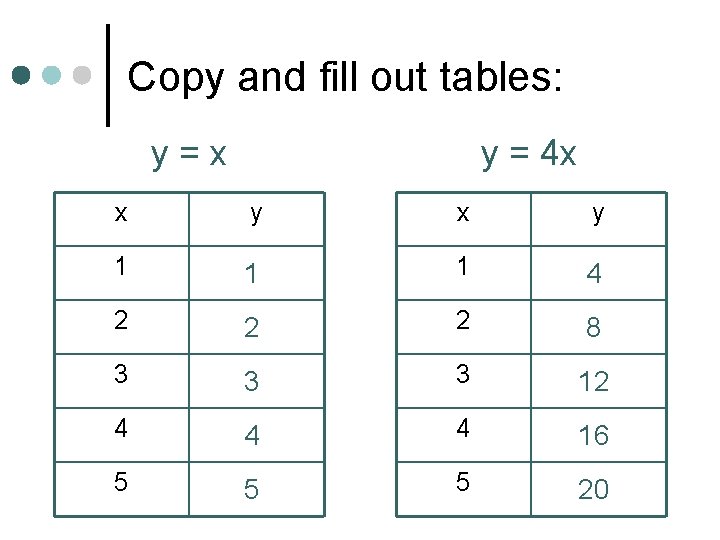
Copy and fill out tables: y=x y = 4 x x y 1 1 1 4 2 2 2 8 3 3 3 12 4 4 4 16 5 5 5 20

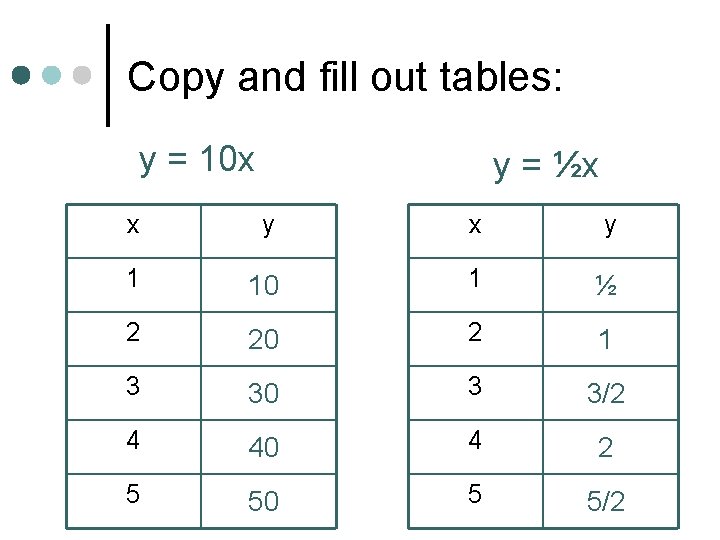
Copy and fill out tables: y = 10 x y = ½x x y 1 10 1 ½ 2 20 2 1 3 30 3 3/2 4 40 4 2 5 50 5 5/2

Direct Variation Equation ¢ ¢ Sometimes we will have to put an equation into y = kx form and solve for y. Then we will be asked to identify k, the constant of proportionality. ¢ ¢ 1. 2. 3. Examples: Tell whether each equation or relationship is a direct variation. If so identify the constant of proportionality. 4 y = 2 x ½y – ¾x = 0 7 y – 5 = 3 x

More Examples ¢ ¢ If y varies directly as x and y = 24 when x = 16, find y when x = 12. Solution: Set up a proportion since the ratios of corresponding values of x to y are always the same.