Direct and Iterative Methods for Sparse Linear Systems

Direct and Iterative Methods for Sparse Linear Systems Shirley Moore svmoore@utep. edu CPS 5401 Fall 2013 svmoore. pbworks. com November 26, 2013 1

Learning Objectives • Describe advantages and disadvantages of direct and iterative methods for solving sparse linear systems. • Describe the general methodology underlying the method of Conjugate Gradients (CG). • Apply appropriate method from a solver library to solve a particular sparse linear system, including both symmetric positive definite and nonsymmetric matrices. • Be able to find and make use of documentation on sparse solver libraries. 2

Direct vs. Iterative Methods • In a direct method, the matrix of the initial linear system is transformed or factorized into a simpler form, which can be solved easily. The exact solution is obtained in a finite number of arithmetic operations, if not considering numerical rounding errors. • Iterative methods compute a sequence of approximate solutions, which converges to the exact solution in the limit, i. e. , in practice until a desired accuracy is obtained. 3

Direct vs. Iterative Methods (cont. ) • Direct methods have been preferred to iterative methods for solving linear systems, mainly because of their simplicity and robustness. • However, the emergence of conjugate gradient methods and Krylov subspace iterations has provided an efficient alternative to direct solvers. • Nowadays, iterative methods are almost mandatory in complex applications, mainly because of memory and computational requirements that prohibit the use of direct methods. • Iterative methods usually involve a matrix-vector multiplication procedure that is cheap to compute on modern computer architectures. • When the matrix A is very large and is composed of a majority of nonzero elements, the LU factorization would contain many more nonzero coefficients than the matrix A itself. • Nonetheless, in some peculiar applications, very ill-conditioned matrices arise that may require a direct method for solving the problem at hand. 4

Direct Solvers for Sparse Linear Systems • Direct solvers for sparse matrices involve much more complicated algorithms than for dense matrices. The main complication is due to the need for efficient handling the fill -in in the factors L and U. A typical sparse solver consists of four distinct steps as opposed to two in the dense case: 1. 2. 3. 4. An ordering step that reorders the rows and columns so that the factors suffer little fill, or so that the matrix has special structure such as block triangular form. An analysis step or symbolic factorization that determines the nonzero structures of the factors and creates suitable data structures for the factors. Numerical factorization that computes the L and U factors. A solve step that performs forward and back substitution using the factors. 5

Direct Solver Packages • Super. LU – http: //crd-legacy. lbl. gov/~xiaoye/Super. LU/ – Super. LU for sequential machines – Super. LU_MT for shared memory parallel machines – Super. LU_DIST for distributed memory parallel machines • See survey of direct solvers by Xiaoye Li – http: //crdlegacy. lbl. gov/~xiaoye/Super. LU/Sparse. Direct. Survey. p df • See also research by Tim Davis – http: //www. cise. ufl. edu/~davis/welcome. html 6

Iterative Methods • Use successive approximations to obtain more accurate solutions to a linear system • Suitable for large sparse linear systems • Stationary methods are older, simple to understand implement, not as effective – Perform same operation each iteration • Nonstationary methods are more recent, harder to understand, highly effective – Have iteration-dependent coefficients • Typically use a transformation matrix called a preconditioner that improves convergence of the method • Reference: Templates book http: //www. netlib. org/linalg/html_templates/report. html 7

Stationary Methods • Jacobi – Based on solving for every variable locally with respect to the other variables – One iteration of the method corresponds to solving for every variable once. – Resulting method is easy to understand implement, but convergence is slow. • Gauss-Seidel – Like the Jacobi method, except that it uses updated values as soon as they are available – In general, if the Jacobi method converges, the Gauss-Seidel method will converge faster than the Jacobi method, though still relatively slowly. • Successive Overrelaxation (SOR) – Can be derived from the Gauss-Seidel method by introducing an extrapolation parameter ω – For the optimal choice of ω, SOR may converge faster than Gauss-Seidel by an order of magnitude. • Symmetric Successive Overrelaxation (SSOR) – No advantage over SOR as a stand-alone iterative method – However, it is useful as a preconditioner for nonstationary methods. 8

Nonstationary Methods • Conjugate Gradient (CG ) – The conjugate gradient method derives its name from the fact that it generates a sequence of conjugate (or orthogonal) vectors. These vectors are the residuals of the iterates. They are also the gradients of a quadratic functional, the minimization of which is equivalent to solving the linear system. CG is an extremely effective method when the coefficient matrix is symmetric positive definite, since storage for only a limited number of vectors is required. • Minimum Residual (MINRES ) and Symmetric LQ (SYMMLQ ) – These methods are computational alternatives for CG for coefficient matrices that are symmetric but possibly indefinite. SYMMLQ will generate the same solution iterates as CG if the coefficient matrix is symmetric positive definite. • Conjugate Gradient on the Normal Equations : CGNE and CGNR – These methods are based on the application of the CG method to one of two forms of the normal equations When the coefficient matrix is nonsymmetric and nonsingular, the normal equations matrices will be symmetric and positive definite, and hence CG can be applied. The convergence may be slow, since the spectrum of the normal equations matrices will be less favorable. 9

Nonstationary Methods (cont. ) • Generalized Minimal Residual (GMRES ) – The Generalized Minimal Residual method computes a sequence of orthogonal vectors (like MINRES), and combines these through a least-squares solve and update. However, unlike MINRES (and CG) it requires storing the whole sequence, so that a large amount of storage is needed. For this reason, restarted versions of this method are used. In restarted versions, computation and storage costs are limited by specifying a fixed number of vectors to be generated. This method is useful for general nonsymmetric matrices. • Bi. Conjugate Gradient (Bi. CG ) – The Biconjugate Gradient method generates two CG-like sequences of vectors, one based on a system with the original coefficient matrix A , and one on AT. Instead of orthogonalizing each sequence, they are made mutually orthogonal, or ``bi-orthogonal''. This method, like CG, uses limited storage. It is useful when the matrix is nonsymmetric and nonsingular; however, convergence may be irregular, and there is a possibility that the method will break down. Bi. CG requires a multiplication with the coefficient matrix and with its transpose at each iteration. • Quasi-Minimal Residual (QMR ) – The Quasi-Minimal Residual method applies a least-squares solve and update to the Bi. CG residuals, thereby smoothing out the irregular convergence behavior of Bi. CG, which may lead to more reliable approximations. In full glory, it has a look ahead strategy built in that avoids the Bi. CG breakdown. Even without look ahead, QMR largely avoids the breakdown that can occur in Bi. CG. On the other hand, it does not effect a true minimization of either the error or the residual, and while it converges smoothly, it often does not improve on the Bi. CG in terms of the number of iteration steps. 10

Nonstationary Methods (cont. ) • Conjugate Gradient Squared (CGS ) – The Conjugate Gradient Squared method is a variant of Bi. CG that applies the updating operations for the A-sequence and the AT-sequences both to the same vectors. Ideally, this would double the convergence rate, but in practice convergence may be much more irregular than for Bi. CG, which may sometimes lead to unreliable results. A practical advantage is that the method does not need the multiplications with the transpose of the coefficient matrix. • Biconjugate Gradient Stabilized (Bi-CGSTAB ) – The Biconjugate Gradient Stabilized method is a variant of Bi. CG, like CGS, but using different updates for the -sequence in order to obtain smoother convergence than CGS. • Chebyshev Iteration – The Chebyshev Iteration recursively determines polynomials with coefficients chosen to minimize the norm of the residual in a min-max sense. The coefficient matrix must be positive definite and knowledge of the extremal eigenvalues is required. This method has the advantage of requiring no inner products. 11

Conjugate Gradient Method • Popular iterative method for solving large systems of sparse linear equations Ax=b • A is known, square, symmetric, positivedefinite • Reference: Shewchuk 12

Quadratic Form • Quadratic form • If A is symmetric and positive-definite, f(x) is minimized by the solution to Ax=b A=AT 13

Method of Steepest Descent • Choose the direction in which f decreases the most: the direction opposite to f’(x(i)) Error Residual as the direction of steepest descent 14

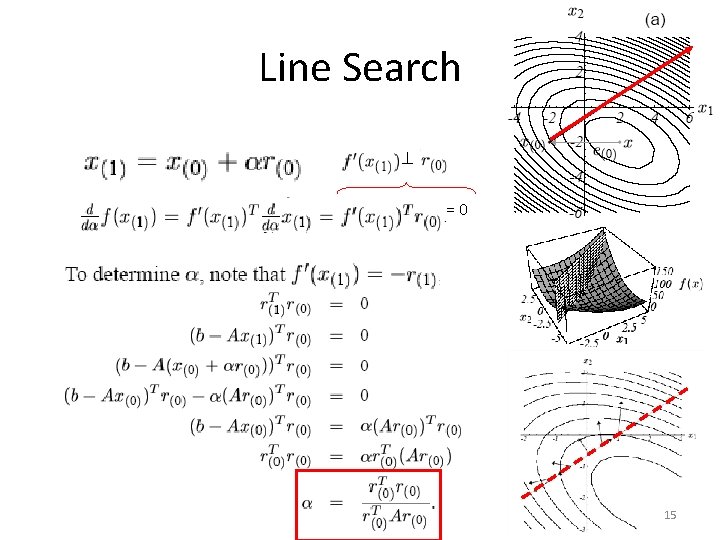
Line Search =0 15

Summary b–A b – A( ) 16

Convergence Analysis • Two cases where one-step convergence is possible – e(i) is the eigenvector (of A) – All eigenvalues of A are the same 17

Convergence Analysis (cont) • In general, depends on condition number of A and the slope of e(0) (relative to coord. system of eigenvectors) at the starting point 18

Method of Conjugate Directions • Idea: Pick a set of n orthogonal directions. In each direction, take exactly one step. After n steps, we’ll be done Algorithm should look like: But we don’t know e(i) ! 19

Conjugate Directions Def: A-orthogonal • Make the search directions {d(i)}A-orthogonal And require A and A-orthogonal Find minimum along d(i) 20

Conjugate Directions • To get stepsize • Algorithm Summary 21

Proof • Can this really solve x in n steps? [since we’ve changed orthogonal to A-orthogonal? ] Intuition: Each step of conjugate directions eliminates one A-orthogonal component of error 22

Initial error represent error in basis of {d(i)} After n iterations, e(n) = 0 23

To find A-orthogonal directions • Conjugate Gram-Schmidt process n linearly independent vectors Difficulty: need to keep all the old search directions to construct the new one! 24

Conjugate Gradients • Conjugate directions where the search directions are constructed by conjugation of the residuals – Setting ui = r(i) – Reasons: residuals are independent, orthogonal to previous search directions, … 25

Method of Conjugate Gradients • Each new residual is orthogonal to all the previous residuals and search directions. • Each new search direction is constructed to be A-orthogonal to all the previous residuals and search directions. • d(2) is a linear combination of r(2) and d(1). Krylov subspace 26

Reduction of Space Complexity Let 27

Convergence Analysis of Conjugate Gradients • With exact arithmetic, CG is complete after n iterations. • Accumulated roundoff error causes residual to gradually lose accuracy, and cancellation error causes search vectors to lose A-orthogonality. • CG is useful for problems so large that is not feasible to run even n iterations. • CG is quicker if there are duplicated eigenvalues. • CG converges more quickly when eigenvalues are clustered together. 28

Convergence Analysis of Conjugate Gradients (cont. ) • See Appendix C 3 of Shewchuk 29

Time and Space Complexity • Shewchuk, p. 38 30

Preconditioning 31

Transformed Preconditioned Conjugate Gradient Method 32

Untransformed Preconditioned Conjugate Gradient Method 33

History of Conjugate Gradient Method • • • Conjugate Direction methods were probably first presented by Schmidt [14] in 1908, and were independently reinvented by Fox, Huskey, and Wilkinson [7] in 1948. In the early fifties, the method of Conjugate Gradients was discovered independently by Hestenes [10] and Stiefel [15]; shortly thereafter, they jointly published what is considered the seminal reference on CG [11]. Convergence bounds for CG in terms of Chebyshev polynomials were developed by Kaniel [12]. A more thorough analysis of CG convergence is provided by van der Sluis and van der Vorst [16]. CG was popularized as an iterative method for large, sparse matrices by Reid [13] in 1971. CG was generalized to nonlinear problems in 1964 by Fletcher and Reeves [6], based on work by Davidon [4] and Fletcher and Powell [5]. Convergence of nonlinear CG with inexact line searches was analyzed by Daniel [3]. A history and extensive annotated bibliography of CG to the mid-seventies is provided by Golub and O’Leary [9]. Most research since that time has focused on nonsymmetric systems. 34

Templates section on Conjugate Gradient Method • http: //www. netlib. org/linalg/html_templates/ node 20. html 35

MATLAB Preconditioned Conjugate Gradients Method • http: //www. mathworks. com/help/matlab/ref /pcg. html 36

Generalized Minimal Residual (GMRES) Method • Generalizes MINRES to unsymmetric systems • Templates book: – http: //www. netlib. org/linalg/html_templates/nod e 29. html 37

MATLAB documentation on GMRES • http: //www. mathworks. com/help/matlab/ref /gmres. html 38

Iterative Method Packages • Included in PETSc – http: //www. mcs. anl. gov/petsc/ – Sparse linear solvers • http: //www. mcs. anl. gov/petsc/documentation/linearsolvertable. html • ITSOL and p. ARMS – http: //www-users. cs. umn. edu/~saad/software/ • Dongarra’s survey of freely available linear algebra software – http: //www. netlib. org/utk/people/Jack. Dongarra/la-sw. html • Vendor libraries – IBM ESSL/PESSL • http: //publib. boulder. ibm. com/infocenter/clresctr/vxrx/index. jsp? topic=%2 Fc om. ibm. cluster. essl. v 5 r 1. essl 100. doc%2 Fam 501_smsubs. htm – Cray-supported version of PETSc – Numerical Algorithms Group (NAG) • http: //www. nag. com/numeric/FL/decisiontrees. asp 39