Dirac Notation and Spectral decomposition Michele Mosca review

Dirac Notation and Spectral decomposition Michele Mosca

review”: Dirac notation For any vector , we let complex conjugate of. denote , the We denote by the inner product between two vectors and defines a linear function that maps (I. e. to the coefficient of its … it maps any state component)

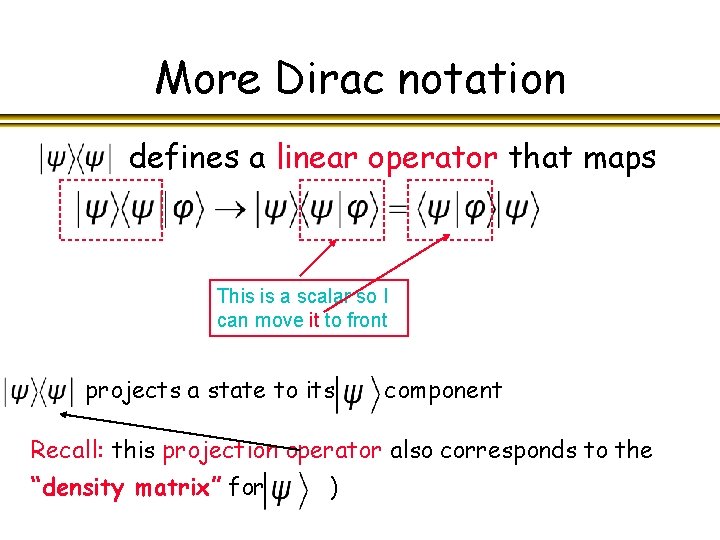
More Dirac notation defines a linear operator that maps This is a scalar so I can move it to front (I. e. projects a state to its component Recall: this projection operator also corresponds to the “density matrix” for )

More Dirac notation More generally, we can also have operators like

Example of this Dirac notation For example, the one qubit NOT gate corresponds to the operator e. g. (sum of matrices applied to ket vector) This is one more notation to calculate state from state and operator The NOT gate is a 1 -qubit unitary operation.

Special unitaries: Pauli Matrices in new notation The NOT operation, is often called the X or σX operation.

Recall: Special unitaries: Pauli Matrices in new representation Representation of unitary operator

What is ? ? It helps to start with the spectral decomposition theorem.

Spectral decomposition l l l Definition: an operator (or matrix) M is t t “normal” if MM =M M t t E. g. Unitary matrices U satisfy UU =U U=I E. g. Density matrices (since they satisfy = t; i. e. “Hermitian”) are also normal Remember: Unitary matrix operators and density matrices are normal so can be decomposed

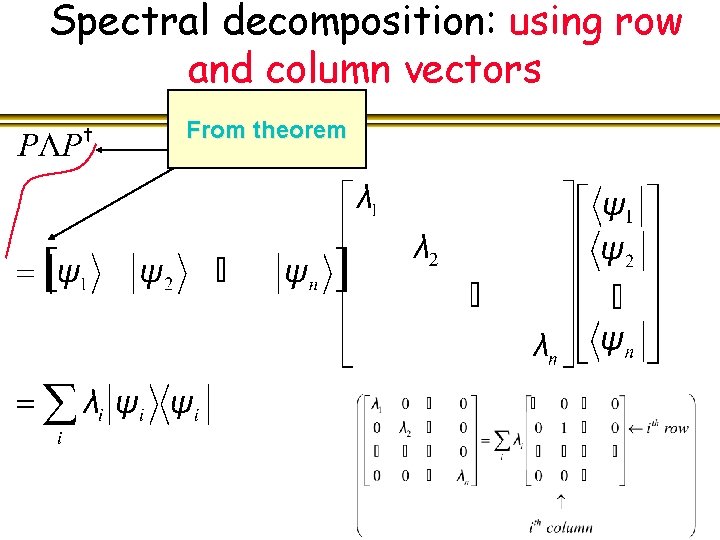
Spectral decomposition Theorem l Theorem: For any normal matrix M, there is a unitary matrix P so that M=P Pt where is a diagonal matrix. The diagonal entries of are the eigenvalues. l The columns of P encode the eigenvectors. l

Example: Spectral decomposition of the NOT gate This is the middle matrix in above decomposition

Spectral decomposition: matrix from column vectors Column vectors

Spectral decomposition: eigenvalues on diagonal Eigenvalues on the diagonal

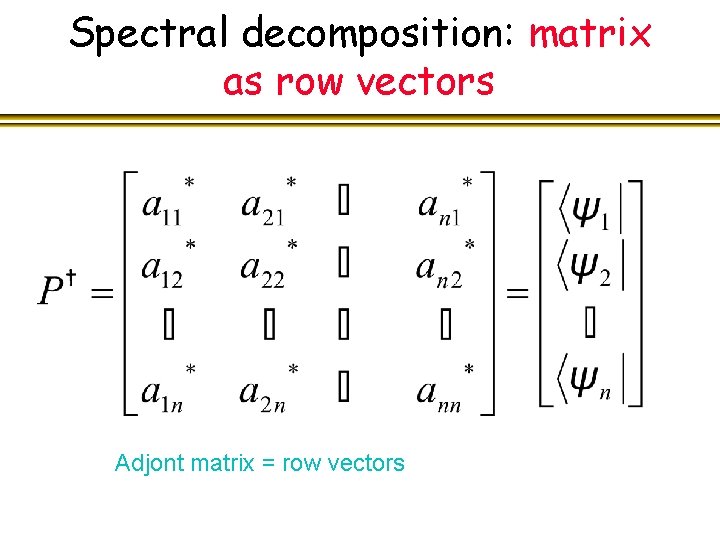
Spectral decomposition: matrix as row vectors Adjont matrix = row vectors

Spectral decomposition: using row and column vectors From theorem

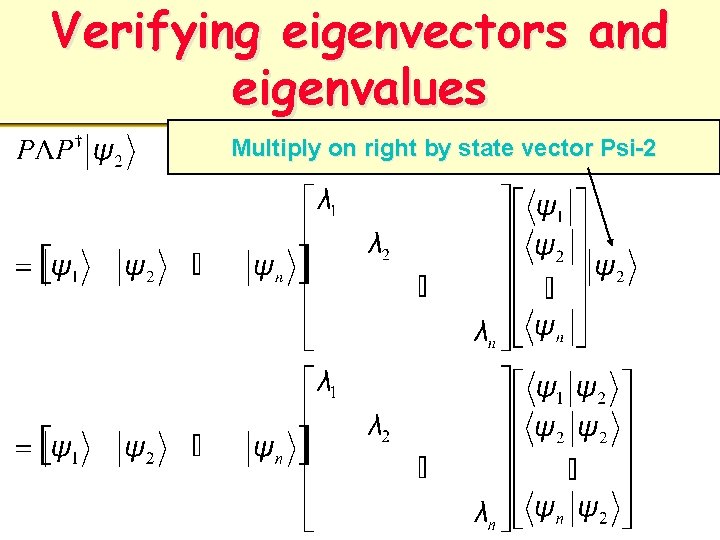
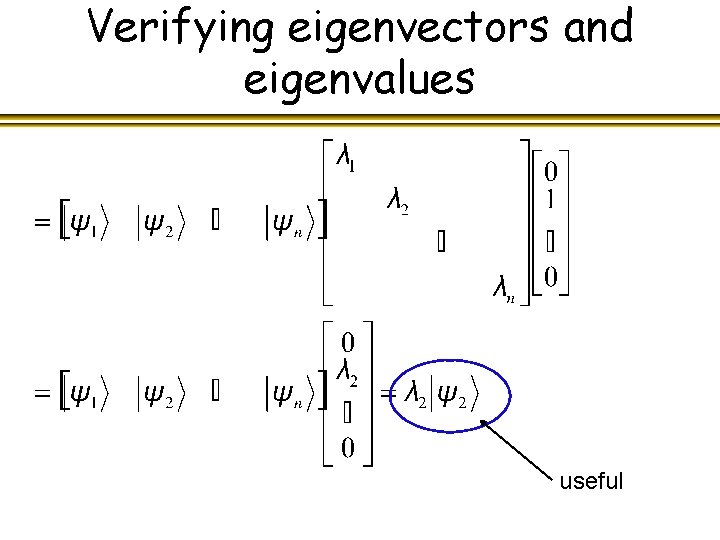
Verifying eigenvectors and eigenvalues Multiply on right by state vector Psi-2

Verifying eigenvectors and eigenvalues useful

Why is spectral decomposition useful? Because we can calculate f(A) m-th power Note that recall So Consider e. g.

Why is spectral decomposition useful? Continue last slide M = f( i)

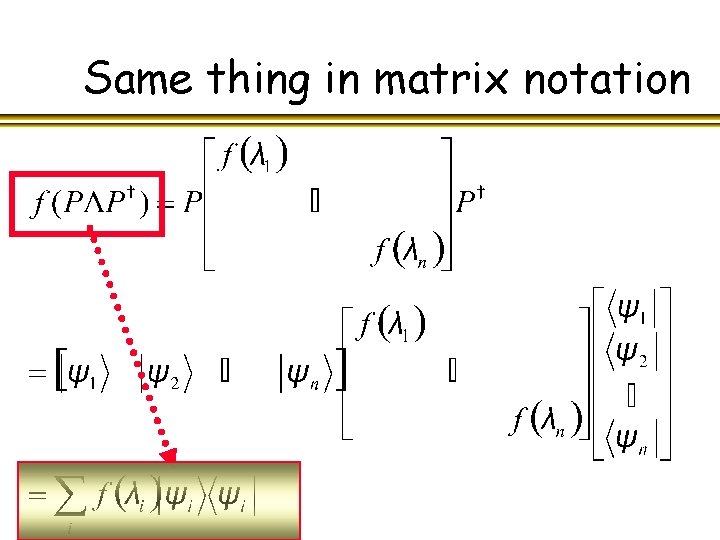
Now f(M) will be in matrix notation

Same thing in matrix notation

Same thing in matrix notation

Important formula in matrix notation

“Von Neumann measurement in the computational basis” l l Suppose we have a universal set of quantum gates, and the ability to measure each qubit in the basis If we measure with probability we get We knew it from beginning but now we can generalize

Using new notation this can be described like this: l We have the projection operators and satisfying We consider the projection operator or “observable” l Note that 0 and 1 are the eigenvalues l l When we measure this observable M, the probability of getting the eigenvalue b is and we are in that case left with the state

Polar Decomposition Left polar decomposition Right polar decomposition This is for square matrices

Gram-Schmidt Orthogonalization Hilbert Space: Orthogonality: Norm: Orthonormal basis: