Dimostrazione di Bohr del modello atomico di H

Dimostrazione di Bohr del modello atomico di H

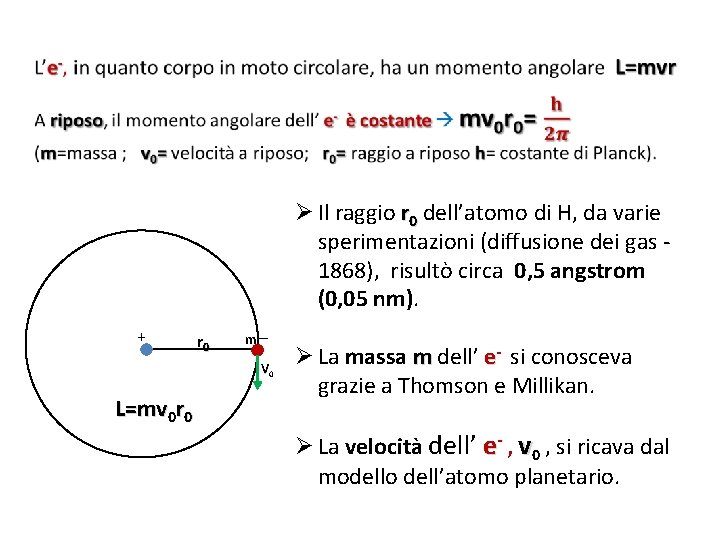
Ø Il raggio r 0 dell’atomo di H, da varie sperimentazioni (diffusione dei gas 1868), risultò circa 0, 5 angstrom (0, 05 nm). + r 0 m _ V 0 L=mv 0 r 0 Ø La massa m dell’ e- si conosceva grazie a Thomson e Millikan. Ø La velocità dell’ e- , v 0 , si ricava dal modello dell’atomo planetario.

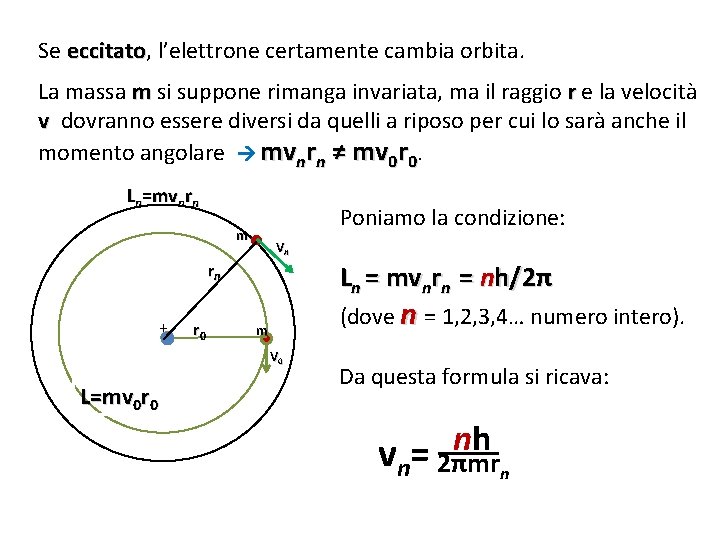
Se eccitato, eccitato l’elettrone certamente cambia orbita. La massa m si suppone rimanga invariata, ma il raggio r e la velocità v dovranno essere diversi da quelli a riposo per cui lo sarà anche il momento angolare mvnrn ≠ mv 0 r 0. Ln=mvnrn Poniamo la condizione: m Vn rn + r 0 Ln = mvnrn = nh/2π (dove n = 1, 2, 3, 4… numero intero). m V 0 L=mv 0 r 0 Da questa formula si ricava: nh vn= 2πmrn

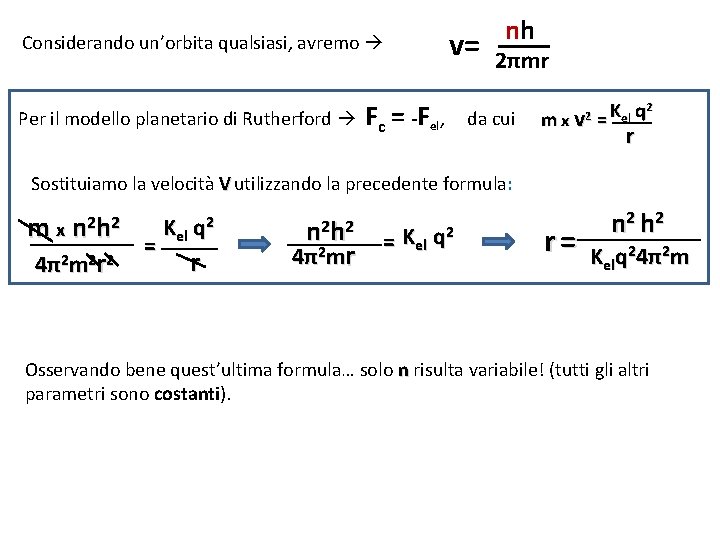
Considerando un’orbita qualsiasi, avremo Per il modello planetario di Rutherford v= Fc = -Fel, nh 2πmr da cui mxv 2 2 K q el = r Sostituiamo la velocità V utilizzando la precedente formula: m x n 2 h 2 r 4 π2 m 2 2 = Kel q 2 r n 2 h 2 r 4 π2 m = Kel q 2 2 r= n 2 h 2 Kelq 24π2 m Osservando bene quest’ultima formula… solo n risulta variabile! (tutti gli altri parametri sono costanti).

La condizione di Bohr e l’equazione di Rydberg Ad ogni orbita corrisponde una specifica energia ET. Considerando due stati, riposo ed eccitato, avremo E 0 ed E 1. Nel cambio di stato avremo una variazione di energia Riprendendo la formula della ET da Rutherford ΔE=E 1 – E 0 2 K q el ET = - ½ r Si avrà… 2 2 K q el el ΔE= E 1 – E 0 = - ½ ½ + r 1 r 0 Sostituiamo r 1 ed r 0 nella formula precedente r= K 2 2 elq 4π m semplificando l’equazione, si arriverà a… ( 2 Kel 2 q 4 m π2 1 1 ΔE= 2 2 n n 2 0 1 h n 2 h 2 )

Ora, dato che si tratta di energia elettromagnetica, sappiamo che il suo valore più piccolo in un segnale è proprio il «quantum» quantum scoperto da Planck ΔE=hf Quindi possiamo porre ΔE= hf = (n 2 Kel 2 q 4 m π2 1 h 2 ( 2 0 - 1 ) n 12 ) 1 h. C = 2 Kel 2 q 4 m π2 1 λ n 02 - n 12 h 2 Portando il fattore h. C a destra… 1 2 Kel 2 q 4 m π2 = λ h 3 C (n 1 2 0 - 1 ) n 12 I valori di Kel, q, m, π, h, C sono noti: possiamo indicarli con una sola lettera R. ( ) 1 =R 1 - 1 n 02 n 12 λ Ma questa è l’equazione empirica di Rydberg per lo spettro dell’idrogeno!