Dimensionality Reduction SVD CUR CS 246 Mining Massive




















![Finding the Principal Eigenvalue � [ ][ ] 1 2 [0. 53 0. 85] Finding the Principal Eigenvalue � [ ][ ] 1 2 [0. 53 0. 85]](https://slidetodoc.com/presentation_image_h2/bab6403febdfaeee19a270a42a5aa608/image-36.jpg)
![Finding More Eigenpairs � [ ] 1 2 M* = 2 3 9/20/2021 [ Finding More Eigenpairs � [ ] 1 2 M* = 2 3 9/20/2021 [](https://slidetodoc.com/presentation_image_h2/bab6403febdfaeee19a270a42a5aa608/image-37.jpg)




















- Slides: 61

Dimensionality Reduction: SVD & CUR CS 246: Mining Massive Datasets Jure Leskovec, Stanford University http: //cs 246. stanford. edu

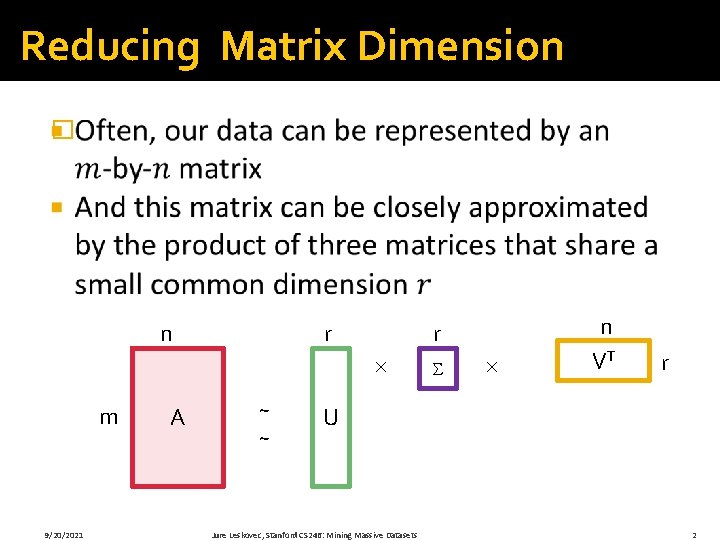
Reducing Matrix Dimension � r n r m 9/20/2021 A ~ ~ n VT r U Jure Leskovec, Stanford CS 246: Mining Massive Datasets 2

Dimensionality Reduction �Compress / reduce dimensionality: § 106 rows; 103 columns; no updates § Random access to any cell(s); small error: OK New representation [1 0] [2 0] [1 0] [5 0] [0 2] [0 3] [0 1] Note: The above matrix is really “ 2 -dimensional. ” All rows can be reconstructed by scaling [1 1 1 0 0] or [0 0 0 1 1] 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 3

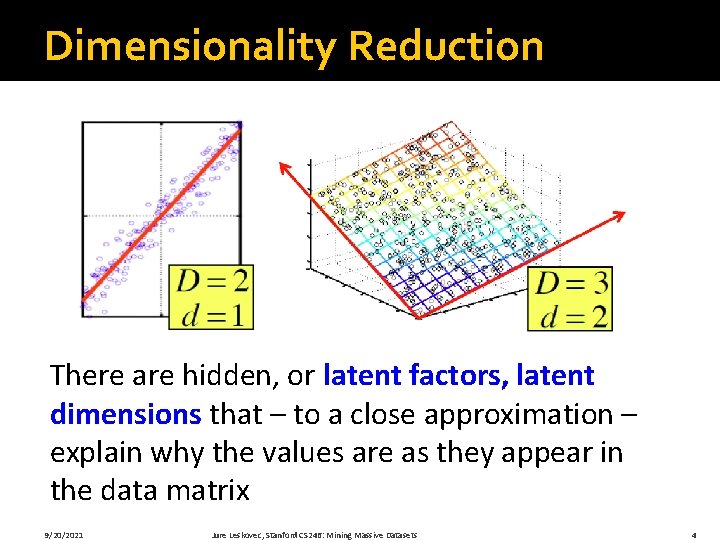
Dimensionality Reduction There are hidden, or latent factors, latent dimensions that – to a close approximation – explain why the values are as they appear in the data matrix 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 4

Dimensionality Reduction The axes of these dimensions can be chosen by: § The first dimension is the direction in which the points exhibit the greatest variance § The second dimension is the direction, orthogonal to the first, in which points show the greatest variance § And so on…, until you have enough dimensions that variance is really low 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 5

Rank is “Dimensionality” �Q: What is rank of a matrix A? �A: Number of linearly independent rows of A �Cloud of points 3 D space: § Think of point positions A as a matrix: 1 row per point: A B C �We can rewrite coordinates more efficiently! § Old basis vectors: [1 0 0] [0 1 0] [0 0 1] § New basis vectors: [1 2 1] [-2 -3 1] § Then A has new coordinates: [1 0], B: [0 1], C: [1 -1] § Notice: We reduced the number of coordinates! 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 6

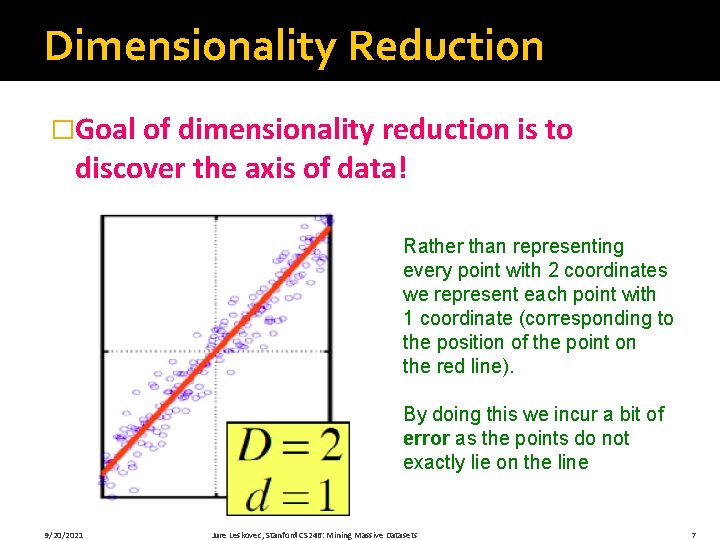
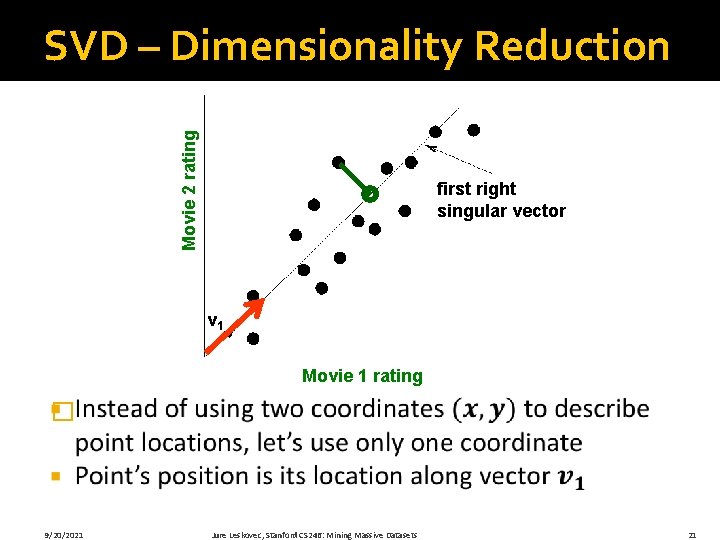
Dimensionality Reduction �Goal of dimensionality reduction is to discover the axis of data! Rather than representing every point with 2 coordinates we represent each point with 1 coordinate (corresponding to the position of the point on the red line). By doing this we incur a bit of error as the points do not exactly lie on the line 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 7

SVD: Singular Value Decomposition

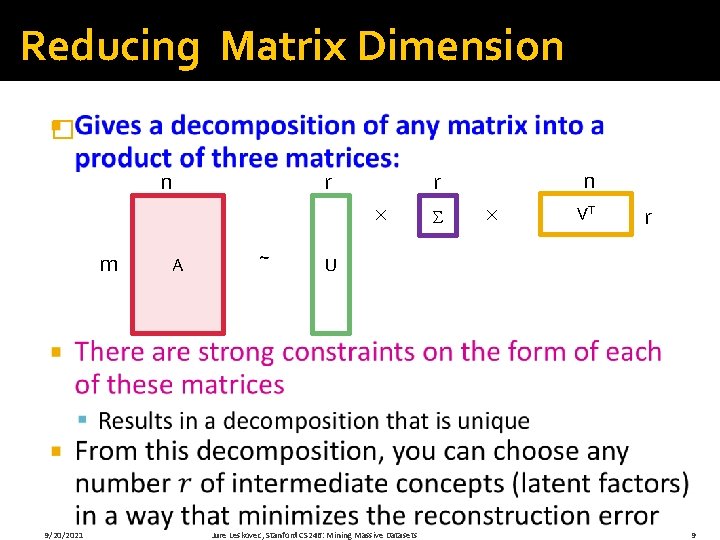
Reducing Matrix Dimension � r n m 9/20/2021 A ~ n r VT r U Jure Leskovec, Stanford CS 246: Mining Massive Datasets 9

SVD - Definition T n r r n r m A m � A: Input data matrix � � � VT U § m x n matrix (e. g. , m documents, n terms) U: Left singular vectors § m x r matrix (m documents, r concepts) : Singular values § r x r diagonal matrix (strength of each ‘concept’) (r : rank of the matrix A) V: Right singular vectors § n x r matrix (n terms, r concepts) 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 10

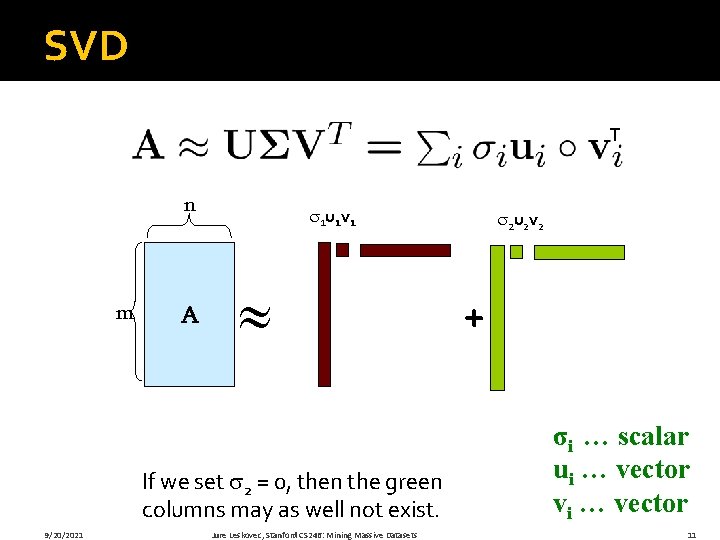
SVD T n m A 1 u 1 v 1 If we set 2 = 0, then the green columns may as well not exist. 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 2 u 2 v 2 + σi … scalar ui … vector vi … vector 11

SVD - Properties It is always possible to decompose a real matrix A into A = U VT , where �U, , V: unique �U, V: column orthonormal § UT U = I; VT V = I (I: identity matrix) § (Columns are orthogonal unit vectors) � : diagonal § Entries (singular values) are positive, and sorted in decreasing order (σ1 σ2 . . . 0) Nice proof of uniqueness: http: //www. mpi-inf. mpg. de/~bast/ir-seminar-ws 04/lecture 2. pdf 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 12

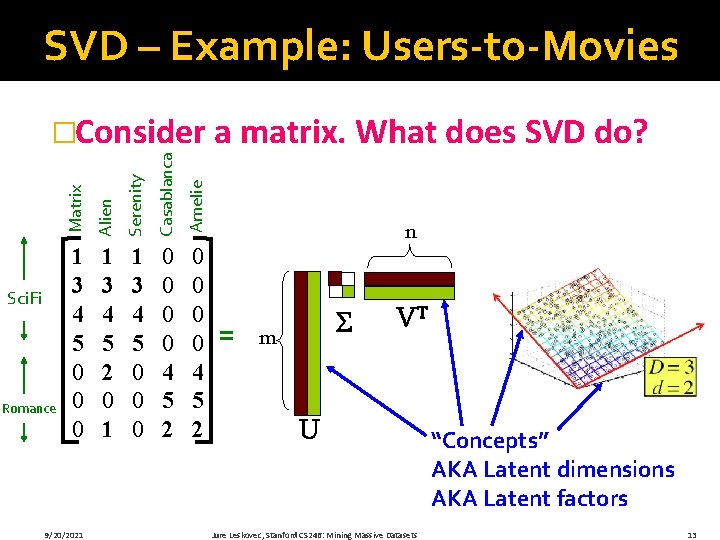
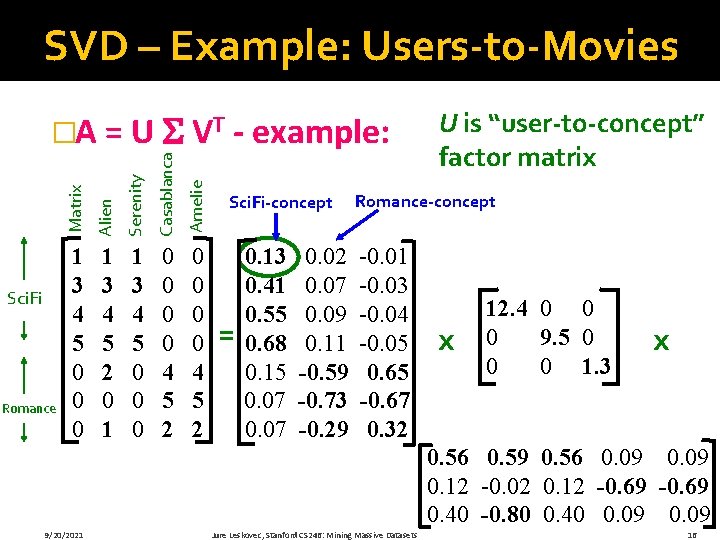
SVD – Example: Users-to-Movies Serenity Casablanca Amelie Romance Alien Sci. Fi Matrix �Consider a matrix. What does SVD do? 1 3 4 5 0 0 0 1 3 4 5 2 0 1 1 3 4 5 0 0 0 0 4 5 2 9/20/2021 n = m VT U Jure Leskovec, Stanford CS 246: Mining Massive Datasets “Concepts” AKA Latent dimensions AKA Latent factors 13

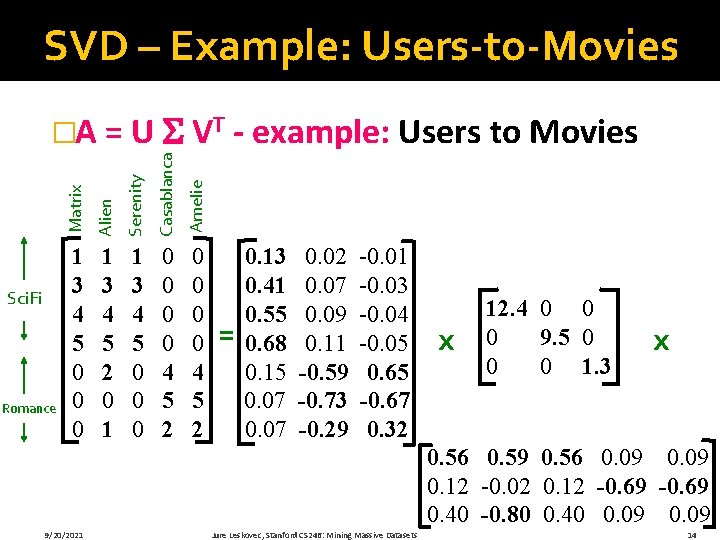
SVD – Example: Users-to-Movies Serenity Casablanca Amelie Romance Alien Sci. Fi Matrix �A = U VT - example: Users to Movies 1 3 4 5 0 0 0 1 3 4 5 2 0 1 1 3 4 5 0 0 0 0 4 5 2 = 0. 13 0. 41 0. 55 0. 68 0. 15 0. 07 0. 02 0. 07 0. 09 0. 11 -0. 59 -0. 73 -0. 29 -0. 01 -0. 03 -0. 04 -0. 05 0. 65 -0. 67 0. 32 x 12. 4 0 0 0 9. 5 0 0 0 1. 3 x 0. 56 0. 59 0. 56 0. 09 0. 12 -0. 02 0. 12 -0. 69 0. 40 -0. 80 0. 40 0. 09 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 14

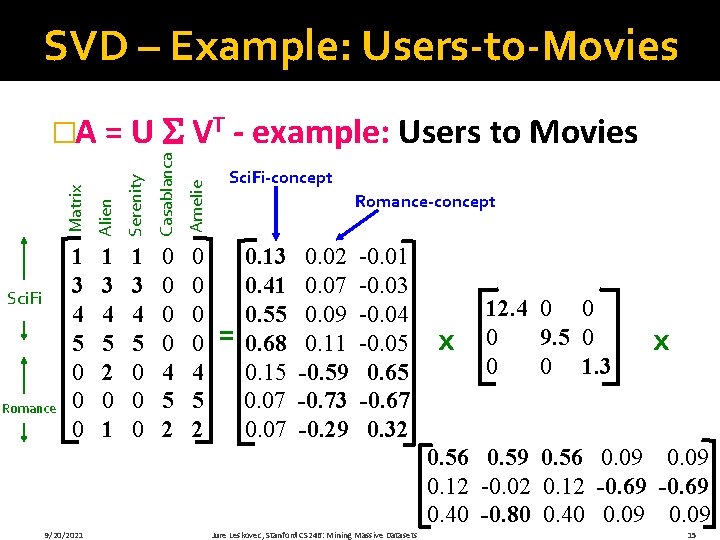
SVD – Example: Users-to-Movies Serenity Casablanca Amelie Romance Alien Sci. Fi Matrix �A = U VT - example: Users to Movies 1 3 4 5 0 0 0 1 3 4 5 2 0 1 1 3 4 5 0 0 0 0 4 5 2 Sci. Fi-concept Romance-concept = 0. 13 0. 41 0. 55 0. 68 0. 15 0. 07 0. 02 0. 07 0. 09 0. 11 -0. 59 -0. 73 -0. 29 -0. 01 -0. 03 -0. 04 -0. 05 0. 65 -0. 67 0. 32 x 12. 4 0 0 0 9. 5 0 0 0 1. 3 x 0. 56 0. 59 0. 56 0. 09 0. 12 -0. 02 0. 12 -0. 69 0. 40 -0. 80 0. 40 0. 09 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 15

SVD – Example: Users-to-Movies Serenity Casablanca Amelie Romance Alien Sci. Fi Matrix �A = U VT - example: 1 3 4 5 0 0 0 1 3 4 5 2 0 1 1 3 4 5 0 0 0 0 4 5 2 Sci. Fi-concept = 0. 13 0. 41 0. 55 0. 68 0. 15 0. 07 0. 02 0. 07 0. 09 0. 11 -0. 59 -0. 73 -0. 29 U is “user-to-concept” factor matrix Romance-concept -0. 01 -0. 03 -0. 04 -0. 05 0. 65 -0. 67 0. 32 x 12. 4 0 0 0 9. 5 0 0 0 1. 3 x 0. 56 0. 59 0. 56 0. 09 0. 12 -0. 02 0. 12 -0. 69 0. 40 -0. 80 0. 40 0. 09 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 16

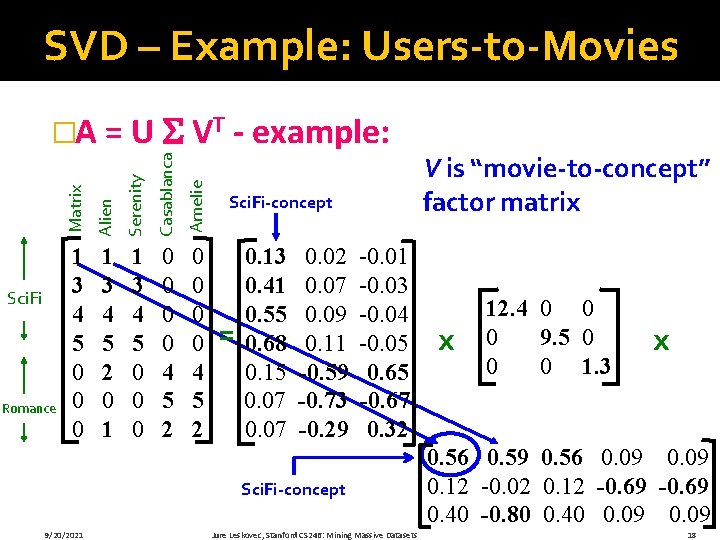
SVD – Example: Users-to-Movies Serenity Casablanca Amelie Romance Alien Sci. Fi Matrix �A = U VT - example: 1 3 4 5 0 0 0 1 3 4 5 2 0 1 1 3 4 5 0 0 0 0 4 5 2 Sci. Fi-concept “strength” of the Sci. Fi-concept = 0. 13 0. 41 0. 55 0. 68 0. 15 0. 07 0. 02 0. 07 0. 09 0. 11 -0. 59 -0. 73 -0. 29 -0. 01 -0. 03 -0. 04 -0. 05 0. 65 -0. 67 0. 32 x 12. 4 0 0 0 9. 5 0 0 0 1. 3 x 0. 56 0. 59 0. 56 0. 09 0. 12 -0. 02 0. 12 -0. 69 0. 40 -0. 80 0. 40 0. 09 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 17

SVD – Example: Users-to-Movies Serenity Casablanca Amelie Romance Alien Sci. Fi Matrix �A = U VT - example: 1 3 4 5 0 0 0 1 3 4 5 2 0 1 1 3 4 5 0 0 0 0 4 5 2 Sci. Fi-concept = 0. 13 0. 41 0. 55 0. 68 0. 15 0. 07 0. 02 0. 07 0. 09 0. 11 -0. 59 -0. 73 -0. 29 -0. 01 -0. 03 -0. 04 -0. 05 0. 65 -0. 67 0. 32 Sci. Fi-concept 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets V is “movie-to-concept” factor matrix x 12. 4 0 0 0 9. 5 0 0 0 1. 3 x 0. 56 0. 59 0. 56 0. 09 0. 12 -0. 02 0. 12 -0. 69 0. 40 -0. 80 0. 40 0. 09 18

SVD - Interpretation #1 ‘movies’, ‘users’ and ‘concepts’: �U: user-to-concept matrix �V: movie-to-concept matrix � : its diagonal elements: ‘strength’ of each concept 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 19

Dimensionality Reduction with SVD

Movie 2 rating SVD – Dimensionality Reduction first right singular vector v 1 Movie 1 rating � 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 21

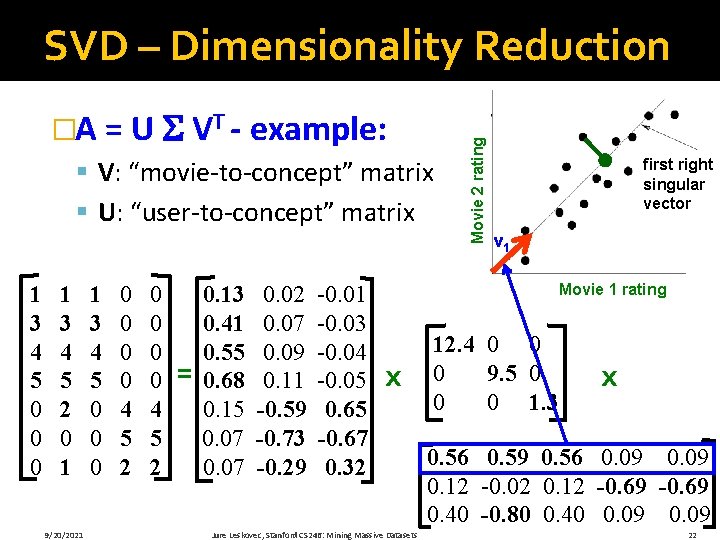
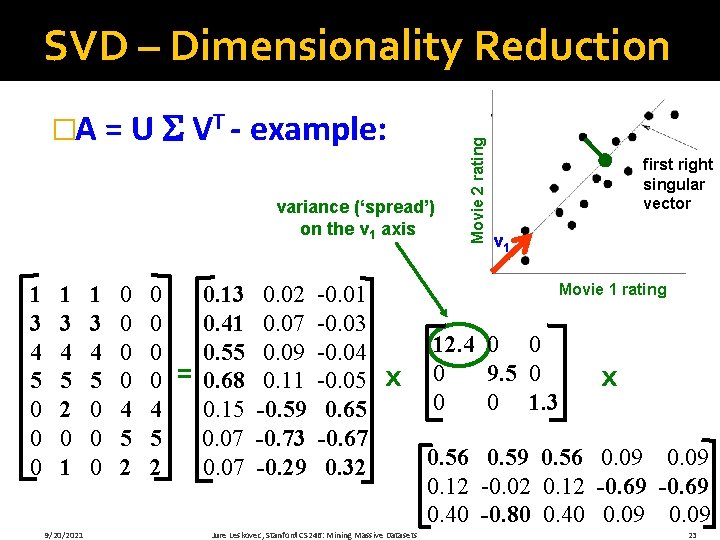
�A = U VT - example: § V: “movie-to-concept” matrix § U: “user-to-concept” matrix 1 3 4 5 0 0 0 1 3 4 5 2 0 1 9/20/2021 1 3 4 5 0 0 0 0 4 5 2 = 0. 13 0. 41 0. 55 0. 68 0. 15 0. 07 0. 02 0. 07 0. 09 0. 11 -0. 59 -0. 73 -0. 29 -0. 01 -0. 03 -0. 04 -0. 05 0. 65 -0. 67 0. 32 Movie 2 rating SVD – Dimensionality Reduction first right singular vector v 1 Movie 1 rating x Jure Leskovec, Stanford CS 246: Mining Massive Datasets 12. 4 0 0 0 9. 5 0 0 0 1. 3 x 0. 56 0. 59 0. 56 0. 09 0. 12 -0. 02 0. 12 -0. 69 0. 40 -0. 80 0. 40 0. 09 22

�A = U VT - example: variance (‘spread’) on the v 1 axis 1 3 4 5 0 0 0 1 3 4 5 2 0 1 9/20/2021 1 3 4 5 0 0 0 0 4 5 2 = 0. 13 0. 41 0. 55 0. 68 0. 15 0. 07 0. 02 0. 07 0. 09 0. 11 -0. 59 -0. 73 -0. 29 -0. 01 -0. 03 -0. 04 -0. 05 0. 65 -0. 67 0. 32 Movie 2 rating SVD – Dimensionality Reduction first right singular vector v 1 Movie 1 rating x Jure Leskovec, Stanford CS 246: Mining Massive Datasets 12. 4 0 0 0 9. 5 0 0 0 1. 3 x 0. 56 0. 59 0. 56 0. 09 0. 12 -0. 02 0. 12 -0. 69 0. 40 -0. 80 0. 40 0. 09 23

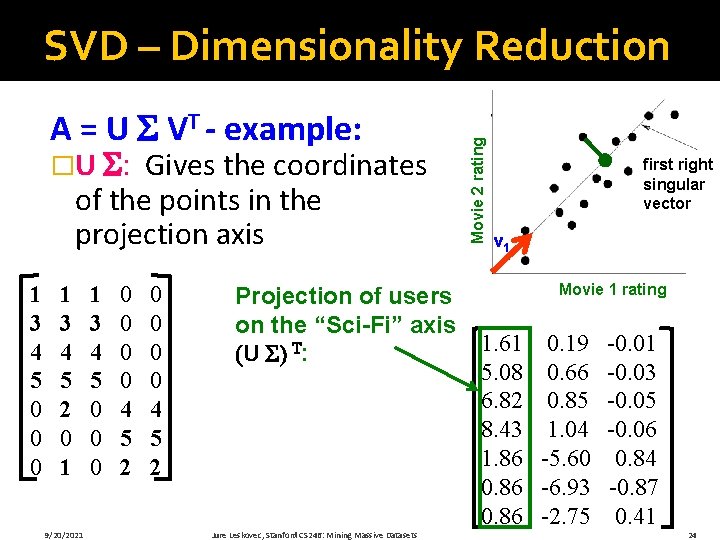
A = U VT - example: �U : Gives the coordinates of the points in the projection axis 1 3 4 5 0 0 0 1 3 4 5 2 0 1 9/20/2021 1 3 4 5 0 0 0 0 4 5 2 Projection of users on the “Sci-Fi” axis (U ) T: Jure Leskovec, Stanford CS 246: Mining Massive Datasets Movie 2 rating SVD – Dimensionality Reduction first right singular vector v 1 Movie 1 rating 1. 61 0. 19 -0. 01 5. 08 0. 66 -0. 03 6. 82 0. 85 -0. 05 8. 43 1. 04 -0. 06 1. 86 -5. 60 0. 84 0. 86 -6. 93 -0. 87 0. 86 -2. 75 0. 41 24

SVD - Interpretation #2 More details �Q: How is dim. reduction done? 1 3 4 5 0 0 0 1 3 4 5 2 0 1 9/20/2021 1 3 4 5 0 0 0 0 4 5 2 = 0. 13 0. 41 0. 55 0. 68 0. 15 0. 07 0. 02 0. 07 0. 09 0. 11 -0. 59 -0. 73 -0. 29 -0. 01 -0. 03 -0. 04 -0. 05 0. 65 -0. 67 0. 32 x Jure Leskovec, Stanford CS 246: Mining Massive Datasets 12. 4 0 0 0 9. 5 0 0 0 1. 3 x 0. 56 0. 59 0. 56 0. 09 0. 12 -0. 02 0. 12 -0. 69 0. 40 -0. 80 0. 40 0. 09 25

SVD - Interpretation #2 More details �Q: How exactly is dim. reduction done? �A: Set smallest singular values to zero 1 3 4 5 0 0 0 1 3 4 5 2 0 1 9/20/2021 1 3 4 5 0 0 0 0 4 5 2 = 0. 13 0. 41 0. 55 0. 68 0. 15 0. 07 0. 02 0. 07 0. 09 0. 11 -0. 59 -0. 73 -0. 29 -0. 01 -0. 03 -0. 04 -0. 05 0. 65 -0. 67 0. 32 x Jure Leskovec, Stanford CS 246: Mining Massive Datasets 12. 4 0 0 0 9. 5 0 0 0 1. 3 x 0. 56 0. 59 0. 56 0. 09 0. 12 -0. 02 0. 12 -0. 69 0. 40 -0. 80 0. 40 0. 09 26

SVD - Interpretation #2 More details �Q: How exactly is dim. reduction done? �A: Set smallest singular values to zero 1 3 4 5 0 0 0 1 3 4 5 2 0 1 9/20/2021 1 3 4 5 0 0 0 0 4 5 2 0. 13 0. 41 0. 55 0. 68 0. 15 0. 07 0. 02 0. 07 0. 09 0. 11 -0. 59 -0. 73 -0. 29 -0. 01 -0. 03 -0. 04 -0. 05 0. 65 -0. 67 0. 32 x Jure Leskovec, Stanford CS 246: Mining Massive Datasets 12. 4 0 0 0 9. 5 0 0 0 1. 3 x 0. 56 0. 59 0. 56 0. 09 0. 12 -0. 02 0. 12 -0. 69 0. 40 -0. 80 0. 40 0. 09 27

SVD - Interpretation #2 This is Rank 2 approximation to A. We could also do Rank 1 approx. The larger the rank the more accurate the approximation. More details �Q: How exactly is dim. reduction done? �A: Set smallest singular values to zero 1 3 4 5 0 0 0 1 3 4 5 2 0 1 9/20/2021 1 3 4 5 0 0 0 0 4 5 2 0. 13 0. 41 0. 55 0. 68 0. 15 0. 07 0. 02 0. 07 0. 09 0. 11 -0. 59 -0. 73 -0. 29 -0. 01 -0. 03 -0. 04 -0. 05 0. 65 -0. 67 0. 32 x Jure Leskovec, Stanford CS 246: Mining Massive Datasets 12. 4 0 0 0 9. 5 0 0 0 1. 3 x 0. 56 0. 59 0. 56 0. 09 0. 12 -0. 02 0. 12 -0. 69 0. 40 -0. 80 0. 40 0. 09 28

SVD - Interpretation #2 This is Rank 2 approximation to A. We could also do Rank 1 approx. The larger the rank the more accurate the approximation. More details �Q: How exactly is dim. reduction done? �A: Set smallest singular values to zero 1 3 4 5 0 0 0 1 3 4 5 2 0 1 9/20/2021 1 3 4 5 0 0 0 0 4 5 2 0. 13 0. 41 0. 55 0. 68 0. 15 0. 07 0. 02 0. 07 0. 09 0. 11 -0. 59 -0. 73 -0. 29 x Jure Leskovec, Stanford CS 246: Mining Massive Datasets 12. 4 0 0 9. 5 x 0. 56 0. 59 0. 56 0. 09 0. 12 -0. 02 0. 12 -0. 69 29

SVD - Interpretation #2 This is Rank 2 approximation to A. We could also do Rank 1 approx. The larger the rank the more accurate the approximation More details �Q: How exactly is dim. reduction done? �A: Set smallest singular values to zero 1 3 4 5 0 0 0 1 3 4 5 2 0 1 1 3 4 5 0 0 0 0 4 5 2 0. 92 2. 91 3. 90 4. 82 0. 70 -0. 69 0. 32 0. 95 3. 01 4. 04 5. 00 0. 53 1. 34 0. 23 0. 92 2. 91 3. 90 4. 82 0. 70 -0. 69 0. 32 Frobenius norm: ǁMǁF = Σij Mij 2 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 0. 01 -0. 01 0. 03 4. 11 4. 78 2. 01 Reconstructed data matrix B ǁA-BǁF = Σij (Aij-Bij)2 is “small” 30

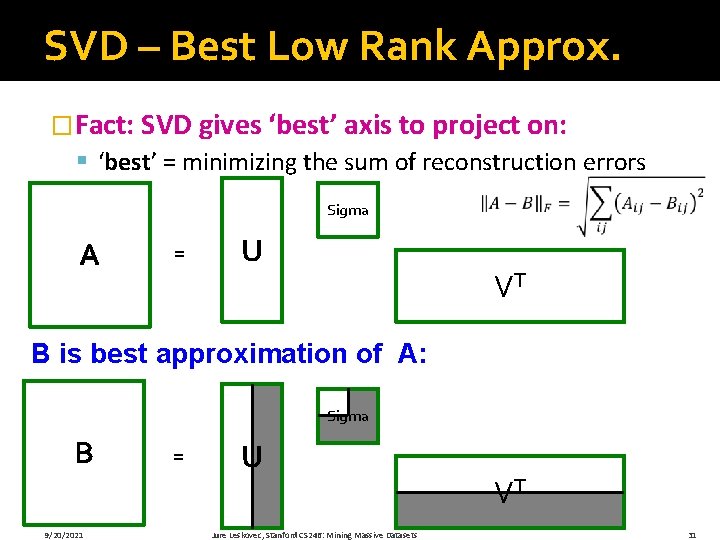
SVD – Best Low Rank Approx. �Fact: SVD gives ‘best’ axis to project on: § ‘best’ = minimizing the sum of reconstruction errors Sigma A = U VT B is best approximation of A: Sigma B 9/20/2021 = U Jure Leskovec, Stanford CS 246: Mining Massive Datasets VT 31

SVD - Conclusions so far � SVD: A= U VT: unique § U: user-to-concept factors § V: movie-to-concept factors § : strength of each concept � Q: So what’s a good value for r? � Let the energy of a set of singular values be the sum of their squares. � Pick r so the retained singular values have at least 90% of the total energy. � Back to our example: § With singular values 12. 4, 9. 5, and 1. 3, total energy = 245. 7 § If we drop 1. 3, whose square is only 1. 7, we are left with energy 244, or over 99% of the total 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 33

How to Compute SVD

Finding Eigenpairs � 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 35

Example: Iterative Eigenvector M= 1 2 2 3 Mx 0 ||Mx 0|| = x 0 = 1 1 0. 51 3 / 34 = 0. 86 5 = x 1 Mx 1 0. 53 2. 23 = = x 2 / 17. 93 = 0. 85 3. 60 ||Mx 1|| …. . 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 36
![Finding the Principal Eigenvalue 1 2 0 53 0 85 Finding the Principal Eigenvalue � [ ][ ] 1 2 [0. 53 0. 85]](https://slidetodoc.com/presentation_image_h2/bab6403febdfaeee19a270a42a5aa608/image-36.jpg)
Finding the Principal Eigenvalue � [ ][ ] 1 2 [0. 53 0. 85] 2 3 9/20/2021 0. 53 0. 85 Jure Leskovec, Stanford CS 246: Mining Massive Datasets = 4. 25 37
![Finding More Eigenpairs 1 2 M 2 3 9202021 Finding More Eigenpairs � [ ] 1 2 M* = 2 3 9/20/2021 [](https://slidetodoc.com/presentation_image_h2/bab6403febdfaeee19a270a42a5aa608/image-37.jpg)
Finding More Eigenpairs � [ ] 1 2 M* = 2 3 9/20/2021 [ ] [ -0. 19 0. 09 0. 53 [0. 53 0. 85] = – 4. 25 0. 09 0. 07 0. 85 Jure Leskovec, Stanford CS 246: Mining Massive Datasets ] 38

How to Compute the SVD � 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 39

Computing the SVD –(2) � 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 40

SVD - Complexity �To compute the full SVD using specialized methods: § O(nm 2) or O(n 2 m) (whichever is less) �But: § Less work, if we just want singular values § or if we want first k singular vectors § or if the matrix is sparse �Implemented in linear algebra packages like § LINPACK, Matlab, SPlus, Mathematica. . . 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 41

Example of SVD

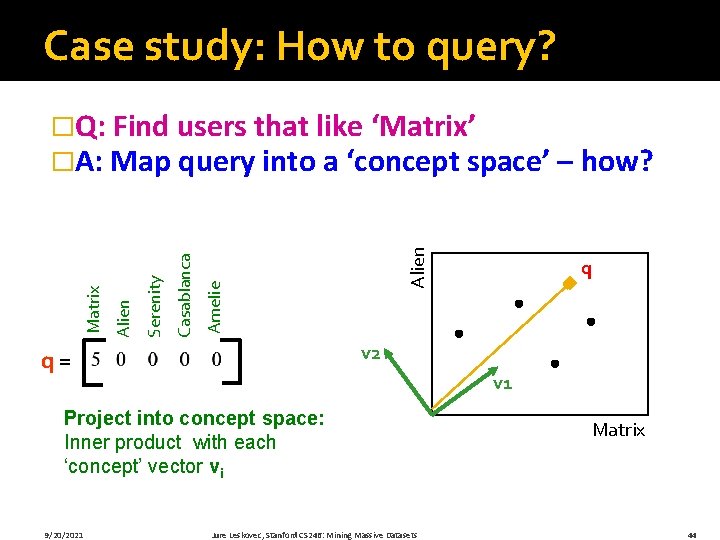
Case study: How to query? Serenity Casablanca Amelie Romnce Alien Sci. Fi Matrix �Q: Find users that like ‘Matrix’ �A: Map query into a ‘concept space’ – how? 1 3 4 5 0 0 0 1 3 4 5 2 0 1 1 3 4 5 0 0 0 0 4 5 2 9/20/2021 = 0. 13 0. 41 0. 55 0. 68 0. 15 0. 07 0. 02 0. 07 0. 09 0. 11 -0. 59 -0. 73 -0. 29 -0. 01 -0. 03 -0. 04 -0. 05 x 0. 65 -0. 67 0. 32 0. 56 0. 12 0. 40 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 12. 4 0 0 0 9. 5 0 0 0 1. 3 x 0. 59 0. 56 0. 09 -0. 02 0. 12 -0. 69 -0. 80 0. 40 0. 09 43

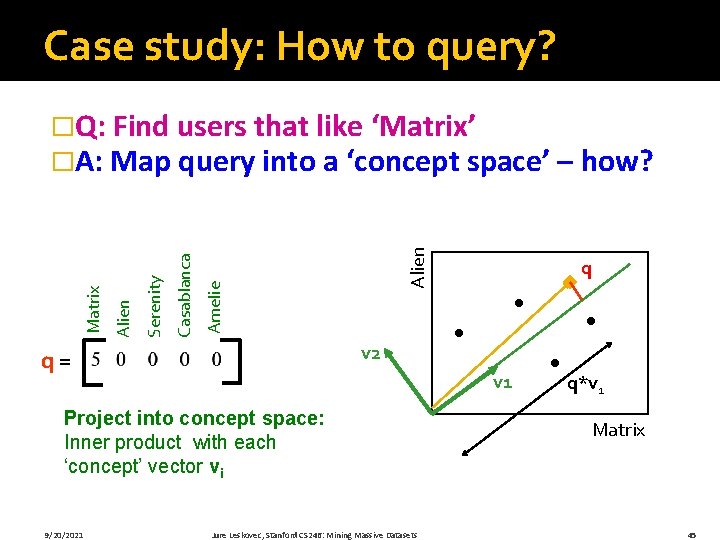
Case study: How to query? Alien Amelie Casablanca Serenity Alien Matrix �Q: Find users that like ‘Matrix’ �A: Map query into a ‘concept space’ – how? v 2 q= v 1 Project into concept space: Inner product with each ‘concept’ vector vi 9/20/2021 q Jure Leskovec, Stanford CS 246: Mining Massive Datasets Matrix 44

Case study: How to query? Alien Amelie Casablanca Serenity Alien Matrix �Q: Find users that like ‘Matrix’ �A: Map query into a ‘concept space’ – how? v 2 q= v 1 Project into concept space: Inner product with each ‘concept’ vector vi 9/20/2021 q Jure Leskovec, Stanford CS 246: Mining Massive Datasets q*v 1 Matrix 45

Case study: How to query? Compactly, we have: qconcept = q V q= Amelie Casablanca Serenity Alien Matrix E. g. : x 0. 56 0. 59 0. 56 0. 09 0. 12 -0. 02 0. 12 -0. 69 Sci. Fi-concept = 2. 8 0. 6 movie-to-concept factors (V) 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 46

Case study: How to query? �How would the user d that rated q= Amelie Casablanca Serenity Alien Matrix (‘Alien’, ‘Serenity’) be handled? dconcept = d V E. g. : x 0. 56 0. 59 0. 56 0. 09 0. 12 -0. 02 0. 12 -0. 69 Sci. Fi-concept = 5. 2 0. 4 movie-to-concept factors (V) 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 47

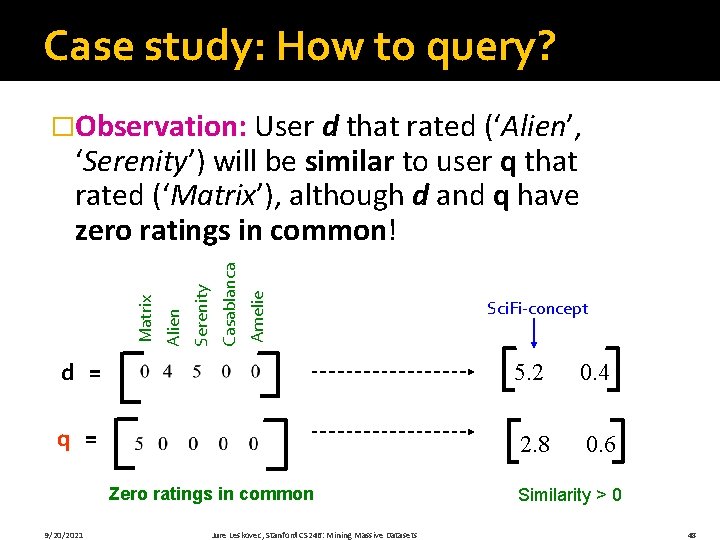
Case study: How to query? �Observation: User d that rated (‘Alien’, Amelie Casablanca Serenity Alien Matrix ‘Serenity’) will be similar to user q that rated (‘Matrix’), although d and q have zero ratings in common! Sci. Fi-concept d = 5. 2 0. 4 q = 2. 8 0. 6 Zero ratings in common 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets Similarity > 0 48

SVD: Drawbacks Optimal low-rank approximation in terms of Frobenius norm - Interpretability problem: + § A singular vector specifies a linear combination of all input columns or rows - Lack of sparsity: § Singular vectors are dense! VT = U 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 49

CUR Decomposition

Sparsity � 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 51

Frobenius norm: CUR Decomposition ǁXǁF = Σij Xij 2 � A 9/20/2021 C Jure Leskovec, Stanford CS 246: Mining Massive Datasets U R 52

Frobenius norm: CUR Decomposition ǁXǁF = Σij Xij 2 � A 9/20/2021 C Jure Leskovec, Stanford CS 246: Mining Massive Datasets U R 53

Computing U � rows, R columns, C A = W intersection 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 54

Which Rows and Columns? � 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 55

CUR: Row Sampling Algorithm �Sampling columns (similarly for rows): Note this is a randomized algorithm, same column can be sampled more than once 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 56

Intuition Actual column Singular vector �Rough and imprecise intuition behind CUR § CUR is more likely to pick points away from the origin § Assuming smooth data with no outliers these are the directions of maximum variation �Example: Assume we have 2 clouds at an angle § SVD dimensions are orthogonal and thus will be in the middle of the two clouds § CUR will find the two clouds (but will be redundant) 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 57

CUR: Provably good approx. to SVD � SVD error CUR error 9/20/2021 In practice: Pick 4 k cols/rows for a “rank-k” approximation Jure Leskovec, Stanford CS 246: Mining Massive Datasets 58

CUR: Pros & Cons + Easy interpretation • Since the basis vectors are actual columns and rows + Sparse basis • Since the basis vectors are actual columns and rows Actual column Singular vector - Duplicate columns and rows • Columns of large norms will be sampled many times 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 59

SVD vs. CUR sparse and small SVD: A = U Huge but sparse T V Big and dense but small CUR: A = C U R Huge but sparse 9/20/2021 Big but sparse Jure Leskovec, Stanford CS 246: Mining Massive Datasets 60

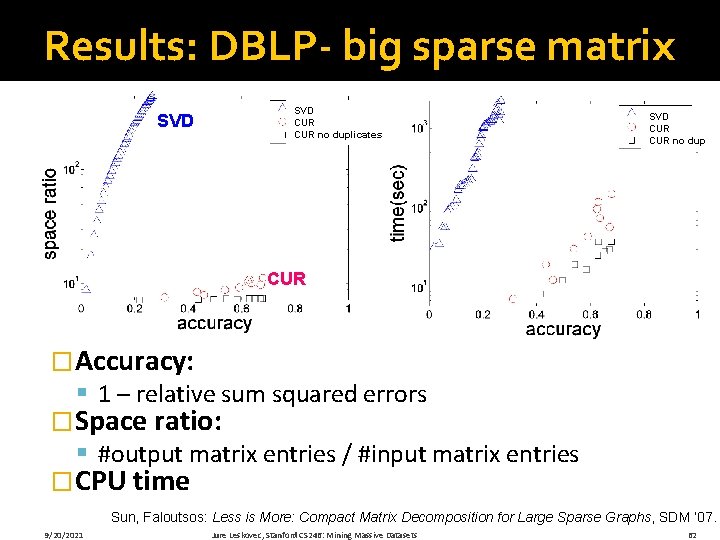
SVD vs. CUR: Simple Experiment �DBLP bibliographic data § Author-to-conference big sparse matrix § Aij: Number of papers published by author i at conference j § 428 K authors (rows), 3659 conferences (columns) § Very sparse �Want to reduce dimensionality § How much time does it take? § What is the reconstruction error? § How much space do we need? 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 61

Results: DBLP- big sparse matrix SVD CUR no duplicates SVD CUR no dup CUR �Accuracy: § 1 – relative sum squared errors �Space ratio: § #output matrix entries / #input matrix entries �CPU time Sun, Faloutsos: Less is More: Compact Matrix Decomposition for Large Sparse Graphs, SDM ’ 07. 9/20/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 62