Dimensionality Reduction by Feature Selection in Machine Learning

Dimensionality Reduction by Feature Selection in Machine Learning Dunja Mladenič J. Stefan Institute, Slovenia

Reasons for dimensionality reduction Dimensionality reduction in machine learning is usually performed to: n n Improve the prediction performance Improve learning efficiency Provide faster predictors possibly requesting less information on the original data Reduce complexity of the learned results, enable better understanding of the underlying process

Approaches to dimensionality reduction Map the original features onto the reduced dimensionality space by: Addressed n selecting a subset of the original features here n n constructing features to replace the original features n n no feature transformation, just select a feature subset using methods from statistics, such as, PCA using background knowledge for constructing new features to be used in addition/instead of the original features (can be followed by feature subset selection) n n general background knowledge (sum or product of features, . . . ) domain specific background knowledge (parser for text data to get noun phrases, clustering of words, user-specified function, …)

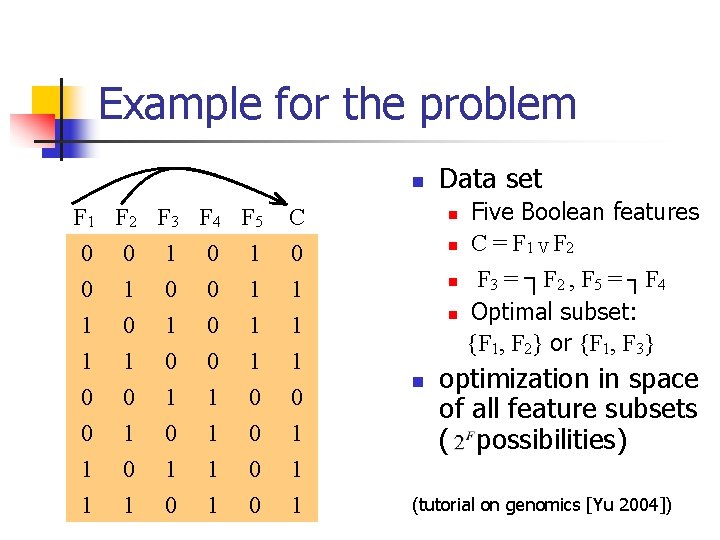
Example for the problem n F 1 F 2 F 3 F 4 F 5 0 0 1 0 1 0 0 1 1 0 0 1 1 1 0 1 0 1 0 0 1 1 1 0 0 C 0 1 1 1 Data set n n n Five Boolean features C = F 1 V F 2 F 3 = ┐F 2 , F 5 = ┐F 4 Optimal subset: {F 1, F 2} or {F 1, F 3} optimization in space of all feature subsets ( possibilities) (tutorial on genomics [Yu 2004])

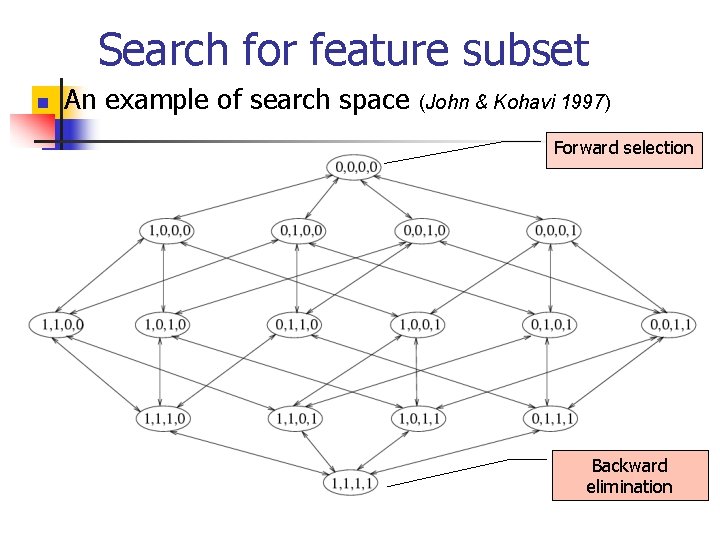
Search for feature subset n An example of search space (John & Kohavi 1997) Forward selection Backward elimination

Feature subset selection n commonly used search strategies: n forward selection n n forward stepwise selection n n FSubset=All. Features; greedily remove features one at a time backward stepwise elimination n n FSubset={}; greedily add or remove features one at a time backward elimination n n FSubset={}; greedily add features one at a time FSubset=All. Features; greedily add or remove features one at a time random mutation n FSubset=Random. Features; greedily add or remove randomly selected feature one at a time stop after a given number of iterations

Approaches to feature subset selection n n Filters - evaluation function independent of the learning algorithm Wrappers - evaluation using model selection based on the machine learning algorithm Embedded approaches - feature selection during learning Simple Filters - assume feature independence (used for problems with large number of features, eg. text classification)

Filtering Evaluation independent of ML algorithm

Filters: Distribution-based [Koller & Sahami 1996] Idea: select a minimal subset of features that keeps class probability distribution close to the original distribution P(C|Feature. Set) is close to P(C|All. Features) 1. 2. n start with all the features use backward elimination to eliminate a predefined number of features evaluation: the next feature to be deleted is obtained using Cross-entropy measure

Filters: Relief [Kira & Rendell 1992] Evaluation of a feature subset 1. represent examples using the feature subset 2. on a random subset of examples calculate average difference in distance from n the nearest example of the same class and the nearest example of the different class n F discrete n some extensions, empirical and theoretical analysis in [Robnik-Sikonja & Kononenko 2003] F cont.

Filters: FOCUS [Almallim & Dietterich 1991] Evaluation of a feature subset 1. 2. n n n represent examples using the feature subset count conflicts in class value (two examples with the same feature values and different class value) Search: all the (promising) subsets of the same (increasing) size are evaluated until a sufficient (no conflicts) subset is found assumes existence of a small sufficient subset --> not appropriate for tasks with many features some extensions of the algorithm use heuristic search to avoid evaluating all the subsets of the same size

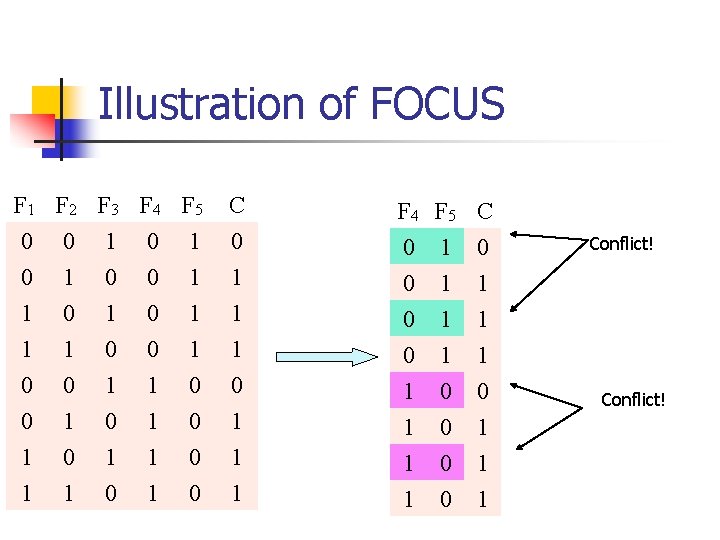
Illustration of FOCUS F 1 F 2 F 3 F 4 F 5 0 0 1 0 1 0 0 1 1 0 0 1 1 1 0 1 0 1 0 0 1 1 1 0 0 C 0 1 1 F 4 0 0 0 F 5 1 1 1 C 0 1 1 1 0 0 1 0 1 1 1 Conflict!

Filters: Random [Liu & Setiono 1996] Evaluation of a feature subset 1. 2. represent examples using the feature subset calculate the inconsistency rate (the average difference between the number of examples with equal feature values and the number of examples among them with the locally, most frequent class value) 3. n n select the smallest subset with inconsistency rate below the given threshold Search: random sampling to search the space of feature subsets evaluate the predetermined number of subsets noise handling by setting the threshold > 0 if threshold = 0, then the same evaluation as in FOCUS

Filters: MDL-based [Pfahringer 1995] Evaluation using Minimum Description Length 1. 2. n n represent examples using the feature subset calculate MDL of a simple decision table representing examples Search: start with random feature subset and add or delete a feature, one at a time performs at least as well as the wrapper approach applied on the simple decision tables and scales up better to large number of training examples

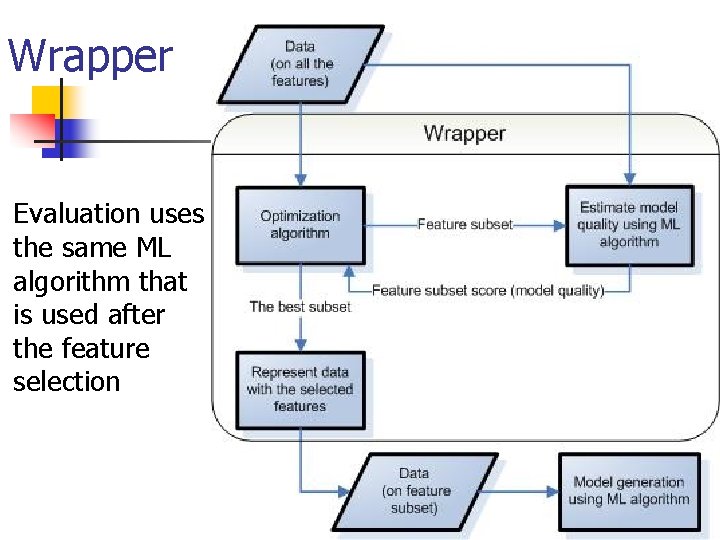
Wrapper Evaluation uses the same ML algorithm that is used after the feature selection

Wrappers: Instance-based learning Evaluation using instance-based learning n represent examples using the feature subset n estimate model quality using cross-validation Search n n n start with random feature subset use beam search with backward elimination Search n n n [Aha & Bankert 1994] [Skalak 1994] start with random feature subset use random mutation

Wrappers: Decision tree induction Evaluation using decision tree induction n represent examples using the feature subset n estimate model quality using cross-validation Search [Bala et al 1995], [Cherkauer & Shavlik 1996] n n using genetic algorithm Search [Caruana & Freitag 1994] n n n adding and removing features (backward stepwise elimination) additionally, at each step removes all the features that were not used in the decision tree induced for the evaluation of the current feature subset

Metric-based model selection Idea: poor models behave differently on training and other data Evaluation using machine learning algorithm represent examples using the feature subset generate model using some ML algorithm estimate model quality comparing the performance of two models on training and on unlabeled data, chose the largest subset that satisfies triangular inequality with all the smaller subsets n n n Combine metric and cross-validation [Bengio & Chapados 2003] n n n based on their disagreement on testing examples (higher disagreement means lower trust to cross-validation) Intuition: cross-validation provides good results but has high variance and should benefit from a combination with model selection having with lower variance

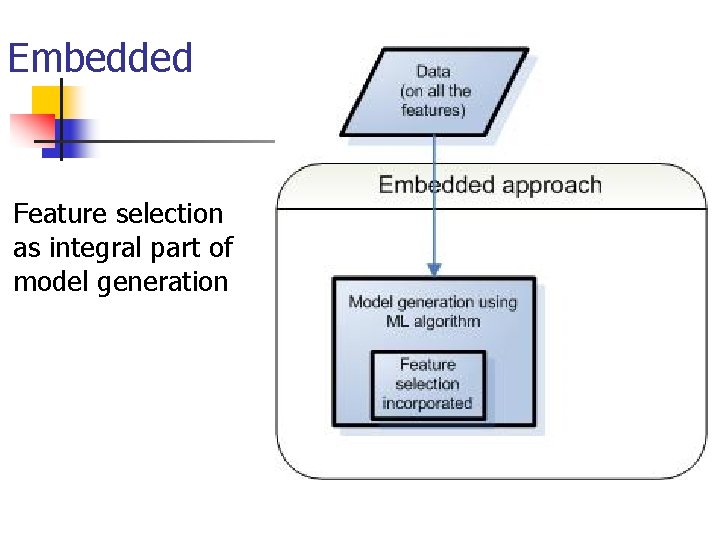
Embedded Feature selection as integral part of model generation

Embedded at each iteration of the incremental optimization of the model n n use a fast gradient-based heuristic to find the most promising feature [Perkins et al 2003] Idea: features that are relevant to the concept should affect the generalization error bound of non-linear SVM more than irrelevant features n n use backward elimination based on the criteria derived from generalization error bounds of the SVM theory (the weight vector norm or, using upper bounds of the leave-one-out error) [Rakotomamonjy 2003]

Embedded: in filters [Cardie 1993] Use embedded feature selection as processing n n n pre- evaluation and search using the process embedded in decision tree induction the final feature subset contains only the features that appear in the induced decision tree used for learning using Nearest Neighbor algorithm

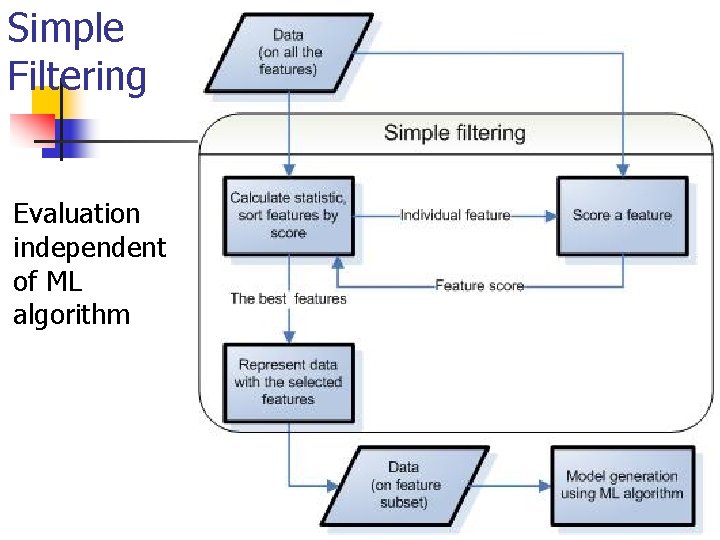
Simple Filtering Evaluation independent of ML algorithm

Feature subset selection on text data – commonly used methods n Simple filtering using some scoring measure to evaluate individual feature n supervised measures: n n supervised measures for binary class n n odds ratio (target class vs. the rest), bi-normal separation unsupervised measures: n n information gain, cross entropy for text (information gain on only one feature value), mutual information for text term frequency, document frequency Simple filtering using embedded approach to score the features n n scoring measure equal to weights in the normal to the hyperplane of linear SVM trained on all the features [Brank et al 2002] learning using linear SVM, Perceptron, Naïve Bayes

Scoring individual feature Information. Gain: n Cross. Entropy. Txt: n Mutual. Info. Txt: n Odds. Ratio: n Frequency: n Bi-Normal. Separation: n F - Normal distribution cumulative probability function

Influence of feature selection on the classification performance n Some ML algorithms are more sensitive to the feature subset than other n n Naïve Bayes on document categorization sensitive to the feature subset Linear SVM has embedded weighting of features that partially compensates for feature selection

Illustration of feature selection n Naïve Bayes on Yahoo! hierarchy data n n Comparison of different feature scoring measures in simple filtering Linear SVM on standard Reuters-2000 news data n Comparison of scoring measures including embedded SVM-normal and perceptron used as pre-processing

Illustration on 5 datasets from Yahoo! hierarchy using Naïve Bayes [Mladenic & Grobelnik 2003]

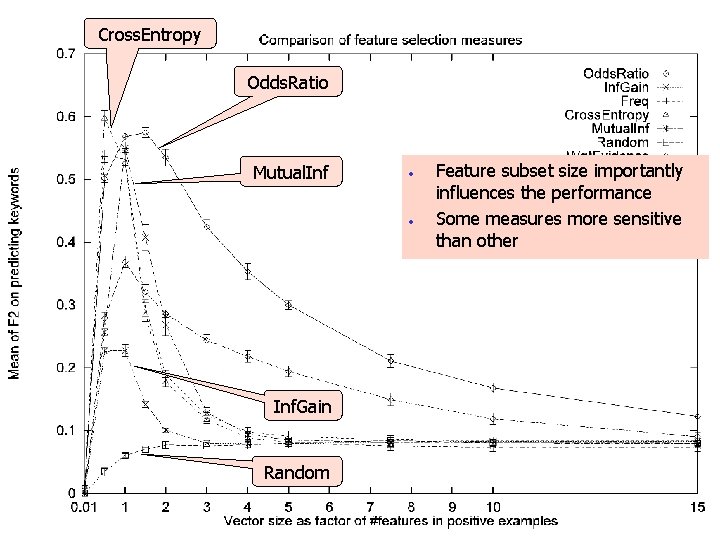
Cross. Entropy Odds. Ratio Mutual. Inf • • Inf. Gain Random Feature subset size importantly influences the performance Some measures more sensitive than other

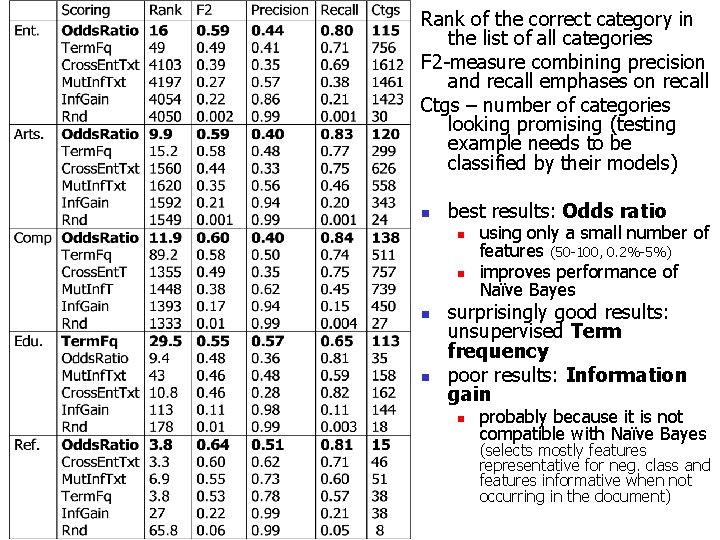
Rank of the correct category in the list of all categories F 2 -measure combining precision and recall emphases on recall Ctgs – number of categories looking promising (testing example needs to be classified by their models) n best results: Odds ratio n n using only a small number of features (50 -100, 0. 2%-5%) improves performance of Naïve Bayes surprisingly good results: unsupervised Term frequency poor results: Information gain n probably because it is not compatible with Naïve Bayes (selects mostly features representative for neg. class and features informative when not occurring in the document)

Illustration on Reuters-2000 Data ~810, 000 News articles 504, 468 articles Training Period 20. Aug, 1996 [Brank et al 2002] 103 Categories 302, 323 articles Test Period 14. April, 1997 19. Aug, 1997 Reuters-2000 Data used in the experiments n n n 16 categories covering the range of break-event point (estimated on a sample) and class distribution Training: sample of 118, 294 articles from the training period Testing: 302, 323 articles from the test period

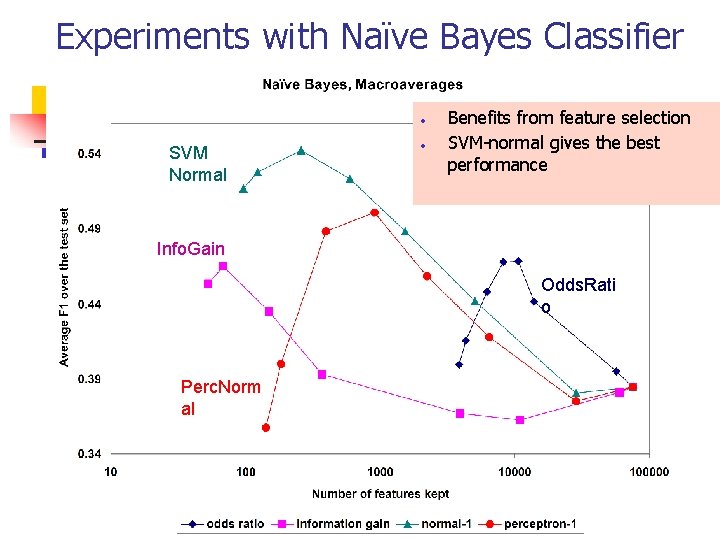
Experiments with Naïve Bayes Classifier • SVM Normal • Benefits from feature selection SVM-normal gives the best performance Info. Gain Odds. Rati o Perc. Norm al

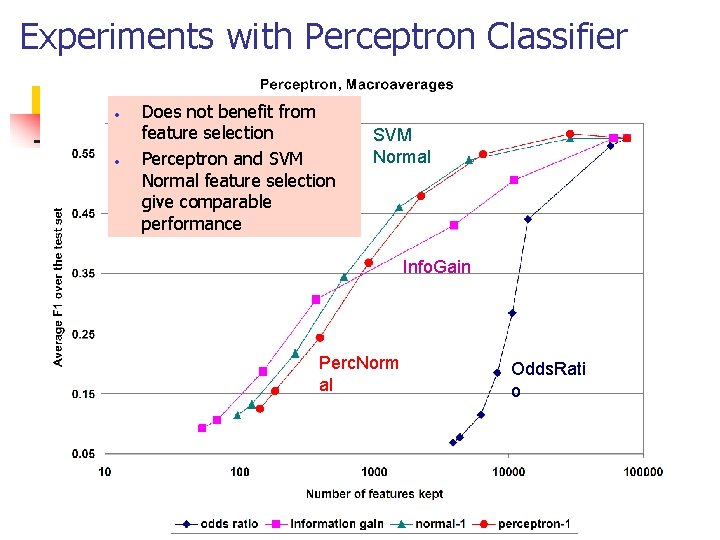
Experiments with Perceptron Classifier • • Does not benefit from feature selection Perceptron and SVM Normal feature selection give comparable performance SVM Normal Info. Gain Perc. Norm al Odds. Rati o

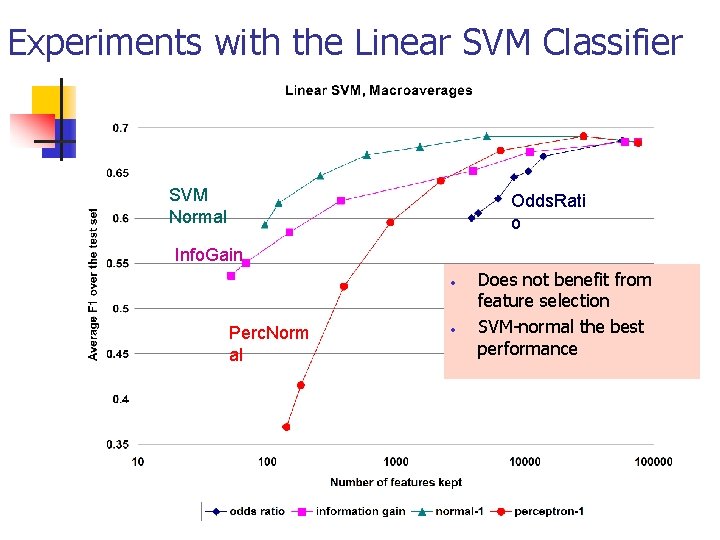
Experiments with the Linear SVM Classifier SVM Normal Odds. Rati o Info. Gain • Perc. Norm al • Does not benefit from feature selection SVM-normal the best performance

Discussion Using discarded features can help The features that harm performance if used as input were found to improve performance if used as additional output n n obtain additional information by introducing mapping from the selected features to the discarded features (the multitask learning setting [Caruana de Sa 2003]) experiments on synthetic regression and classification problems and real -world medical data have shown improvements in performance Intuition: transfer of information occurs inside the model, when in addition to the class value it models also additional output consisting of the discarded features

Discussion Feature subset selection as pre-processing n ignore interaction with the target learning algorithm n n Simple Filters – work for large number of features n assume feature independence, limited results n the size of feature subset to be determined Filters – search space of size n n , can not handle many features relay on general data characteristics (consistency, distance, class distribution) use the target learning algorithm for evaluation n Wrappers – high accuracy, computationally expensive n use model selection with cross-validation of the target algorithm, similar to metric-based model selection (eg. , comparing output on training and on unlabeled data) Feature subset selection during learning n use the target learning algorithm during feature selection n Embedded – can be used by filters to find the feature subset