Dilation a transformation that produces an image that







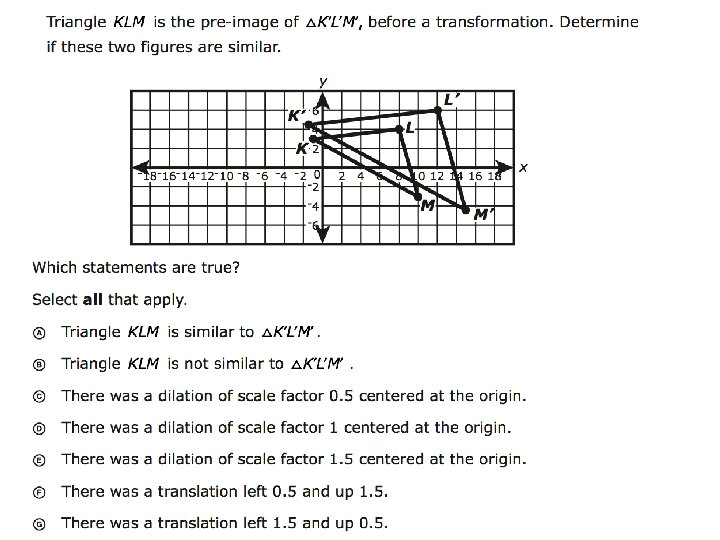


- Slides: 34

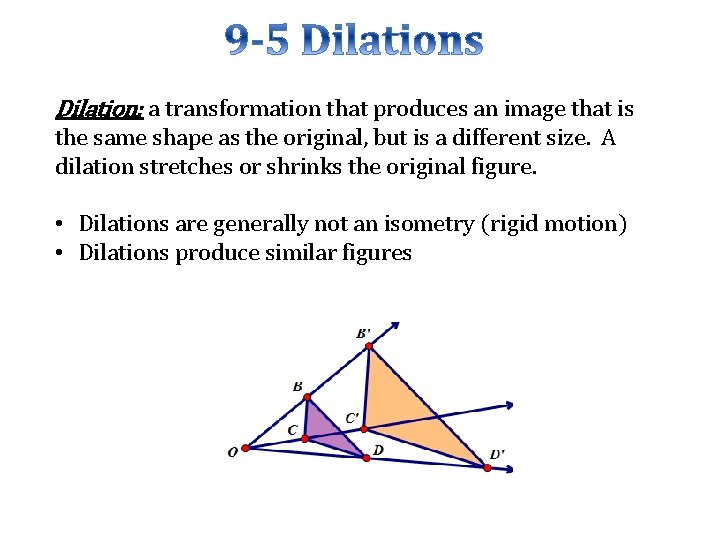
Dilation: a transformation that produces an image that is the same shape as the original, but is a different size. A dilation stretches or shrinks the original figure. • Dilations are generally not an isometry (rigid motion) • Dilations produce similar figures


Scale Factor: measures how much larger or smaller an image is • A scale factor > 1 is an enlargement (figure will become larger) • A scale factor between 0 and 1 is a reduction. (figure will become smaller) The center of dilation is a fixed point in the plane about which all points are expanded or contracted. It is the only point that does not move!

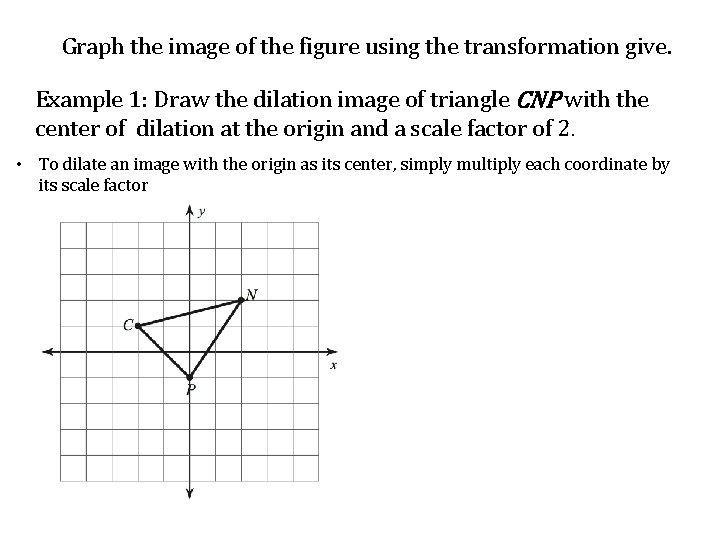
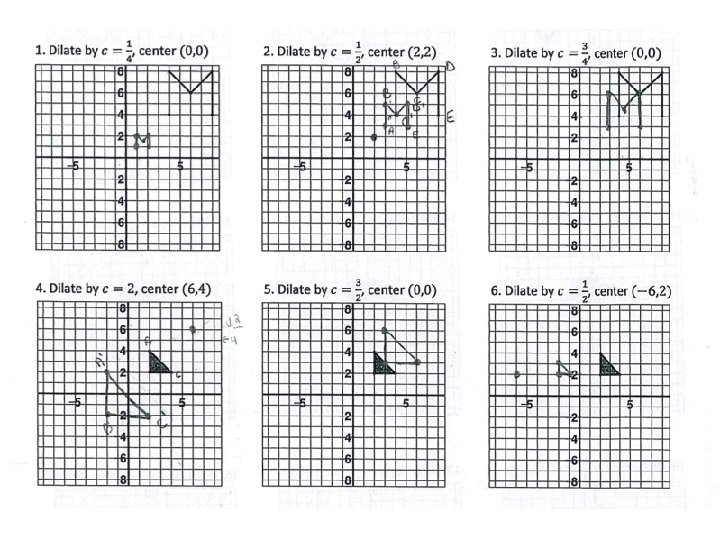
Graph the image of the figure using the transformation give. Example 1: Draw the dilation image of triangle CNP with the center of dilation at the origin and a scale factor of 2. • To dilate an image with the origin as its center, simply multiply each coordinate by its scale factor

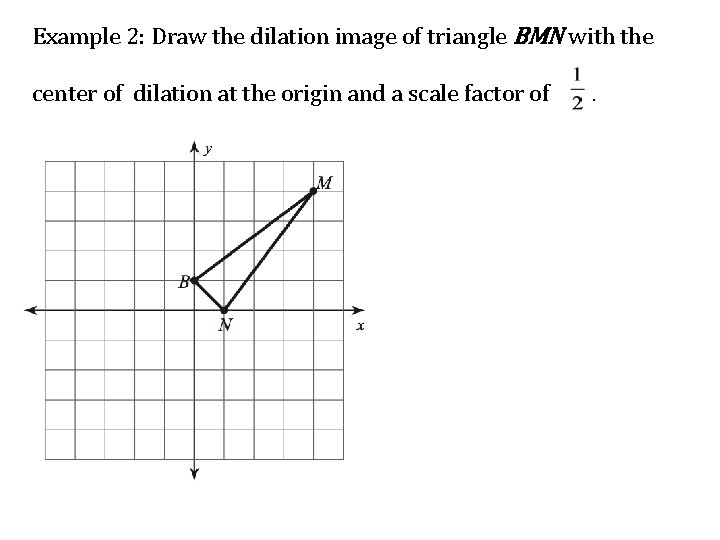
Example 2: Draw the dilation image of triangle BMN with the center of dilation at the origin and a scale factor of .

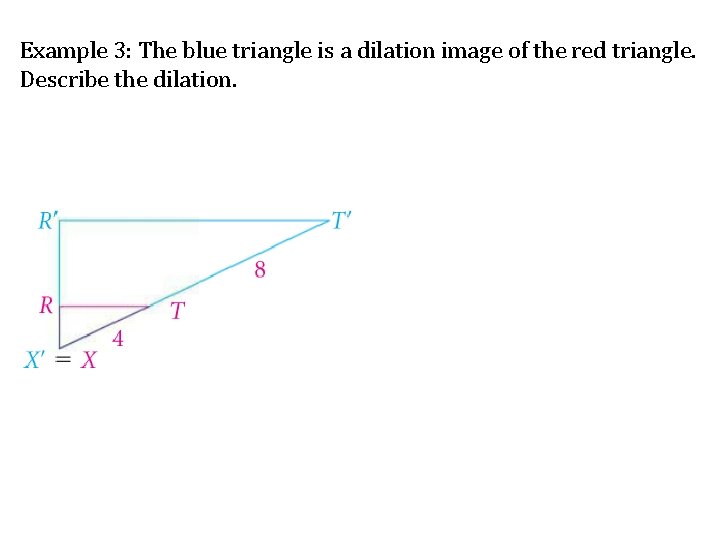
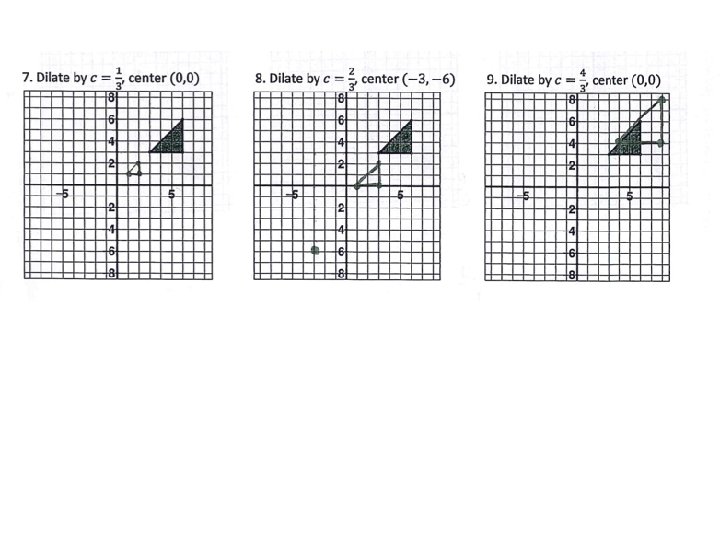
Example 3: The blue triangle is a dilation image of the red triangle. Describe the dilation.

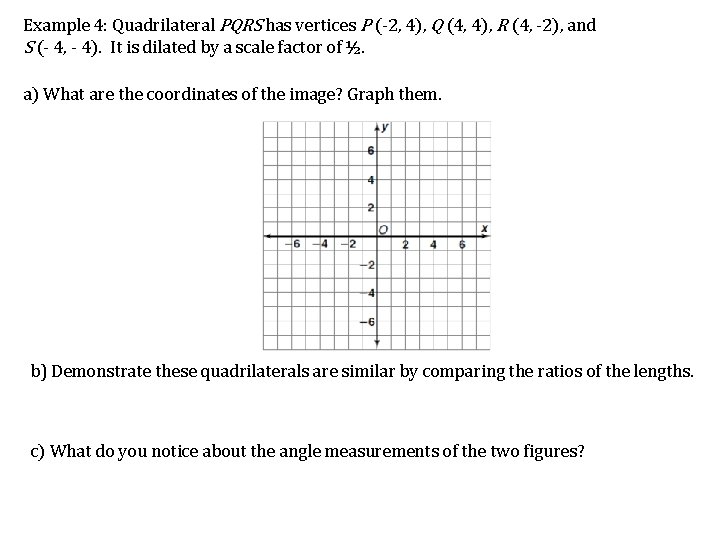
Example 4: Quadrilateral PQRS has vertices P (-2, 4), Q (4, 4), R (4, -2), and S (- 4, - 4). It is dilated by a scale factor of ½. a) What are the coordinates of the image? Graph them. b) Demonstrate these quadrilaterals are similar by comparing the ratios of the lengths. c) What do you notice about the angle measurements of the two figures?








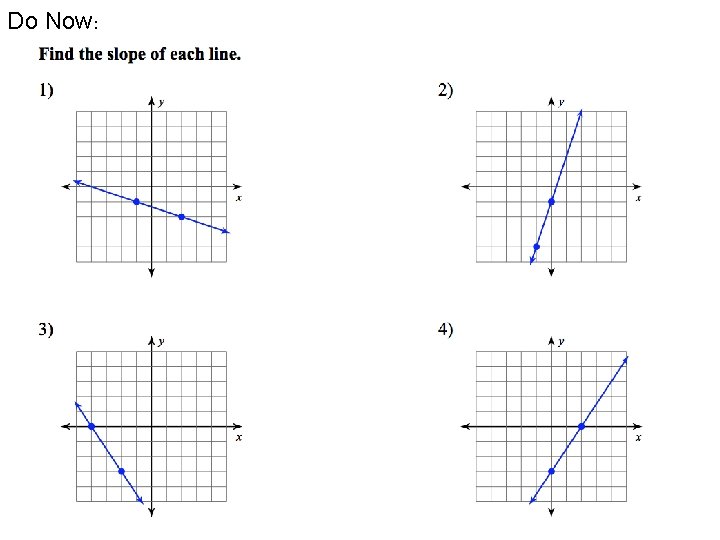
Do Now:


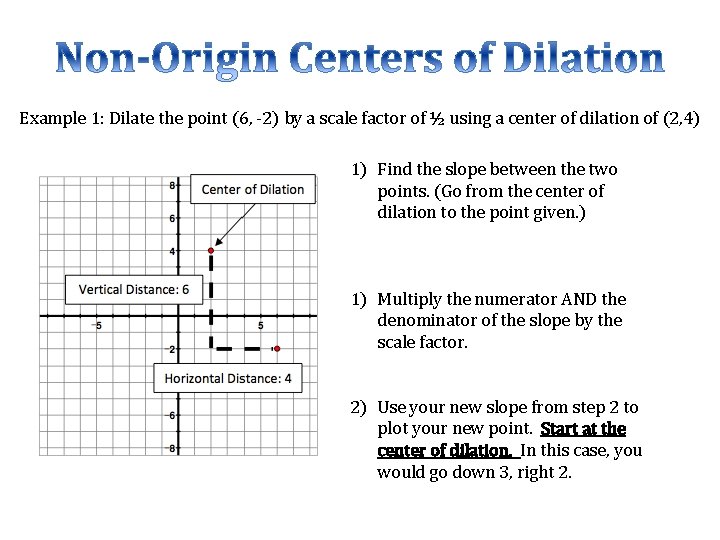
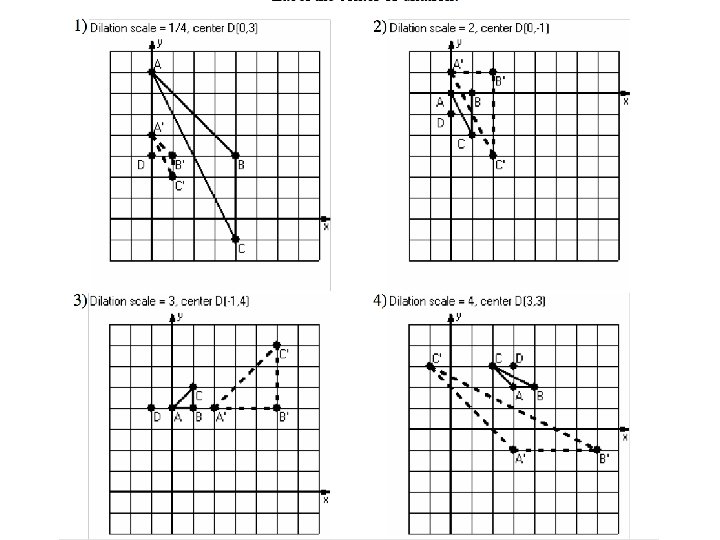
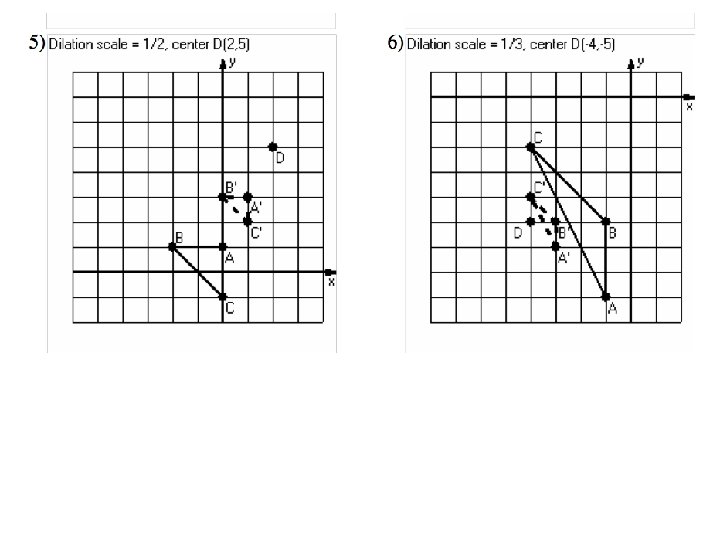
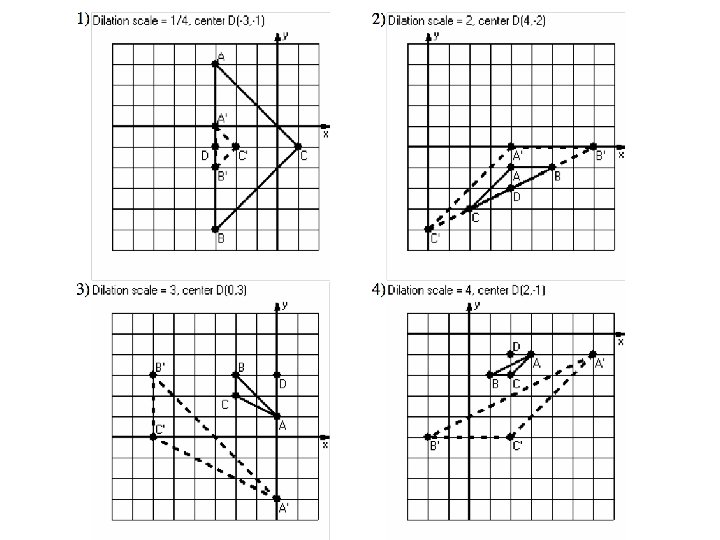
Example 1: Dilate the point (6, -2) by a scale factor of ½ using a center of dilation of (2, 4) 1) Find the slope between the two points. (Go from the center of dilation to the point given. ) 1) Multiply the numerator AND the denominator of the slope by the scale factor. 2) Use your new slope from step 2 to plot your new point. Start at the center of dilation. In this case, you would go down 3, right 2.


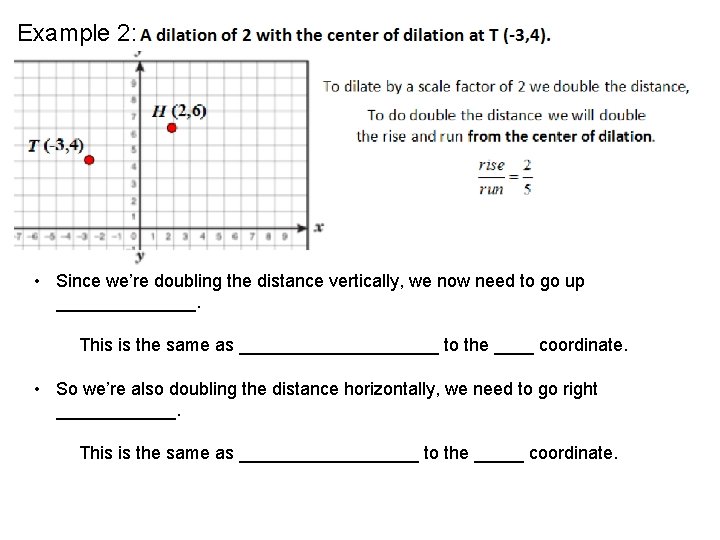
Example 2: • Since we’re doubling the distance vertically, we now need to go up _______. This is the same as __________ to the ____ coordinate. • So we’re also doubling the distance horizontally, we need to go right ______. This is the same as _________ to the _____ coordinate.

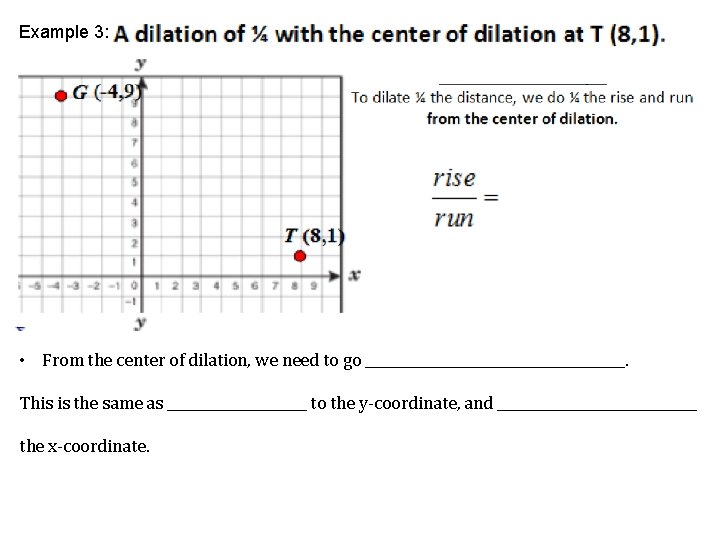
Example 3: • From the center of dilation, we need to go ____________________. This is the same as ___________ to the y-coordinate, and _______________ the x-coordinate.








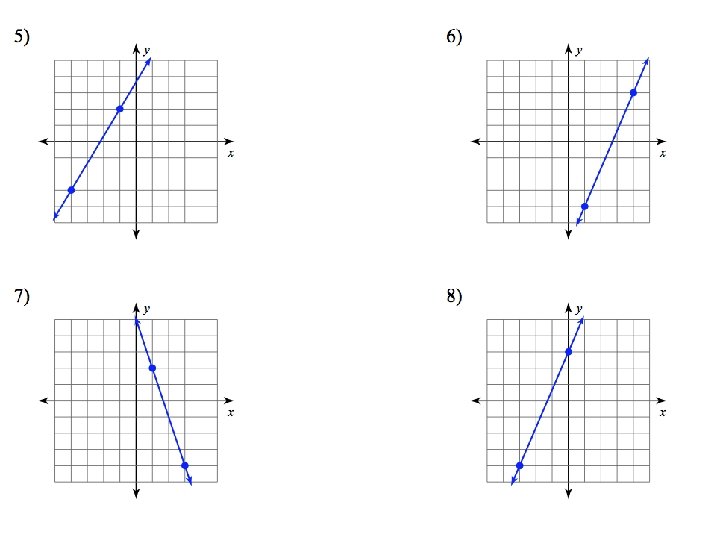
Do Now:


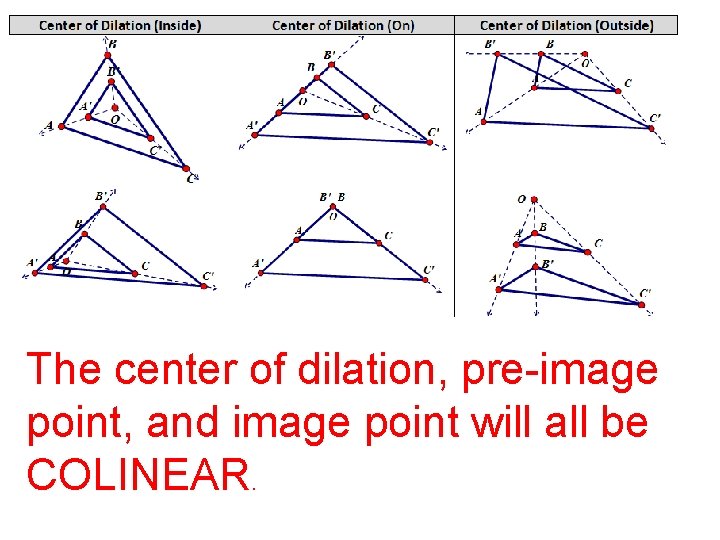
The center of dilation, pre-image point, and image point will all be COLINEAR.

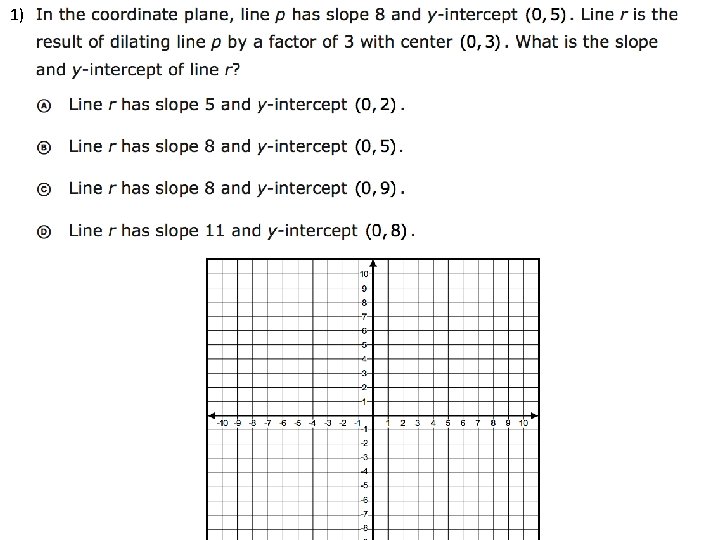
1)


