Dijet Transverse Thrust cross sections at D Veronica

Dijet Transverse Thrust cross sections at DØ Veronica Sorin University of Buenos Aires

Outline • Introduction: – Overview – The KT algorithm – Definition of the observable • Dijet Transverse Thrust cross section • Systematic uncertainties • Comparison with theory • Conclusions 2

Theoretical Introduction Quantum Chromodynamics: Fundamental Vertices describe the interaction between quarks and gluons, which carry color charge, conventionally called: blue, red and green. Main QCD characteristics: Asymptotic freedom: as the energy of the interaction increases, the strength of the coupling get smaller, allowing the aplication of perturbative techniques (p. QCD). Confinement: quarks and gluons cannot be seen as isolated particles, partons (q and g) are bound together into hadrons. Jet Physics 3

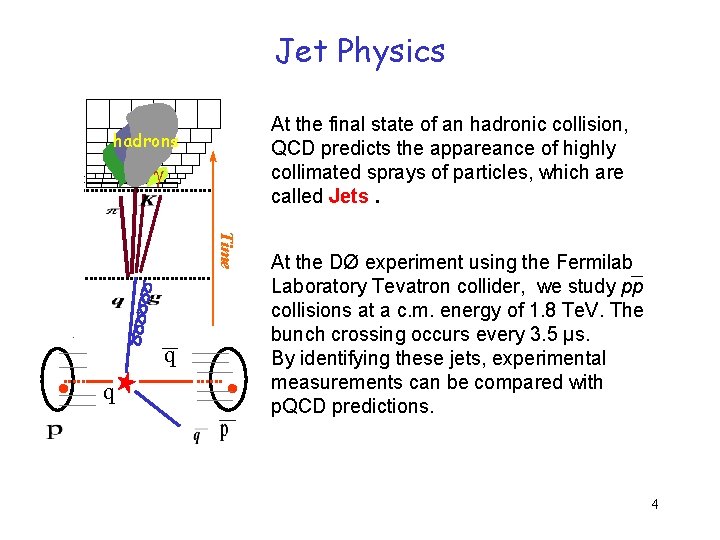
parton jetparticle jetcalorimeter jet Jet Physics CH FH At the final state of an hadronic collision, QCD predicts the appareance of highly collimated sprays of particles, which are called Jets. hadrons EM Time q · At the DØ experiment using the Fermilab Laboratory Tevatron collider, we study pp collisions at a c. m. energy of 1. 8 Te. V. The bunch crossing occurs every 3. 5 µs. By identifying these jets, experimental measurements can be compared with p. QCD predictions. 4

Panoramic view of the Fermilab Laboratory 5

Event Shapes Event shapes have been extensively studied at e+eand ep experiments to: • study spatial distribution of hadronic final states • test perturbative QCD predictions • extract a precise value of s • recently to test QCD developments like resummation calculations and non-perturbative corrections Resummations: needed at small values of the shape variable where fixed-order perturbative calculations are expected to fail. 6

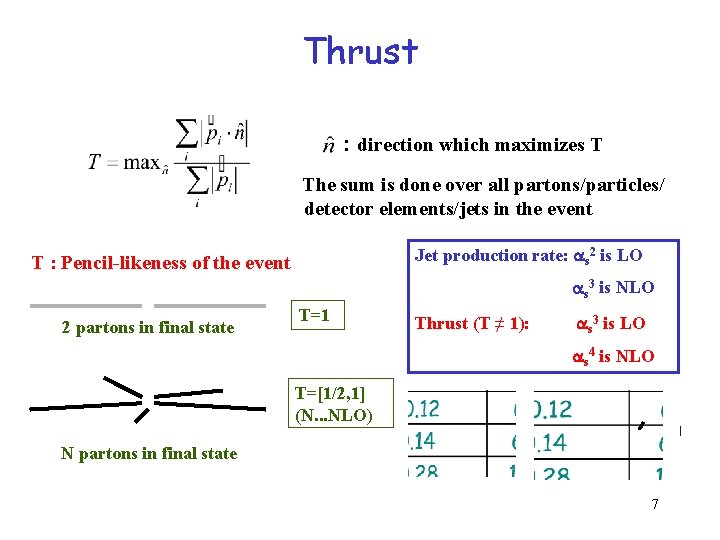
Thrust : direction which maximizes T The sum is done over all partons/particles/ detector elements/jets in the event Jet production rate: s 2 is LO T : Pencil-likeness of the event s 3 is NLO 2 partons in final state T=1 Thrust (T ≠ 1): s 3 is LO s 4 is NLO T=[1/2, 1] (N. . . NLO) N partons in final state 7

T in hadron colliders Busy environment: underlying event, pile-up, multiple interactions and noise We have derived a correction to eliminate particles jets on average the energy contributions from sources other than the hard interaction itself. – c. m system is not the parton-parton c. m. The pp Thrust is not invariant under z boosts Transverse Thrust Lorentz invariant quantity TT 3 D 2 D By replacing momenta with transverse momenta 8

The DØ Calorimeters y q Z x • Transverse segmentation (towers) Dh x D = 0. 1 x 0. 1 • Liquid argon active medium and uranium absorber • Hermetic with full coverage s. E / E = 15% /ÖE |h| < 4. 2 s. E / E = 45% /ÖE for pions l int > 7. 2 (total) for electrons 9

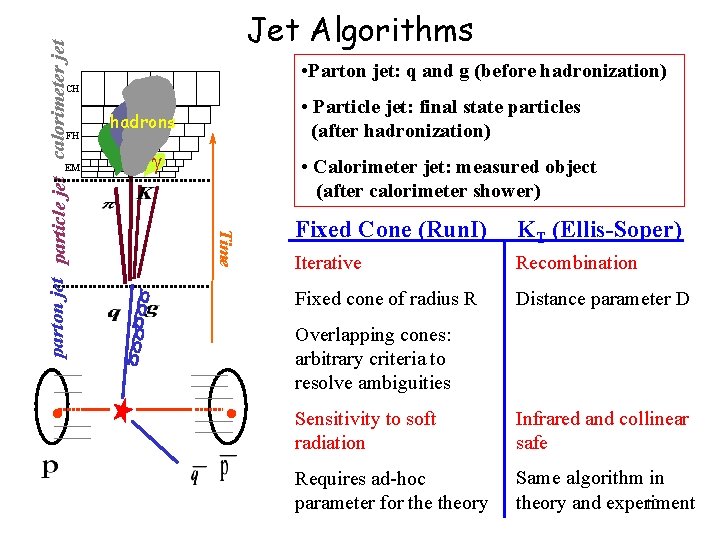
parton jet particle jet calorimeter jet Jet Algorithms • Parton jet: q and g (before hadronization) CH FH EM • Calorimeter jet: measured object (after calorimeter shower) Time · • Particle jet: final state particles (after hadronization) hadrons Fixed Cone (Run. I) KT (Ellis-Soper) Iterative Recombination Fixed cone of radius R Distance parameter D Overlapping cones: arbitrary criteria to resolve ambiguities · Sensitivity to soft radiation Infrared and collinear safe Requires ad-hoc parameter for theory Same algorithm in theory and experiment 10

Run. I DØ Analyses using the KT algorithm • “Subjet Multiplicity of Gluon and Quark Jets” Phys. Rev. D 65, 052008 (2002) • “The Inclusive Jet Cross Section” Phys. Lett. B 525, 211 (2002) • “Dijet Transverse Thrust Cross Sections” paper in preparation 11

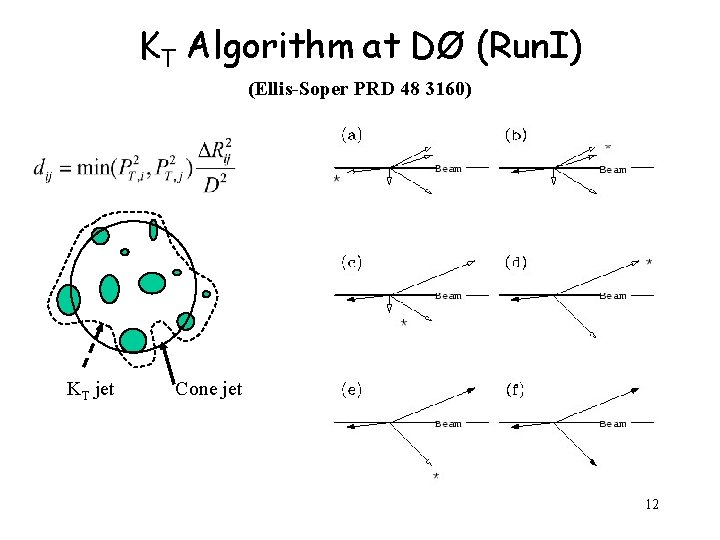
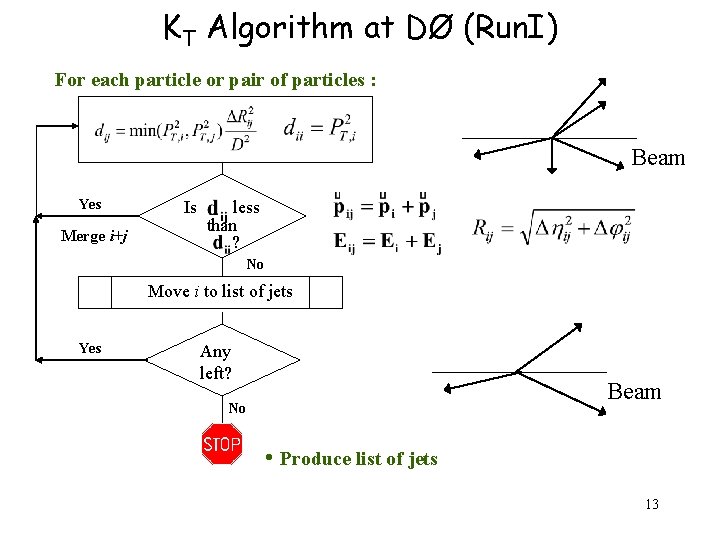
KT Algorithm at DØ (Run. I) (Ellis-Soper PRD 48 3160) KT jet Cone jet 12

KT Algorithm at DØ (Run. I) For each particle or pair of particles : Beam Yes Merge i+j Is less than ? No Move i to list of jets Yes Any left? Beam No • Produce list of jets 13

Jet Momentum Scale Correction Calorimeter jet Particle jet • Offset (O): Ur noise, pileup, multiple interactions, underlying event (ue) • Response (Rjet): Pmeas / Ptrue (using transverse momentum balance in g-jet events) 14

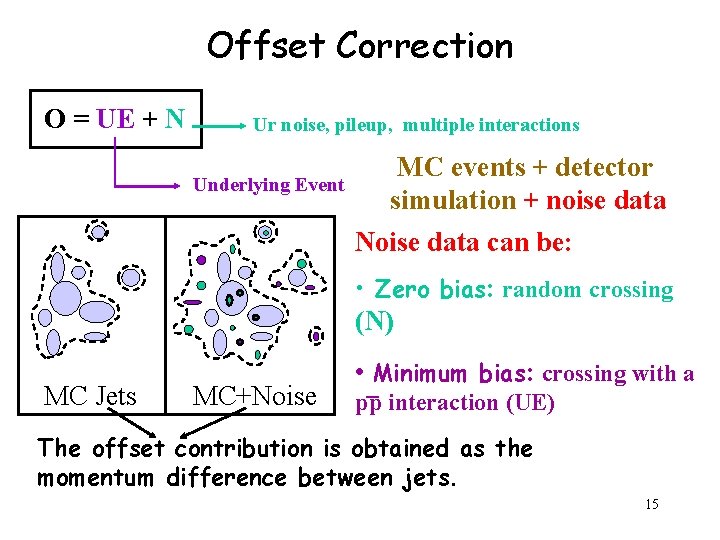
Offset Correction O = UE + N Ur noise, pileup, multiple interactions Underlying Event MC events + detector simulation + noise data Noise data can be: • Zero bias: random crossing (N) MC Jets MC+Noise • _Minimum bias: crossing with a pp interaction (UE) The offset contribution is obtained as the momentum difference between jets. 15

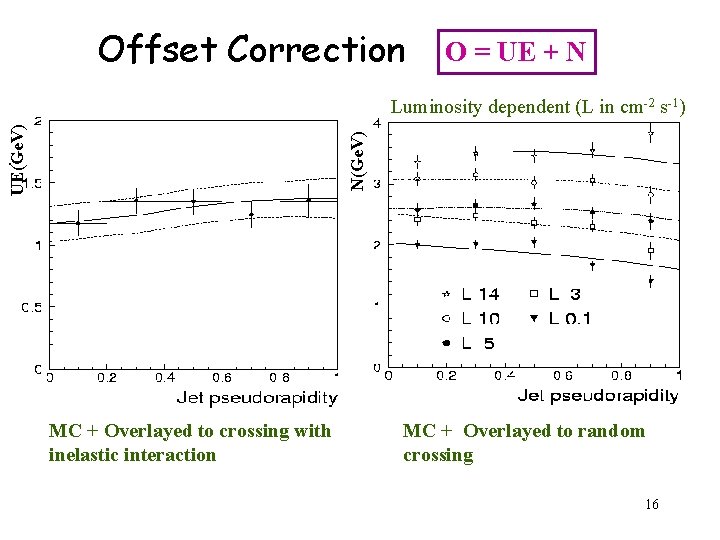
Offset Correction O = UE + N N(Ge. V) UE(Ge. V) Luminosity dependent (L in cm-2 s-1) . . . MC + Overlayed to crossing with inelastic interaction MC + Overlayed to random crossing 16

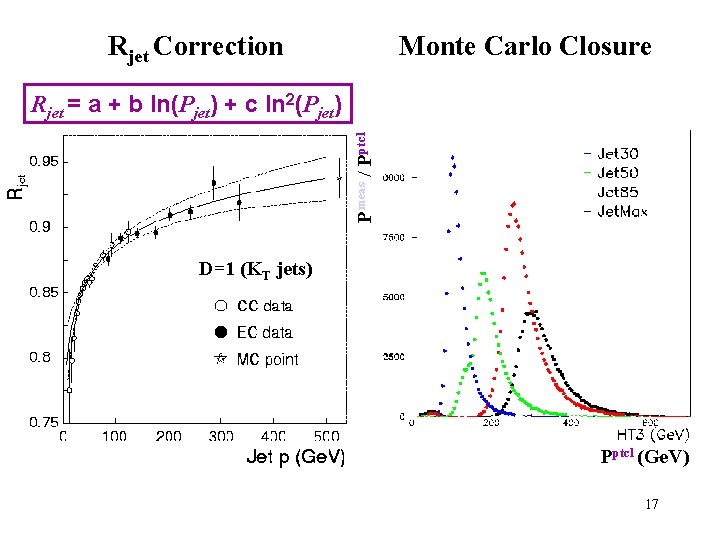
Monte Carlo Closure Rjet Correction Pmeas / Pptcl Rjet = a + b ln(Pjet) + c ln 2(Pjet) D=1 (KT jets) Pptcl (Ge. V) 17

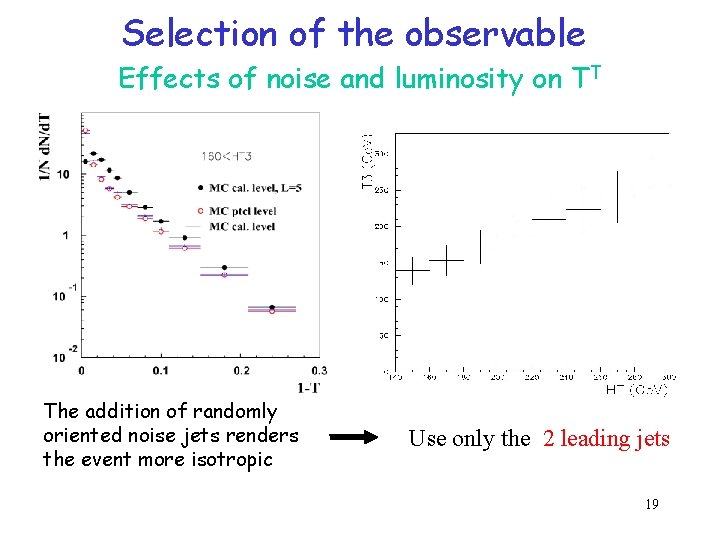
Dijet Transverse. Thrust • Sum done over jets • Jets have been reconstructed with the KT algorithm with D=1 Jet Momentum scale correction does not eliminate low energy jets ( high probability to originate 100% from background) distort the shape of the physical distributions Observable selected to reduce detector effects and maximize the signal in a hadron collider. Only the two leading jets will be used to calculate Thrust The spatial configuration of the two leading jets inherits the information of the other jets in the event 18

Selection of the observable Effects of noise and luminosity on TT The addition of randomly oriented noise jets renders the event more isotropic Use only the 2 leading jets 19

Selection of the observable The event energy scale Look for a variable correlated with Q 2 and with low sensitivity to noise HT 3 (scalar sum of the transverse momentum of the three leading jets) Noise jets ET 3 spectrum HT 3 vs HT Data HT at parton level: measure of Q 2 20

Brief Recapitulation • Measurement of cross section as a function of HT 3 • Using jets for which we have derived a correction that eliminates on average the contributions not related with the hard interaction. 120 o O( s 3) calculations can not cover the whole physical range: for , the LO calculation is O( s 4) • Test quality of QCD predictions • Study significance of resummation calculations 21

Coming up now…. • Observed Dijet Transverse Thrust Cross Sections • Systematic Uncertainties: – Momentum Scale Correction – Energy and Angular resolutions – Unfolding • Final results and Comparison with Theory • Conclusions 22

Dijet Transverse Thrust cross section KT algorithm (parameter D = 1) Event Selection: • Vertex cut (| z | < 50 cm, e ~ 90 %) • Cut on missing ET (ET/p. Tlj < 0. 7, e ~ 99. 8 %) Jet Selection: • Jet quality cuts (e ~ 99. 5 % ) ( 0. 05 < EMF < 0. 95, CHF < 0. 4 ) • Kinematic cuts: | 1, 2| < 1 23

HT 3 : scalar sum of the transverse momentum of the three leading jets. ( use 3 rd jet only when | 3 | < 3) It is presented in four HT 3 ranges Four single jet triggers are used for different HT 3 ranges where they are fully efficient. HT 3 distributions 24

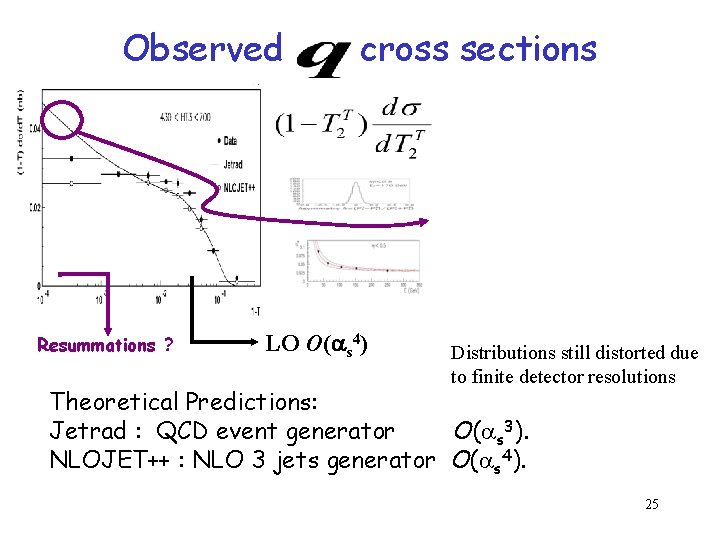
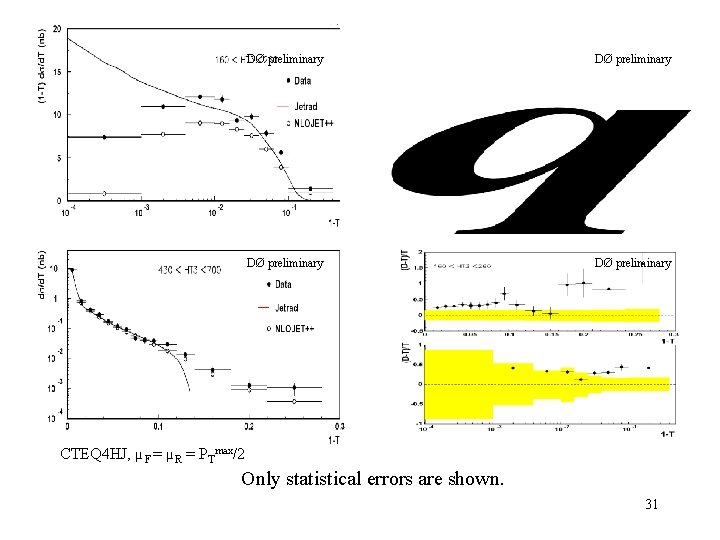
Observed Resummations ? cross sections LO O( s 4) Distributions still distorted due to finite detector resolutions Theoretical Predictions: Jetrad : QCD event generator O( s 3). NLOJET++ : NLO 3 jets generator O( s 4). 25

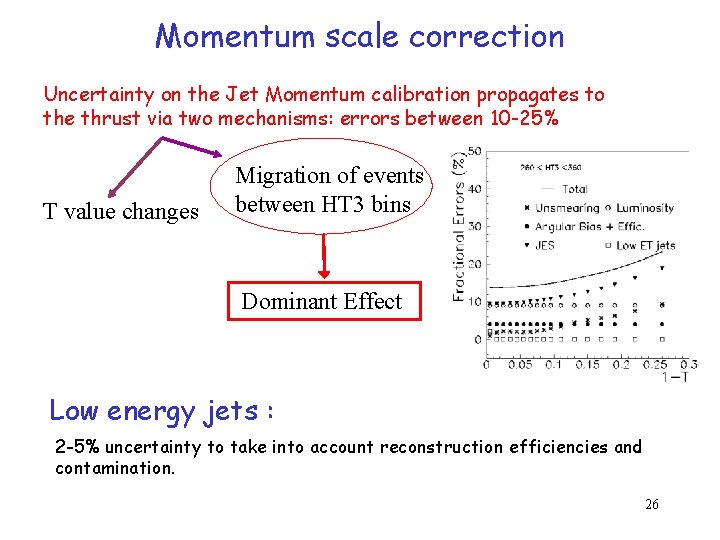
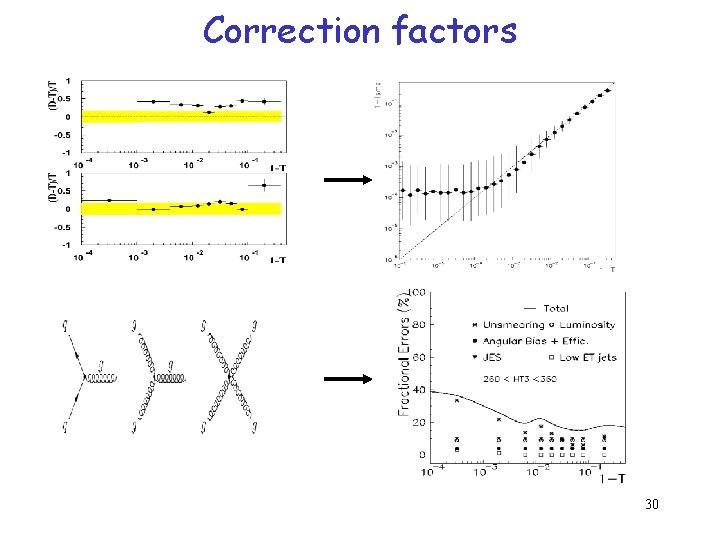
Momentum scale correction Uncertainty on the Jet Momentum calibration propagates to the thrust via two mechanisms: errors between 10 -25% T value changes Migration of events between HT 3 bins Dominant Effect Low energy jets : 2 -5% uncertainty to take into account reconstruction efficiencies and contamination. 26

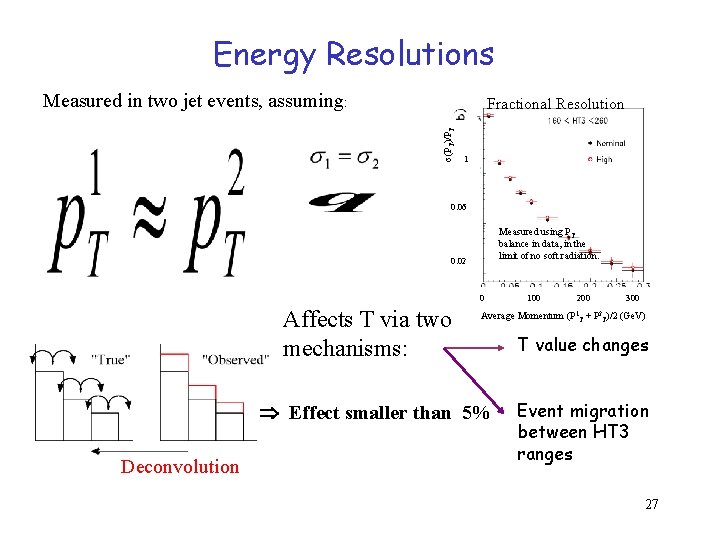
Energy Resolutions Measured in two jet events, assuming: σ(PT)/PT Fractional Resolution 1 0. 06 Measured using PT balance in data, in the limit of no soft radiation. 0. 02 0 Affects T via two mechanisms: 200 300 Average Momentum (P 1 T + P 2 T)/2 (Ge. V) Effect smaller than 5% Deconvolution 100 T value changes Event migration between HT 3 ranges 27

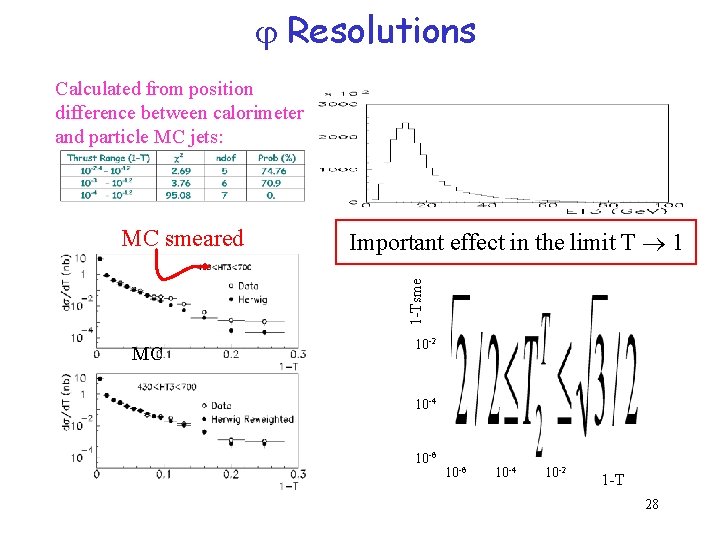
Resolutions Calculated from position difference between calorimeter and particle MC jets: Important effect in the limit T 1 1 -Tsme MC smeared MC 10 -2 10 -4 10 -6 10 -4 10 -2 1 -T 28

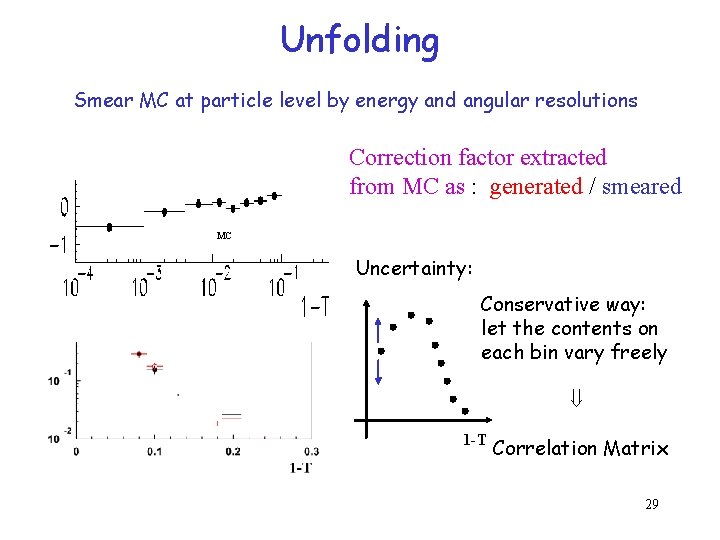
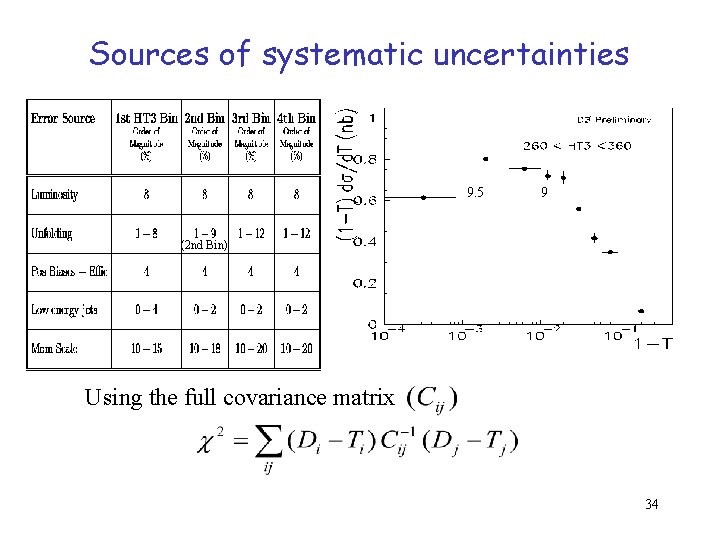
Unfolding Smear MC at particle level by energy and angular resolutions Correction factor extracted from MC as : generated / smeared MC Uncertainty: Conservative way: let the contents on each bin vary freely 1 -T Correlation Matrix 29

Correction factors 30

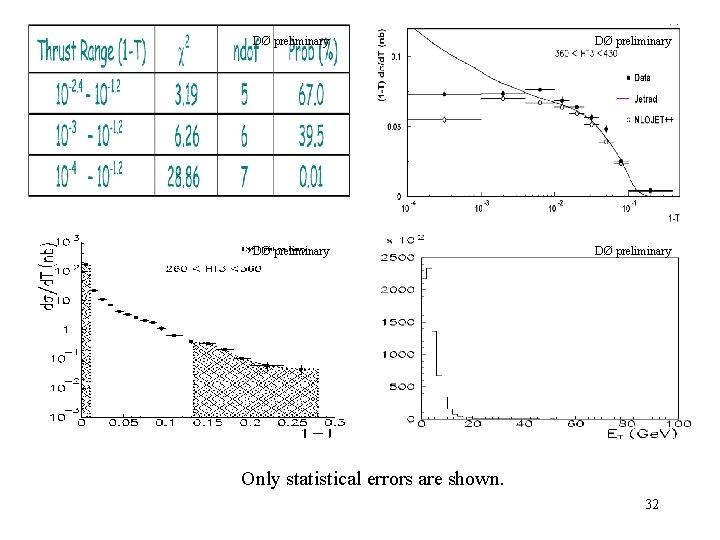
DØ preliminary CTEQ 4 HJ, µF = µR = PTmax/2 Only statistical errors are shown. 31

DØ preliminary Only statistical errors are shown. 32

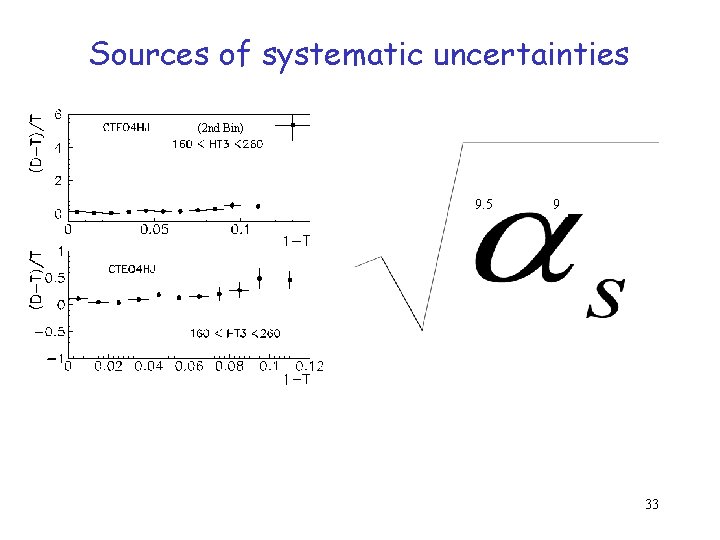
Sources of systematic uncertainties (2 nd Bin) 9. 5 9 33

Sources of systematic uncertainties 9. 5 9 (2 nd Bin) Using the full covariance matrix 34

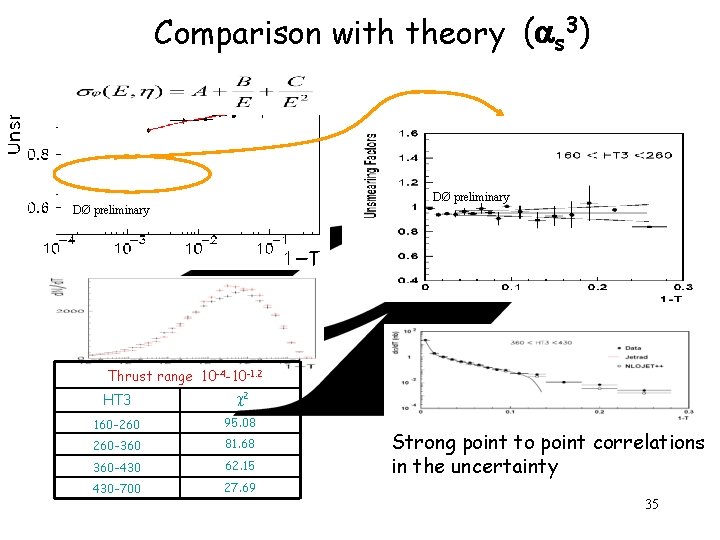
DØ preliminary Comparison with theory ( s 3) DØ preliminary Thrust range 10 -4 -10 -1. 2 HT 3 2 160 -260 95. 08 260 -360 81. 68 360 -430 62. 15 430 -700 27. 69 Strong point to point correlations in the uncertainty 35

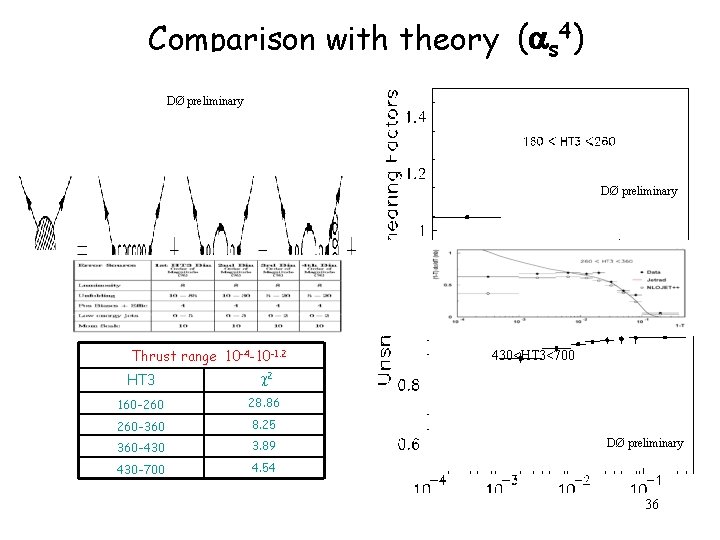
Comparison with theory ( s 4) DØ DØpreliminary DØ preliminary Thrust range 10 -4 -10 -1. 2 HT 3 2 160 -260 28. 86 260 -360 8. 25 360 -430 3. 89 430 -700 4. 54 430<HT 3<700 DØ preliminary 36

Conclusions The first precise measurement of an event shape distribution such as d /d. T in a hadron collider. The prediction s 3 (Jetrad) agrees with data except for high T values, 1 -T < 10 -3 and in the low region 1 -T > 0. 12. Resummation calculations needed in the limit T 1. Between the LO prediction is O( s 4). Excellent opportunity to test the recently developed NLO 3 -jet generators. This prediction (NLOJET++) agrees with data over the whole T range (T ≠ 1), except in the limit T 1 for low HT 3, where higher order corrections are still important. 37