Digraphs Reachability Connectivity Transitive Closure FloydWarshall Algorithm BOS

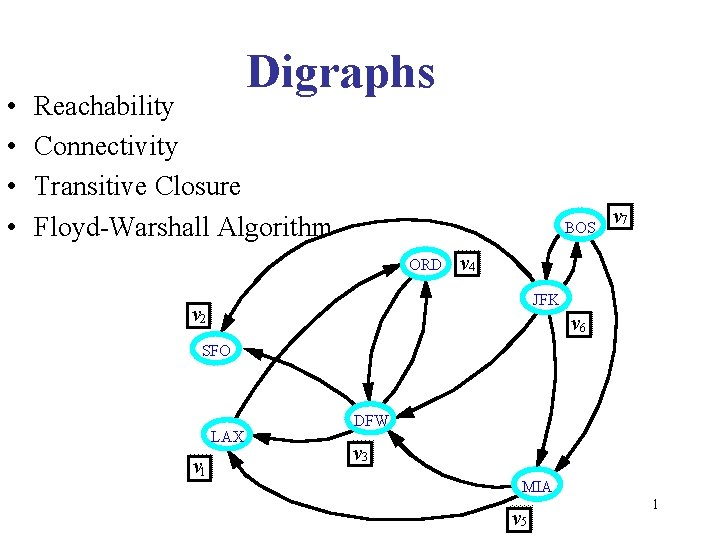
• • Digraphs Reachability Connectivity Transitive Closure Floyd-Warshall Algorithm BOS ORD v 7 v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 1

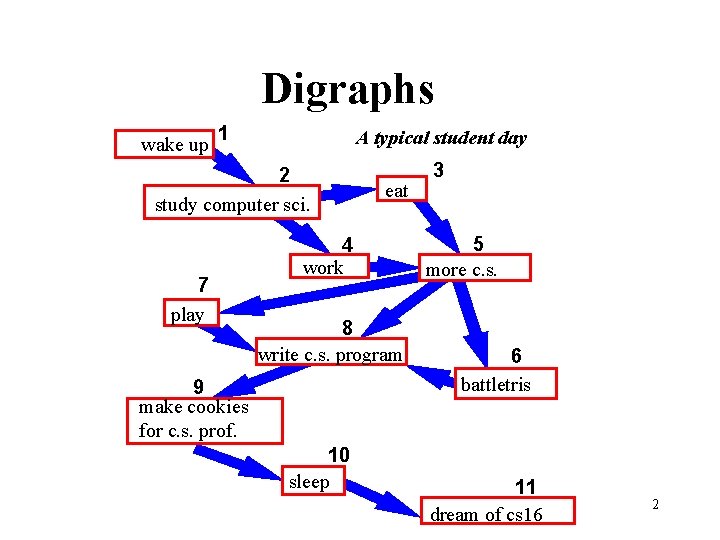
Digraphs wake up 1 A typical student day 2 study computer sci. 7 play eat 4 work 8 write c. s. program 9 make cookies for c. s. prof. 10 sleep 3 5 more c. s. 6 battletris 11 dream of cs 16 2

What’s a Digraph? • a) A small burrowing animal with long sharp teeth and a unquenchable lust for the blood of computer science majors • b) A distressed graph a • c) A directed graph Each edge goes in one direction Edge (a, b) goes from a to b, but not b to a You’re saying, “Yo, how about an example of how we might be enlightened by the use of digraphs!!” - Well, if you insist. . . 3

Applications Maps: digraphs handle one-way streets (especially helpful in Providence) 4

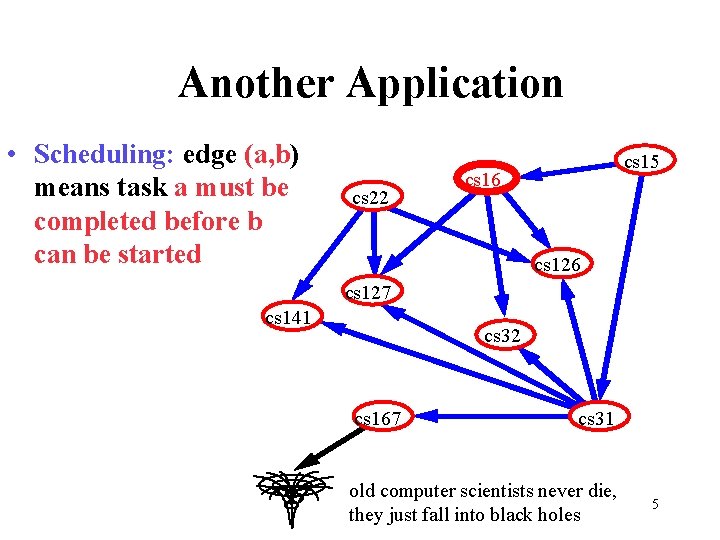
Another Application • Scheduling: edge (a, b) means task a must be completed before b can be started cs 22 cs 15 cs 16 cs 127 cs 141 cs 32 cs 167 cs 31 old computer scientists never die, they just fall into black holes 5

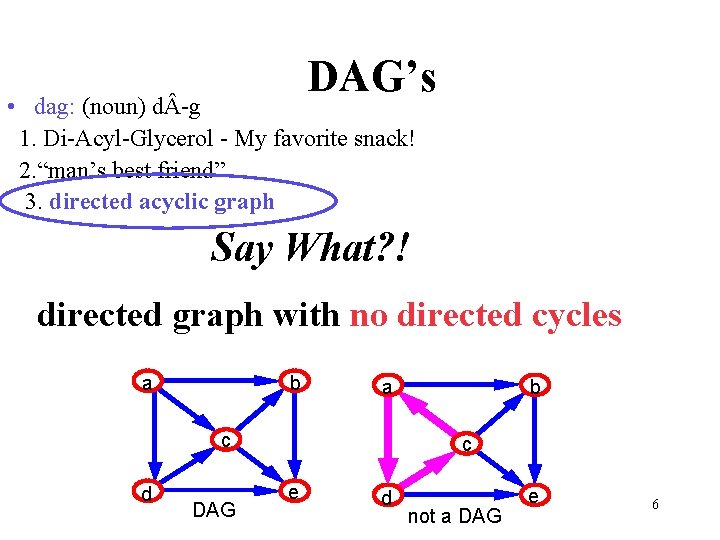
DAG’s • dag: (noun) d -g 1. Di-Acyl-Glycerol - My favorite snack! 2. “man’s best friend” 3. directed acyclic graph Say What? ! directed graph with no directed cycles a b a c d DAG b c e d not a DAG e 6

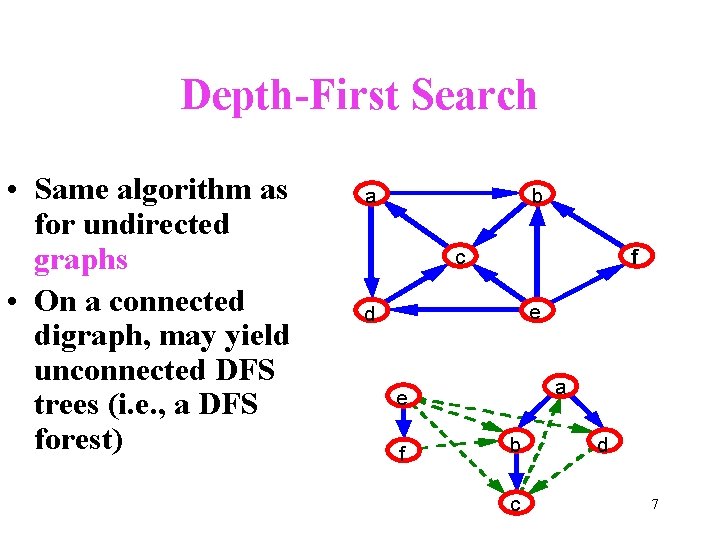
Depth-First Search • Same algorithm as for undirected graphs • On a connected digraph, may yield unconnected DFS trees (i. e. , a DFS forest) a b c f e d a e f b c d 7

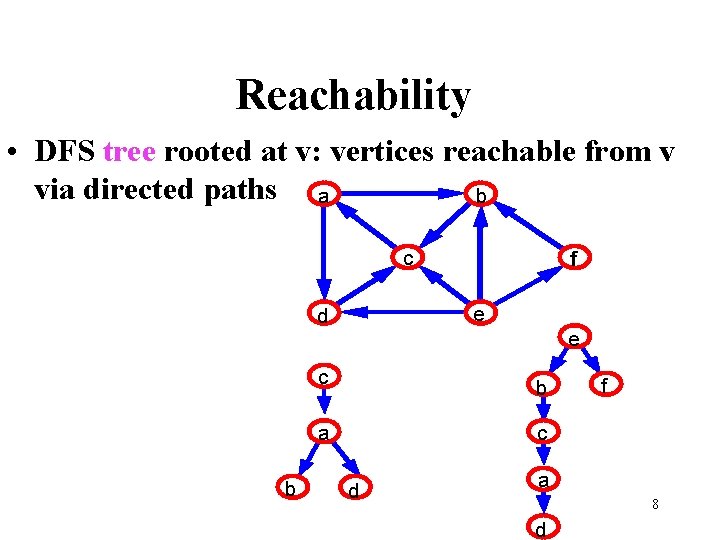
Reachability • DFS tree rooted at v: vertices reachable from v via directed paths a b c e d b f e c b a c d f a 8 d

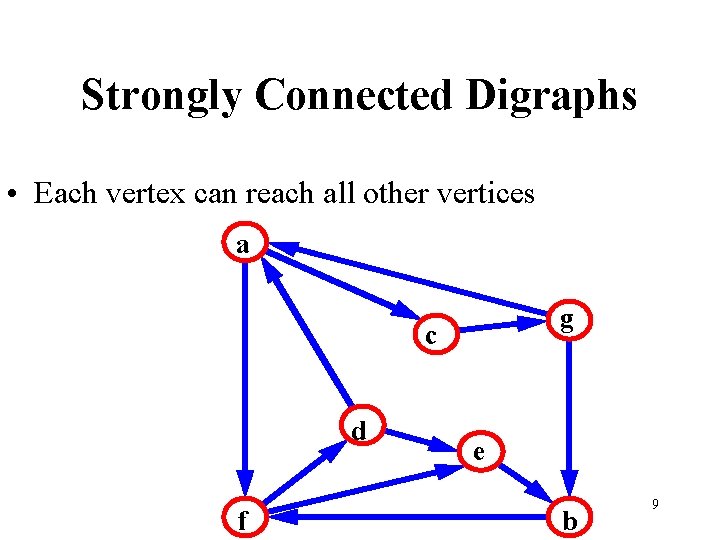
Strongly Connected Digraphs • Each vertex can reach all other vertices a g c d f e b 9

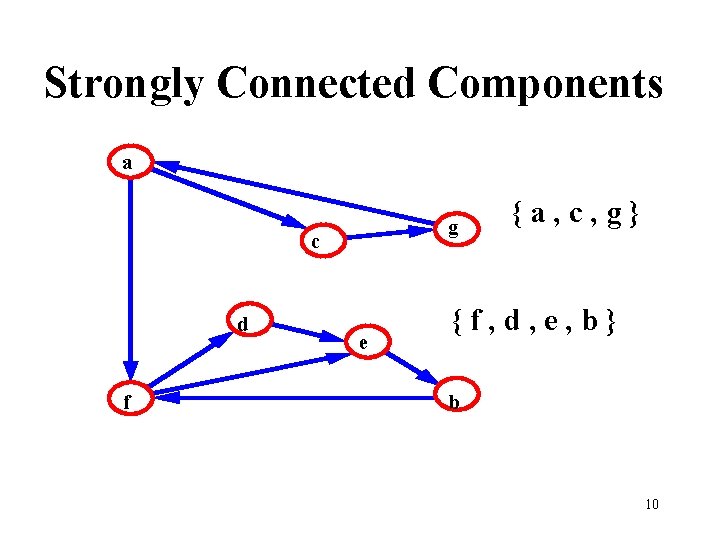
Strongly Connected Components a g c d f e {a, c, g} {f, d, e, b} b 10

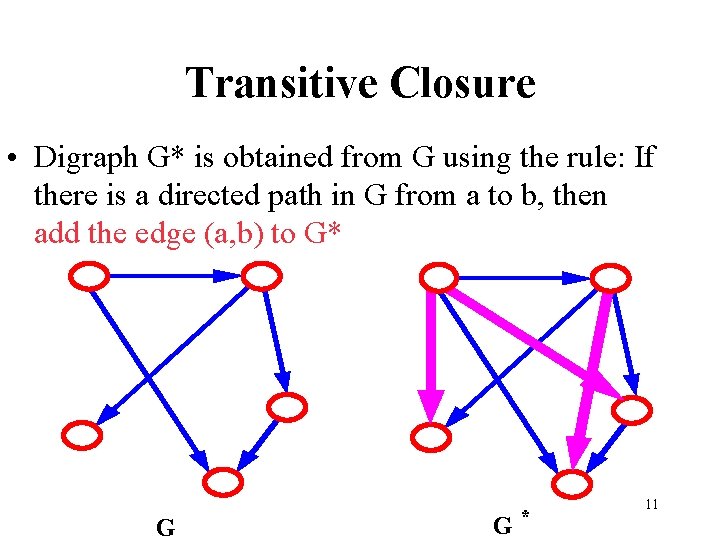
Transitive Closure • Digraph G* is obtained from G using the rule: If there is a directed path in G from a to b, then add the edge (a, b) to G* G G * 11

Computing the Transitive Closure • We can perform DFS starting at each vertex • Time: O(n(n+m)) • Alternatively. . . Floyd-Warshall Algorithm: if there's a way to get from A to B and from B to C then there's a way to get from A to C. 12 “Pink” Flo yd

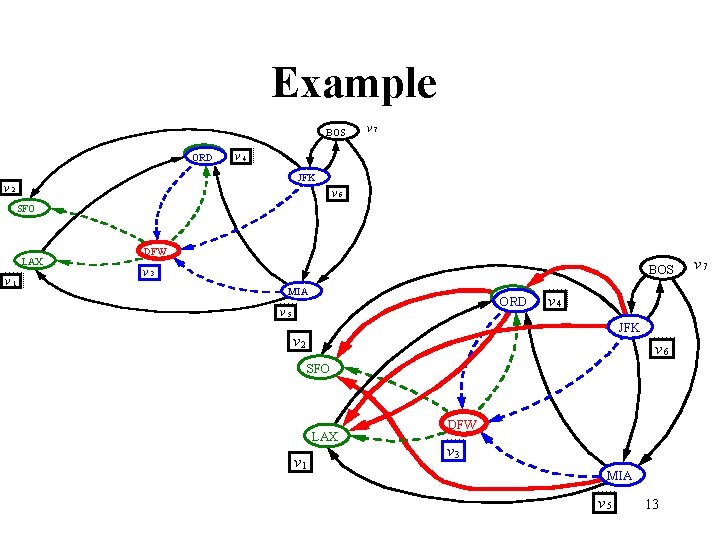
Example BOS ORD v 7 v 4 JFK v 2 v 6 SFO LAX v 1 DFW BOS v 3 MIA ORD v 5 v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 13 v 7

Floyd-Warshall Algorithm Assumes that methods are. Adjacent and insert. Directed. Edge take O(1) time (e. g. , adjacency matrix structure) Algorithm Floyd. Warshall(G) let v 1. . . vn be an arbitrary ordering of the vertices G 0 = G for k = 1 to n do // consider all possible routing vertices vk Gk= Gk-1// these are the only ones you need to store for each (i, j = 1, . . . , n) (i != j) (i, j != k) do // for each pair of vertices vi and vj if Gk-1. are. Adjacent(vi, vk) and Gk-1. are. Adjacent(vk, vj) then Gk. insert. Directed. Edge(vi, vj, null) return Gn Digraph Gk is the subdigraph of the transitive closure of G induced by paths with intermediate vertices in the set { v 1, . . . , vk } Running time: O(n 3) 14

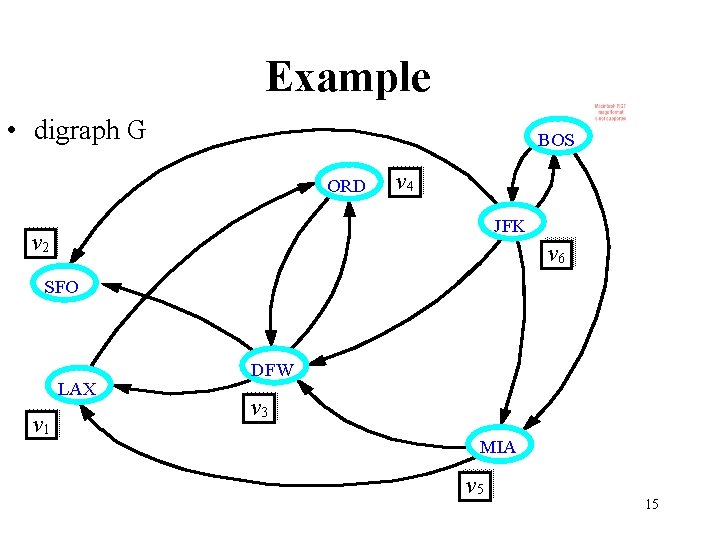
Example • digraph G BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 15

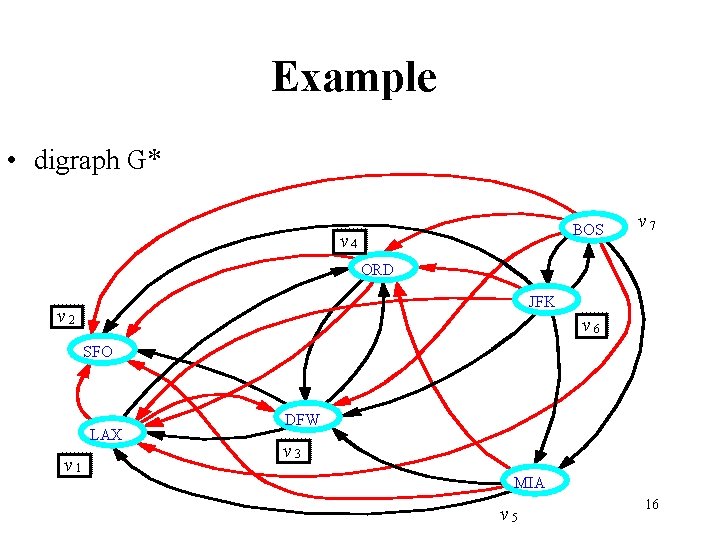
Example • digraph G* BOS v 4 v 7 ORD JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 16

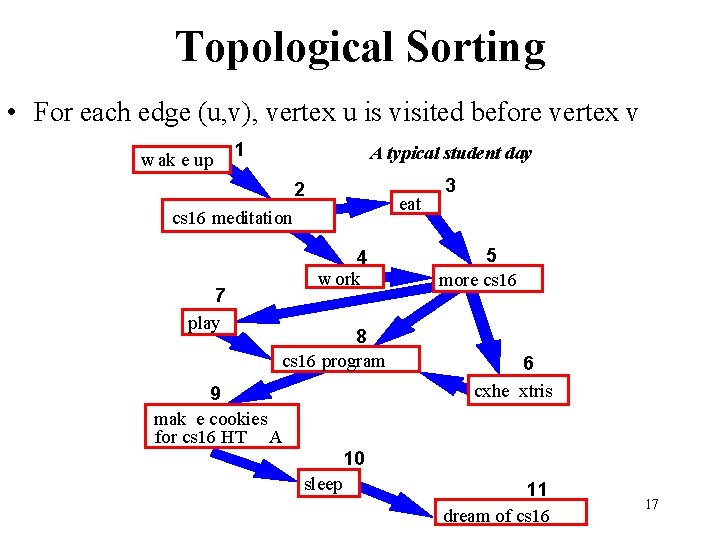
Topological Sorting • For each edge (u, v), vertex u is visited before vertex v w ak e up 1 A typical student day 2 eat cs 16 meditation 7 play 4 w ork 8 cs 16 program 9 mak e cookies for cs 16 HT A 3 5 more cs 16 6 cxhe xtris 10 sleep 11 dream of cs 16 17

Topological Sorting • Topological sorting may not be unique A ABCD or C B D ACBD - You make the call! 18

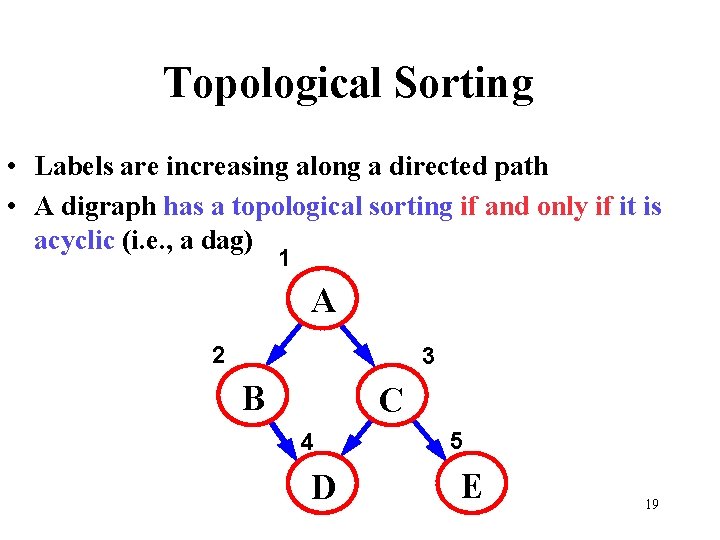
Topological Sorting • Labels are increasing along a directed path • A digraph has a topological sorting if and only if it is acyclic (i. e. , a dag) 1 A 2 3 B C 4 D 5 E 19

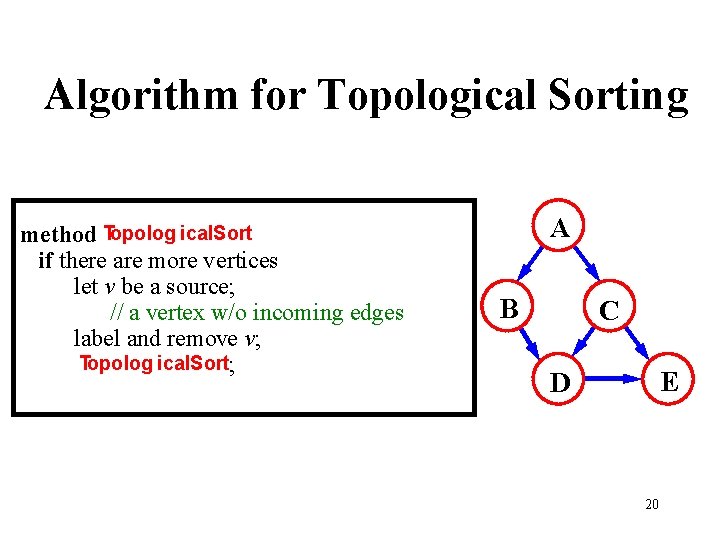
Algorithm for Topological Sorting method Topolog ical. Sort if there are more vertices let v be a source; // a vertex w/o incoming edges label and remove v; Topolog ical. Sort; A B C E D 20

Algorithm (continued) • Simulate deletion of sources using indegree counters Top. Sort(Vertex v); label v; foreach edge(v, w) indeg(w) = indeg(w) - 1; if indeg(w) = 0 Top. Sort(w); Compute indeg(v) for all vertices Foreach vertex v do if v not labeled and indeg(v) = 0 then Top. Sort(v) 21

Example ? ? ? 0 A 0 B 1 C D ? E ? 3 F ? 2 1 G H ? ? 2 1 I ? 22 3