Digitlis rendszerek I 20042005 tanv I flv Dr

Digitális rendszerek I. 2004/2005 tanév I. félév Dr. Ádám Tihamér Villamosmérnöki Intézet, Automatizálási Tanszék Informatikai épület, 207. Telefon: 565 140 (közvetlen), 19 -32 (egyetemi mellék) email: adam@mazsola. iit. uni-miskolc. hu hompage: http: //mazsola. iit. uni-miskolc. hu Digitálistechnika I. 1

A logikai feladat fogalma • Feladat: Présgép biztonságos üzemeltetése. • Szöveges megfogalmazás: • A gép csak akkor működjön, ha a kezelő egyik kezével lezárja a fedelet, másik kezével pedig megnyomja a működtető BE gombot. • A működési feltételek táblázatos összefoglalása Digitálistechnika I. 2

A logikai feladat fogalma Feltételek Következmény Védőrács állapot BE gomb állapot présgép Nyitott Ki Áll Nyitott be Áll Zárt Ki Áll Zárt Be Működik Logikai feladat: ahol véges számú feltételek közül egyesek teljesüléséhez egyértelműen hozzá kell rendelni valamilyen előírás szerint véges számú következmény közül egy-egy következményt. A logikai feladat megoldásához logikai döntések szükségesek. Digitálistechnika I. 3

A logikai feladat fogalma A jelek véges számú értékeket vehetnek fel. Mi a kétértékű jelek rendszerével foglalkozunk: A kétértékű rendszerek a legmegbízhatóbbak. A kétértékű jelekkel működő logikai hálózatokkal foglalkozunk. Kétértékű logikai rendszerek leírására a kettes számrendszer használható. A bemeneti pontok mindegyikéhez egy-egy n bites bináris szám egy-egy helyiértéke rendelhető. Így a bemeneti pontok minden lehetséges együtteséhez egy-egy n jegyű bináris szám rendelhető, ahol a 0 és 1 érték jelzi, hogy a jel értéke a két lehetséges érték közül melyik. Így a bemeneti értékeknek 2 n féle együttese fordulhat elő. Ez egy 2 elemből álló ismétlődéses kombináció, ezért bemeneti kombinációnak nevezzük. M kimenet esetén így 2 m féle kimeneti kombináció lehet. Digitálistechnika I. 4

A logikai feladat fogalma A fenti feladat leírása a fentiek szerint: Feltételek Következm ény Védőrács állapot BE gomb állapot présgép Nyitott Ki Áll Nyitott be Áll Zárt Ki Áll Zárt Be Működik Digitálistechnika I. 5

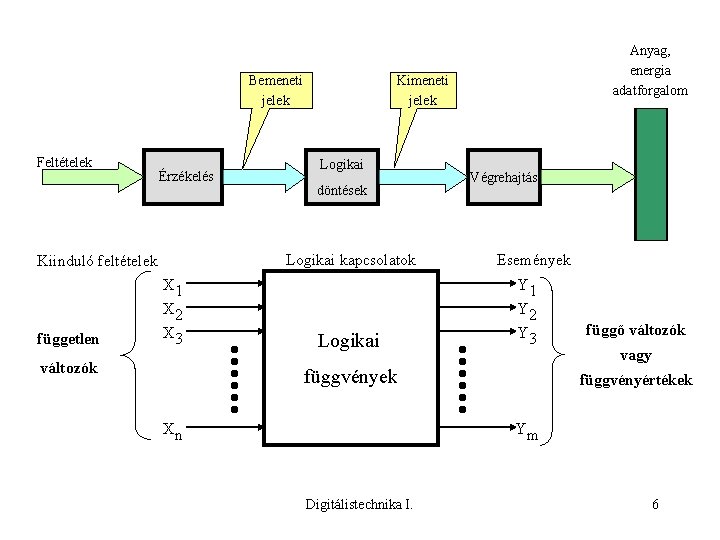
Bemeneti jelek Feltételek Érzékelés független Kimeneti jelek Logikai döntések Logikai kapcsolatok Kiinduló feltételek Anyag, energia adatforgalom Végrehajtás Események X 1 Y 1 X 2 X 3 Y 2 Y 3 változók Logikai függvények Xn függő változók vagy függvényértékek Ym Digitálistechnika I. 6

LOGIKAI VÁLLTOZÓK ÉS MŰVELETEK • LOGIKAI VÁLTOZÓK ÉS SZEMLÉLTETÉSÜK • LOGIKAI MŰVELETEK TULAJDONSÁGAI • BOOLE ALGEBRA AZONOSSÁGAI Digitálistechnika I. 7

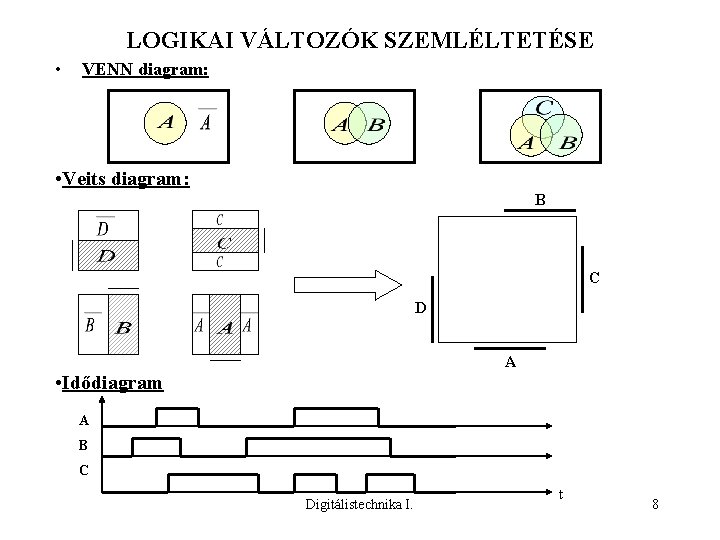
LOGIKAI VÁLTOZÓK SZEMLÉLTETÉSE • VENN diagram: • Veits diagram: B C D A • Idődiagram A B C Digitálistechnika I. t 8

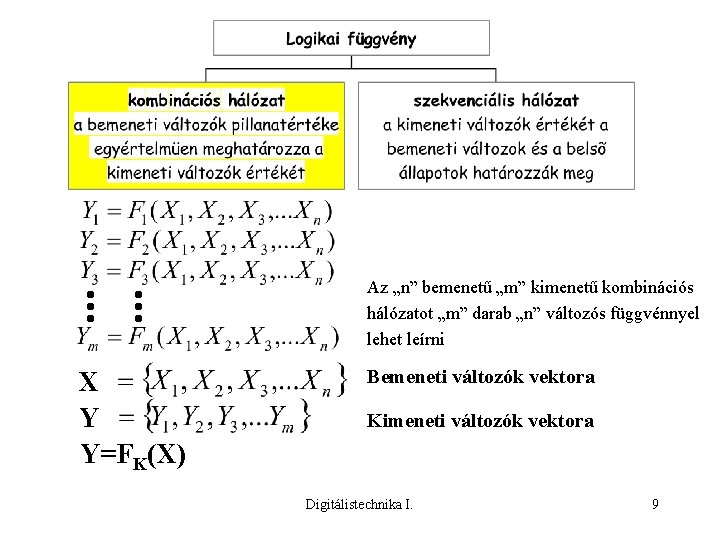
Az „n” bemenetű „m” kimenetű kombinációs hálózatot „m” darab „n” változós függvénnyel lehet leírni X Y Y=FK(X) Bemeneti változók vektora Kimeneti változók vektora Digitálistechnika I. 9

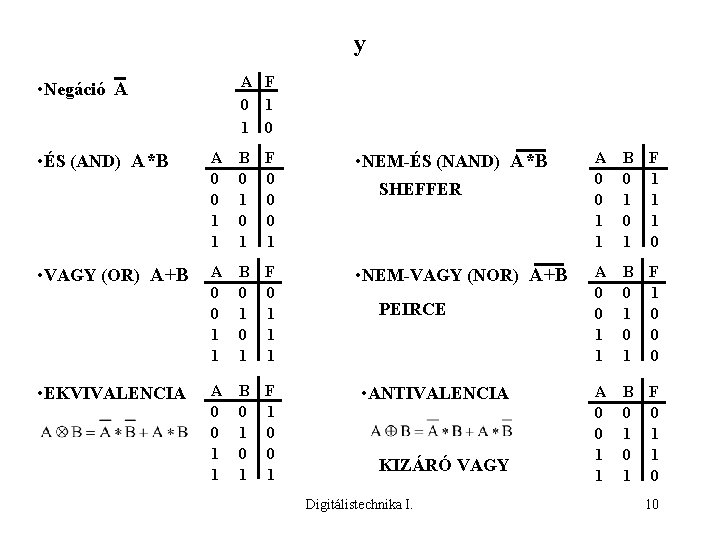
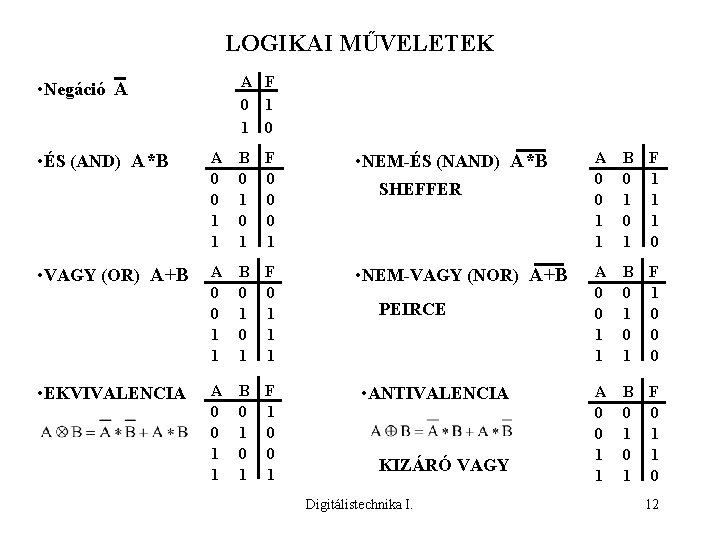
y A F 0 1 1 0 • Negáció A • ÉS (AND) A*B • VAGY (OR) A+B • EKVIVALENCIA A 0 0 1 1 B 0 1 F 0 0 0 1 • NEM-ÉS (NAND) A*B A 0 0 1 1 B 0 1 F 0 1 1 1 • NEM-VAGY (NOR) A+B A 0 0 1 1 B 0 1 F 1 0 0 1 SHEFFER PEIRCE • ANTIVALENCIA KIZÁRÓ VAGY Digitálistechnika I. A 0 0 1 1 B 0 1 F 1 1 1 0 A 0 0 1 1 B 0 1 F 1 0 0 0 A 0 0 1 1 B 0 1 F 0 1 1 0 10

A logikai (BOOLE) algebrai alapjai • Logikai (BOOLE-) algebra • BOOLE (1815 -1864) angol matematikus volt az első, aki a logikai, ill. a róla elnevezett BOOLE-algebra alapfogalmait bevezette és összefüggéseit vizsgálta a „The Mathematical of Logic” (1848) c. munkájában. Tulajdonképpen olyan szimbolikus jelölésmódot dolgozott ki, amely alkalmas volt a formális logikai problémáinak algebrai formában történő leírására. A megkezdett munkát kiváló matematikusok egész sora – mint SCHROEDER, RUSSEL, WHITEHEAD stb. – fejlesztette tovább. BOOLE – algebrának jelfogós kapcsolóáramkörök analízisére való felhasználása (1938 ban) SHANNON nevéhez fűződik. Digitálistechnika I. 11

LOGIKAI MŰVELETEK A F 0 1 1 0 • Negáció A • ÉS (AND) A*B • VAGY (OR) A+B • EKVIVALENCIA A 0 0 1 1 B 0 1 F 0 0 0 1 • NEM-ÉS (NAND) A*B A 0 0 1 1 B 0 1 F 0 1 1 1 • NEM-VAGY (NOR) A+B A 0 0 1 1 B 0 1 F 1 0 0 1 SHEFFER PEIRCE • ANTIVALENCIA KIZÁRÓ VAGY Digitálistechnika I. A 0 0 1 1 B 0 1 F 1 1 1 0 A 0 0 1 1 B 0 1 F 1 0 0 0 A 0 0 1 1 B 0 1 F 0 1 1 0 12

A LOGIKAI (BOOLE) MŰVELETEK TULAJDONSÁGAI I. III. IV. V. VI. Kommutativitás: A*B=B*A A+B=B+A Asszociativitás: (A*B)*C=A*(B*C)=A*B*C (A+B)+C=A+(B+C)=A+B+C Disztributivitás A*(B+C)=A*B+A*C A+(B*C)=(A+B)*(A+C) EGYSÉG- és NULLA-elem létezése: A*1=A A+0=A KOMPLEMENS-elem létezése: A*Ă=0 A+Ă=1 Abszorpciós tulajdonság: A(B+A) =A A+B*A=A Digitálistechnika I. 13

A BOOLE ALGEBRA AZONOSSÁGAI Digitálistechnika I. 14

3. ELŐADÁS LOGIKAI KAPCSOLATOK LEÍRÁSA • LOGIKAI FÜGGVÉNYKAPCSOLATOK MEGADÁSI MÓDJAI – – szöveges igazságtáblázatos algebrai grafikus • LOGIKAI FÜGGVÉNYEK SZABÁLYOS ALAKJAI • A DISZJUNKTÍV ÉS A KONJUNKTÍV ALAK KAPCSOLATA Digitálistechnika I. 15

LOGIKAI KAPCSOLATOK MEGADÁSI MÓDJAI • Szöveges leírás: Pl. : Négy résztvevős szavazógép a többségi elv alapján működik. Szavazat egyenlőség esetén az elnök szavazata dönt. • Táblázatos megadás: D 0 0 0 0 1 1 1 1 C 0 0 0 0 1 1 1 1 B 0 0 1 1 A 0 1 0 1 F 0 0 0 0 1 1 1 1 Ahol A, B, C, a tagok, D az elnök szavazata Digitálistechnika I. 16

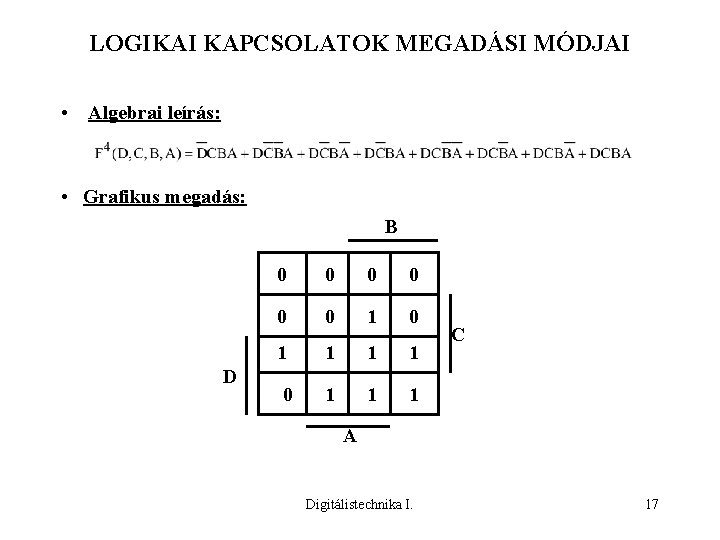
LOGIKAI KAPCSOLATOK MEGADÁSI MÓDJAI • Algebrai leírás: • Grafikus megadás: B D 0 0 0 1 0 1 1 1 C A Digitálistechnika I. 17

LOGIKAI FÜGGVÉNYEK SZABÁLYOS ALAKJAI minterm: A változók olyan ÉS kapcsolata, amelyben minden változó - ponált vagy negált - alakban egyszer és csakis egyszerepel Ahol n a független változók száma, i a term sorszáma maxterm: A változók olyan VAGY kapcsolata, amelyban minden változó - ponált vagy negált - alakban egyszer és csakis egyszerepel Ahol n a független változók száma, i a term sorszáma illetve Digitálistechnika I. 18

diszjunktív szabályos (kanonikus) alak: A mintermek VAGY kapcsolata Indexes alakban konjunktív szabályos (kanonikus) alak: A maxtermek ÉS kapcsolata Sorszámos alakban Digitálistechnika I. 19

A DISZJUNKTÍV ÉS A KONJUNKTÍV ALAK KAPCSOLATA A függvény igazságtáblázatával adott. A mintermes alak felírásakor a függvény logikai 1 értékeiből indulunk ki: az ezekhez tartozó bemenő változók logikai szorzatait (mintermeket) írjuk fel és képezzük a logikai szorzatok összegét. Ezt diszjunktív alaknak nevezzük. D 0 0 0 0 1 1 1 1 C 0 0 0 0 1 1 1 1 B 0 0 1 1 A 0 1 0 1 F 1 1 0 0 0 1 0 0 0 Digitálistechnika I. 20

A DISZJUNKTÍV ÉS A KONJUNKTÍV ALAK KAPCSOLATA • Egy másik lehetőség: a függvény 0 helyeiből indulunk ki, de ekkor a függvény negáltját kapjuk: • A függvényt újabb negálás után kapjuk: Digitálistechnika I. 21

A DISZJUNKTÍV ÉS A KONJUNKTÍV ALAK KAPCSOLATA • A De Morgan tétel segítségével ezt átalakítjuk: • Ezután felhasználásával kapjuk a • végeredményt: Digitálistechnika I. 22

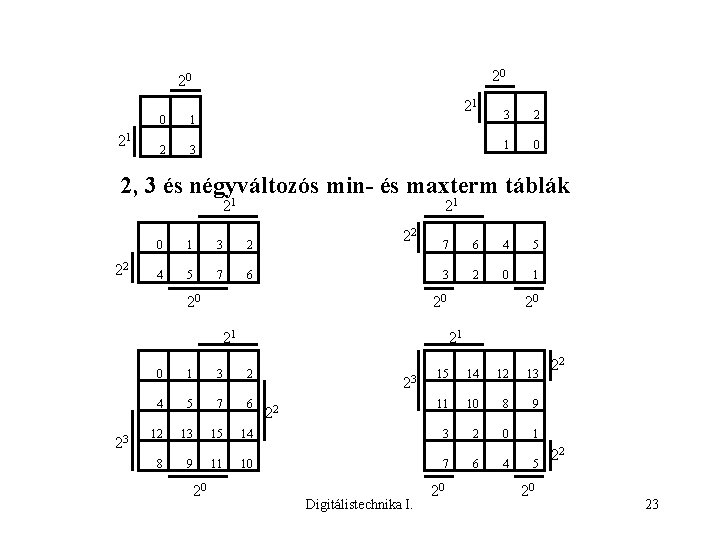
20 20 21 0 1 2 3 21 3 2 1 0 2, 3 és négyváltozós min- és maxterm táblák 21 22 21 0 1 3 2 4 5 7 6 22 20 7 6 4 5 3 2 0 1 20 21 23 21 0 1 3 2 4 5 7 6 12 13 15 8 9 11 20 20 15 14 12 13 11 10 8 9 14 3 2 0 1 10 7 6 4 5 23 22 Digitálistechnika I. 20 20 22 22 23

LOGIKAI FÜGGVÉNYEK EGYSZERŰSÍTÉSE • TERM ÖSSZEVONÁSI LEHETŐSÉGEK • A GRAFIKUS MINIMALIZÁLÁS LÉPÉSEI Digitálistechnika I. 24

LOGIKAI FÜGGVÉNYEK EGYSZERŰSÍTÉSE • A BOOLE algebra azonosságainak felhasználásával: 1 1 Az összevonás feltétele, hogy a két term csak egyetlen változóban különbözhet egymástól. A kérdéses változó az egyik termben ponált, a másik termben negált állapotban kell hogy szerepeljen • Szisztematikus eljárással: • Grafikus minimalizálás (Veitch-Karnaugh táblával) • Numerikus minimalizálás (Quine-Mc Cluskey-féle eljárás) Digitálistechnika I. 25

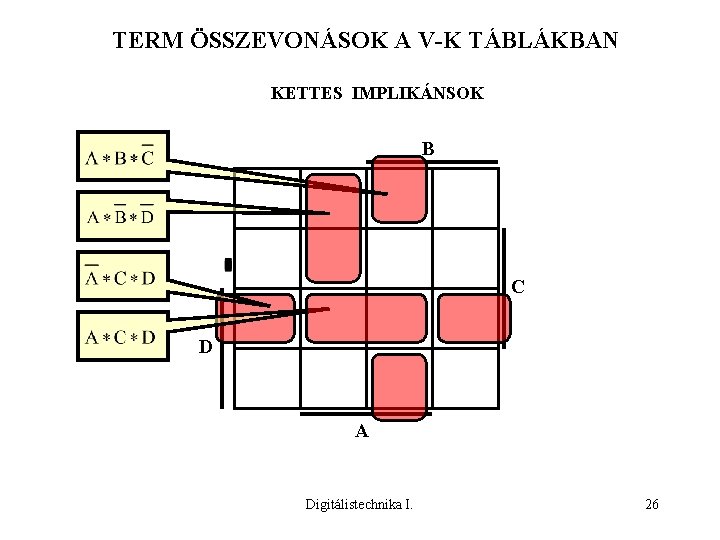
TERM ÖSSZEVONÁSOK A V-K TÁBLÁKBAN KETTES IMPLIKÁNSOK B C D A Digitálistechnika I. 26

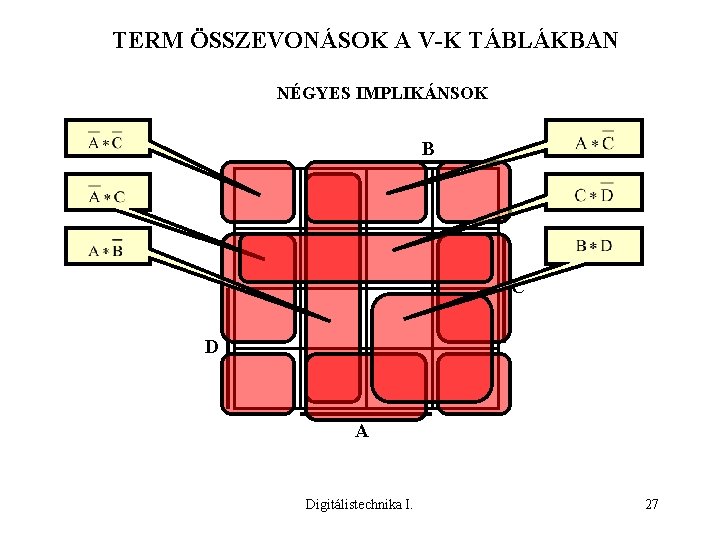
TERM ÖSSZEVONÁSOK A V-K TÁBLÁKBAN NÉGYES IMPLIKÁNSOK B C D A Digitálistechnika I. 27

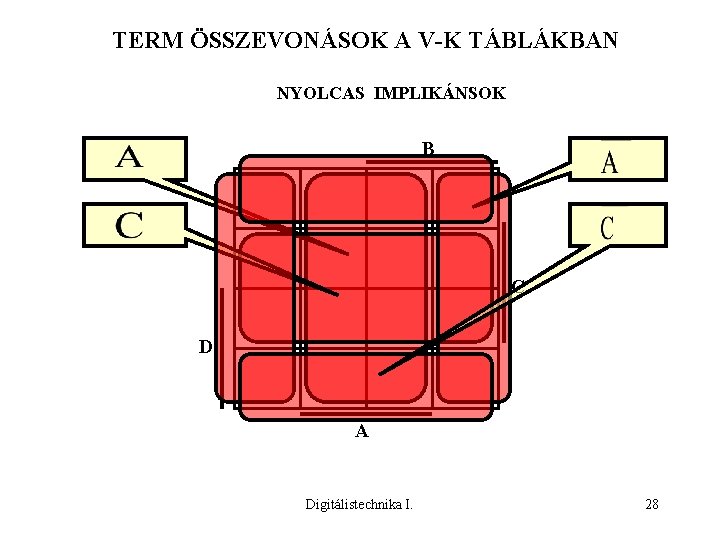
TERM ÖSSZEVONÁSOK A V-K TÁBLÁKBAN NYOLCAS IMPLIKÁNSOK B C D A Digitálistechnika I. 28

GRAFIKUS MINIMALIZÁLÁS A logikai függvények minimalizálási eljárása a primimplikánsok megkereséséből, majd pedig a szükséges primimplikánsok kiválasztásából áll. Primimplikánsok keresése: 1 Ábrázoljuk a függvényt VK táblán 2 A 2 i számú szimmetrikusan elhelyezkedő szomszédos 1 -gyel jelölt cellát egy tömbbé vonunk össze 3 Mindig a lehető legnagyobb tömböt célszerű kialakítani 4 Valamennyi 1 -gyel jelölt cellának legalább egy tömbben szerepelnie kell 5 Ugyanazon cella több tömbnek is eleme lehet 6 A táblák négy változóig széleiken egybefüggőnek tekinthetők Digitálistechnika I. 29

Valamely primimplikáns lényeges, ha tartalmaz olyan mni mintermet, amelyet minden más primiplikáns már nem tartalmaz. Azon tömbök lesznek a minimalizált függvény szükséges primimplikánsai, amelyek a függvény valamennyi 1 -gyel jelölt cellájának egyszeri lefedéséhez elengedhetetlenül szükségesek. A szükséges primimplikánsok kiválasztásának lépései: 1 Jelöljük meg egy-egy ponttal azon mintermeket, amelyeken csak egy hurok megy keresztül. Ezen tömbök lesznek a nélkülözhetetlen implikánsok. 2 Vonalkázzuk be a nélkülözhetetlen primimplikánsok által lefedett mintermeket 3 Maradt-e olyan 1 -egyel jelölt minterm, amelyet a nélkülözhetetlen primimplikánsok nem fedtek le? 4 A fennmaradó 1 -ek lefedésére válasszuk a legkevesebb és legnagyobb tömböt. Digitálistechnika I. 30

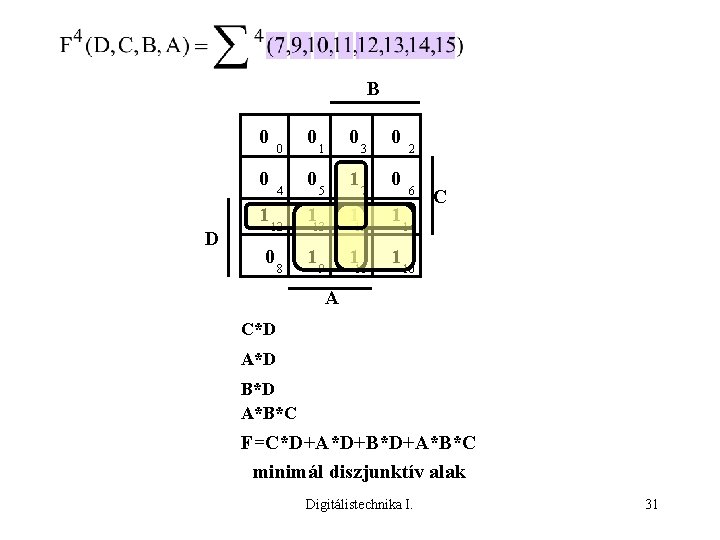
B 0 0 0 1 D 4 12 0 8 0 0 0 1 1 5 1 13 1 3 7 0 1 1 15 9 0 11 2 6 C 14 10 A C*D A*D B*D A*B*C F=C*D+A*D+B*D+A*B*C minimál diszjunktív alak Digitálistechnika I. 31

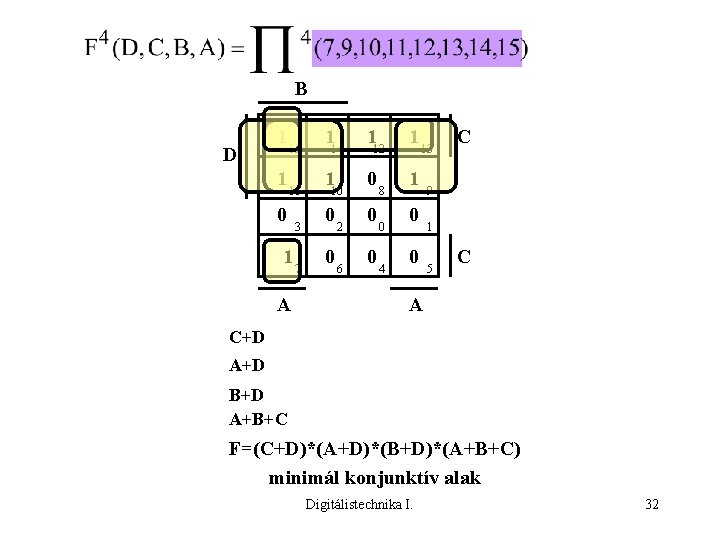
B D 1 1 15 11 0 1 A 3 7 1 1 1 0 14 10 0 0 2 6 12 0 0 8 0 4 1 13 1 0 0 C 9 1 5 C A C+D A+D B+D A+B+C F=(C+D)*(A+D)*(B+D)*(A+B+C) minimál konjunktív alak Digitálistechnika I. 32

5. ELŐADÁS RÉSZBEN MEGHATÁROZOTT FÜGGVÉNYEK • RÉSBEN MEGHATÁROZOTT LOGIKAI FÜGGVÉNYEK EGYSZERŰSÍTÉSE • EGYSZERÜSÍTÉS EKVIVALENCIA ÉS ANTIVALENCIA FÜGGVÉNYEKKEL • KÖZÖS RÉSZHÁLÓZAT KIALAKÍTÁSA Digitálistechnika I. 33

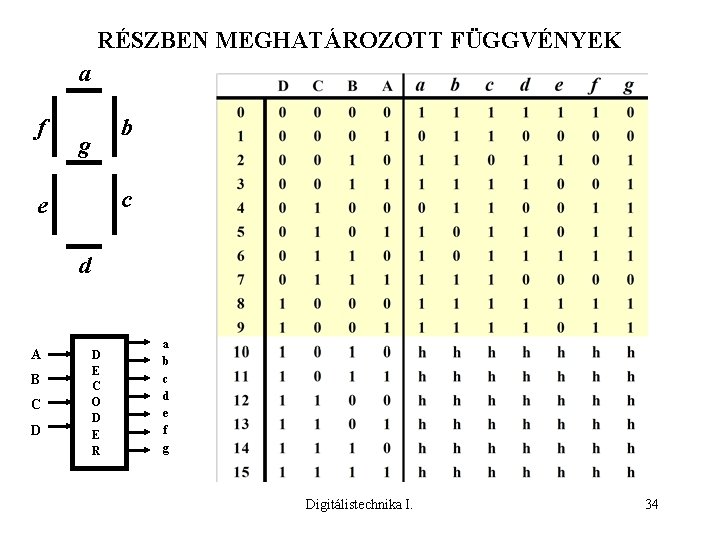
RÉSZBEN MEGHATÁROZOTT FÜGGVÉNYEK a f g b c e d A B C D D E C O D E R a b c d e f g Digitálistechnika I. 34

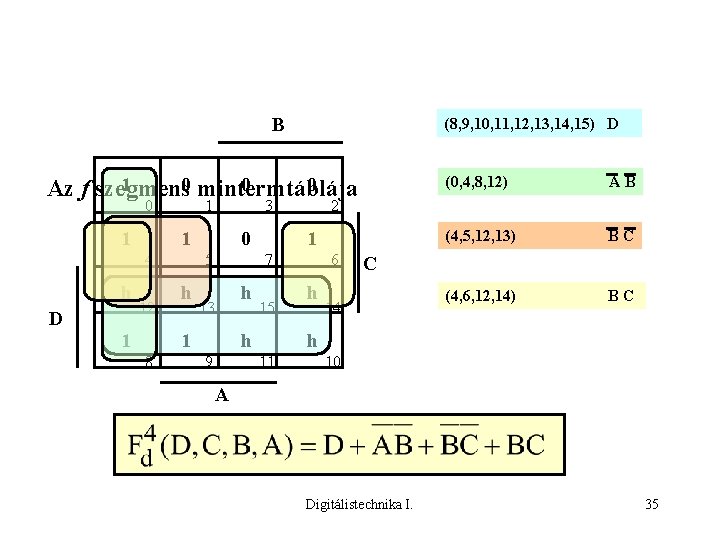
B (8, 9, 10, 11, 12, 13, 14, 15) D 1 0 mintermtáblája 0 0 Az f szegmens 0 1 1 1 4 h D 3 12 1 0 5 h 13 1 8 1 15 h 9 AB (4, 5, 12, 13) BC (4, 6, 12, 14) BC 2 7 h (0, 4, 8, 12) 6 h C 14 h 11 10 A Digitálistechnika I. 35

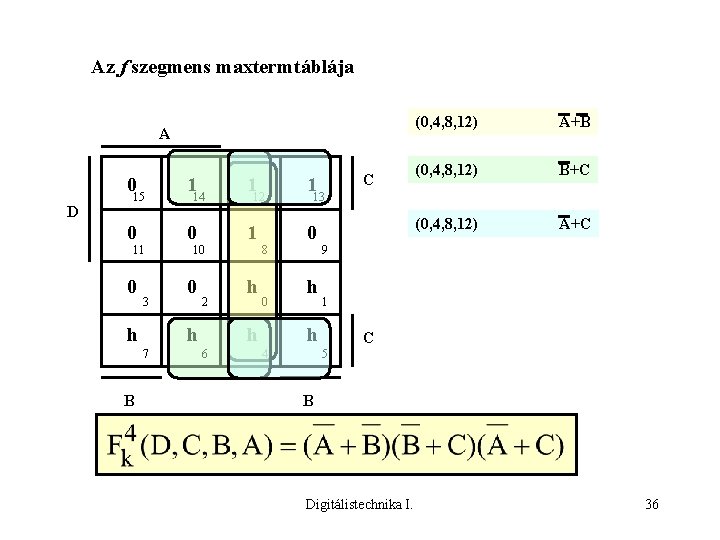
Az f szegmens maxtermtáblája A D 015 114 112 113 0 0 11 0 3 h 0 2 h 7 B 10 h 8 0 h 6 h A+B (0, 4, 8, 12) B+C (0, 4, 8, 12) A+C 9 1 h 4 C (0, 4, 8, 12) C 5 B Digitálistechnika I. 36

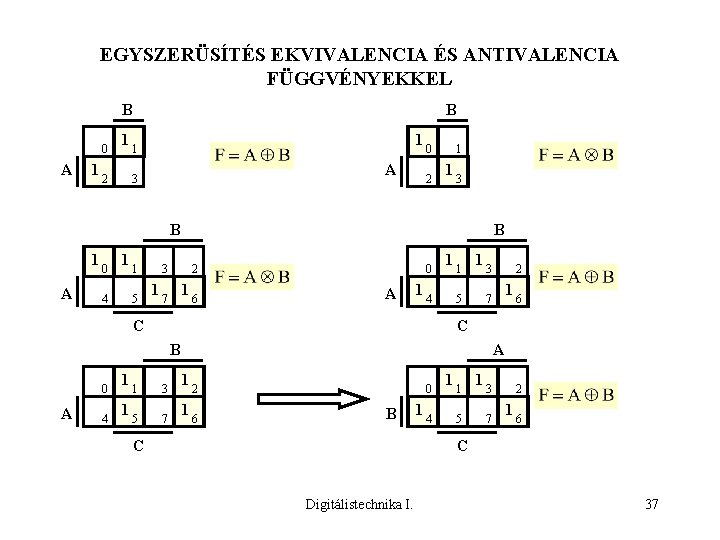
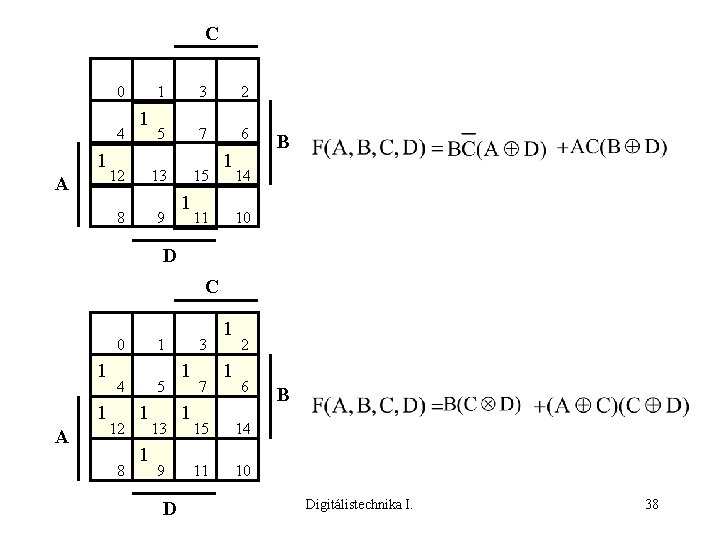
EGYSZERÜSÍTÉS EKVIVALENCIA ÉS ANTIVALENCIA FÜGGVÉNYEKKEL B 0 A 1 1 2 B 1 1 A 3 0 2 1 1 3 B 1 A 0 1 4 1 5 B 3 1 2 1 7 6 0 A 1 1 4 1 1 5 C 3 A 4 1 1 1 7 6 C B 0 2 1 3 5 7 A 1 1 2 6 0 B C 1 4 1 1 5 1 3 7 2 1 6 C Digitálistechnika I. 37

C 0 4 1 A 1 1 3 2 5 7 6 12 13 8 9 15 1 1 11 B 14 10 D C 0 1 1 A 1 4 12 8 5 1 1 13 9 D 3 1 1 7 1 1 2 6 15 14 11 10 B Digitálistechnika I. 38

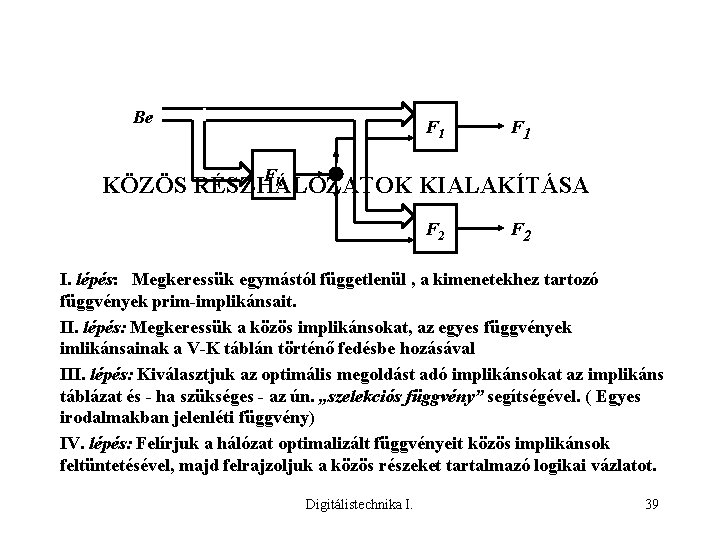
Be F 1 F k KÖZÖS RÉSZHÁLÓZATOK KIALAKÍTÁSA F 2 I. lépés: Megkeressük egymástól függetlenül , a kimenetekhez tartozó függvények prim-implikánsait. II. lépés: Megkeressük a közös implikánsokat, az egyes függvények imlikánsainak a V-K táblán történő fedésbe hozásával III. lépés: Kiválasztjuk az optimális megoldást adó implikánsokat az implikáns táblázat és - ha szükséges - az ún. „szelekciós függvény” segítségével. ( Egyes irodalmakban jelenléti függvény) IV. lépés: Felírjuk a hálózat optimalizált függvényeit közös implikánsok feltüntetésével, majd felrajzoljuk a közös részeket tartalmazó logikai vázlatot. Digitálistechnika I. 39

PÉLDA KÖZÖS RÉSZHÁLÓZAT KIALAKÍTÁSÁRA B B 0 1 4 1 D 12 8 1 1 5 7 13 1 3 15 1 9 11 2 1 6 1 0 C D 10 B A 0 1 1 3 2 5 7 6 12 13 15 14 8 1 1 9 11 3 2 5 7 6 12 13 15 14 1 8 1 1 9 11 C 10 A 4 1 D 1 1 1 4 1 14 1 C 10 A Digitálistechnika I. 40

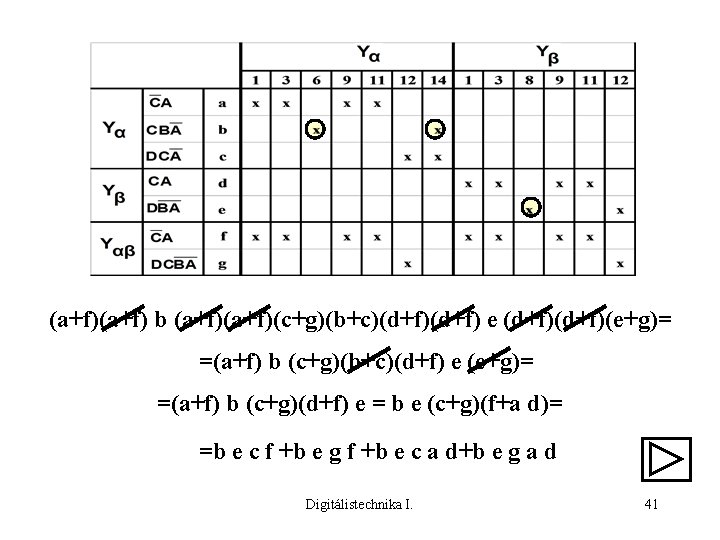
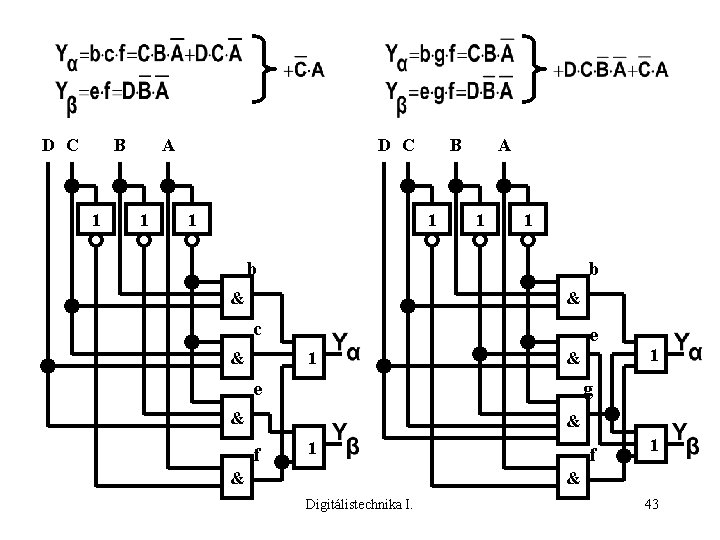
(a+f) b (a+f)(c+g)(b+c)(d+f) e (d+f)(e+g)= =(a+f) b (c+g)(b+c)(d+f) e (e+g)= =(a+f) b (c+g)(d+f) e = b e (c+g)(f+a d)= =b e c f +b e g f +b e c a d+b e g a d Digitálistechnika I. 41

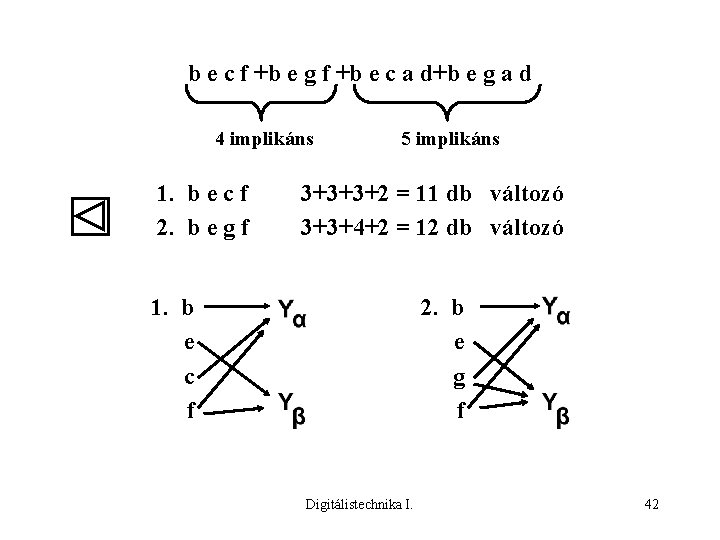
b e c f +b e g f +b e c a d+b e g a d 4 implikáns 1. b e c f 2. b e g f 5 implikáns 3+3+3+2 = 11 db változó 3+3+4+2 = 12 db változó 1. b e c f 2. b e g f Digitálistechnika I. 42

D C B 1 A 1 D C 1 B 1 A 1 1 b b & & c & e 1 g & & f 1 & Digitálistechnika I. 43

6. ELŐADÁS NUMERIKUS MINIMALIZÁLÁS • A TERMEK ÖSSZEVONÁSÁNAK KRITÉRIUMAI • A MINIMALIZÁLÁS LÉPÉSEI • PRIMIMPLIKÁNS TÁBLÁZAT Digitálistechnika I. 44

A TERMEK ÖSSZEVONÁSÁNAK KRITÉRIUMAI: NUMERIKUS MINIMALIZÁLÁS CLUSKEY MÓDSZER 1 A bináris. QUINE súlyok Mc különbsége 1 kell hogy legyen (bináris súly = a termben szereplő „egyesek” száma) 2 A decimális indexek különbsége kettő hatványa kell legyen 3 A nagyobb bináris súlyúnak a decimális indexe is nagyobb kell legyen Digitálistechnika I. 45

1 A Termeket bináris súlyuknak megfelelően csoportosítjuk a decimális indexek növekvő sorrendjében 2 Az összehasonlítást a legelső elemmel kezdjük, ezt csak a következő csoport A MINIMALIZÁLÁS LÉPÉSEI elemeivel kell összehasonlítani. Ha találunk olyan számpát amely kielégíti a „ 2” -es és „ 3” -as feltételt, akkor mindkettőt megjelöljük, és a számpár elemeit növekvő sorrendbenegy új oszlopba egymás mellé írjuk, majd zárójelben megjelöljük a különbségüket is. 3 A második oszlopból a harmadik oszlopot az előző pontban leírt módon képezzük, de az összevonás feltétele az, hogy a zárójelben lévő összes szám megegyezzen, és ugyanazon változók hiányozzanak mindkét csoportból, és az első decimális számok különbsége 2 pozitív egész kitevőjű hatványa legyen, és a hátrább álló csoportból való decimális szám legyen a nagyobb. A nem jelölt csoportok a primimplikánsok 4 A szükséges primimplikánsok kiválastása a primimplikáns táblázattal történik Digitálistechnika I. 46

Bináris súly I. oszlop 3 2 2 3 3 9 10 12 7 11 13 14 15 + + + + II. oszlop 9, 11 (2) 9, 13 (4) 10, 11 (1) 10, 14 (4) 12, 13 (1) 12, 14 (2) 7, 15 (8) 11, 15 (4) 13, 15 (2) 14, 15 (1) III. oszlop + 9, 11, 13, 15 (2, 4) b + 10, 11, 14, 15 (1, 4) c + 12, 13, 14, 15 (1, 2) d + + + a + + + 4 Digitálistechnika I. 47

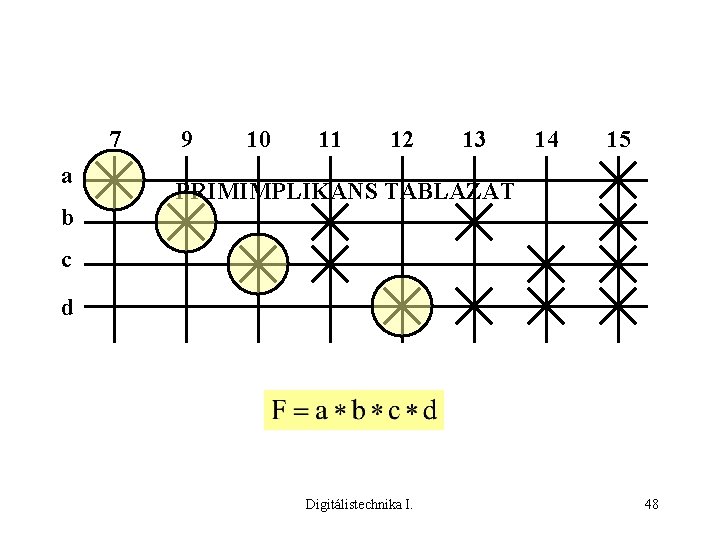
7 a b 9 10 11 12 13 14 15 PRIMIMPLIKÁNS TÁBLÁZAT c d Digitálistechnika I. 48

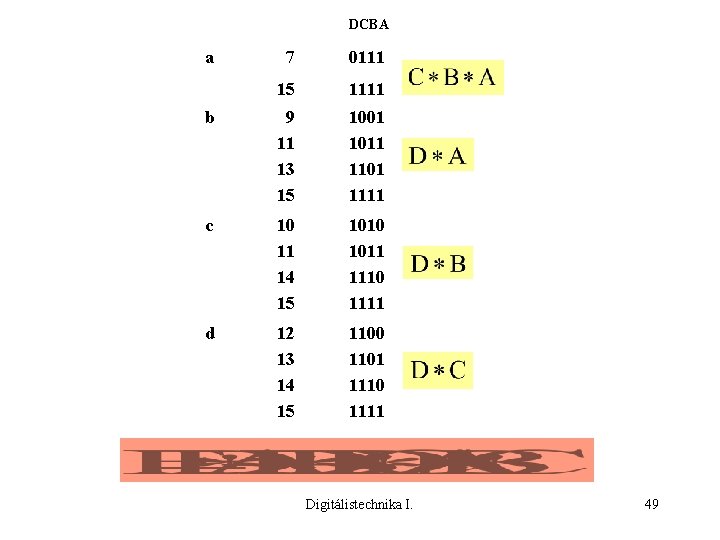
DCBA a 7 0111 15 1111 b 9 11 13 15 1001 1011 1101 1111 c 10 11 14 15 1010 1011 1110 1111 d 12 13 14 15 1100 1101 1110 1111 Digitálistechnika I. 49

7. ELŐADÁS LOGIKAI FÜGGVÉNYEK REALIZÁLÁSA • KONTAKTUSOKKAL • KAPUÁRAMKÖRÖKKEL • KAPUK BŐVÍTÉSE • FUNKCIONÁLISAN TELJES RENDSZEREK Digitálistechnika I. 50

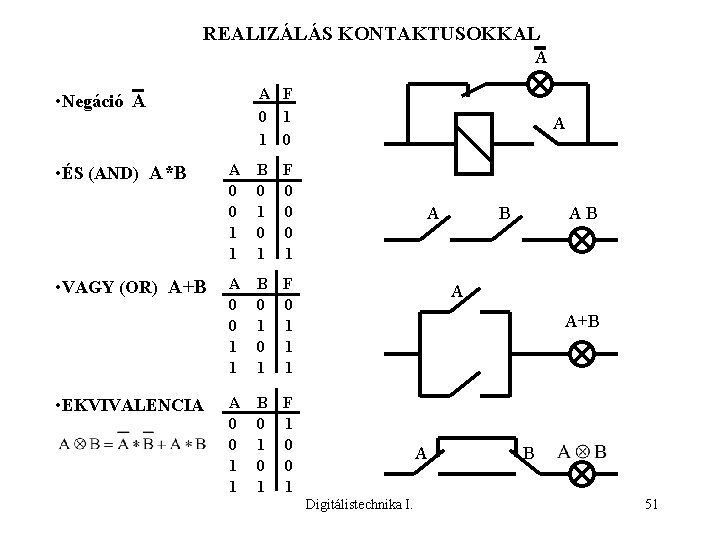
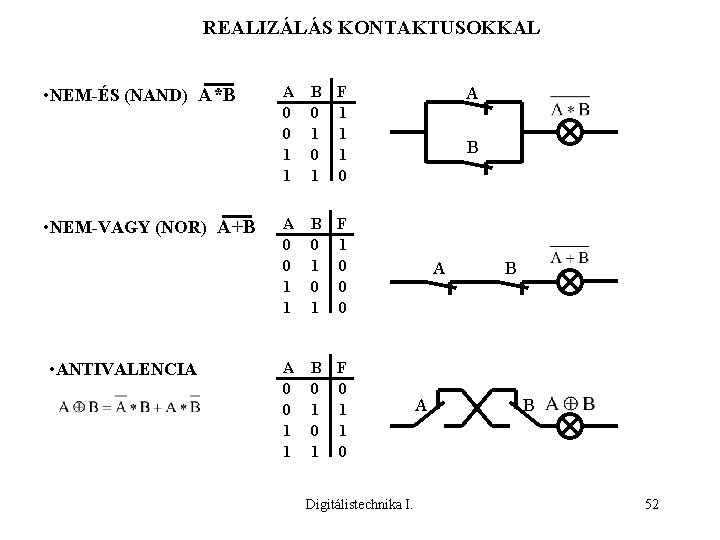
REALIZÁLÁS KONTAKTUSOKKAL A A F 0 1 1 0 • Negáció A • ÉS (AND) A*B • VAGY (OR) A+B • EKVIVALENCIA A 0 0 1 1 B F 0 0 1 0 0 0 1 1 A 0 0 1 1 B F 0 0 1 1 1 A 0 0 1 1 B F 0 1 1 0 0 0 1 1 A A B AB A A+B A Digitálistechnika I. B 51

REALIZÁLÁS KONTAKTUSOKKAL • NEM-ÉS (NAND) A*B • NEM-VAGY (NOR) A+B • ANTIVALENCIA A 0 0 1 1 B F 0 1 1 1 0 A 0 0 1 1 B F 0 1 1 0 0 0 1 0 A 0 0 1 1 B F 0 0 1 1 0 Digitálistechnika I. A B A A B B 52

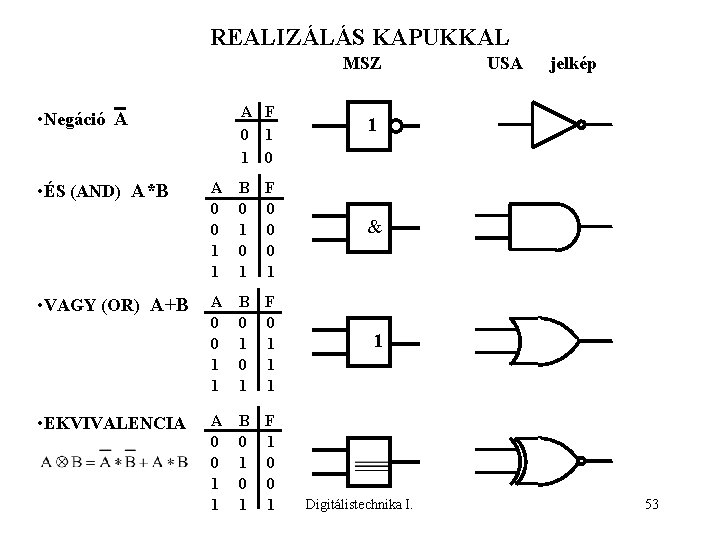
REALIZÁLÁS KAPUKKAL MSZ A F 0 1 1 0 • Negáció A • ÉS (AND) A*B • VAGY (OR) A+B • EKVIVALENCIA USA jelkép 1 A 0 0 1 1 B 0 1 F 0 0 0 1 & A 0 0 1 1 B 0 1 F 0 1 1 A 0 0 1 1 B 0 1 F 1 0 0 1 Digitálistechnika I. 53

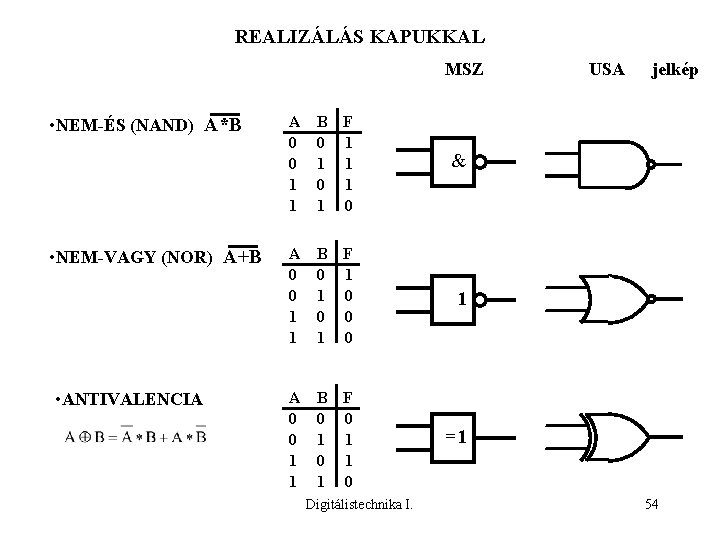
REALIZÁLÁS KAPUKKAL MSZ • NEM-ÉS (NAND) A*B • NEM-VAGY (NOR) A+B • ANTIVALENCIA A 0 0 1 1 B F 0 1 1 1 0 & A 0 0 1 1 B F 0 1 1 0 0 0 1 A 0 0 1 1 B F 0 0 1 1 0 =1 Digitálistechnika I. USA jelkép 54

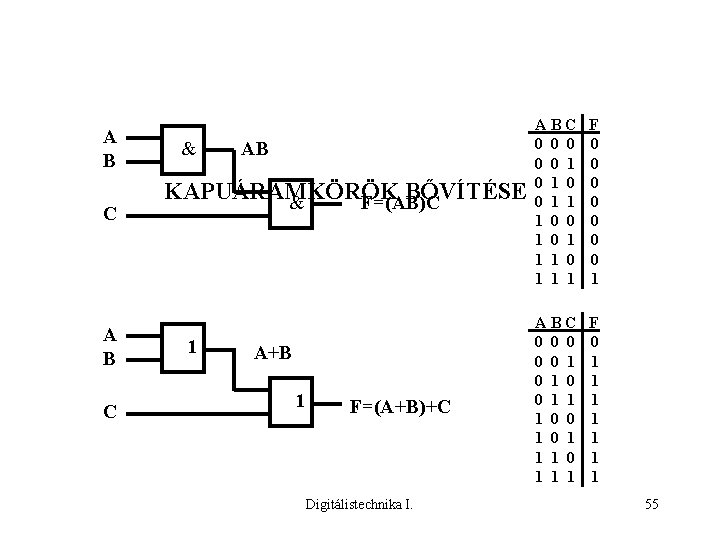
A B C & AB KAPUÁRAMKÖRÖK BŐVÍTÉSE & F=(AB)C 1 A+B 1 F=(A+B)+C Digitálistechnika I. ABC 0 0 0 1 1 1 0 0 1 1 1 F 0 0 0 0 1 ABC 0 0 0 1 1 1 0 0 1 1 1 F 0 1 1 1 1 55

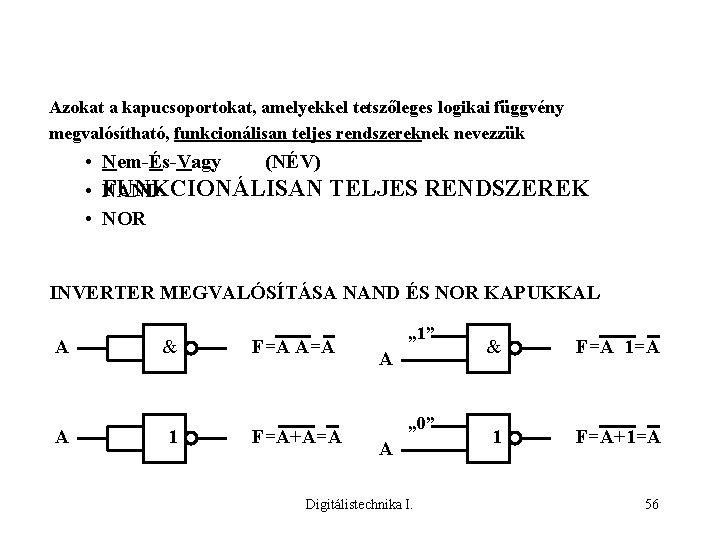
Azokat a kapucsoportokat, amelyekkel tetszőleges logikai függvény megvalósítható, funkcionálisan teljes rendszereknek nevezzük • Nem-És-Vagy (NÉV) TELJES RENDSZEREK • FUNKCIONÁLISAN NAND • NOR INVERTER MEGVALÓSÍTÁSA NAND ÉS NOR KAPUKKAL A & F=A A 1 F=A+A=A „ 1” A „ 0” A Digitálistechnika I. & F=A 1 F=A+1=A 56

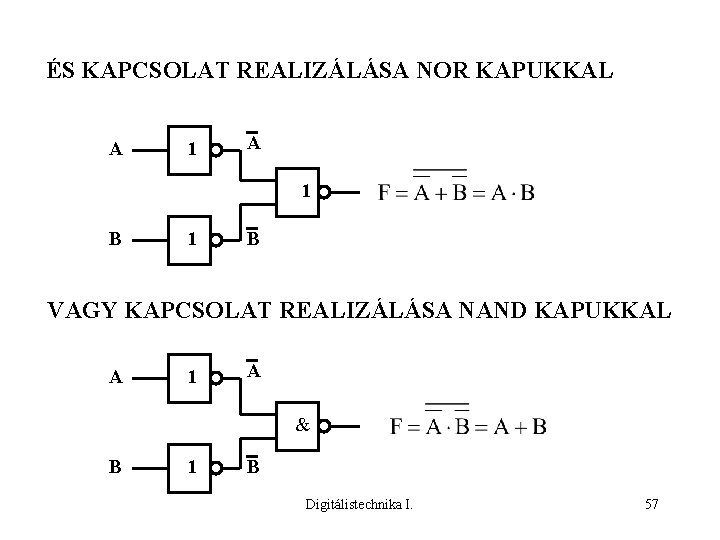
ÉS KAPCSOLAT REALIZÁLÁSA NOR KAPUKKAL A 1 B 1 B VAGY KAPCSOLAT REALIZÁLÁSA NAND KAPUKKAL A 1 A & B 1 B Digitálistechnika I. 57

8. ELŐADÁS LOGIKAI FÜGGVÉNYEK KÉTSZINTŰ REALIZÁLÁSA • • • KAPU TRANSZFORMÁCIÓK KÉTSZINTŰ REALIZÁLÁSI LEHETŐSÉGEK REALIZÁLÁS N-É-V RENDSZERBEN REALIZÁLÁS NAND ÉS NOR RENDSZERBEN REALIZÁLÁS ELŐTT FIGYELEMBE VEENDŐ SZEMPONTOK Digitálistechnika I. 58

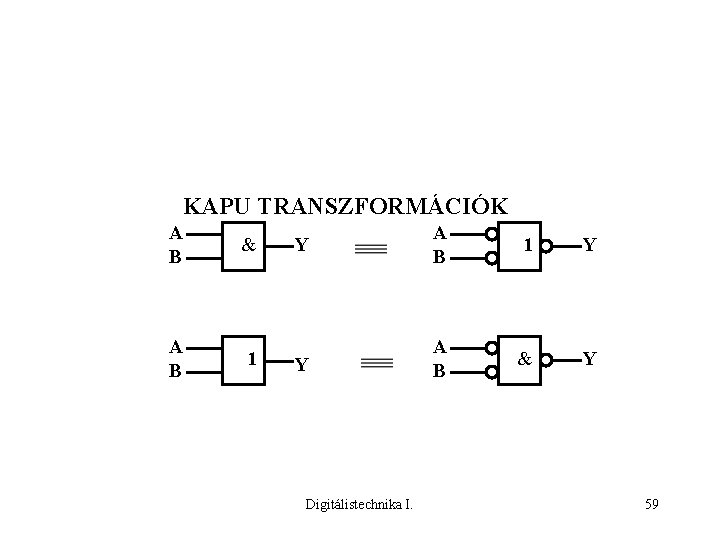
KAPU TRANSZFORMÁCIÓK A B & A B 1 Y Y A B & Y Digitálistechnika I. 59

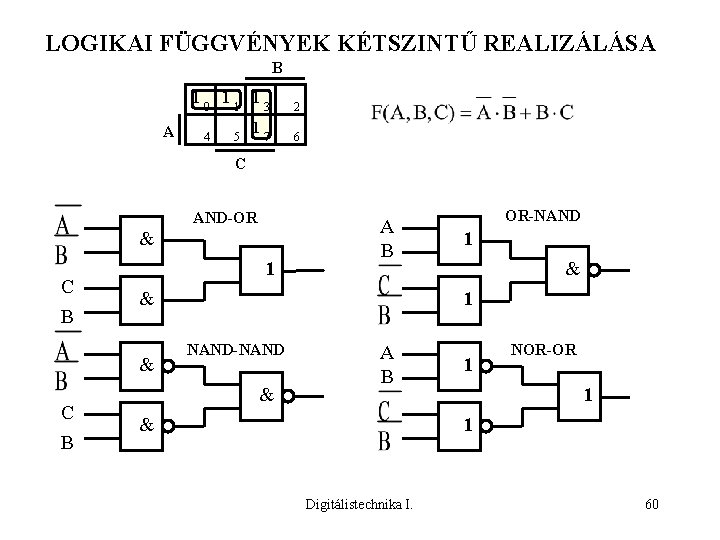
LOGIKAI FÜGGVÉNYEK KÉTSZINTŰ REALIZÁLÁSA B 1 A 0 4 1 1 5 1 1 3 2 7 6 C AND-OR & C B 1 OR-NAND 1 & & C B A B NAND-NAND & A B 1 NOR-OR 1 1 & Digitálistechnika I. 60

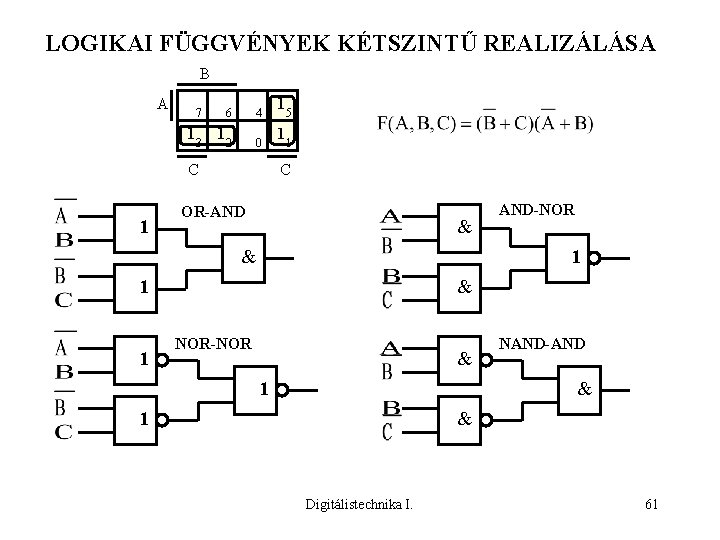
LOGIKAI FÜGGVÉNYEK KÉTSZINTŰ REALIZÁLÁSA B A 7 1 3 1 6 4 2 0 C 1 1 1 5 1 C OR-AND & 1 1 AND-NOR & NOR-NOR & 1 NAND-AND & 1 & Digitálistechnika I. 61

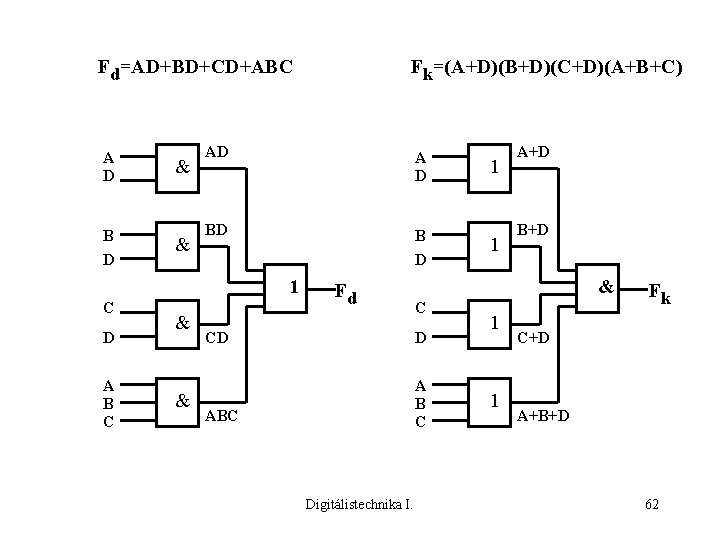
Fd=AD+BD+CD+ABC A D B D & & AD A D BD B D 1 C D A B C & & Fk=(A+D)(B+D)(C+D)(A+B+C) Fd 1 B+D & C CD D ABC A B C Digitálistechnika I. 1 A+D 1 1 Fk C+D A+B+D 62

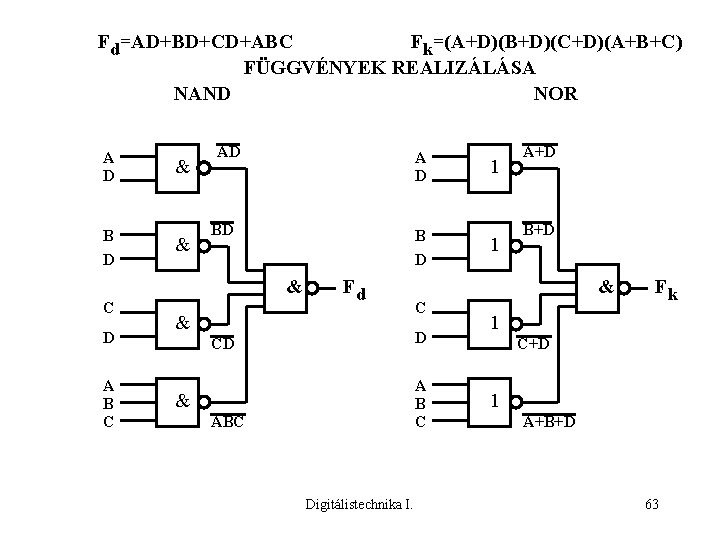
Fd=AD+BD+CD+ABC Fk=(A+D)(B+D)(C+D)(A+B+C) FÜGGVÉNYEK REALIZÁLÁSA NAND NOR A D B D & & AD A D BD B D & C D A B C Fd & C CD ABC A B C Digitálistechnika I. 1 B+D & 1 A+D Fk 1 C+D 1 A+B+D 63

A REALIZÁLÁS ELŐTT FIGYELEMBE VEENDŐ SZEMPONTOK • FOGYASZTÁS – áramkörcsalád (TTL, MOS, ECL, stb. ) – tokszám • HELYFOGLALÁS – tokozat (hagyományos, SMD) – tokszám • KÉSLELTETÉSI IDŐ – áramkörcsalád (TTL, MOS, ECL, stb. ) – alkalmazott szintek száma KÖVETKEZTETÉS: A legkedvezőbb megoldást kétszintű realizálás esetén, minimális tokszám mellett kapjuk Digitálistechnika I. 64

1 BEMENEŰ KAPU (INVERTER) 6 db 2 BEMENETŰ KAPU (AND, NAND, OR, NOR, XOR) 4 db 3 BEMENETŰ KAPU (AND, NAND, OR, NOR) 3 db 4 BEMENETŰ KAPU 2 db EGY TOKBAN TALÁLHATÓ KAPUKSZÁMA Digitálistechnika I. 65

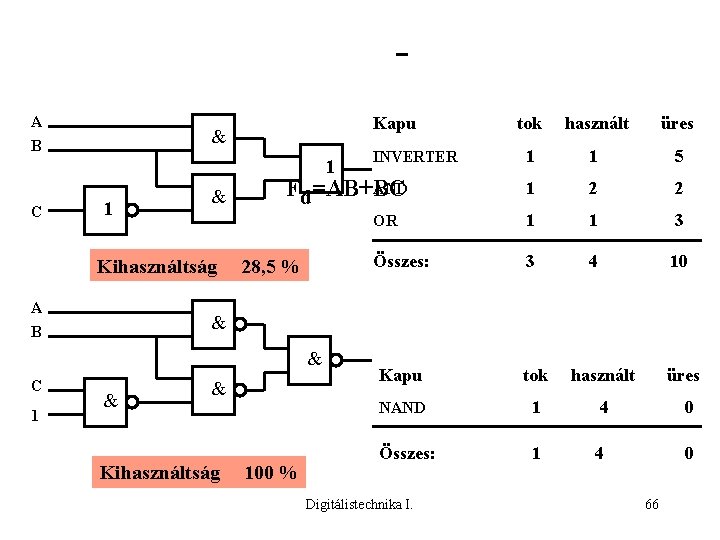
A B Kapu & 1 C 1 & Kihasználtság A B 1 használt üres 1 1 5 1 2 2 OR 1 1 3 Összes: 3 4 10 Kapu tok használt NAND 1 4 0 Összes: 1 4 0 INVERTER AND Fd=AB+BC 28, 5 % & & C tok & & Kihasználtság 100 % Digitálistechnika I. üres 66

9. ELŐADÁS A KAPUK KÉSLELTETŐ HATÁSÁNAK FIGYELEMBEVÉTELE • KAPUKÉSLELTETÉS • STATIKUS HAZÁRD • HAZÁRDMENTESÍTÉS • EGYÉB HAZÁRDOK Digitálistechnika I. 67

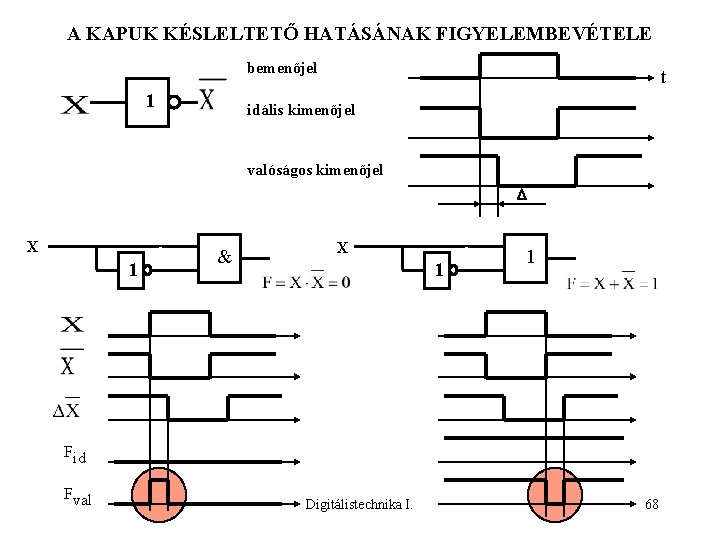
A KAPUK KÉSLELTETŐ HATÁSÁNAK FIGYELEMBEVÉTELE bemenőjel 1 t idális kimenőjel valóságos kimenőjel X 1 & X 1 1 Fid Fval Digitálistechnika I. 68

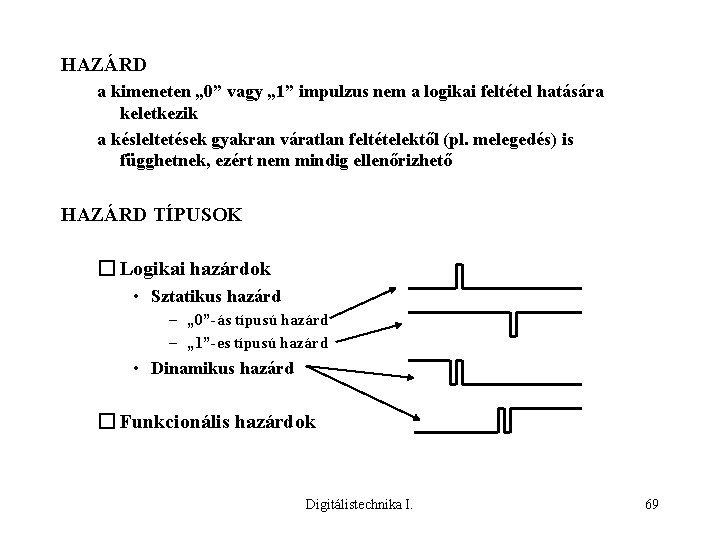
HAZÁRD a kimeneten „ 0” vagy „ 1” impulzus nem a logikai feltétel hatására keletkezik a késleltetések gyakran váratlan feltételektől (pl. melegedés) is függhetnek, ezért nem mindig ellenőrizhető HAZÁRD TÍPUSOK � Logikai hazárdok • Sztatikus hazárd – „ 0”-ás típusú hazárd – „ 1”-es típusú hazárd • Dinamikus hazárd � Funkcionális hazárdok Digitálistechnika I. 69

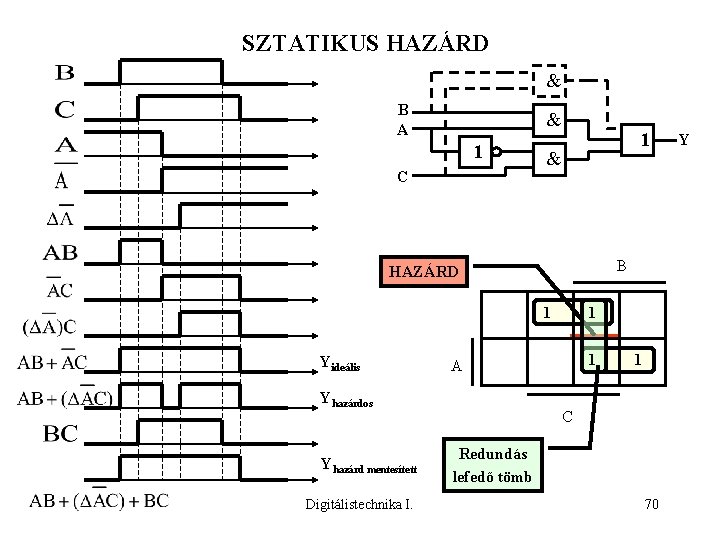
SZTATIKUS HAZÁRD & B A & 1 C 1 & B HAZÁRD 1 Yideális Digitálistechnika I. 1 A Yhazárdos Yhazárd mentesített 1 1 C Redundás lefedő tömb 70 Y

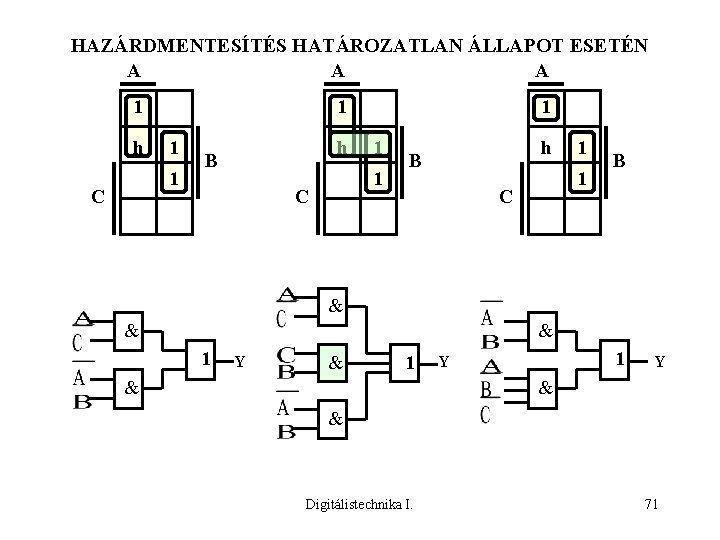
HAZÁRDMENTESÍTÉS HATÁROZATLAN ÁLLAPOT ESETÉN A A A 1 h 1 1 1 C h B 1 1 C B & & & 1 Y & 1 1 Y Y & & & Digitálistechnika I. 71

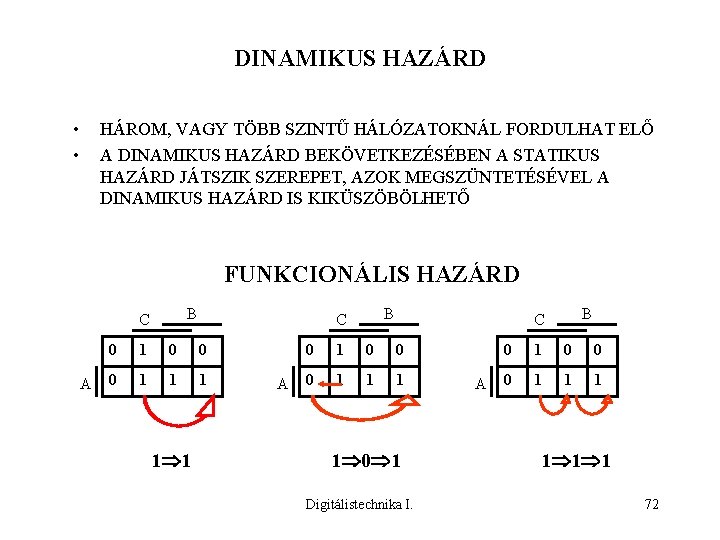
DINAMIKUS HAZÁRD • • HÁROM, VAGY TÖBB SZINTŰ HÁLÓZATOKNÁL FORDULHAT ELŐ A DINAMIKUS HAZÁRD BEKÖVETKEZÉSÉBEN A STATIKUS HAZÁRD JÁTSZIK SZEREPET, AZOK MEGSZÜNTETÉSÉVEL A DINAMIKUS HAZÁRD IS KIKÜSZÖBÖLHETŐ FUNKCIONÁLIS HAZÁRD B C A 0 1 0 0 0 1 1 1 B C A B C 0 1 0 0 0 1 1 0 1 Digitálistechnika I. A 0 1 0 0 0 1 1 1 72

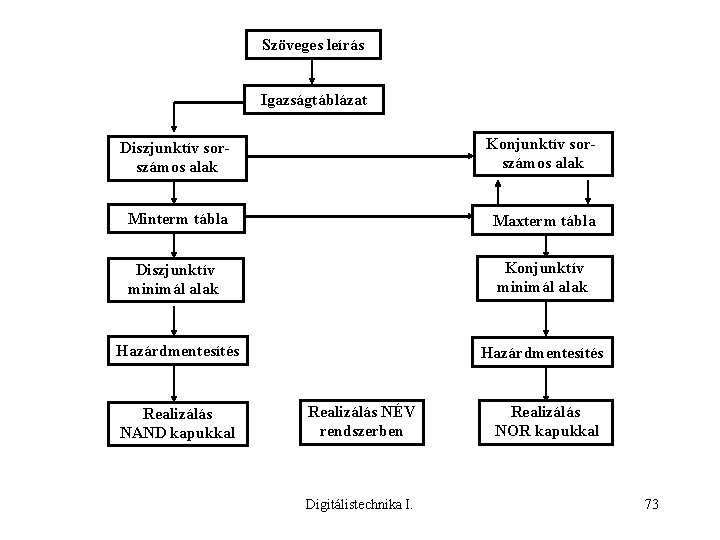
Szöveges leírás Igazságtáblázat Diszjunktív sorszámos alak Konjunktív sorszámos alak Minterm tábla Maxterm tábla Diszjunktív minimál alak Konjunktív minimál alak Hazárdmentesítés Realizálás NAND kapukkal Realizálás NÉV rendszerben Digitálistechnika I. Realizálás NOR kapukkal 73

10. ELŐADÁS FUNKCIONÁLIS EGYSÉGEK I. • MULTIPLEXEREK BŐVÍTÉSE • LOGIKAI FÜGGVÉNYEK REALIZÁLÁSA MULTIPLEXERREL • DEMULTIPLEXEREK BŐVÍTÉSE • KÓDÁTALAKÍTÓK Digitálistechnika I. 74

FUNKCIONÁLIS EGYSÉGEK A funkcionális egységek valamely komplex feladatra kialakított, rendszerint moduláris szempontokat is figyelembevevő összetett elektronikus hálózatok FUNKCIONÁLIS EGYSÉGEK • Kombinációs hálózatokra épülő egységek – – multiplexerek/demultiplexerek kódolók/dekódolók összeadók komparátorok • Szekvenciális hálózatokra épülő egységek – flip-flop-ok – regiszterek – számlálók • Memóriák – ROM – RAM • A/D és D/A átalakítók Digitálistechnika I. 75

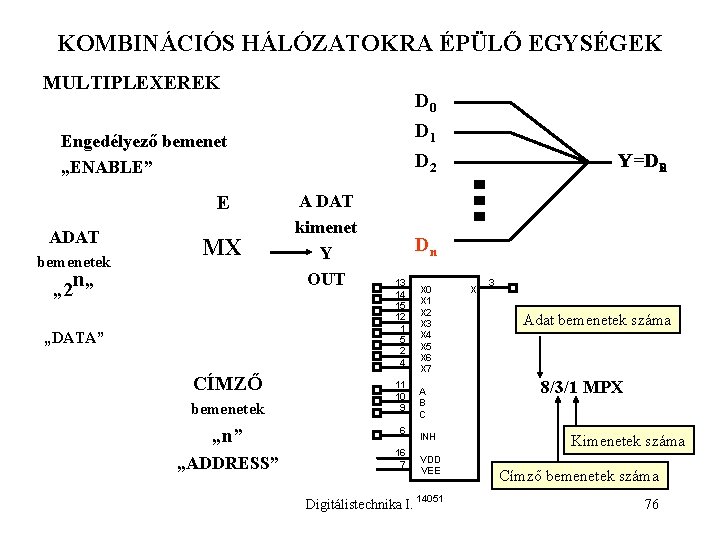
KOMBINÁCIÓS HÁLÓZATOKRA ÉPÜLŐ EGYSÉGEK MULTIPLEXEREK D 0 D 1 Engedélyező bemenet „ENABLE” E ADAT bemenetek MX „ 2 n” „DATA” CÍMZŐ bemenetek „n” „ADDRESS” Y=D 1 n 20 D 2 A DAT kimenet Y OUT Dn 13 14 15 12 1 5 2 4 11 10 9 6 16 7 Digitálistechnika I. X 0 X 1 X 2 X 3 X 4 X 5 X 6 X 7 A B C INH VDD VEE 14051 X 3 Adat bemenetek száma 8/3/1 MPX Kimenetek száma Címző bemenetek száma 76

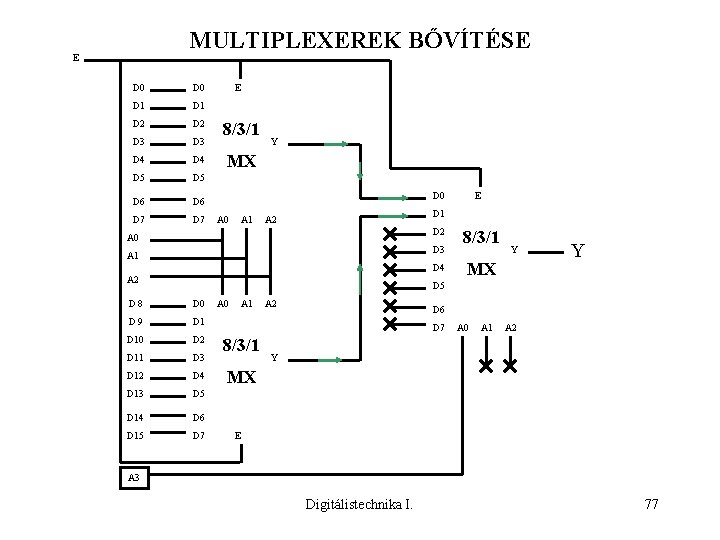
MULTIPLEXEREK BŐVÍTÉSE E D 0 D 1 D 2 D 3 D 4 D 5 D 6 D 7 E 8/3/1 Y MX D 0 A 1 E D 1 A 2 D 2 A 0 D 3 A 1 D 4 A 2 8/3/1 Y MX Y D 5 D 8 D 0 D 9 D 10 D 2 D 11 D 3 D 12 D 4 D 13 D 5 D 14 D 6 D 15 D 7 A 0 A 1 A 2 D 6 D 7 8/3/1 A 0 A 1 A 2 Y MX E A 3 Digitálistechnika I. 77

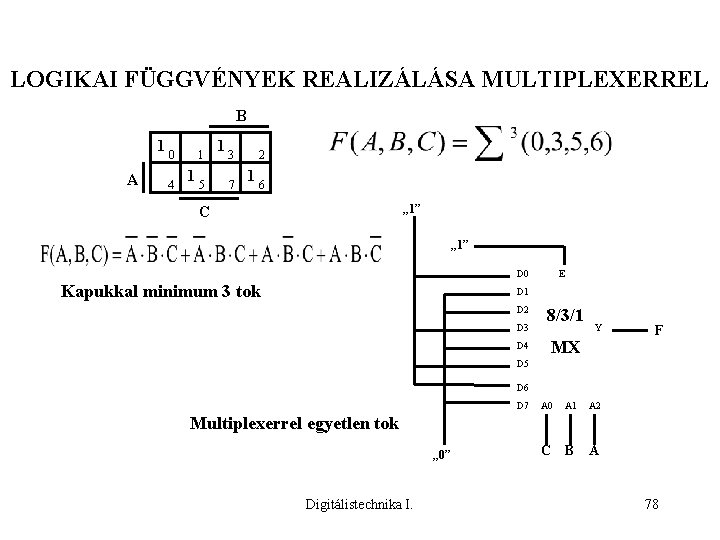
LOGIKAI FÜGGVÉNYEK REALIZÁLÁSA MULTIPLEXERREL B 1 A 0 4 1 1 5 1 3 7 2 1 6 „ 1” C „ 1” D 0 Kapukkal minimum 3 tok E D 1 D 2 D 3 D 4 8/3/1 Y MX F D 5 D 6 D 7 A 0 A 1 A 2 C B A Multiplexerrel egyetlen tok „ 0” Digitálistechnika I. 78

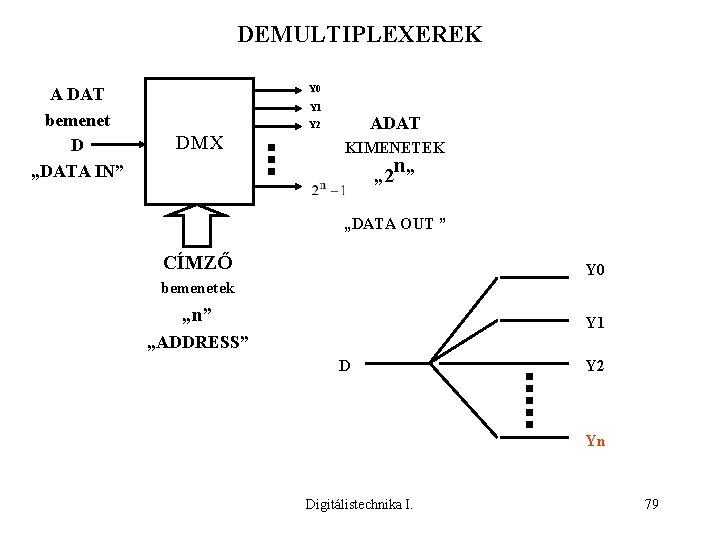
DEMULTIPLEXEREK A DAT bemenet D „DATA IN” Y 0 Y 1 ADAT Y 2 DMX KIMENETEK „ 2 n” „DATA OUT ” CÍMZŐ Y 0 bemenetek „n” Y 1 „ADDRESS” D Y 2 Yn Digitálistechnika I. 79

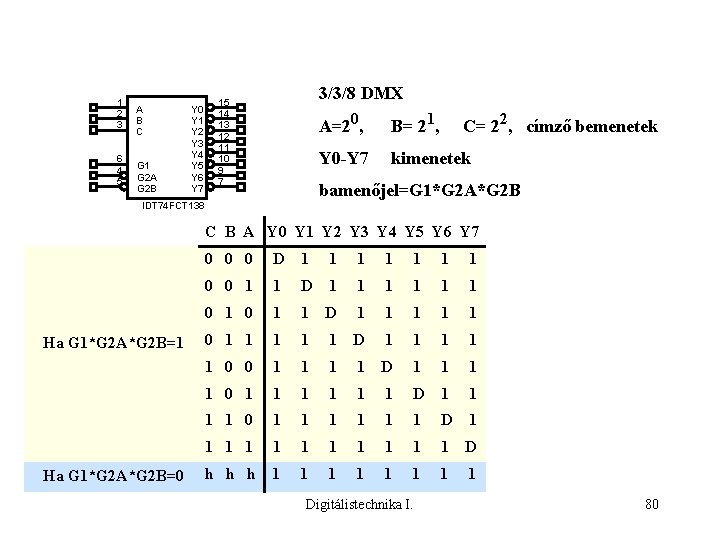
1 2 3 6 4 5 A B C G 1 G 2 A G 2 B Y 0 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7 3/3/8 DMX 15 14 13 12 11 10 9 7 A=20, B= 21, C= 22, címző bemenetek Y 0 -Y 7 kimenetek bamenőjel=G 1*G 2 A*G 2 B IDT 74 FCT 138 C B A Y 0 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7 Ha G 1*G 2 A*G 2 B=1 Ha G 1*G 2 A*G 2 B=0 0 D 1 1 1 1 0 0 1 1 D 1 1 1 0 1 1 1 D 1 1 1 0 0 1 1 1 1 D 1 1 1 1 1 1 D h h h 1 1 1 1 Digitálistechnika I. 80

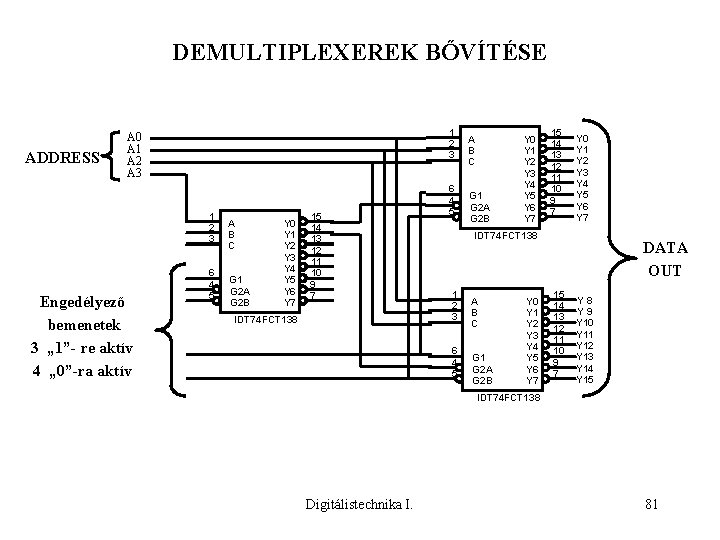
DEMULTIPLEXEREK BŐVÍTÉSE ADDRESS 1 2 3 A 0 A 1 A 2 A 3 1 2 3 Engedélyező bemenetek 3 „ 1”- re aktív 4 „ 0”-ra aktív 6 4 5 A B C G 1 G 2 A G 2 B Y 0 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7 15 14 13 12 11 10 9 7 IDT 74 FCT 138 6 4 5 A B C G 1 G 2 A G 2 B Y 0 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7 15 14 13 12 11 10 9 7 Y 0 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7 IDT 74 FCT 138 1 2 3 6 4 5 A B C G 1 G 2 A G 2 B Y 0 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7 DATA OUT 15 14 13 12 11 10 9 7 Y 8 Y 9 Y 10 Y 11 Y 12 Y 13 Y 14 Y 15 IDT 74 FCT 138 Digitálistechnika I. 81

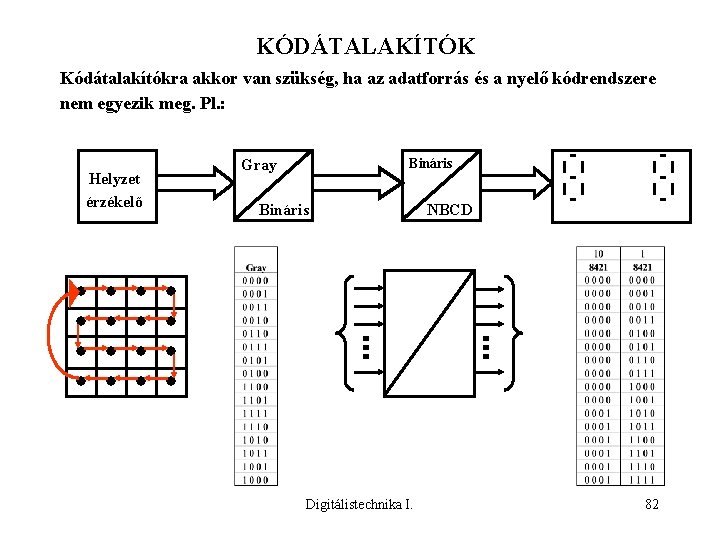
KÓDÁTALAKÍTÓK Kódátalakítókra akkor van szükség, ha az adatforrás és a nyelő kódrendszere nem egyezik meg. Pl. : Helyzet érzékelő Gray Bináris Digitálistechnika I. NBCD 82

11. ELŐADÁS FUNKCIONÁLIS EGYSÉGEK II. • • BINÁRIS ÖSSZEADÓK SOROS / PÁRHUZAMOS ÁTVITELKÉPZÉS BCD ÖSSZEADÓK KIVONÓK ARITMETIKAI LOGIKAI EGYSÉGEK • KOMPARÁTOROK BŐVÍTÉSE Digitálistechnika I. 83

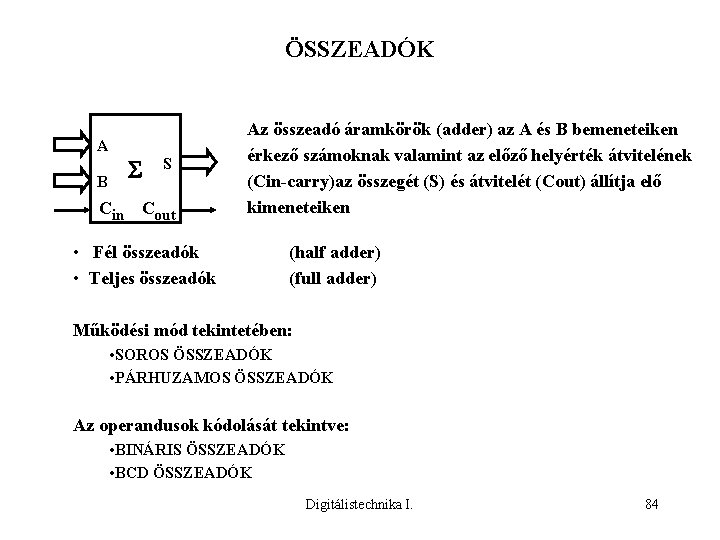
ÖSSZEADÓK A B S Cin Cout Az összeadó áramkörök (adder) az A és B bemeneteiken érkező számoknak valamint az előző helyérték átvitelének (Cin-carry)az összegét (S) és átvitelét (Cout) állítja elő kimeneteiken • Fél összeadók • Teljes összeadók (half adder) (full adder) Működési mód tekintetében: • SOROS ÖSSZEADÓK • PÁRHUZAMOS ÖSSZEADÓK Az operandusok kódolását tekintve: • BINÁRIS ÖSSZEADÓK • BCD ÖSSZEADÓK Digitálistechnika I. 84

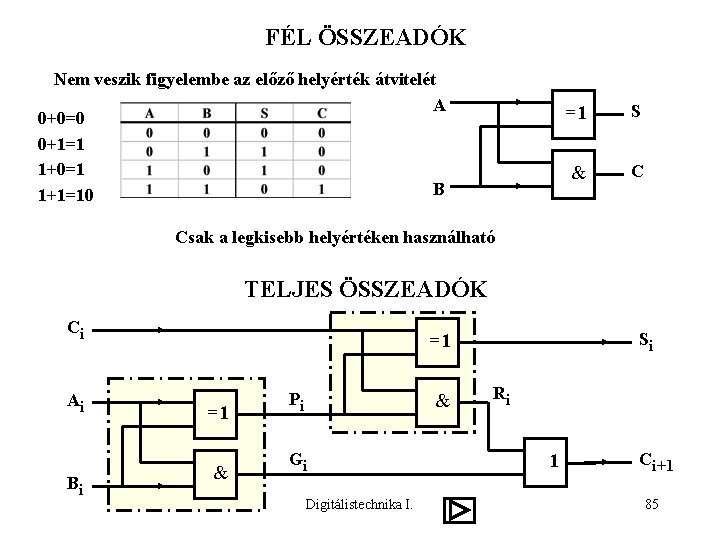
FÉL ÖSSZEADÓK Nem veszik figyelembe az előző helyérték átvitelét A 0+0=0 0+1=1 1+0=1 B 1+1=10 =1 S & C Csak a legkisebb helyértéken használható TELJES ÖSSZEADÓK Ci Ai Bi Si =1 =1 Pi & Gi & Digitálistechnika I. Ri 1 Ci+1 85

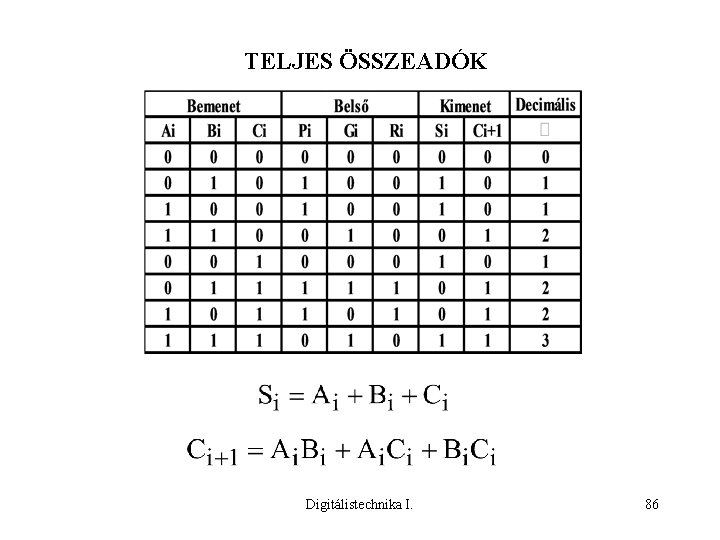
TELJES ÖSSZEADÓK Digitálistechnika I. 86

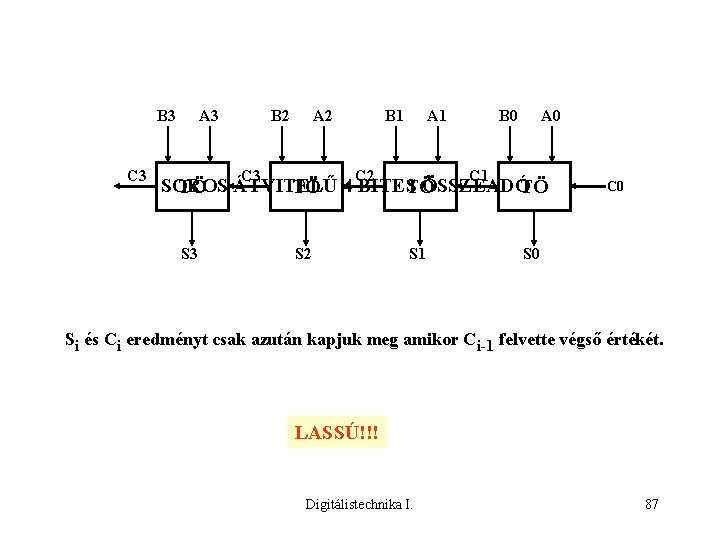
B 3 C 3 A 3 B 2 A 2 C 3 B 1 A 1 C 2 B 0 A 0 C 1 SOROS ÖSSZEADÓ TÖ ÁTVITELŰ TÖ 4 BITES TÖ TÖ S 3 S 2 S 1 C 0 Si és Ci eredményt csak azután kapjuk meg amikor Ci-1 felvette végső értékét. LASSÚ!!! Digitálistechnika I. 87

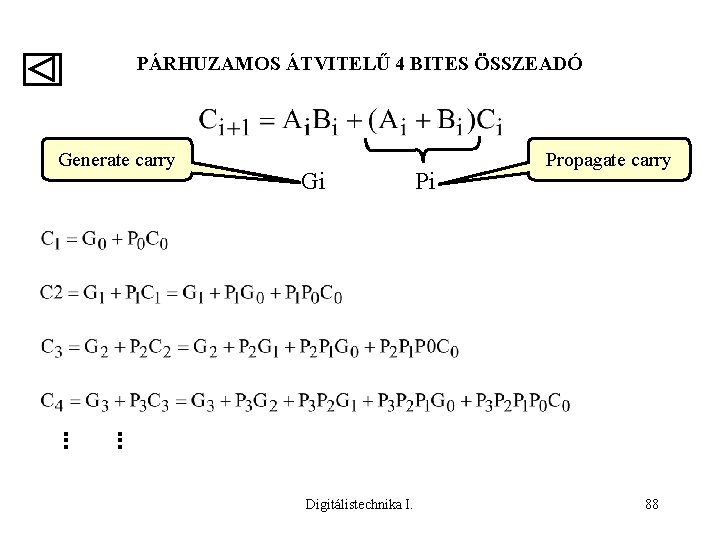
PÁRHUZAMOS ÁTVITELŰ 4 BITES ÖSSZEADÓ Keletkező Generate átvitel carry Gi Digitálistechnika I. Pi Propagate Terjedő átvitel carry 88

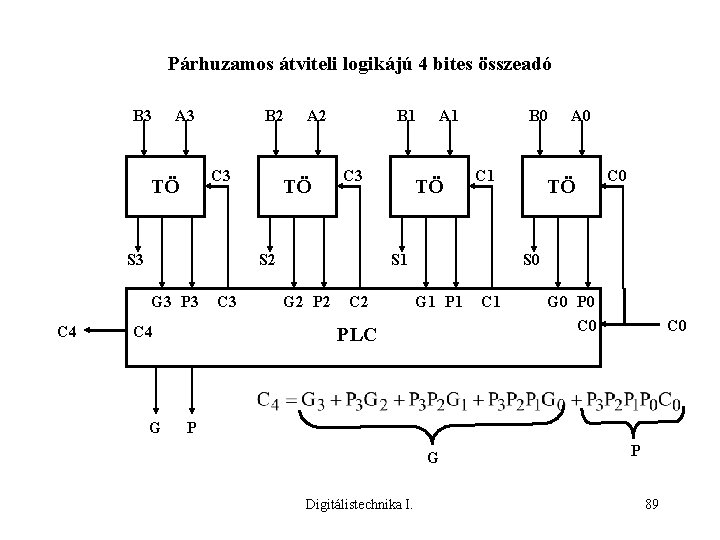
Párhuzamos átviteli logikájú 4 bites összeadó B 3 A 3 B 2 C 3 TÖ S 3 TÖ B 1 C 3 S 2 G 3 P 3 C 4 A 2 C 4 G C 3 B 0 A 1 TÖ C 1 S 1 G 2 P 2 C 2 A 0 C 0 TÖ S 0 G 1 P 1 C 1 G 0 P 0 C 0 PLC C 0 P G Digitálistechnika I. P 89

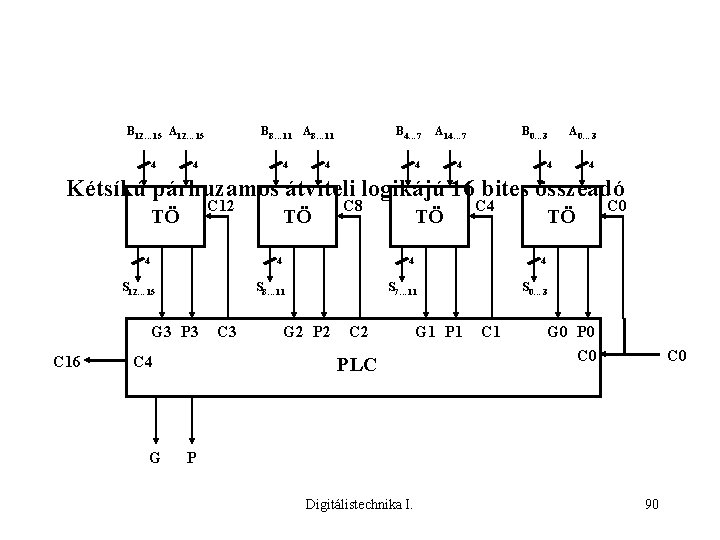
B 12… 15 A 12… 15 4 B 8… 11 A 8… 11 4 4 B 4… 7 4 A 14… 7 4 B 0… 3 4 A 0… 3 4 4 Kétsíkú párhuzamos átviteli logikájú 16 bites összeadó C 12 TÖ 4 C 8 4 S 12… 15 C 4 G C 3 TÖ C 4 4 S 8… 11 G 3 P 3 C 16 TÖ 4 S 7… 11 G 2 P 2 C 2 PLC C 0 TÖ G 1 P 1 S 0… 3 C 1 G 0 P 0 C 0 P Digitálistechnika I. 90

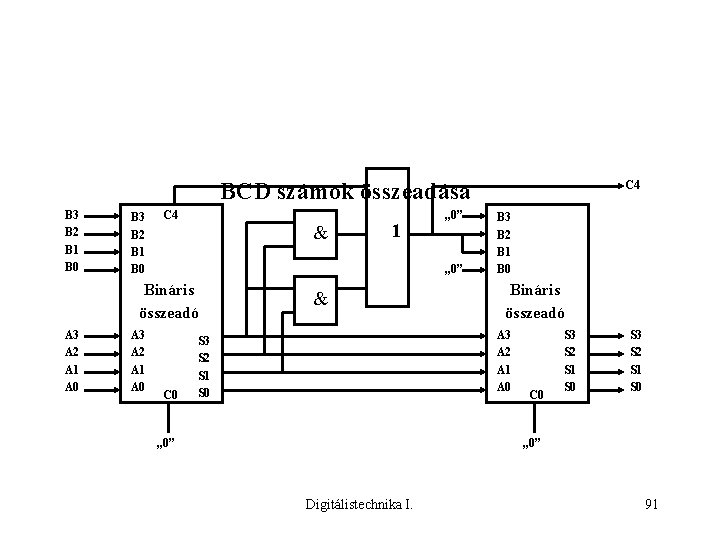
BCD számok összeadása B 3 B 2 B 1 B 0 C 4 & „ 0” Bináris összeadó A 3 A 2 A 1 A 0 1 „ 0” C 0 & C 4 B 3 B 2 B 1 B 0 Bináris összeadó A 3 A 2 A 1 A 0 S 3 S 2 S 1 S 0 „ 0” C 0 S 3 S 2 S 1 S 0 „ 0” Digitálistechnika I. 91

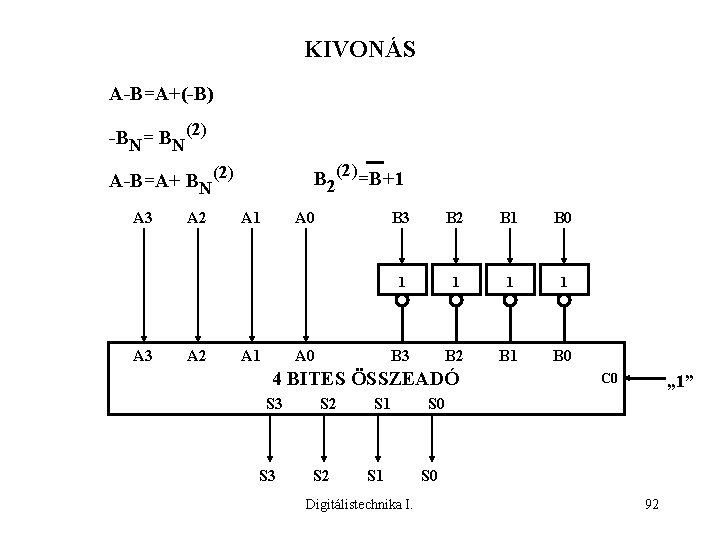
KIVONÁS A-B=A+(-B) -BN= BN(2) B 2(2)=B+1 A-B=A+ BN(2) A 3 A 2 A 1 A 0 B 3 B 2 B 1 B 0 1 1 B 3 B 2 B 1 B 0 4 BITES ÖSSZEADÓ S 3 S 2 S 1 Digitálistechnika I. C 0 „ 1” S 0 92

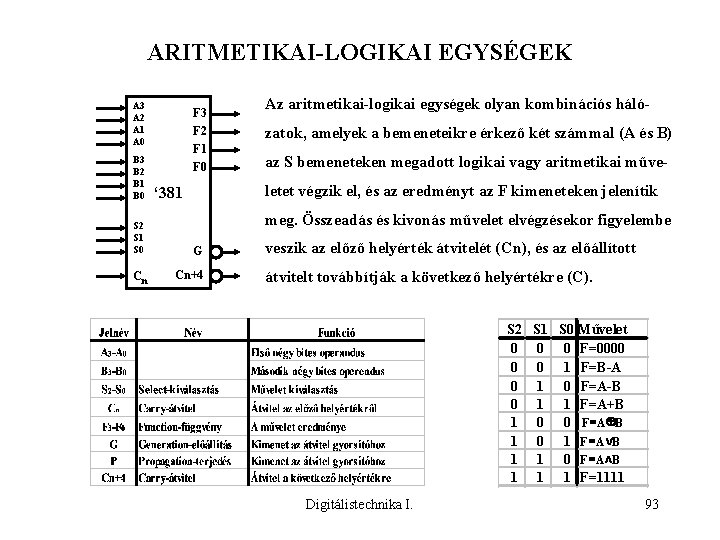
ARITMETIKAI-LOGIKAI EGYSÉGEK A 3 A 2 A 1 A 0 B 3 B 2 B 1 B 0 S 2 S 1 S 0 Cn F 3 Az aritmetikai-logikai egységek olyan kombinációs háló- F 2 zatok, amelyek a bemeneteikre érkező két számmal (A és B) F 1 F 0 az S bemeneteken megadott logikai vagy aritmetikai műveletet végzik el, és az eredményt az F kimeneteken jelenítik ‘ 381 meg. Összeadás és kivonás művelet elvégzésekor figyelembe G Cn+4 veszik az előző helyérték átvitelét (Cn), és az előállított átvitelt továbbítják a következő helyértékre (C). S 2 S 1 S 0 Művelet 0 0 0 F=0000 0 0 1 F=B-A 0 1 0 F=A-B 0 1 1 F=A+B 1 0 0 F =A ÅB 1 0 1 F =A ÚB 1 1 0 F =A ÙB 1 1 1 F=1111 Digitálistechnika I. 93

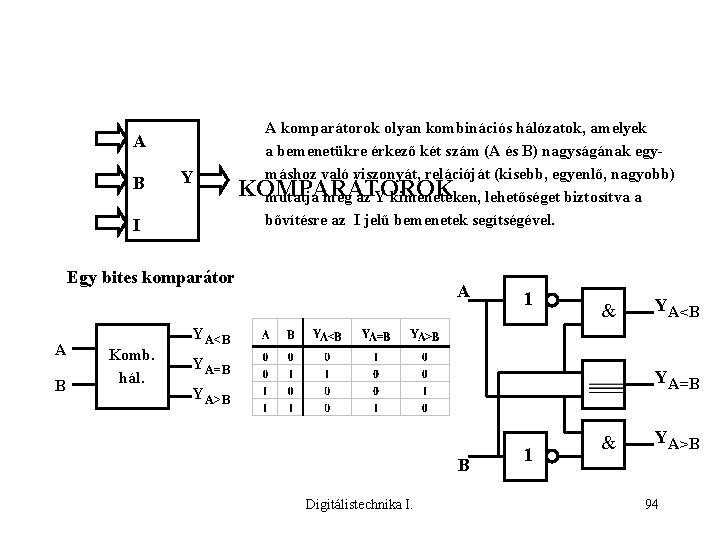
A B Y I A komparátorok olyan kombinációs hálózatok, amelyek a bemenetükre érkező két szám (A és B) nagyságának egymáshoz való viszonyát, relációját (kisebb, egyenlő, nagyobb) KOMPARÁTOROK mutatja meg az Y kimeneteken, lehetőséget biztosítva a bővítésre az I jelű bemenetek segítségével. Egy bites komparátor A B Komb. hál. A 1 & YA<B YA=B YA>B B Digitálistechnika I. 1 & YA>B 94

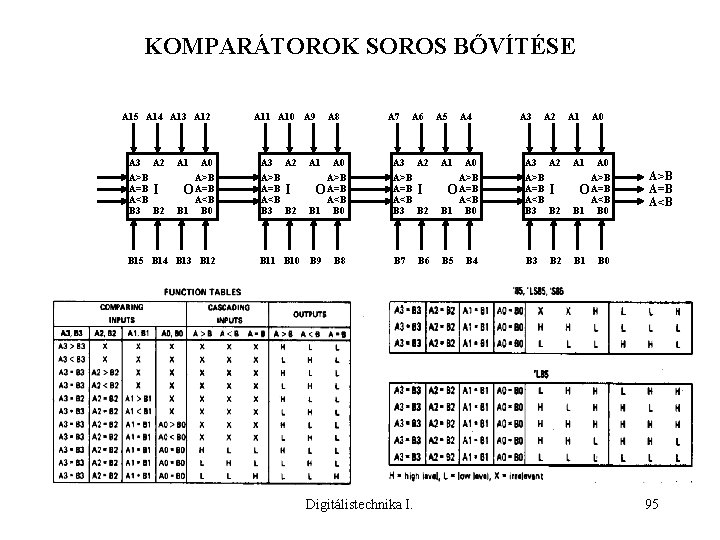
KOMPARÁTOROK SOROS BŐVÍTÉSE A 15 A 14 A 13 A 12 A 3 A 2 A>B A=B I A<B B 3 B 2 A 1 A 0 A>B O A=B A<B B 1 B 0 B 15 B 14 B 13 B 12 A 11 A 10 A 9 A 3 A 2 A>B A=B I A<B B 3 B 2 A 1 A 8 A 0 A>B O A=B A<B B 1 B 0 B 11 B 10 B 9 B 8 A 7 A 6 A 3 A 2 A 5 A 1 A 4 A 0 A 3 A 2 A 1 A 0 A>B A=B I A<B B 3 B 2 A>B O A=B A<B B 1 B 0 B 7 B 5 B 3 B 1 Digitálistechnika I. B 6 B 4 B 2 A>B A=B A<B B 0 95

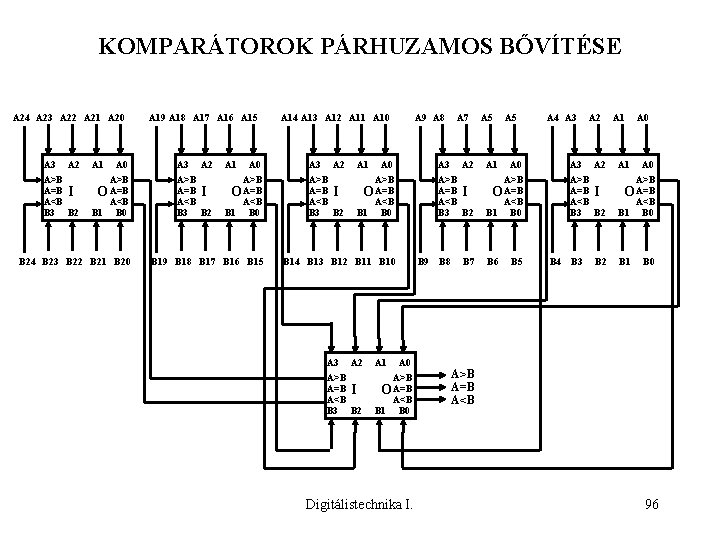
KOMPARÁTOROK PÁRHUZAMOS BŐVÍTÉSE A 24 A 23 A 22 A 21 A 20 A 3 A 2 A>B A=B I A<B B 3 B 2 A 1 A 0 A>B O A=B A<B B 1 B 0 B 24 B 23 B 22 B 21 B 20 A 19 A 18 A 17 A 16 A 15 A 3 A 2 A>B A=B I A<B B 3 B 2 A 1 A 0 A>B O A=B A<B B 1 B 0 B 19 B 18 B 17 B 16 B 15 A 14 A 13 A 12 A 11 A 10 A 3 A 2 A>B A=B I A<B B 3 B 2 A 1 A 9 A 8 A 0 A 3 A>B O A=B A<B B 1 B 0 A 2 A>B A=B I A<B B 3 B 2 A 1 A 2 A>B A=B I A<B B 3 B 2 B 14 B 13 B 12 B 11 B 10 A 3 A 7 B 9 B 8 A 0 A>B O A=B A<B B 1 B 0 Digitálistechnika I. B 7 A 5 A 1 A 5 A 0 A>B O A=B A<B B 1 B 0 B 6 B 5 A 4 A 3 A 2 A>B A=B I A<B B 3 B 2 B 4 B 3 B 2 A 1 A 0 A>B O A=B A<B B 1 B 0 A>B A=B A<B 96

12. ELŐADÁS TÁROLÓK • • SZEKVENCIÁLIS HÁLÓZATOK RS TÁROLÓK JK TÁROLÓK T ÉS D TÍPUSÚ TÁROLÓK Digitálistechnika I. 97

• SZEKVENCIÁLIS HÁLÓZATOK FOGALMA • SZEKVENCIÁLIS A TÁROLÓK HÁLÓZATOK – ALAPTÍPUSOK – FIZIKAI VEZÉRLÉS • SZÁMLÁLÓK – SZINRON SZÁMLÁLÓK – ASZINKRON SZÁMLÁLÓK • REGISZTEREK Digitálistechnika I. 98

SZEKVENCIÁLIS HÁLÓZATOK FOGALMA Belső állapot függvények X 1 X 2 Xn SORRENDI hálózat SH Q 1, Q 2, …Qp Z 1 Z 2 Zm Kimeneti függvények Digitálistechnika I. 99

TÁROLÓK • ÜZEMMÓDJAIK: • beírás • törlés • tárolás SET RESET STORE a tárolóba logikai „ 1” beírása a tárolóba logikai „ 0” beírása az előző állapot (0 vagy 1) megtartása • TÍPUSAIK: • • R-S tároló J-K tároló D tároló T tároló • VEZÉRLÉSI TÍPUSOK: • sztatikus tárolók • kapuzott tárolók • közbenső tárolású tárolók • élekkel vezérelt tárolók • élvezérlésű tárolók • vegyes vezérlésű tárolók Digitálistechnika I. 100

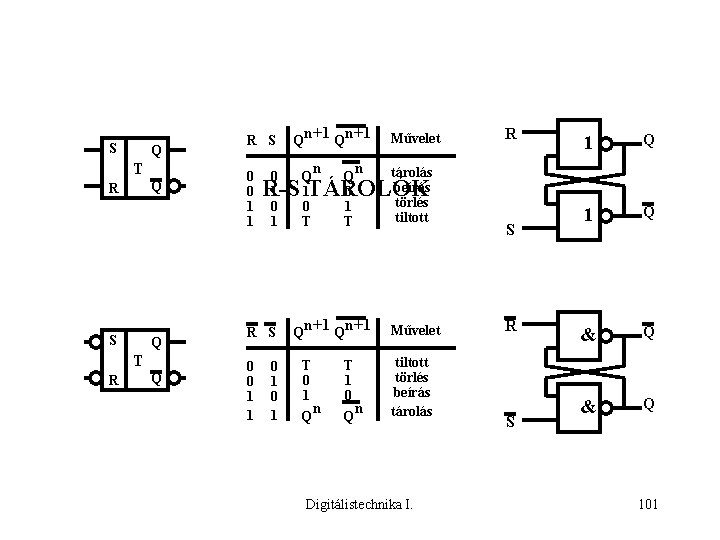
S Q T Q R S Q T R Q R S 0 0 1 1 0 1 n+1 Q 1 0 T n Q 0 1 T n Művelet tárolás beírás törlés tiltott R 1 Q & Q R-S TÁROLÓK R S 0 0 1 1 Q 0 1 n+1 Qn+1 Művelet T 0 1 n Q tiltott törlés beírás tárolás Q T 1 0 n Q Digitálistechnika I. S R S 101

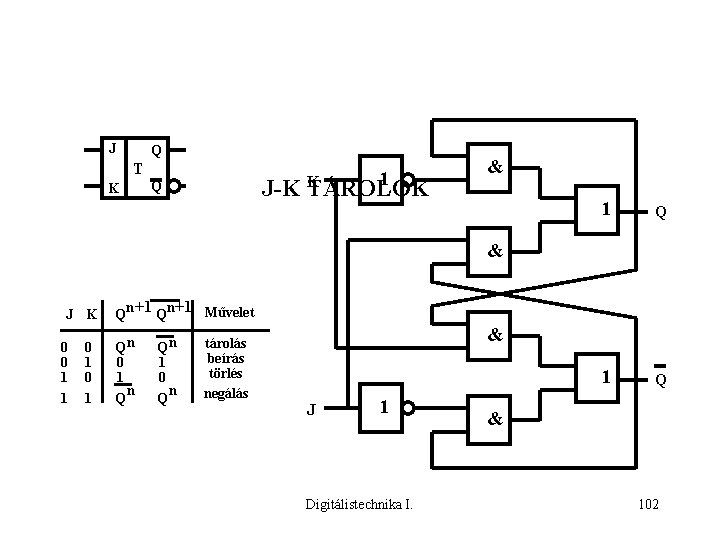
J Q T K J-K TÁROLÓK Q K 1 & 1 Q & J 0 0 1 1 n+1 Qn+1 Művelet K Q 0 1 Qn 0 1 n Q Qn 1 0 n Q tárolás beírás törlés negálás & J 1 Digitálistechnika I. & 102

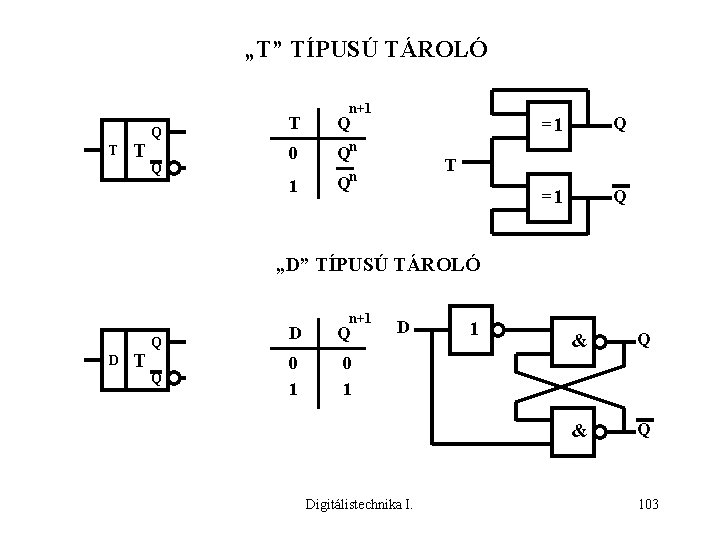
„T” TÍPUSÚ TÁROLÓ T T Q Q n+1 T Q 0 Qn 1 Qn =1 Q T „D” TÍPUSÚ TÁROLÓ D T Q Q n+1 D Q 0 1 D Digitálistechnika I. 1 & Q 103

13. ELŐADÁS TÁROLÓK VEZÉRLÉSE • KAPUZOTT TÁROLÓK • KÖZBENSŐ TÁROLÁSÚ TÁROLÓK • VEGYES VEZÉRLÉSŰ TÁROLÓK Digitálistechnika I. 104

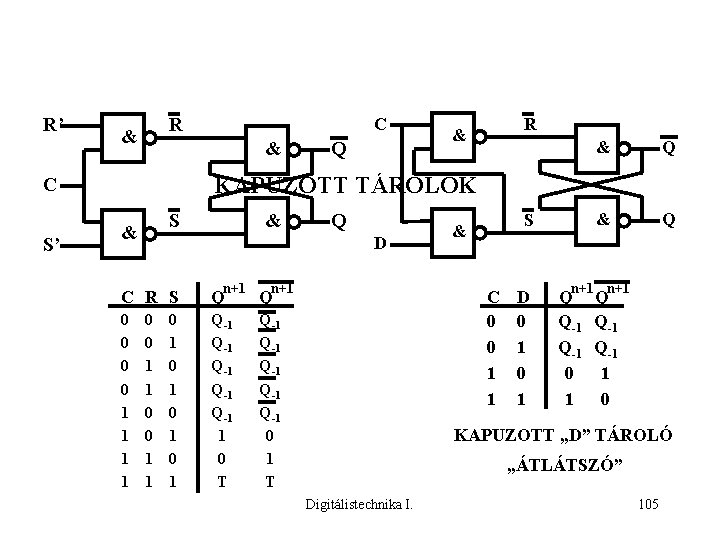
R’ R & & Q & Q KAPUZOTT TÁROLÓK C S’ C S & & Q D n+1 C R S Q Q 0 0 1 1 Q-1 Q-1 Q-1 1 0 T Q-1 Q-1 Q-1 0 1 T 0 0 1 1 0 1 0 1 S & C 0 0 1 1 D 0 1 n+1 Q Q Q-1 Q-1 0 1 1 0 KAPUZOTT „D” TÁROLÓ „ÁTLÁTSZÓ” Digitálistechnika I. 105

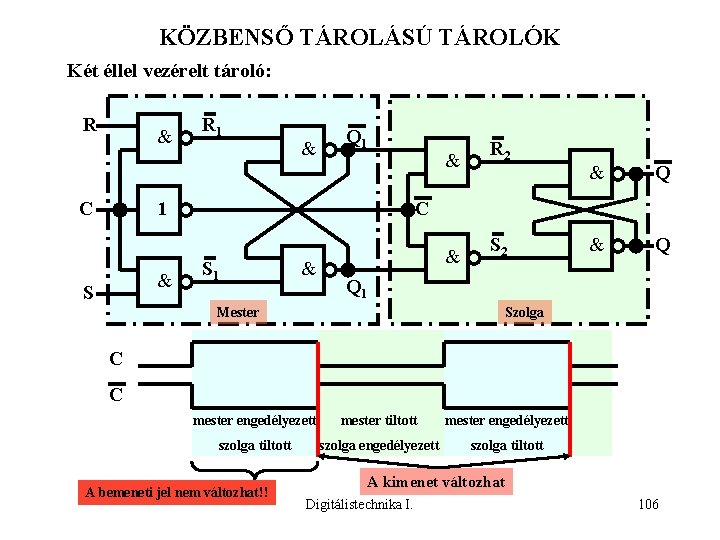
KÖZBENSŐ TÁROLÁSÚ TÁROLÓK Két éllel vezérelt tároló: R & C R 1 & Q 1 1 & S & R 2 & S 2 & Q C S 1 & Q 1 Mester Szolga C C mester engedélyezett mester tiltott mester engedélyezett szolga tiltott szolga engedélyezett szolga tiltott A bemeneti jel nem változhat!! A kimenet változhat Digitálistechnika I. 106

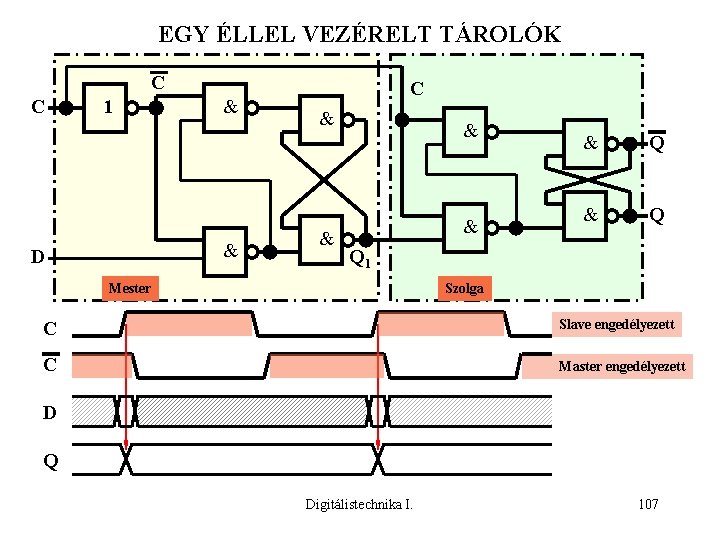
EGY ÉLLEL VEZÉRELT TÁROLÓK C C 1 & & D C & & & Q Q 1 Mester Szolga C Slave engedélyezett C Master engedélyezett D Q Digitálistechnika I. 107

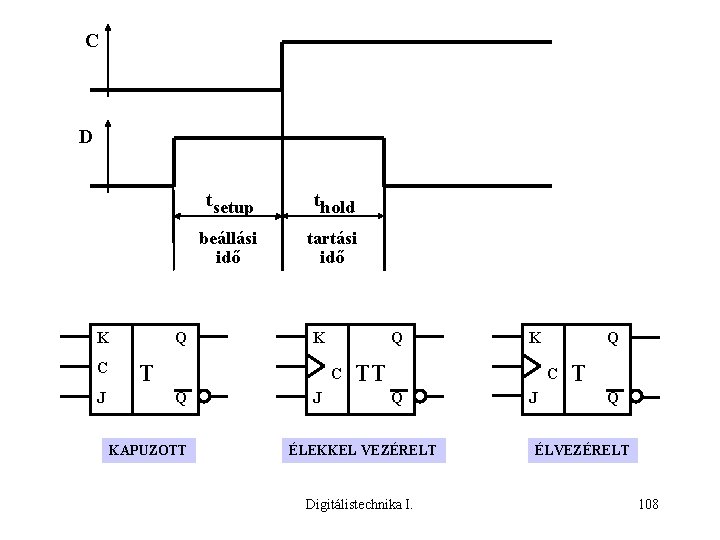
C D K C J Q tsetup thold beállási idő tartási idő K T Q C Q KAPUZOTT J K TT Q C Q ÉLEKKEL VEZÉRELT Digitálistechnika I. J T Q ÉLVEZÉRELT 108

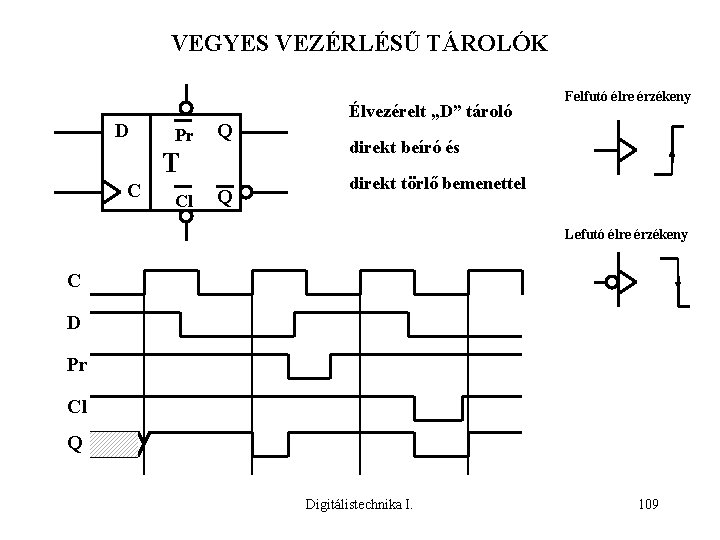
VEGYES VEZÉRLÉSŰ TÁROLÓK D Pr Q T C Cl Q Élvezérelt „D” tároló Felfutó élre érzékeny direkt beíró és direkt törlő bemenettel Lefutó élre érzékeny C D Pr Cl Q Digitálistechnika I. 109

14. ELŐADÁS REGISZTEREK • • • REGISZTEREK OSTÁLYOZÁSA PUFFER REGISZTER SHIFT REGISZTEREK FELHASZNÁLÁSA GYŰRŰS SZÁMLÁLÓK Digitálistechnika I. 110

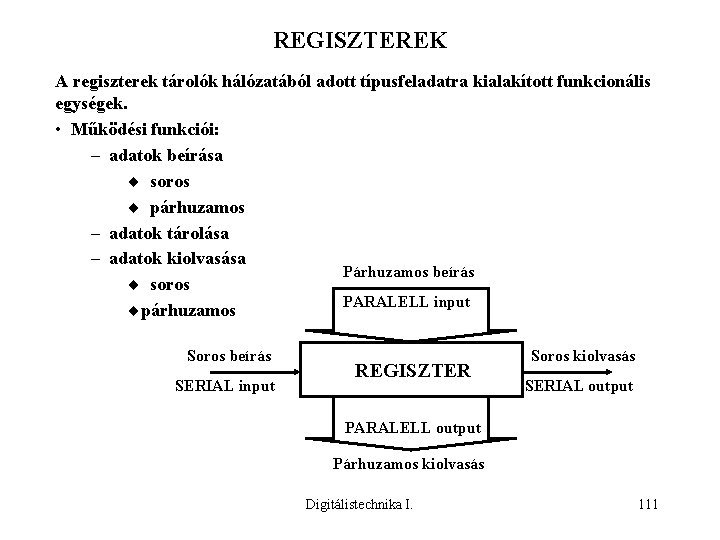
REGISZTEREK A regiszterek tárolók hálózatából adott típusfeladatra kialakított funkcionális egységek. • Működési funkciói: – adatok beírása ¨ soros ¨ párhuzamos – adatok tárolása – adatok kiolvasása Párhuzamos beírás ¨ soros PARALELL input ¨párhuzamos Soros beírás SERIAL input REGISZTER Soros kiolvasás SERIAL output PARALELL output Párhuzamos kiolvasás Digitálistechnika I. 111

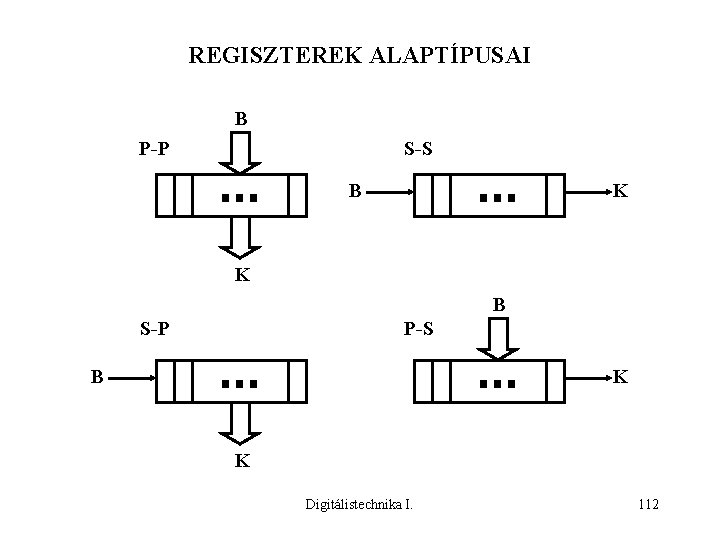
REGISZTEREK ALAPTÍPUSAI B P-P S-S B K K B S-P P-S B K K Digitálistechnika I. 112

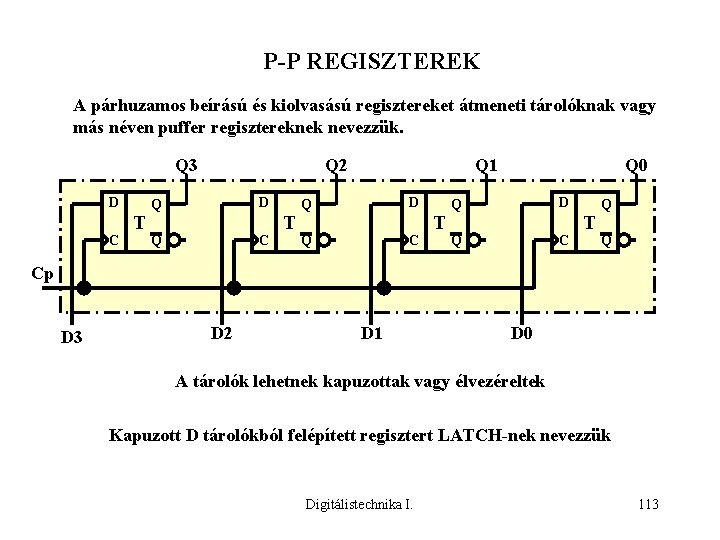
P-P REGISZTEREK A párhuzamos beírású és kiolvasású regisztereket átmeneti tárolóknak vagy más néven puffer regisztereknek nevezzük. Q 3 D C T Q 2 Q D Q C T Q 1 Q D Q C T Q 0 Q D Q C T Q Q Cp D 3 D 2 D 1 D 0 A tárolók lehetnek kapuzottak vagy élvezéreltek Kapuzott D tárolókból felépített regisztert LATCH-nek nevezzük Digitálistechnika I. 113

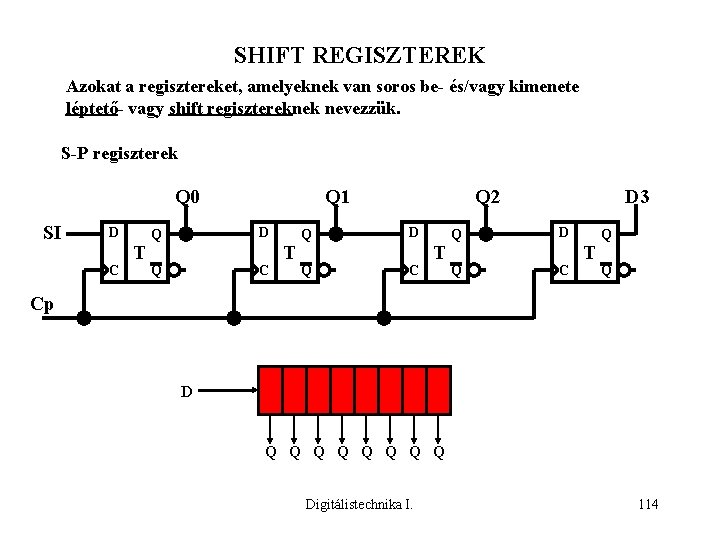
SHIFT REGISZTEREK Azokat a regisztereket, amelyeknek van soros be- és/vagy kimenete léptető- vagy shift regisztereknek nevezzük. S-P regiszterek Q 0 SI D C T Q 1 Q D Q C T Q 2 Q D Q C T D 3 Q D Q C T Q Q Cp D Q Q Q Q Digitálistechnika I. 114

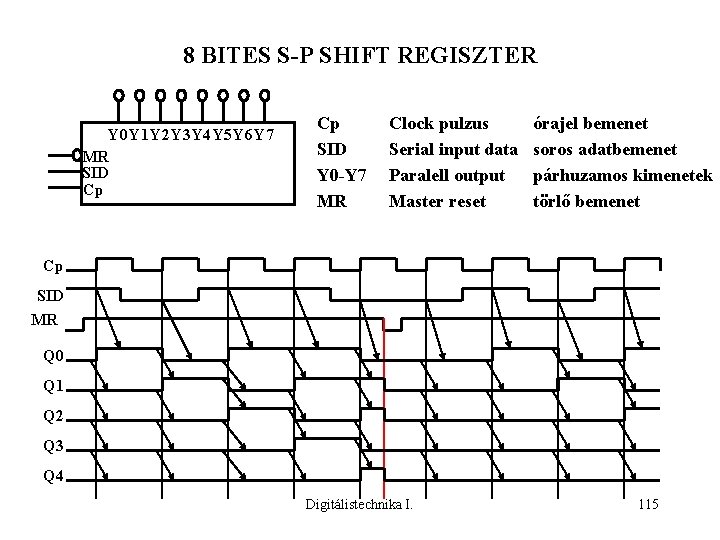
8 BITES S-P SHIFT REGISZTER Y 0 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7 MR SID Cp Cp SID Y 0 -Y 7 MR Clock pulzus Serial input data Paralell output Master reset órajel bemenet soros adatbemenet párhuzamos kimenetek törlő bemenet Cp SID MR Q 0 Q 1 Q 2 Q 3 Q 4 Digitálistechnika I. 115

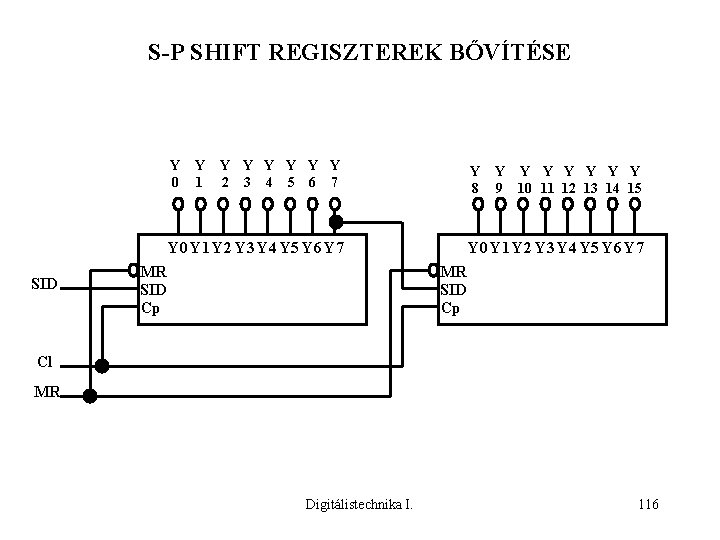
S-P SHIFT REGISZTEREK BŐVÍTÉSE Y 0 Y 1 Y Y Y 2 3 4 5 6 7 Y 8 Y 0 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7 SID Y Y Y Y 9 10 11 12 13 14 15 MR SID Cp Cl MR Digitálistechnika I. 116

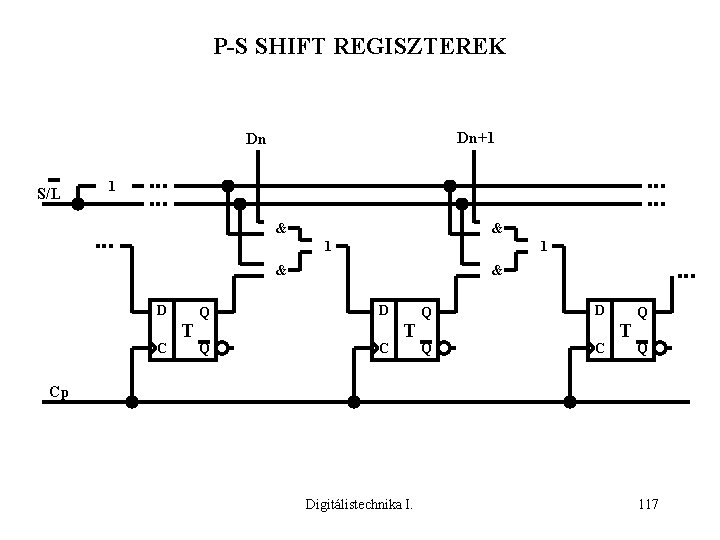
P-S SHIFT REGISZTEREK Dn+1 Dn S/L 1 & & 1 1 & D C T & Q D Q C T Q Q Cp Digitálistechnika I. 117

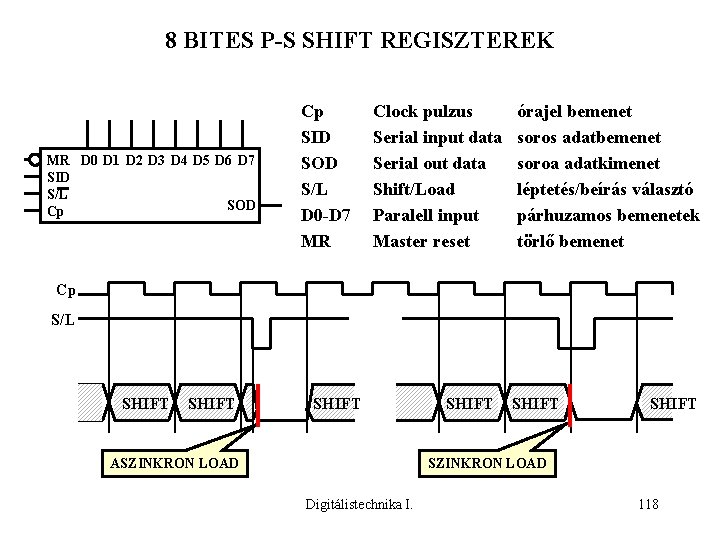
8 BITES P-S SHIFT REGISZTEREK MR D 0 D 1 D 2 D 3 D 4 D 5 D 6 D 7 SID S/L SOD Cp Cp SID SOD S/L D 0 -D 7 MR Clock pulzus Serial input data Serial out data Shift/Load Paralell input Master reset órajel bemenet soros adatbemenet soroa adatkimenet léptetés/beírás választó párhuzamos bemenetek törlő bemenet Cp S/L SHIFT ASZINKRON LOAD SHIFT SZINKRON LOAD Digitálistechnika I. 118

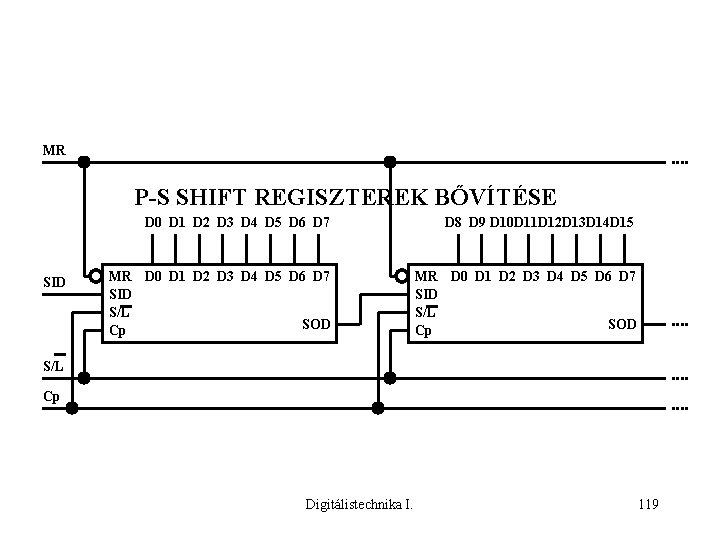
MR P-S SHIFT REGISZTEREK BŐVÍTÉSE SID D 0 D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 D 10 D 11 D 12 D 13 D 14 D 15 MR D 0 D 1 D 2 D 3 D 4 D 5 D 6 D 7 SID S/L SOD Cp S/L Cp Digitálistechnika I. 119

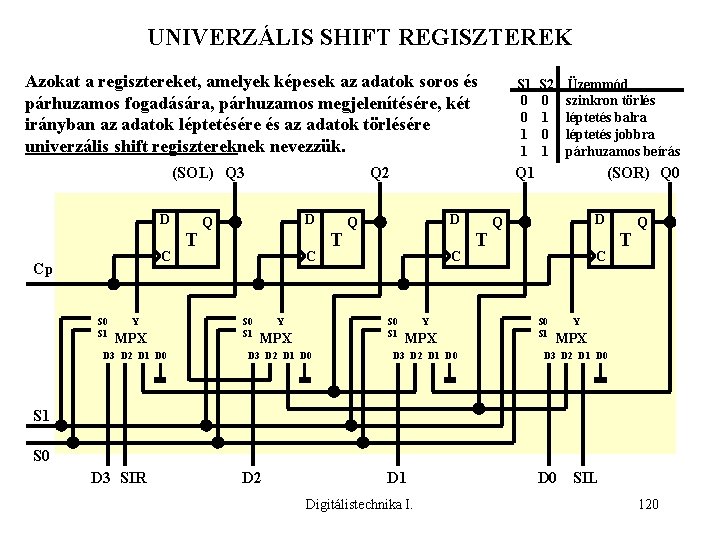
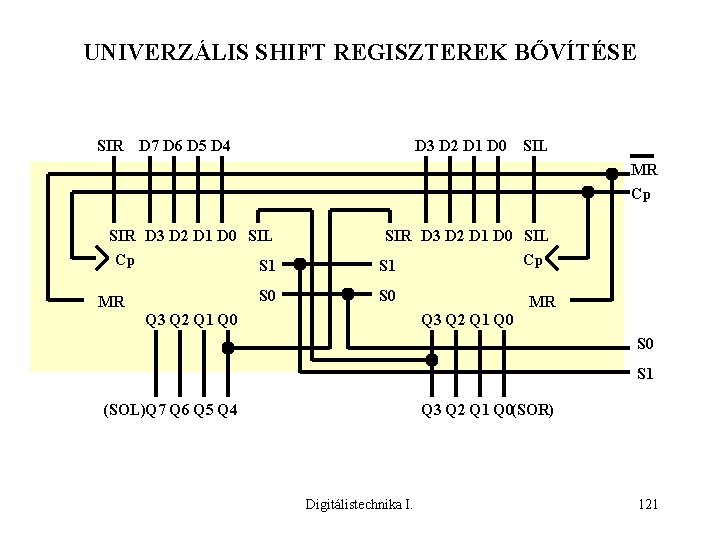
UNIVERZÁLIS SHIFT REGISZTEREK Azokat a regisztereket, amelyek képesek az adatok soros és párhuzamos fogadására, párhuzamos megjelenítésére, két irányban az adatok léptetésére és az adatok törlésére univerzális shift regisztereknek nevezzük. (SOL) Q 3 D C Cp S 0 S 1 Y MPX D 3 D 2 D 1 D 0 T S 1 0 0 1 1 Q 2 D Q C S 0 S 1 Y T D 3 D 2 D 1 D 0 Üzemmód szinkron törlés léptetés balra léptetés jobbra párhuzamos beírás Q 1 D Q C S 0 S 1 MPX S 2 0 1 Y MPX D 3 D 2 D 1 D 0 T (SOR) Q 0 D Q C S 0 S 1 T Q Y MPX D 3 D 2 D 1 D 0 S 1 S 0 D 3 SIR D 2 D 1 Digitálistechnika I. D 0 SIL 120

UNIVERZÁLIS SHIFT REGISZTEREK BŐVÍTÉSE SIR D 7 D 6 D 5 D 4 D 3 D 2 D 1 D 0 SIL MR Cp SIR D 3 D 2 D 1 D 0 SIL Cp S 1 S 0 MR SIR D 3 D 2 D 1 D 0 SIL Cp S 1 S 0 Q 3 Q 2 Q 1 Q 0 MR Q 3 Q 2 Q 1 Q 0 S 1 (SOL)Q 7 Q 6 Q 5 Q 4 Q 3 Q 2 Q 1 Q 0(SOR) Digitálistechnika I. 121

• PUFFER REGISZTEREK ADATOK ÁTMENETI TÁROLÁSA REGISZTEREK FELHASZNÁLÁSA • SHIFT REGISZTEREK FORMÁTUM ÁTALAKÍTÁS • S-P SOROS / PÁRHUZAMOS ÁTALAKÍTÁS • P-S PÁRHUZAMOS / SOROS ÁTALAKÍTÁS GYŰRŰS SZÁMLÁLÓK • N-BŐL 1 SZÁMLÁLÓ • JOHNSON SZÁMLÁLÓ • MAXIMÁLIS HOSSZÚSÁGÚ SZÁMLÁLÓ Digitálistechnika I. 122

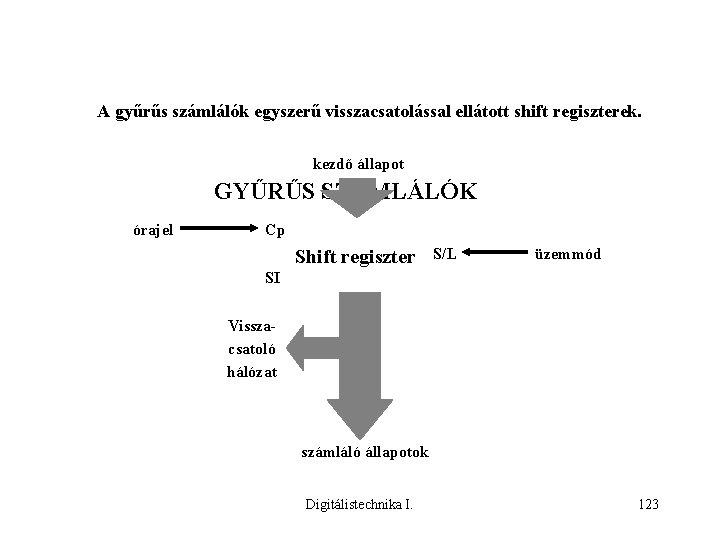
A gyűrűs számlálók egyszerű visszacsatolással ellátott shift regiszterek. kezdő állapot GYŰRŰS SZÁMLÁLÓK órajel Cp Shift regiszter S/L üzemmód SI Visszacsatoló hálózat számláló állapotok Digitálistechnika I. 123

„ 1”„ 0”„ 0” D 3 N-BŐL D 2 D 1 D 0 órajel 1 SZÁMLÁLÓ Cp S/L SI Alaphelyzetbe állítás Q 3 Q 2 Q 1 Q 0 Q 3 1 0 0 0 1 Digitálistechnika I. Q 2 0 1 0 0 0 Q 1 0 0 Q 0 0 1 0 Órajel ciklus alaphelyzet 1. órajel 2. órajel 3. órajel 4. órajel 124

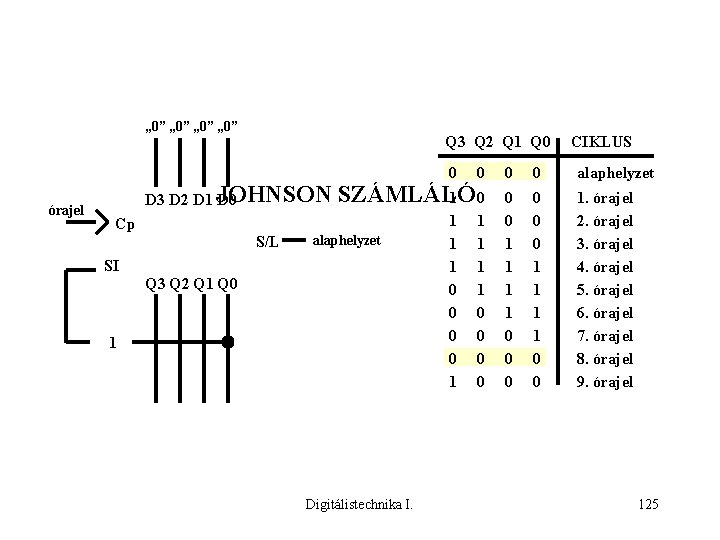
„ 0” órajel Q 3 Q 2 Q 1 Q 0 D 3 D 2 D 1 JOHNSON D 0 0 alaphelyzet 1 1 1 1 0 0 0 1 1 0 0 1. órajel 2. órajel 3. órajel 4. órajel 5. órajel 6. órajel 7. órajel 8. órajel 9. órajel SZÁMLÁLÓ 1 0 Cp S/L 0 alaphelyzet SI Q 3 Q 2 Q 1 Q 0 1 Digitálistechnika I. 1 1 1 0 0 1 CIKLUS 125

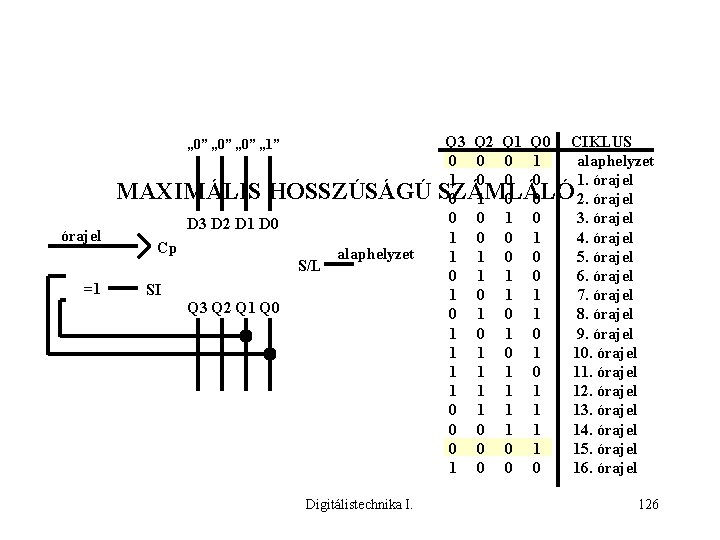
„ 0” „ 1” MAXIMÁLIS HOSSZÚSÁGÚ órajel D 3 D 2 D 1 D 0 Cp S/L =1 alaphelyzet SI Q 3 Q 2 Q 1 Q 0 Digitálistechnika I. Q 3 Q 2 Q 1 Q 0 CIKLUS 0 0 0 1 alaphelyzet 1 0 0 0 1. órajel SZÁMLÁLÓ 0 1 0 0 2. órajel 0 0 1 0 3. órajel 1 0 0 1 4. órajel 1 1 0 0 5. órajel 0 1 1 0 6. órajel 1 0 1 1 7. órajel 0 1 8. órajel 1 0 9. órajel 1 1 0 1 10. órajel 1 1 1 0 11. órajel 1 1 12. órajel 0 1 13. órajel 0 0 1 1 14. órajel 0 0 0 1 15. órajel 1 0 0 0 16. órajel 126

15. ELŐADÁS SZÁMLÁLÓK • • • ASZINKRON SZÁMLÁLÓK REVERZIBILIS SZÁMLÁLÓK SZOLGÁLTATÁSAI (Cl; Ld) CIKLUSRÖVIDÍTÉS Digitálistechnika I. 127

SZÁMLÁLÓK A számlálók olyan szekvenciális áramkörök, amelyek a Cp bemenetükre érkező impulzusokat összeszámlálják, és az eredményt a Q kimeneteken jelenítik meg. ¨ Vezérlési mód szempontjából: • aszinkron • szinkron ¨ Számlálás kódja szerint: • bináris • BCD ¨ Számlálás iránya szerint: • előre számlálók • reverzibilis számlálók ¨ Egyéb szolgáltatások: • szinkron/aszinkron törlés • szinkron aszinkron kezdőérték beállítás (programozhatóság) Digitálistechnika I. 128

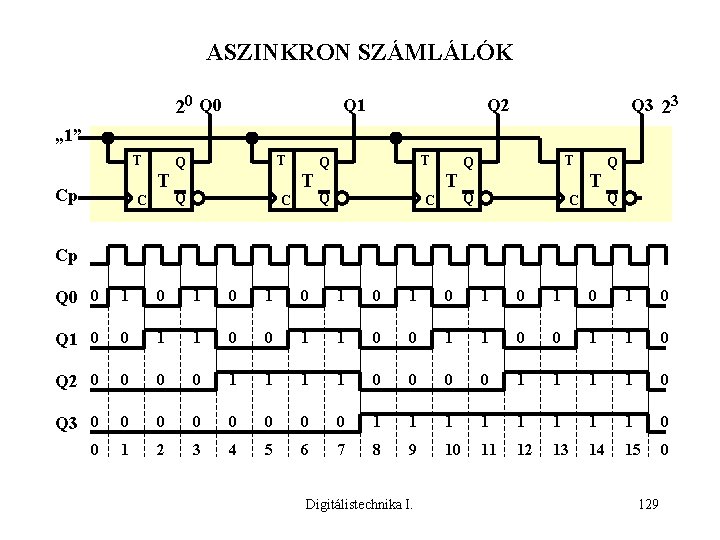
ASZINKRON SZÁMLÁLÓK 20 Q 1 Q 3 23 Q 2 „ 1” T T Cp C Q T Q C T Q Q Cp Q 0 0 1 0 1 0 Q 1 0 0 1 1 0 Q 2 0 0 0 0 1 1 1 1 0 Q 3 0 0 0 0 1 1 1 1 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 Digitálistechnika I. 129

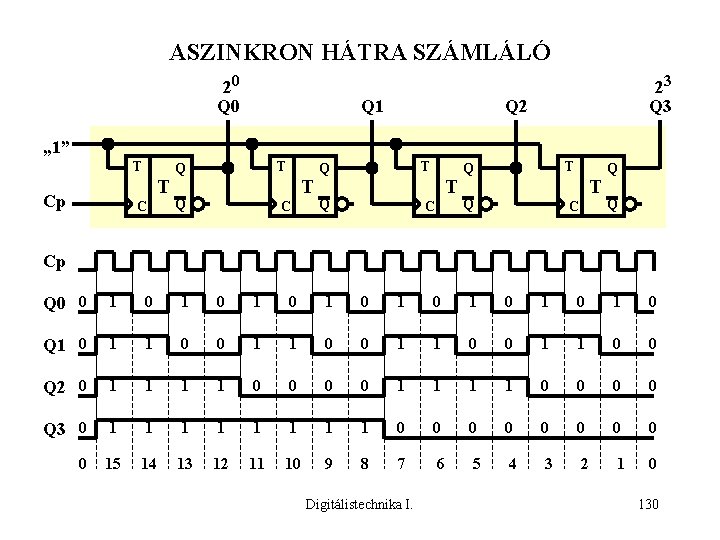
ASZINKRON HÁTRA SZÁMLÁLÓ 20 Q 1 23 Q 2 „ 1” T T Cp C Q T Q C T Q Q Cp Q 0 0 1 0 1 0 Q 1 0 1 1 0 0 Q 2 0 1 1 1 1 0 0 0 0 Q 3 0 1 1 1 1 0 0 0 0 0 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 Digitálistechnika I. 130

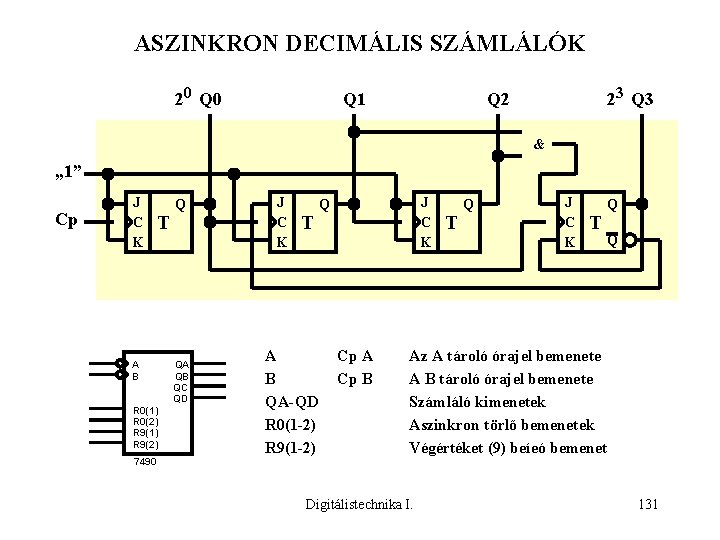
ASZINKRON DECIMÁLIS SZÁMLÁLÓK 20 Q 1 23 Q 2 & „ 1” Cp J C K T A B R 0(1) R 0(2) R 9(1) R 9(2) 7490 Q QA QB QC QD J C K T A B QA-QD R 0(1 -2) R 9(1 -2) J C K Q Cp A Cp B T Q J C K T Q Q Az A tároló órajel bemenete A B tároló órajel bemenete Számláló kimenetek Aszinkron törlő bemenetek Végértéket (9) beíeó bemenet Digitálistechnika I. 131

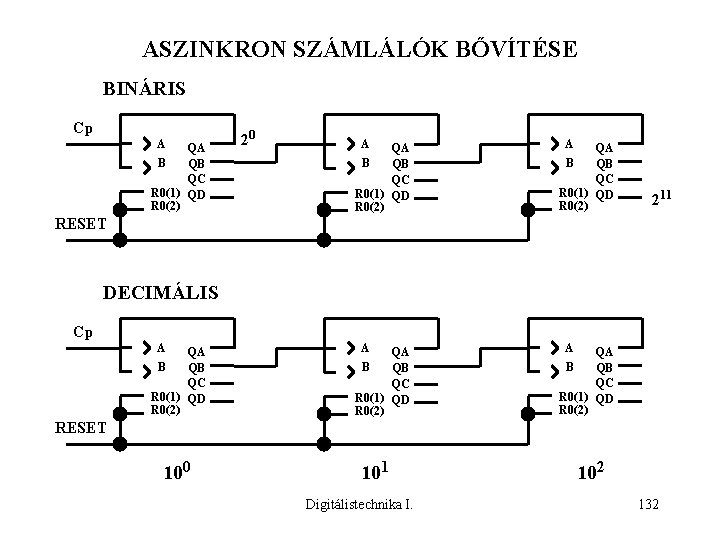
ASZINKRON SZÁMLÁLÓK BŐVÍTÉSE BINÁRIS Cp A QA B QB QC R 0(1) QD R 0(2) 20 A QA B QB QC R 0(1) QD R 0(2) 211 RESET DECIMÁLIS Cp A QA B QB QC R 0(1) QD R 0(2) RESET 100 101 Digitálistechnika I. 102 132

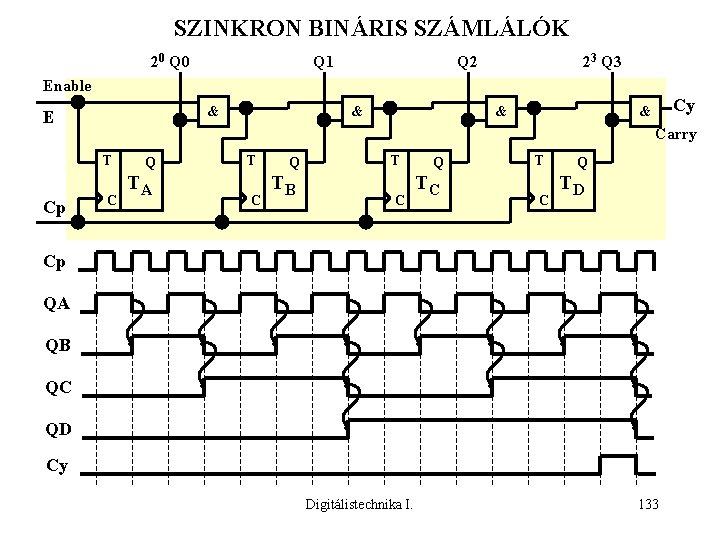
SZINKRON BINÁRIS SZÁMLÁLÓK 20 Q 1 23 Q 2 Enable & E & Cy & Carry T Cp & C Q TA T C Q TB T C Q TC T C Q TD Cp QA QB QC QD Cy Digitálistechnika I. 133

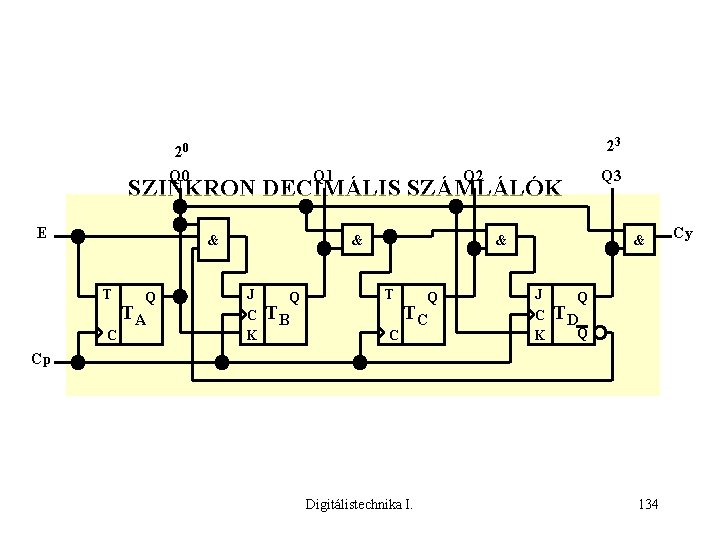
23 20 Q 1 Q 2 Q 3 SZINKRON DECIMÁLIS SZÁMLÁLÓK E & T C Q TA & J C K TB Q & T C Q TC & J C K Q TD Q Cp Digitálistechnika I. 134 Cy

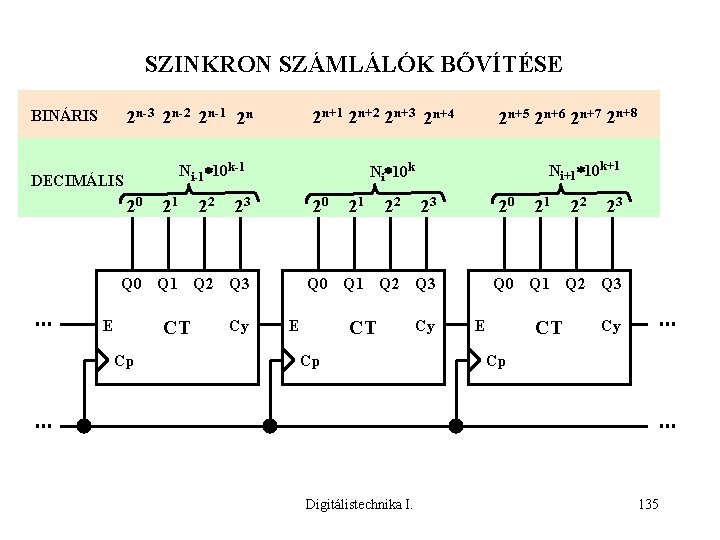
SZINKRON SZÁMLÁLÓK BŐVÍTÉSE 2 n-3 2 n-2 2 n-1 2 n BINÁRIS 2 n+1 2 n+2 2 n+3 2 n+4 Ni-1 10 k-1 DECIMÁLIS 20 21 22 CT 23 Cp Cy Ni+1 10 k+1 Ni 10 k 20 Q 1 Q 2 Q 3 E 2 n+5 2 n+6 2 n+7 2 n+8 21 22 23 20 Q 1 Q 2 Q 3 CT E Cp Digitálistechnika I. Cy 21 22 23 Q 0 Q 1 Q 2 Q 3 CT E Cy Cp 135

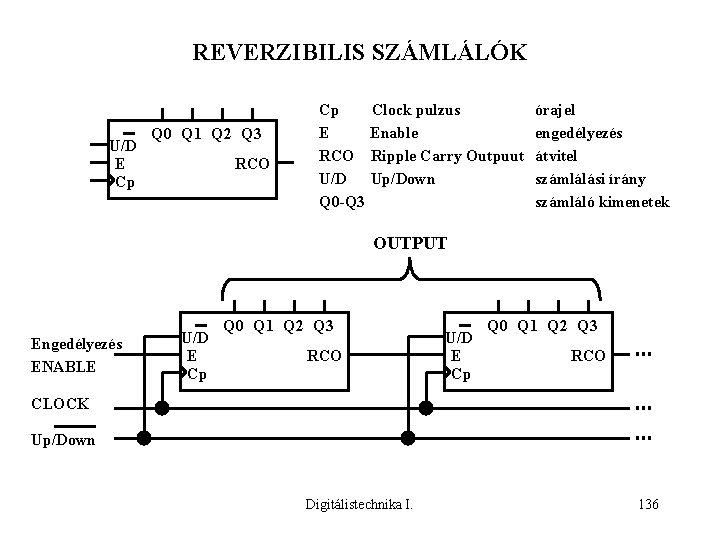
REVERZIBILIS SZÁMLÁLÓK U/D E Cp Q 0 Q 1 Q 2 Q 3 RCO Cp Clock pulzus E Enable RCO Ripple Carry Outpuut U/D Up/Down Q 0 -Q 3 órajel engedélyezés átvitel számlálási írány számláló kimenetek OUTPUT Engedélyezés ENABLE U/D E Cp Q 0 Q 1 Q 2 Q 3 RCO CLOCK Up/Down Digitálistechnika I. 136

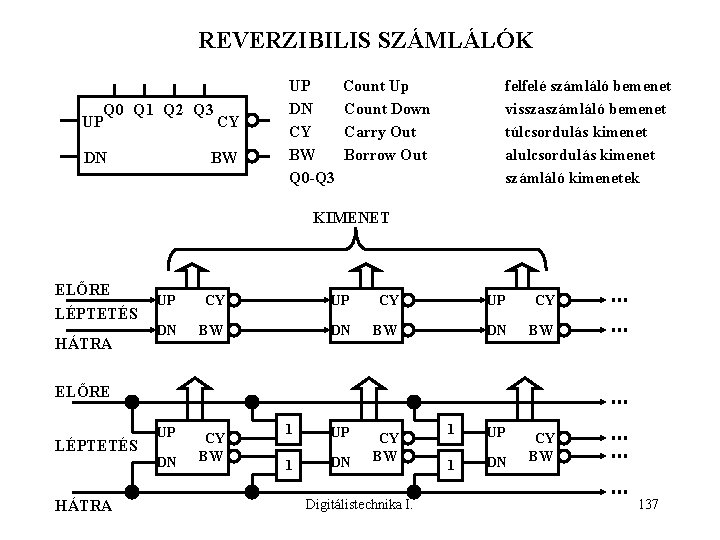
REVERZIBILIS SZÁMLÁLÓK Q 0 Q 1 Q 2 Q 3 UP CY DN BW UP DN CY BW Q 0 -Q 3 Count Up Count Down Carry Out Borrow Out felfelé számláló bemenet visszaszámláló bemenet túlcsordulás kimenet alulcsordulás kimenet számláló kimenetek KIMENET ELŐRE LÉPTETÉS HÁTRA UP CY DN BW UP CY BW 1 UP 1 DN CY BW ELŐRE LÉPTETÉS DN HÁTRA Digitálistechnika I. 137

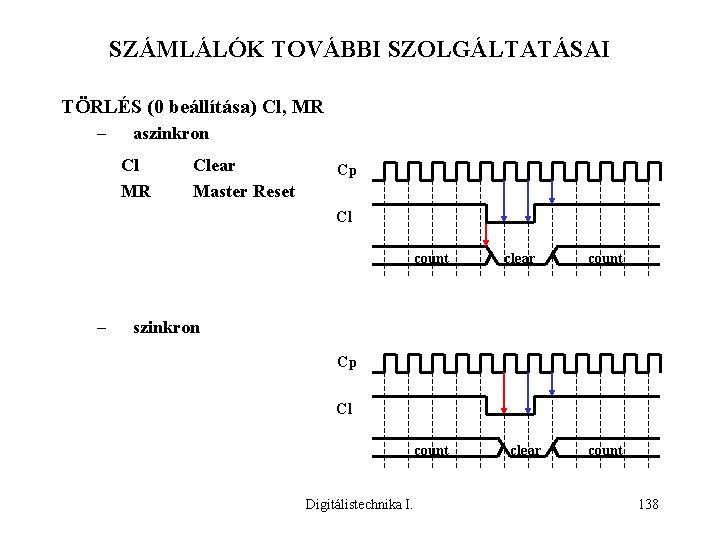
SZÁMLÁLÓK TOVÁBBI SZOLGÁLTATÁSAI TÖRLÉS (0 beállítása) Cl, MR – aszinkron Cl MR Clear Master Reset Cp Cl count – clear count szinkron Cp Cl count Digitálistechnika I. clear count 138

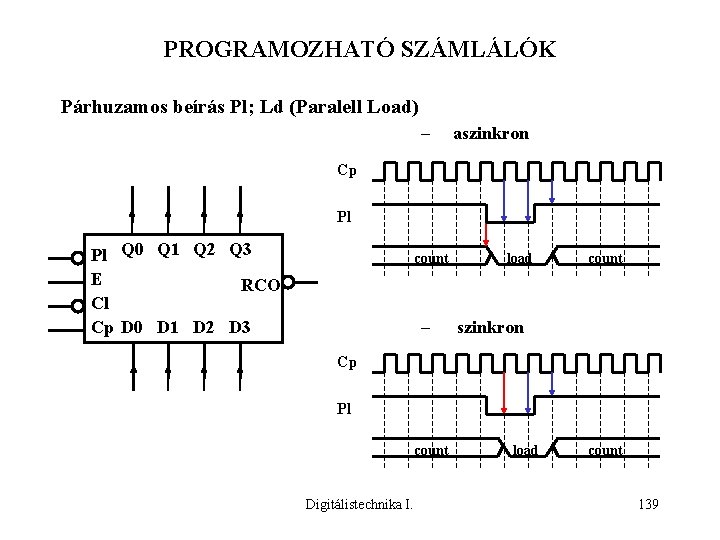
PROGRAMOZHATÓ SZÁMLÁLÓK Párhuzamos beírás Pl; Ld (Paralell Load) – aszinkron Cp Pl Pl Q 0 Q 1 Q 2 Q 3 E RCO Cl Cp D 0 D 1 D 2 D 3 count – load count szinkron Cp Pl count Digitálistechnika I. load count 139

SZÁMLÁLÓK CIKLUS RÖVIDÍTÉSE 4 bites számlálók ciklusai BINÁRIS: 0 1 2 3 4 5 6 7 8 9 A B C D E F DECIMÁLIS: 0 1 2 3 4 5 6 7 8 9 RÖVIDÍTETTCIKLUS: 0 1 2 3 4 5 6 7 8 9 A B C CILKUS RÖVIDÍTÉS: SZINKRON CLEAR ESTÉN ASZINKRON CLEAR ESETÉN Digitálistechnika I. 140

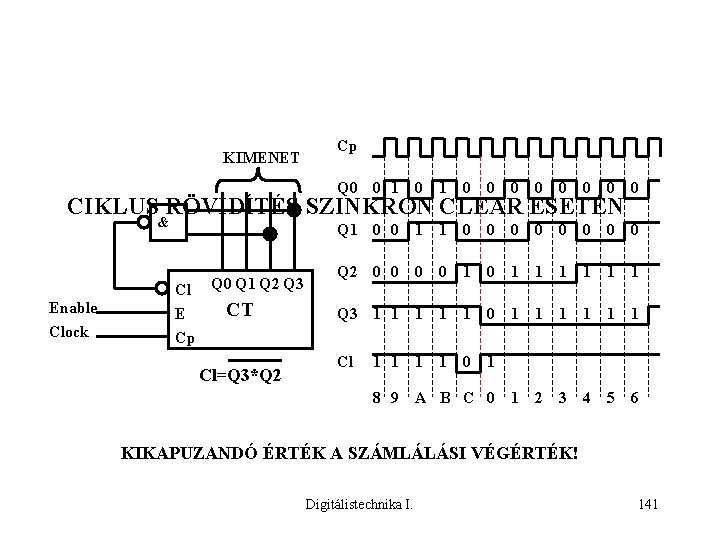
KIMENET Cp Q 0 0 1 0 0 0 0 Q 1 0 0 1 1 0 0 0 0 Q 2 0 0 1 0 1 1 1 Q 3 1 1 1 0 1 1 1 Cl 1 1 1 CIKLUS RÖVIDÍTÉS SZINKRON CLEAR ESETÉN & Enable Clock Cl E Cp Q 0 Q 1 Q 2 Q 3 CT Cl=Q 3*Q 2 1 1 0 8 9 A B C 0 1 2 3 4 5 6 KIKAPUZANDÓ ÉRTÉK A SZÁMLÁLÁSI VÉGÉRTÉK! Digitálistechnika I. 141

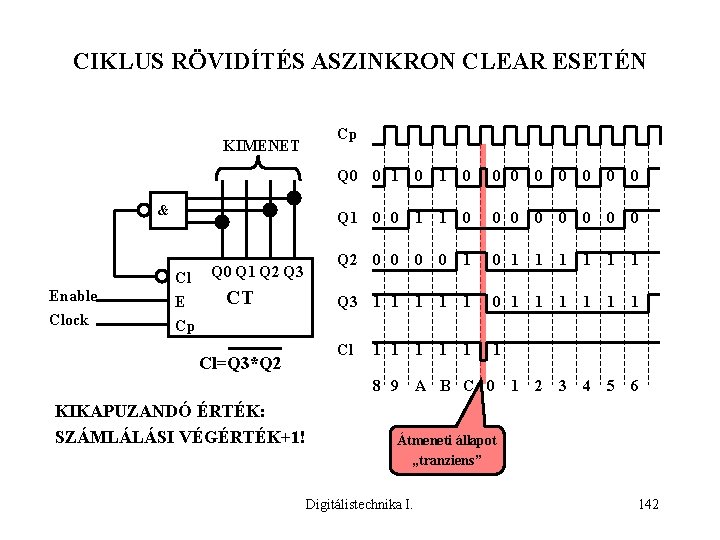
CIKLUS RÖVIDÍTÉS ASZINKRON CLEAR ESETÉN KIMENET & Enable Clock Cl E Cp Q 0 Q 1 Q 2 Q 3 CT Cl=Q 3*Q 2 Cp Q 0 0 1 0 0 0 0 Q 1 0 0 1 1 0 0 0 0 Q 2 0 0 1 0 1 1 1 Q 3 1 1 1 0 1 1 1 Cl 1 1 1 8 9 A B C 0 KIKAPUZANDÓ ÉRTÉK: SZÁMLÁLÁSI VÉGÉRTÉK+1! 1 2 3 4 5 6 Átmeneti állapot „tranziens” Digitálistechnika I. 142

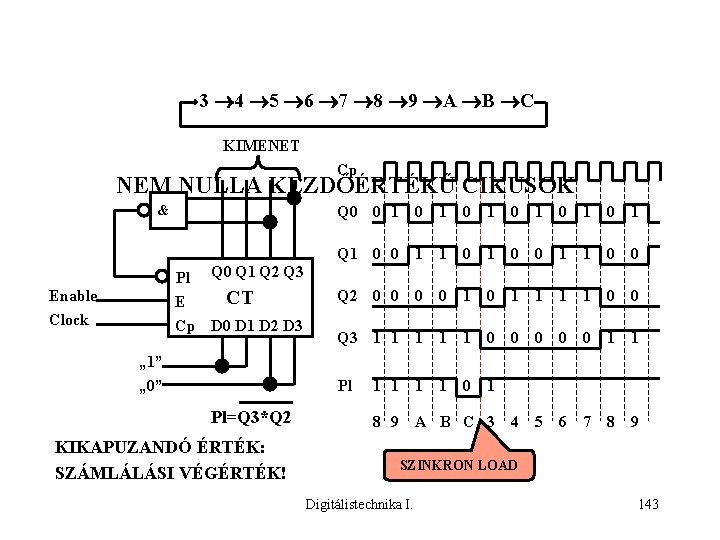
3 4 5 6 7 8 9 A B C KIMENET Cp NEM NULLA KEZDŐÉRTÉKŰ CIKUSOK & Pl Q 0 Q 1 Q 2 Q 3 CT E Cp D 0 D 1 D 2 D 3 Enable Clock „ 1” „ 0” Pl=Q 3*Q 2 KIKAPUZANDÓ ÉRTÉK: SZÁMLÁLÁSI VÉGÉRTÉK! Q 0 0 1 0 1 0 1 Q 1 0 0 1 1 0 0 Q 2 0 0 1 0 1 1 0 0 Q 3 1 1 1 0 0 0 1 1 Pl 1 1 1 0 8 9 A B C 3 4 5 6 7 8 9 SZINKRON LOAD Digitálistechnika I. 143

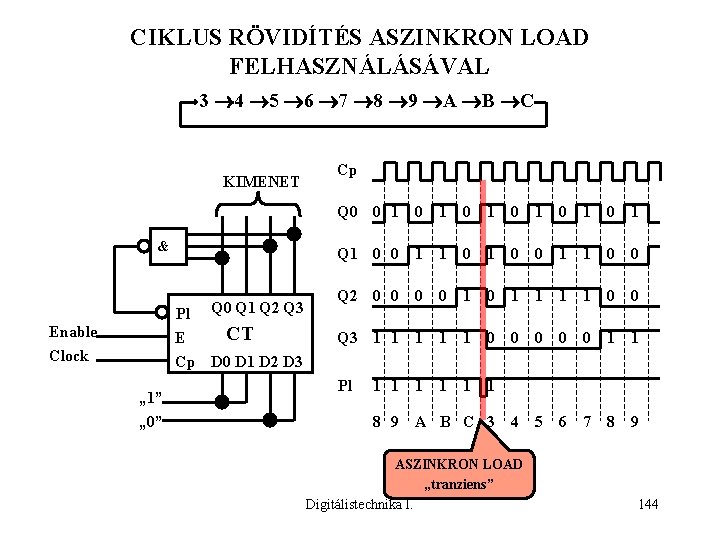
CIKLUS RÖVIDÍTÉS ASZINKRON LOAD FELHASZNÁLÁSÁVAL 3 4 5 6 7 8 9 A B C KIMENET & Q 0 Q 1 Q 2 Q 3 Pl CT E Cp D 0 D 1 D 2 D 3 Enable Clock „ 1” „ 0” Cp Q 0 0 1 0 1 0 1 Q 1 0 0 1 1 0 0 Q 2 0 0 1 0 1 1 0 0 Q 3 1 1 1 0 0 0 1 1 Pl 1 1 1 8 9 A B C 3 4 ASZINKRON LOAD „tranziens” Digitálistechnika I. 5 6 7 8 9 144