Digitalni sistemi Sekvenna preklopna vezja 7 Sekvenna preklopna

Digitalni sistemi Sekvenčna preklopna vezja 7 Sekvenčna preklopna vezja Digitalni sistemi dr. Bogdan Dugonik Univerza v Mariboru Tehniška fakulteta Elektrotehnika, računalništvo in informatika (delovna verzija) Prosojnica št. 7 -1

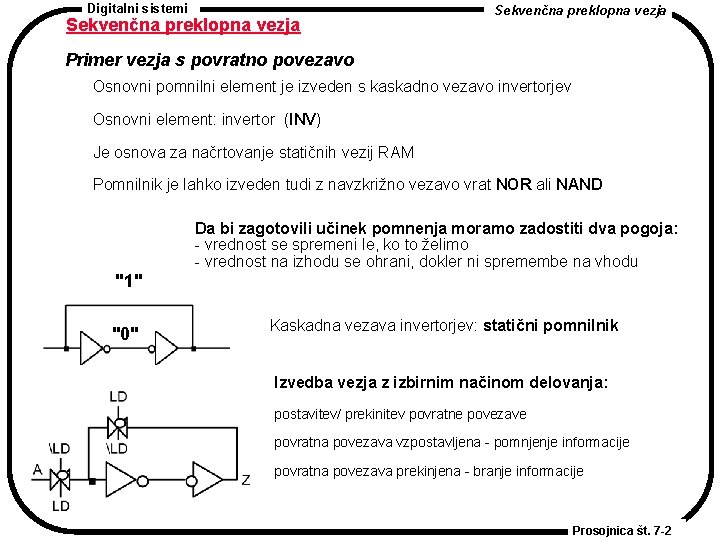
Digitalni sistemi Sekvenčna preklopna vezja Primer vezja s povratno povezavo Osnovni pomnilni element je izveden s kaskadno vezavo invertorjev Osnovni element: invertor (INV) Je osnova za načrtovanje statičnih vezij RAM Pomnilnik je lahko izveden tudi z navzkrižno vezavo vrat NOR ali NAND Da bi zagotovili učinek pomnenja moramo zadostiti dva pogoja: - vrednost se spremeni le, ko to želimo - vrednost na izhodu se ohrani, dokler ni spremembe na vhodu "1" "0" Kaskadna vezava invertorjev: statični pomnilnik Izvedba vezja z izbirnim načinom delovanja: postavitev/ prekinitev povratne povezave povratna povezava vzpostavljena - pomnjenje informacije povratna povezava prekinjena - branje informacije Prosojnica št. 7 -2

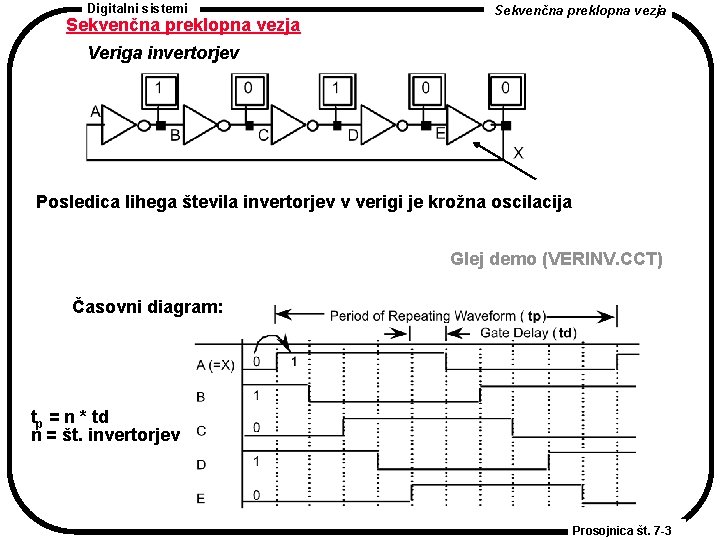
Digitalni sistemi Sekvenčna preklopna vezja Veriga invertorjev Posledica lihega števila invertorjev v verigi je krožna oscilacija Glej demo (VERINV. CCT) Časovni diagram: tp = n * td n = št. invertorjev Prosojnica št. 7 -3

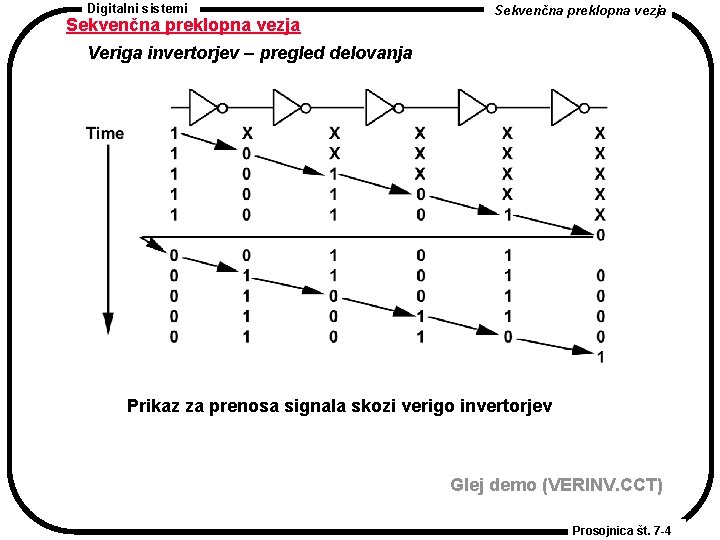
Digitalni sistemi Sekvenčna preklopna vezja Veriga invertorjev – pregled delovanja Prikaz za prenosa signala skozi verigo invertorjev Glej demo (VERINV. CCT) Prosojnica št. 7 -4

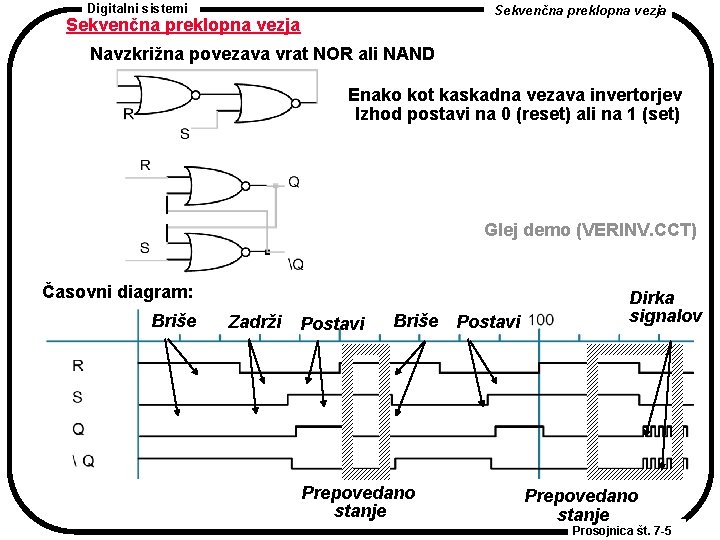
Digitalni sistemi Sekvenčna preklopna vezja Navzkrižna povezava vrat NOR ali NAND Enako kot kaskadna vezava invertorjev Izhod postavi na 0 (reset) ali na 1 (set) Glej demo (VERINV. CCT) Časovni diagram: Briše Zadrži Postavi Briše Postavi Prepovedano stanje Dirka signalov Prepovedano stanje Prosojnica št. 7 -5

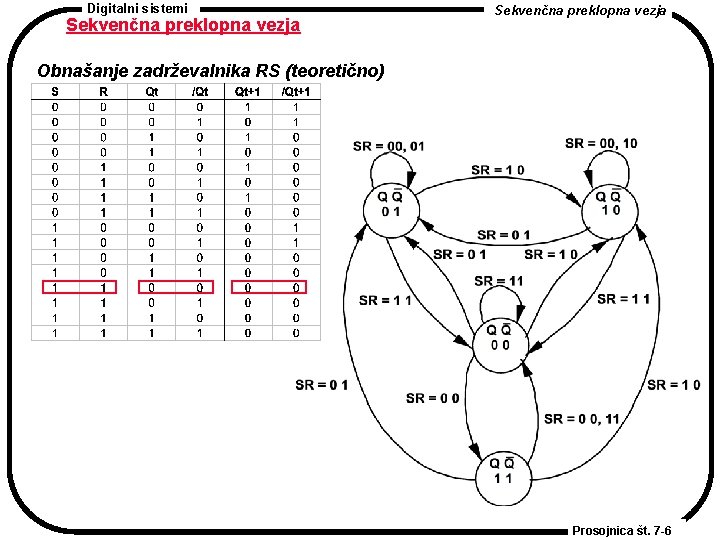
Digitalni sistemi Sekvenčna preklopna vezja Obnašanje zadrževalnika RS (teoretično) Prosojnica št. 7 -6

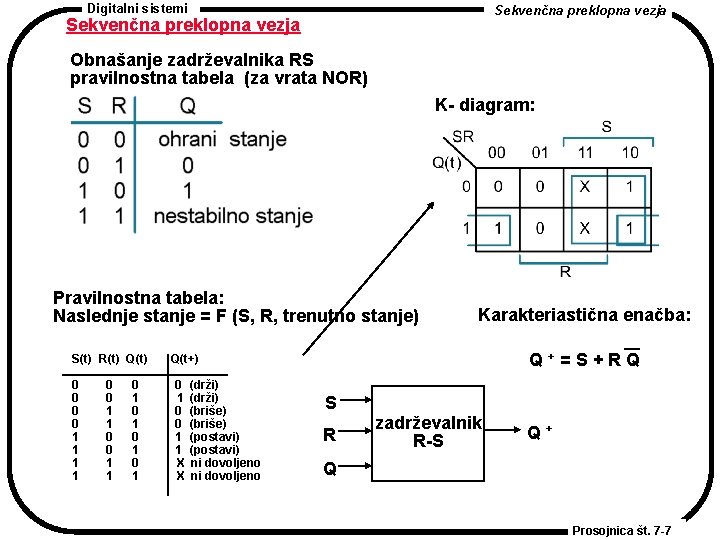
Digitalni sistemi Sekvenčna preklopna vezja Obnašanje zadrževalnika RS pravilnostna tabela (za vrata NOR) K- diagram: Pravilnostna tabela: Naslednje stanje = F (S, R, trenutno stanje) S(t) R(t) Q(t) 0 0 1 1 0 1 0 1 Karakteriastična enačba: Q+=S+RQ Q(t+) 0 1 0 0 1 1 X X (drži) (briše) (postavi) ni dovoljeno S R zadrževalnik R-S Q+ Q Prosojnica št. 7 -7

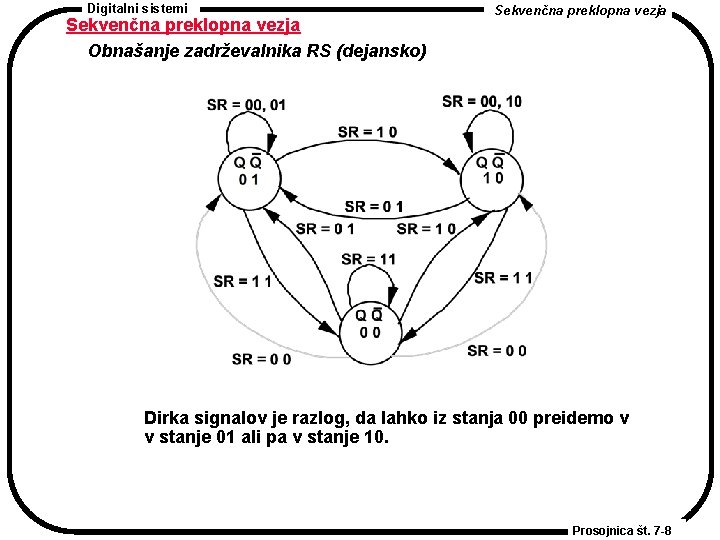
Digitalni sistemi Sekvenčna preklopna vezja Obnašanje zadrževalnika RS (dejansko) Sekvenčna preklopna vezja Dirka signalov je razlog, da lahko iz stanja 00 preidemo v v stanje 01 ali pa v stanje 10. Prosojnica št. 7 -8

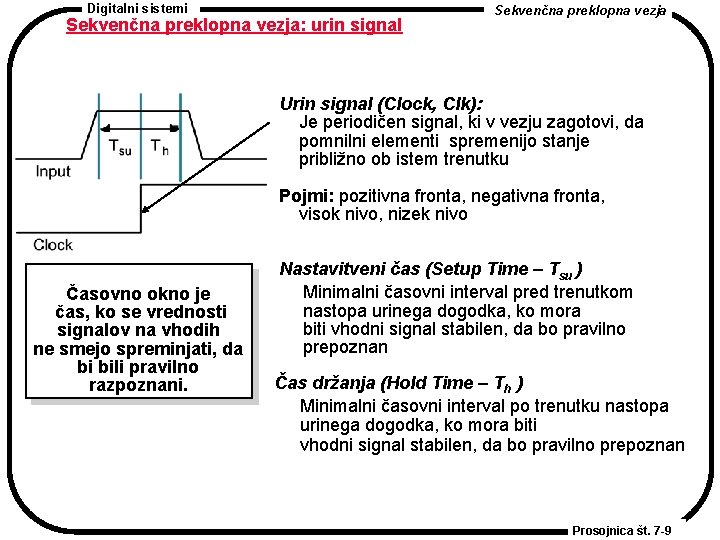
Digitalni sistemi Sekvenčna preklopna vezja: urin signal Sekvenčna preklopna vezja Urin signal (Clock, Clk): Je periodičen signal, ki v vezju zagotovi, da pomnilni elementi spremenijo stanje približno ob istem trenutku Pojmi: pozitivna fronta, negativna fronta, visok nivo, nizek nivo Časovno okno je čas, ko se vrednosti signalov na vhodih ne smejo spreminjati, da bi bili pravilno razpoznani. Nastavitveni čas (Setup Time – Tsu ) Minimalni časovni interval pred trenutkom nastopa urinega dogodka, ko mora biti vhodni signal stabilen, da bo pravilno prepoznan Čas držanja (Hold Time – Th ) Minimalni časovni interval po trenutku nastopa urinega dogodka, ko mora biti vhodni signal stabilen, da bo pravilno prepoznan Prosojnica št. 7 -9

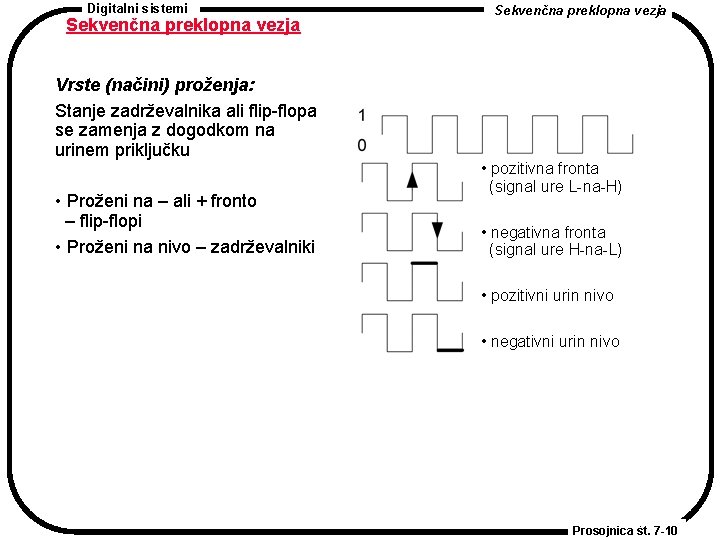
Digitalni sistemi Sekvenčna preklopna vezja Vrste (načini) proženja: Stanje zadrževalnika ali flip-flopa se zamenja z dogodkom na urinem priključku • Proženi na – ali + fronto – flip-flopi • Proženi na nivo – zadrževalniki Sekvenčna preklopna vezja • pozitivna fronta (signal ure L-na-H) • negativna fronta (signal ure H-na-L) • pozitivni urin nivo • negativni urin nivo Prosojnica št. 7 -10

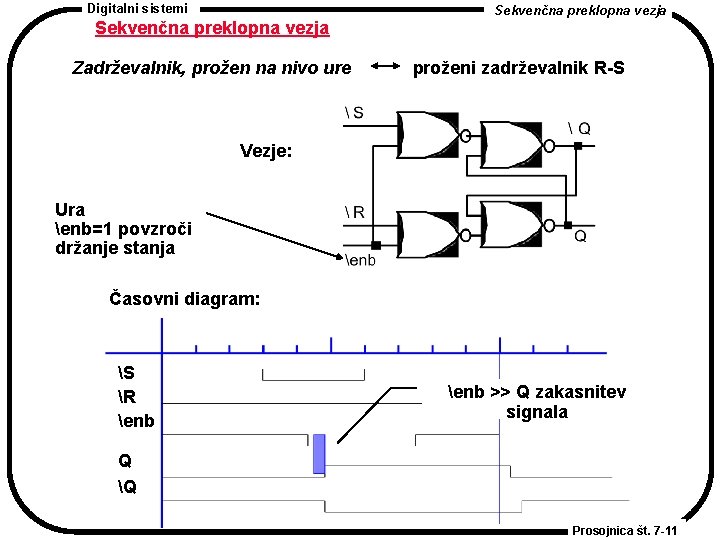
Digitalni sistemi Sekvenčna preklopna vezja Zadrževalnik, prožen na nivo ure proženi zadrževalnik R-S Vezje: Ura enb=1 povzroči držanje stanja Časovni diagram: S R enb >> Q zakasnitev signala Q Q Prosojnica št. 7 -11

Digitalni sistemi Sekvenčna preklopna vezja Pregled obnašanja zadrževalnikov in flip flopov Vhodno/izhodno obnašanje zadrževalnika in flip-flopa Vrsta pomn. celce trenutek branja vhoda zadrževalnik (brez ure) ob vsakem trenutku zadrževalnik prožen na nivo visok urin nivo (Tsu, Th okrog negativne urine fronte) zakasnitev širjenja od trenutka spremembe na vhodu Flip flop prožen Na pozitivno fronto prehod ure iz L-na-H (Tsu, Th okoli trenutka vzpenjanja urinega signala) zakasnitev širjenja od trenutka vzpona urinega signala Flip flop prožen prehod ure iz H-na-L Na negativno fronto (Tsu, Th okoli roba trenutka padanja urinega signala) master/slave Flip flop prehod ure iz visokega-na-nizek (Tsu, Th okoli roba padanja urinega signala) trenutek veljavnosti izhoda zakasnitev signala od trenutka spremembe na vhodu zakasnitev širjenja od trenutka padanja urinega signala zakasnitev širjenja od trenutka padanja urinega sig. Prosojnica št. 7 -12

Digitalni sistemi Sekvenčna preklopna vezja Zadrževalniki se odzivajo na spremembe logičnih nivojev na kontrolnih vhodih Primer: G = 1, vrednost si iz vhoda z zakasnitvijo prenese na izhod (Q=D) Flip flopi podatke shanjujejo v trenutku spremembe urinega signala (pri tem šteje sprememba ali L->H ali H->L). Vrednost na izhodu flip flopa ostane nato nespremenjena do naslednje iste spremembe urinega signala. Različni tipi flip-flopov omogočajo različne izvedbe funkcij. Obnašanje posameznega flip-flopa (ali zadrževalnika) opišemo s karakteristično enačbo. Prosojnica št. 7 -13

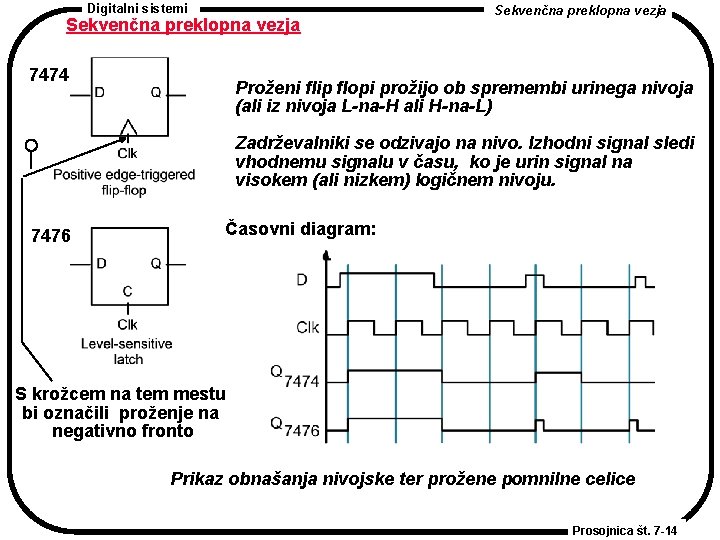
Digitalni sistemi Sekvenčna preklopna vezja 7474 Sekvenčna preklopna vezja Proženi flip flopi prožijo ob spremembi urinega nivoja (ali iz nivoja L-na-H ali H-na-L) Zadrževalniki se odzivajo na nivo. Izhodni signal sledi vhodnemu signalu v času, ko je urin signal na visokem (ali nizkem) logičnem nivoju. 7476 Časovni diagram: S krožcem na tem mestu bi označili proženje na negativno fronto Prikaz obnašanja nivojske ter prožene pomnilne celice Prosojnica št. 7 -14

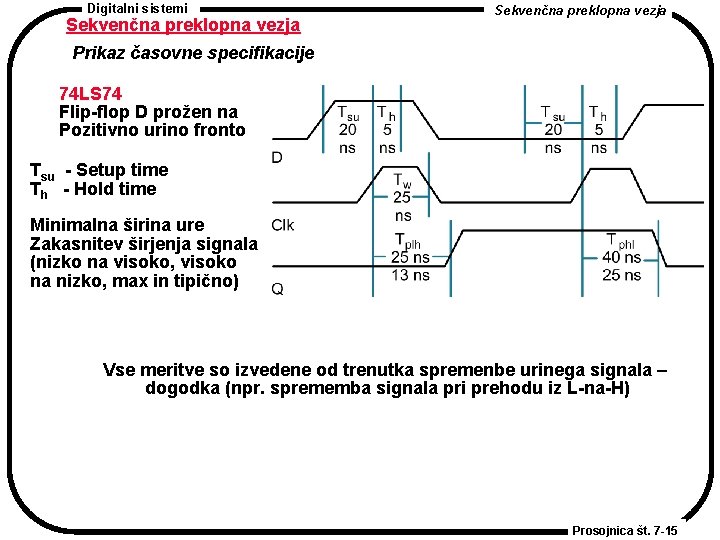
Digitalni sistemi Sekvenčna preklopna vezja Prikaz časovne specifikacije 74 LS 74 Flip-flop D prožen na Pozitivno urino fronto Tsu - Setup time Th - Hold time Minimalna širina ure Zakasnitev širjenja signala (nizko na visoko, visoko na nizko, max in tipično) Vse meritve so izvedene od trenutka spremenbe urinega signala – dogodka (npr. sprememba signala pri prehodu iz L-na-H) Prosojnica št. 7 -15

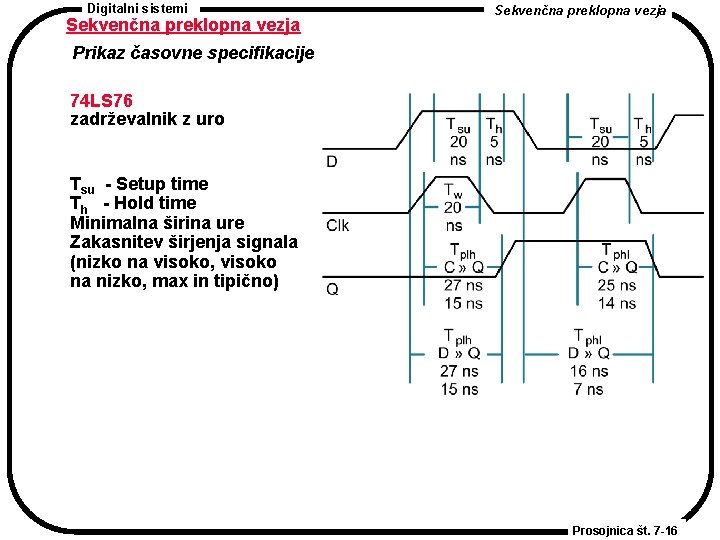
Digitalni sistemi Sekvenčna preklopna vezja Prikaz časovne specifikacije 74 LS 76 zadrževalnik z uro Tsu - Setup time Th - Hold time Minimalna širina ure Zakasnitev širjenja signala (nizko na visoko, visoko na nizko, max in tipično) Prosojnica št. 7 -16

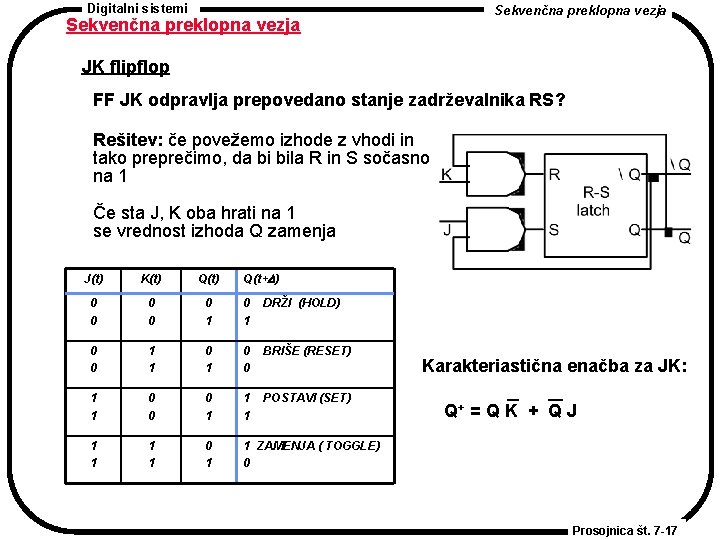
Digitalni sistemi Sekvenčna preklopna vezja JK flipflop FF JK odpravlja prepovedano stanje zadrževalnika RS? Rešitev: če povežemo izhode z vhodi in tako preprečimo, da bi bila R in S sočasno na 1 Če sta J, K oba hrati na 1 se vrednost izhoda Q zamenja Q(t+ ) J(t) K(t) Q(t) 0 0 0 1 DRŽI (HOLD) 0 0 1 1 0 0 BRIŠE (RESET) 1 1 0 0 0 1 1 1 POSTAVI (SET) 1 1 0 1 1 ZAMENJA ( TOGGLE) 0 Karakteriastična enačba za JK: Q+ = Q K + Q J Prosojnica št. 7 -17

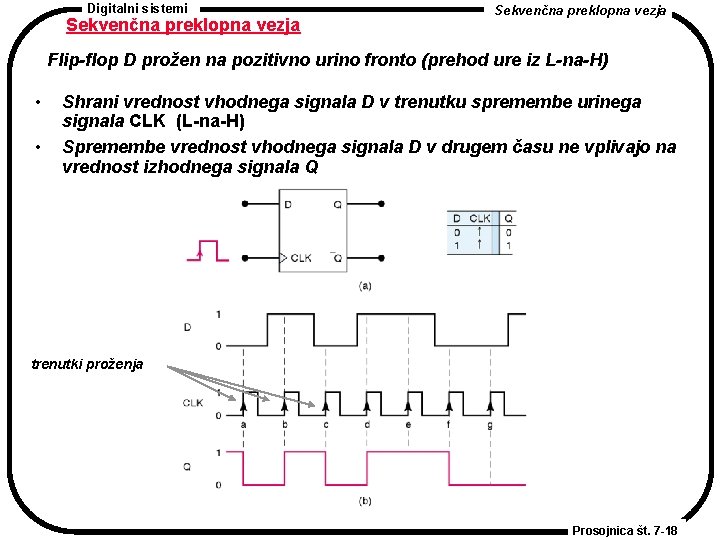
Digitalni sistemi Sekvenčna preklopna vezja Flip-flop D prožen na pozitivno urino fronto (prehod ure iz L-na-H) • • Shrani vrednost vhodnega signala D v trenutku spremembe urinega signala CLK (L-na-H) Spremembe vrednost vhodnega signala D v drugem času ne vplivajo na vrednost izhodnega signala Q trenutki proženja Prosojnica št. 7 -18

Digitalni sistemi Sekvenčna preklopna vezja Flip flop JK prožen na pozitivno fronto ure CLK (prehod ure iz L-na-H) a) vezje flip flopa JK b) grafični simbol FF JK lahko izvedemo tudi z flip-flopom D J K CLK Q vhod J postavlja izhodno vrednost Q 0 0 1 1 vhod K briše izhodno vrednost Q J = K = 1 -> invertira vrednost na izhodu Q 0 1 Q’ Q 0’ 0 1 1 0 zamenja prehod ure Prosojnica št. 7 -19

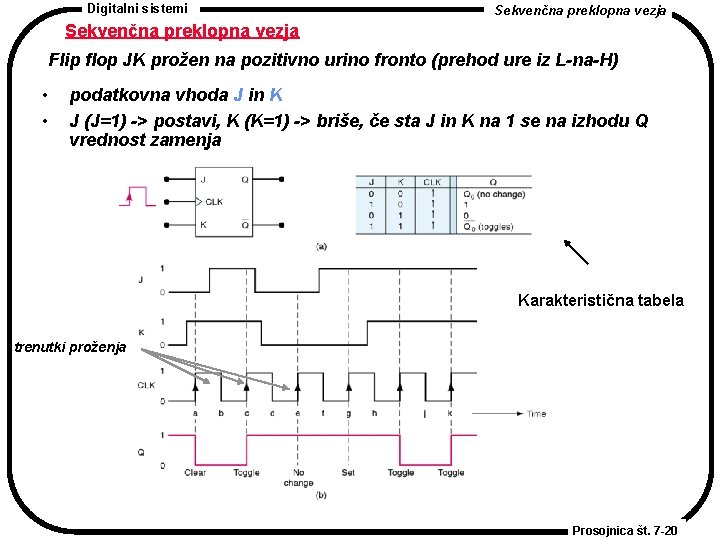
Digitalni sistemi Sekvenčna preklopna vezja Flip flop JK prožen na pozitivno urino fronto (prehod ure iz L-na-H) • • podatkovna vhoda J in K J (J=1) -> postavi, K (K=1) -> briše, če sta J in K na 1 se na izhodu Q vrednost zamenja Karakteristična tabela trenutki proženja Prosojnica št. 7 -20

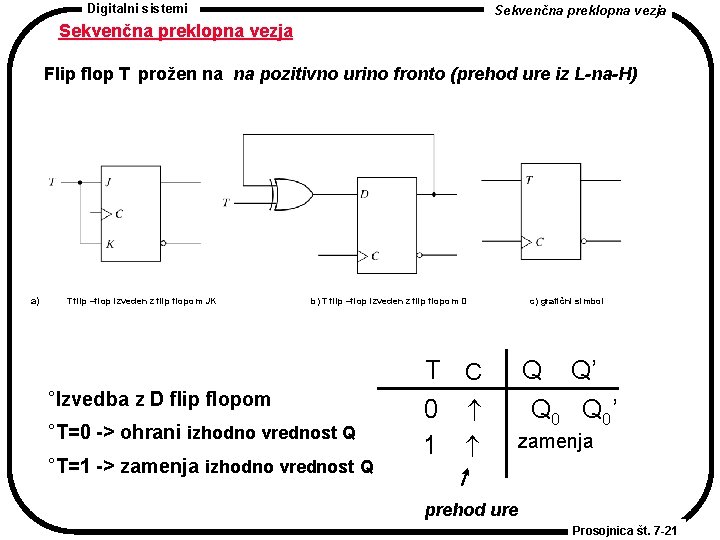
Digitalni sistemi Sekvenčna preklopna vezja Flip flop T prožen na na pozitivno urino fronto (prehod ure iz L-na-H) °Izvedba z D flip flopom °T=0 -> ohrani izhodno vrednost Q a) °T=1 -> zamenja izhodno b) T flipvrednost –flop izveden z flip. Q flopom D T flip –flop izveden z flip flopom JK °Izvedba z D flip flopom °T=0 -> ohrani izhodno vrednost Q °T=1 -> zamenja izhodno vrednost Q T C 0 1 c) grafični simbol Q Q’ Q 0’ zamenja prehod ure Prosojnica št. 7 -21

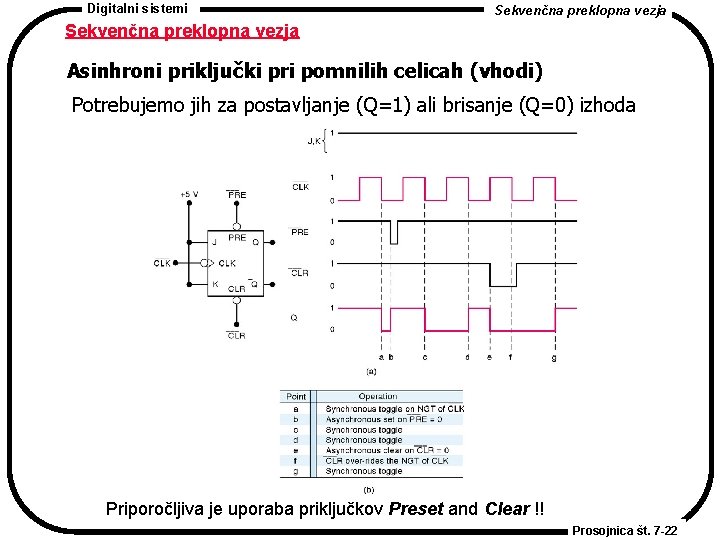
Digitalni sistemi Sekvenčna preklopna vezja Asinhroni priključki pri pomnilih celicah (vhodi) Potrebujemo jih za postavljanje (Q=1) ali brisanje (Q=0) izhoda Priporočljiva je uporaba priključkov Preset and Clear !! Prosojnica št. 7 -22

Digitalni sistemi Uporaba pomnilnih elementov Sekvenčna preklopna vezja Kako izbirati najprimernejši tip pomnilnega elementa? RS zadrževalnik z uro: kot ni priporočljiv pomnilni element za urin signal visoke frekvence! Osnovni gradnik za izvedbo drugih vrst flip flopov JK flip flop: najbolj sestranski, primeren za implementacijo flip-flopa D in T dobra stran: zahteva manjše števil elementov za izvedbo vezja slaba stran: dva vhoda povečata število povezav v vezju D flip flop: dobra stran: zahteva majhno število povezav v vezju, zelo je priljubljen pri načrtovanju pri tehnologijah VLSI enostavno načrtovanje sekvenčnega vezja primeren je za izvedbo pomnilnih registrov T flip flop: dejansko ne obstaja, izvedemo ga s flip-flopom JK; je najprimernejši za uporabo v števnikih Prosojnica št. 7 -23

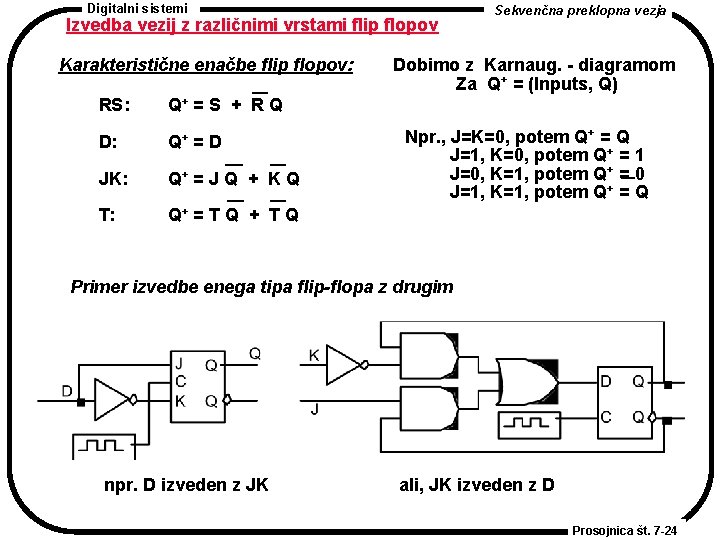
Digitalni sistemi Izvedba vezij z različnimi vrstami flip flopov Karakteristične enačbe flip flopov: RS: Q+ = S + R Q D: Q+ = D JK: Q+ = J Q + K Q T: Q+ = T Q + T Q Sekvenčna preklopna vezja Dobimo z Karnaug. - diagramom Za Q+ = (Inputs, Q) Npr. , J=K=0, potem Q+ = Q J=1, K=0, potem Q+ = 1 J=0, K=1, potem Q+ = 0 J=1, K=1, potem Q+ = Q Primer izvedbe enega tipa flip-flopa z drugim npr. D izveden z JK ali, JK izveden z D Prosojnica št. 7 -24

Digitalni sistemi Izvedba vezij z različnimi vrstami flip flopov Postopek načrtovanja Sekvenčna preklopna vezja Vzbujevalna tabela: kakšne vrednosti na vhodnih priključkih potrebujemo da dosežemo želene prehode stanj? Primer: izvedimo FF D z FF JK : 1) Podamo obnašanje FF D s Karnaugovim diagramom Q+ = (D, Q) (glej vzbujevalno tabelo iz katere tvorimo K-diagram) 2) Sestavimo K-diagrama za vhoda J in K z enakimi vrednostmi (D, Q) 3) Popolnimo K-diagram s primernimi vrednostmi za vhoda J in K Da bi povzročili spremembe stanja kot originalni K diagram Npr. D = Q= 0, Q+ = 0 potem J = 0, K = X Prosojnica št. 7 -25

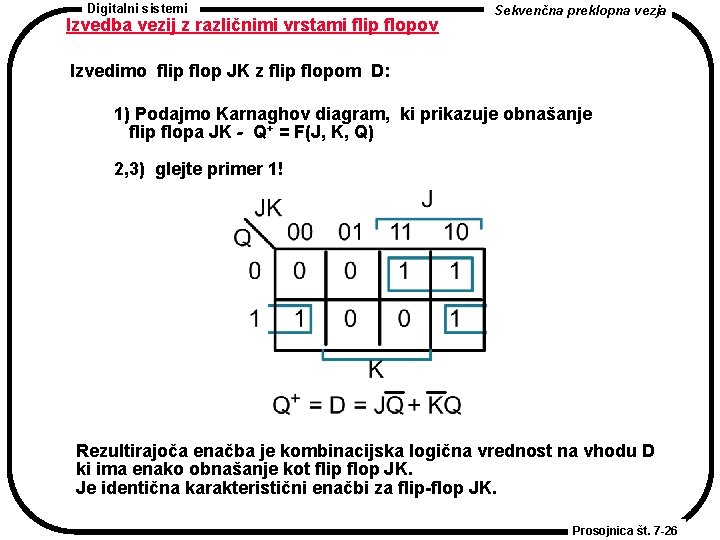
Digitalni sistemi Izvedba vezij z različnimi vrstami flip flopov Sekvenčna preklopna vezja Izvedimo flip flop JK z flip flopom D: 1) Podajmo Karnaghov diagram, ki prikazuje obnašanje flip flopa JK - Q+ = F(J, K, Q) 2, 3) glejte primer 1! Rezultirajoča enačba je kombinacijska logična vrednost na vhodu D ki ima enako obnašanje kot flip flop JK. Je identična karakteristični enačbi za flip-flop JK. Prosojnica št. 7 -26

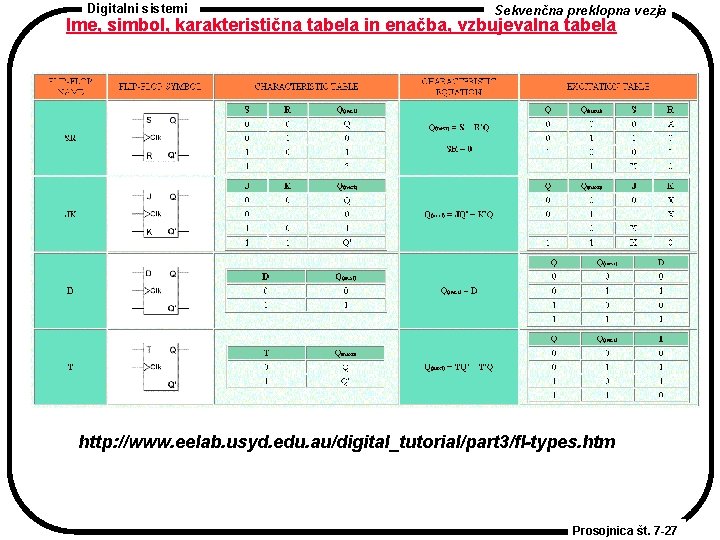
Digitalni sistemi Sekvenčna preklopna vezja Ime, simbol, karakteristična tabela in enačba, vzbujevalna tabela http: //www. eelab. usyd. edu. au/digital_tutorial/part 3/fl-types. htm Prosojnica št. 7 -27

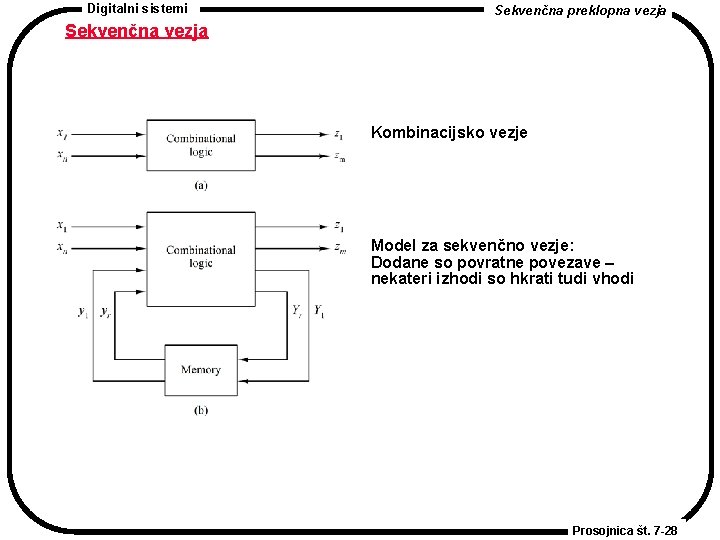
Digitalni sistemi Sekvenčna preklopna vezja Sekvenčna vezja Kombinacijsko vezje Model za sekvenčno vezje: Dodane so povratne povezave – nekateri izhodi so hkrati tudi vhodi Prosojnica št. 7 -28

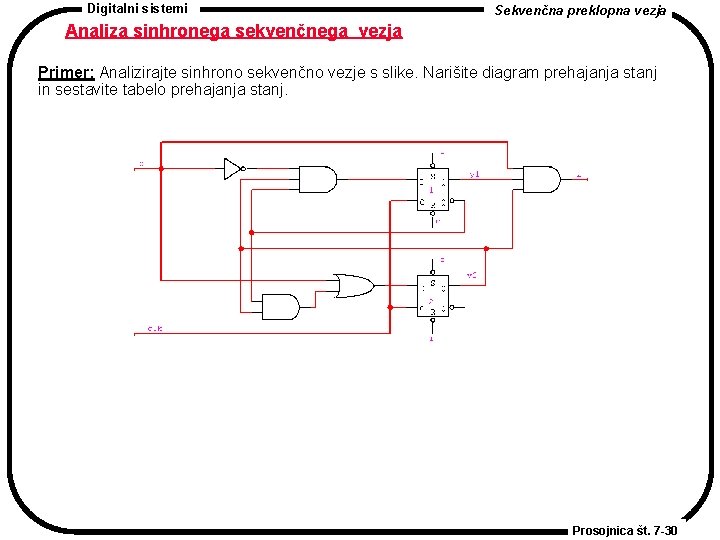
Digitalni sistemi Sekvenčna preklopna vezja Analiza sinhronega sekvenčnega vezja Problem: Izvedimo analizo (teoretično) vezja. Ugotoviti želimo, kako se bo vezje obnašalo. Analizo bomo izvededli v naslednjih korakih. 1. 2. 3. 4. Vsaki pomnilni celici v (sinhronem) sekvenčnem vezju priredimo spremenljivko stanja (npr. y 1, y 2, . . ) Za vsako pomnilno celico zapišemo vhodne vzbujevalne enačbe. Zapišemo tudi izhodne enačbe vezja. Vhodne vzbujevalne enačbe vstavimo v karaktereistične enačbe uporabljenih pomnilnih celic, da dobimo enačbe za naslednja stanja (Q+). Iz enačb za naslednja stanja in iz izhodnih enačb sestavimo tabelo prehajanja stanj in narišemo časovni diagram, s katerim podamo obnašanje vezja. Prosojnica št. 7 -29

Digitalni sistemi Sekvenčna preklopna vezja Analiza sinhronega sekvenčnega vezja Primer: Analizirajte sinhrono sekvenčno vezje s slike. Narišite diagram prehajanja stanj in sestavite tabelo prehajanja stanj. Prosojnica št. 7 -30

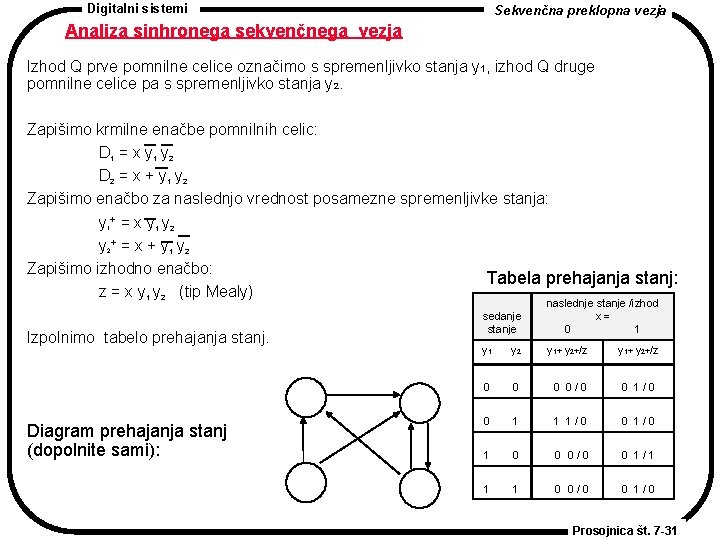
Digitalni sistemi Sekvenčna preklopna vezja Analiza sinhronega sekvenčnega vezja Izhod Q prve pomnilne celice označimo s spremenljivko stanja y 1, izhod Q druge pomnilne celice pa s spremenljivko stanja y 2. Zapišimo krmilne enačbe pomnilnih celic: D 1 = x y 1 y 2 D 2 = x + y 1 y 2 Zapišimo enačbo za naslednjo vrednost posamezne spremenljivke stanja: y + = x y 1 y 2+ = x + y 1 y 2 Zapišimo izhodno enačbo: Tabela prehajanja stanj: z = x y 1 y 2 (tip Mealy) 1 Izpolnimo tabelo prehajanja stanj. Diagram prehajanja stanj (dopolnite sami): sedanje stanje naslednje stanje /izhod x= 0 1 y 2 y 1+ y 2+/z 0 0/0 0 1 1 1/0 0 1/0 1 0 0 0/0 0 1/1 1 1 0 0/0 0 1/0 Prosojnica št. 7 -31

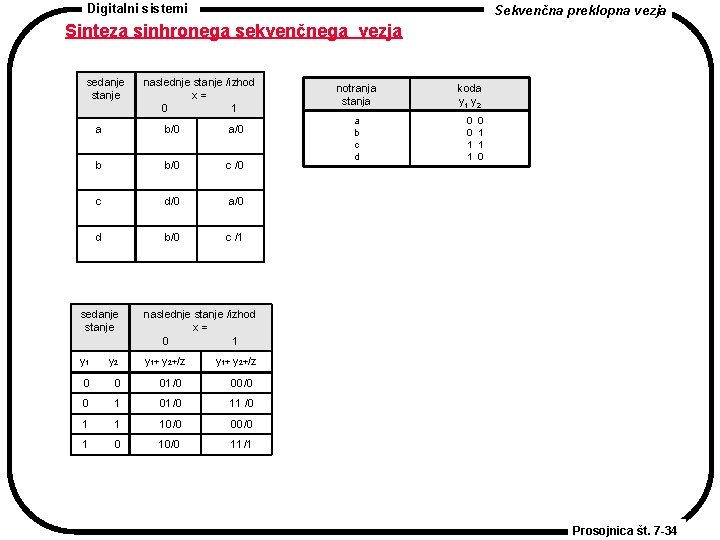
Digitalni sistemi Sekvenčna preklopna vezja Sinteza sinhronega sekvenčnega vezja Problem: Podano je zahtevano obnašanje sinhronega sekvenčnega vezja. Izpeljati želimo čimbolj ekonomično strukturo z danim obnašanjem. Koraki sinteze so: 1. 2. 3. 4. 5. Iz besednega opisa problema sestavimo diagram ali tabelo prehajanja stanj. Iz sestavljenega diagrama ali tabele prehajanja stanj odstranimo morebitna redundantna stanja. (Postopek za odkrivanje in odpravljanje redundatnih stanj bomo obravnavavali v naslednjem poglavju. Tabele in diagrami prehajanja stanj v tem poglavju bodo sestavljeni tako, da ne bodo vsebovali redundatnih stanj. ) Stanja zakodiramo (označimo). P stanj zakodiramo s p spremenljivkami stanj Y= y 1, y 2, y 3, …, , yp , kjer je 2 p ≥ P. Dobimo zakodiran diagram ali zakodirano tabelo prehajanja stanj. Izberemo tip pomnilniške celice. Izpeljemo funkcije za primarne izhode in sekundarne izhode (vzbujevalne enačbe). Vezje narišemo. Prosojnica št. 7 -32

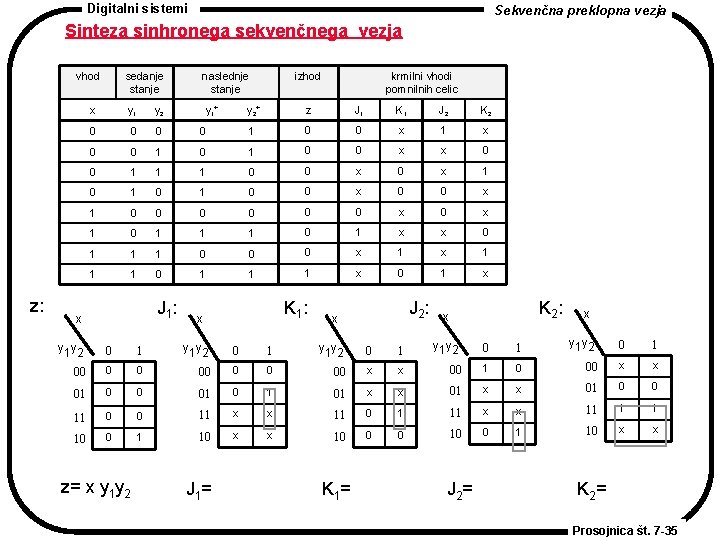
Digitalni sistemi Sekvenčna preklopna vezja Sinteza sinhronega sekvenčnega vezja Primer: Potrebujemo sinhrono sekvenčno vezje z vhodom x in izhodom z, ki generira izhod z=1, ko se na vhodu odkrije sekvenca 0101. V vseh drugih časih je z=0. Npr. , za vhodno sekvenco 010101 je izhodna sekvenca 000101. Uporabimo pomnilne celice JK. Prosojnica št. 7 -33

Digitalni sistemi Sekvenčna preklopna vezja Sinteza sinhronega sekvenčnega vezja sedanje stanje naslednje stanje /izhod x= 0 1 a b/0 a/0 b b/0 c d/0 a/0 d b/0 c /1 sedanje stanje naslednje stanje /izhod x= 0 1 y 2 y 1+ y 2+/z 0 0 01/0 00/0 0 1 01/0 11 /0 1 1 10/0 00/0 1 0 10/0 11/1 notranja stanja koda y 1 y 2 a b c d 0 0 1 1 0 y 1+ y 2+/z Prosojnica št. 7 -34

Digitalni sistemi Sekvenčna preklopna vezja Sinteza sinhronega sekvenčnega vezja vhod z: sedanje stanje naslednje stanje x y 1 y 2 y 1+ 0 0 0 izhod krmilni vhodi pomnilnih celic y 2+ z J 1 K 1 J 2 K 2 0 1 0 0 x 1 0 1 0 0 x x 0 1 1 1 0 0 x 1 0 0 0 x 0 x 1 0 1 1 1 0 1 x x 0 1 1 1 0 0 0 x 1 1 1 0 1 1 1 x 0 1 x J 1: x x K 1: J 2: x x 01 0 0 x x 11 1 1 0 1 10 x x 01 x 0 1 11 0 0 1 y 1 y 2 0 1 00 0 0 00 x x 01 0 0 01 0 1 01 x 11 0 0 11 x x 11 10 0 1 10 x x 10 K 1= 00 1 y 1 y 2 J 2= y 1 y 2 1 00 1 x 0 1 0 J 1= y 1 y 2 0 y 1 y 2 z= x y 1 y 2 K 2: x K 2= Prosojnica št. 7 -35

Digitalni sistemi Sekvenčna preklopna vezja Avtomati Avtomat je skupek množic in relacij med njimi. Avtomate obravnava teorija o avtomatih. Avtomati se uporabljajo na najrazličnejših področjih: v digitalnih sistemih, računalništvu, matematiki, robotiki, jezikoslovju, družbenih vedah, itd. Realizaciji avtomata lahko rečemo informacijski stroj. Sekvenčna vezja, ki smo jih že obdelali, ustrezajo informacijskemu stroju ali realizaciji avtomata. Glavni razvijalci teorije o avtomatih so Huffman, Moore, Mealy, Turing in von Neumann v letih od 1936 do 1060. Od vseh avtomatov so najbolj razširjeni končni avtomati. Najbolj splošen je Touringov stoj oz. avtomat. Po splošnosti se med obe skrajnosti uvrščajo vmesni avtomati (med njimi so potisni, skladovni in linearno ločljivi avtomati). Zanimali nas bodo samo deterministični avtomati. Med vsemi avtomati sta najbolj znana Mealyjev in Moorov avtomat je samo posebna oblika Mealyevega avtomata. Izhodna vrednost se pri Moorovem avtomatu lahko spremeni samo s spremembo stanj, pri Mealyjevemu pa še tudi s spremembo vhoda. Končni avtomati – osnovne definicije Def. : Končni avtomat tipa Mealy A ME(krajše Mealyjev avtomat) je peterica: AME = (I; Y; O; δ; λ), kjer je I končna in neprazna množica vhodnih črk - vhodna abeceda, Y končna in neprazna množica notranjih črk (stanj) avtomata - notranja abeceda, O končna in neprazna množica izhodnih črk - izhodna abeceda, δ: I x Y -> Y funkcija prehajanja stanj, λ: I x Y -> O izhodna funkcija. Velikokrat v deniciji dodamo tudi začetno stanje y 0єY. To je stanje, v katerem se avtomat nahaja v začetku delovanja. Prosojnica št. 7 -36

Digitalni sistemi Sekvenčna preklopna vezja Avtomati Funkcijo prehajanja stanj in izhodno funkcijo lahko izrazimo na naslednji način: y+ = δ(i; y); i I; y Y in o = λ(i; y); i I; y Y; o O, kjer je i sedanja vhodna črka, s sedanja notranja črka (sedanje stanje), y+ naslednja notranja črka (naslednje stanje) in o sedanja izhodna črka avtomata. δ je casovna preklopna funkcija in λ navadna preklopna funkcija. Def. : Končni avtomat tipa Moore AMO (krajše Moorov avtomat) je poseben primer Mealyjevega avtomata, in sicer z enostavnejšo izhodno funkcijo: λ : Y -> O, tj. o = λ(y), y Y; o O, V Mealyjevem avtomatu je torej sedanja izhodna črka odvisna od sedanje vhodne črke in sedanjega stanja, v Moorovem pa samo od sedanjega stanja avtomata. Končni avtomat je determinističen, ker za katerakoli stanja y; y 1; y 2 Y in poljubno vhodno črko i I velja: če λ(i; y) = y 1 in δ(i; y) = y 2, potem y 1 = y 2. Če primerjamo definicijo končnega avtomata z modelom sinhronega sekvenčnega vezja, ugotovimo, da predstavlja sinhrono sekvenčno vezje možno realizacijo avtomata. Funkcija prehajanja stanj je realizirana z vzbujevalnimi enačbami za vhode pomnilnih celic, izhodna funkcija pa na primarnih izhodih kombinacijske logike C. Prosojnica št. 7 -37

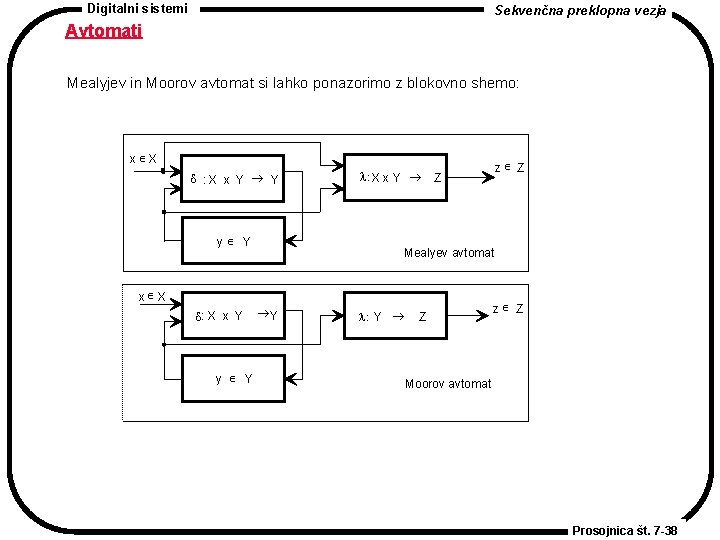
Digitalni sistemi Sekvenčna preklopna vezja Avtomati Mealyjev in Moorov avtomat si lahko ponazorimo z blokovno shemo: x X d : X x Y ® Y y Y Mealyev avtomat x X d: X x Y y Y z Z l: X x Y ® Z ® Y l: Y ® Z z Z Moorov avtomat Prosojnica št. 7 -38

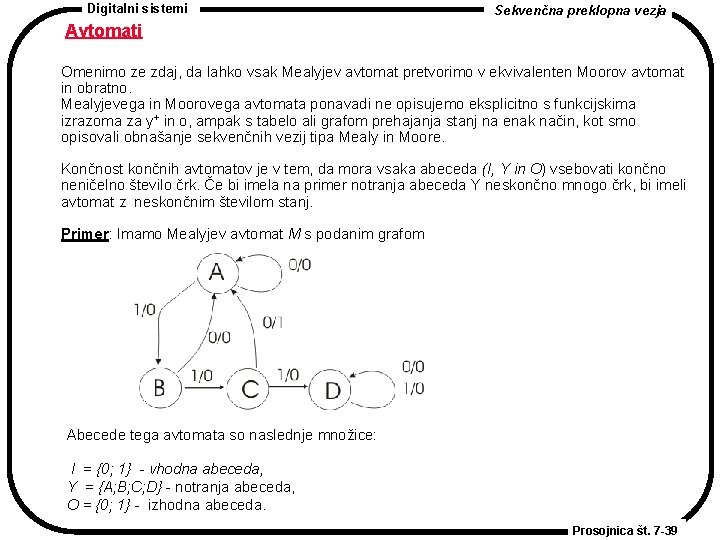
Digitalni sistemi Sekvenčna preklopna vezja Avtomati Omenimo ze zdaj, da lahko vsak Mealyjev avtomat pretvorimo v ekvivalenten Moorov avtomat in obratno. Mealyjevega in Moorovega avtomata ponavadi ne opisujemo eksplicitno s funkcijskima izrazoma za y+ in o, ampak s tabelo ali grafom prehajanja stanj na enak način, kot smo opisovali obnašanje sekvenčnih vezij tipa Mealy in Moore. Končnost končnih avtomatov je v tem, da mora vsaka abeceda (I, Y in O) vsebovati končno neničelno število črk. Če bi imela na primer notranja abeceda Y neskončno mnogo črk, bi imeli avtomat z neskončnim številom stanj. Primer: Imamo Mealyjev avtomat M s podanim grafom Abecede tega avtomata so naslednje množice: I = {0; 1} - vhodna abeceda, Y = {A; B; C; D} - notranja abeceda, O = {0; 1} - izhodna abeceda. Prosojnica št. 7 -39

Digitalni sistemi Sekvenčna preklopna vezja Avtomati Naj bo X poljubna množica. Z X* označimo množico vseh končnih zaporedij elementov iz množice X, vključno s praznim. Sekvenca (ali beseda) je končno (lahko prazno) zaporedje črk iz ene od abeced. Vhodna sekvenca je zaporedje w I. Izhodna sekvenca je zaporedje O. Na končni avtomat lahko gledamo kot na pretvornik vhodne sekvence v izhodno. Končni avtomat lahko uporabimo za reševanje vseh tistih problemov, ki se dajo izraziti s pretvorbo sekvenc. Za zgornji avtomat M predpostavimo, da je njegovo začetno stanje A. Potem pretvori vhodno sekvenco w = 110 v izhodno sekvenco = 001. Pomembna naloga končnega avtomata je, da odloči, ali je dana vhodna sekvenca element neke vnaprej specificirane množce sekvenc. Avtomat izvrši to nalogo tako, da sprejme tiste sekvence, ki so elementi množice, in zavrne tiste, ki to niso. Za avtomat, ki se priče izvajati v svojem začetnem stanju, pravimo, da sprejme vhodno sekvenco, če postavi izhod na 1, ko sprejme zadnjo črko vhodne sekvence. Avtomat M na primer sprejme sekvenci 110 in 0110 ter zavrne sekvenco 01100. Če je y+ = (i; y), pravimo, da je stanje y+ i-naslednik stanja s (pišemo y -> y+) Stanje B je na primer 1 -naslednik stanja A v avtomatu M, ker iz stanja A pridemo v B, če damo na vhod 1. V splošnem, če vhodna sekvenca w popelje avtomat iz stanja yi v stanje yj, pravimo, da je stanje yj w-naslednik stanja yi. V avtomatu M je na primer stanje D 111 -naslednik stanja A. Če za vsak par stanj yi; yj končnega avtomata obstaja vhodna sekvenca, ki popelje avtomat iz yi v yj , pravimo, da je avtomat krepko povezan. Prosojnica št. 7 -40

Digitalni sistemi Sekvenčna preklopna vezja Avtomati: Ekvivalenca stanj in minimizacija avtomata Pri tvorbi grafa ali tabele prehajanja stanj končnega avtomata se pogosto zgodi, da vsebuje redundantna ali odvečna stanja. Število pomnilniških celic, ki je potrebno za realizacijo avtomata, je neposredno odvisno od števila stanj. Zaradi tega minimizacija števila stanj v mnogih primerih zmanjša kompleksnost in ceno realizacije. Ekvivalenca stanj in avtomatov Def. : Končna avtomata A 1 in A 2 (istega tipa) sta ekvivalentna, če in samo če: 1. I 1 = I 2; O 1 = O 2 in 2. Če w 1 = w 2, potem 1 = 2, za vsak wi Ii*, 1 = Oi*, i=1, ; tj. če za vsako možno vhodno sekvenco dobimo enako izhodno sekvenco v obeh avtomatih. Def. : Stanji ya in yb končnega avtomata AME = (I; Y; O; δ; λ) sta ekvivalentni, če in samo če sta avtomata A z začetnim stanjem ya in A z začetnim stanjem yb ekvivalentna. Def. : Stanji ya in yb končnega avtomata A sta razločljivi, če in samo če obstaja vsaj ena končna vhodna sekvenca, ki povzroči različni izhodni sekvenci za začetni stanji ya in yb v avtomatu A. Sekvenca, ki razloči ti stanji, se imenuje razločevalna sekvenca para stanj (ya; yb). Def. : Če za stanji ya in yb končnega avtomata A razločljivi, potem sta razločljivi s vhodno sekvenco dolžine n -1, pri čemer je n število stanj avtomata A. Izrek: Če stanji nista k-razločljivi, pravimo, da sta k-ekvivalentni. Izrek: Izrek Stanji, ki sta k-ekvivalentni, sta tudi r-ekvivalentni za vse r < k. Če stanji k-ekvivalentni za vsak k, sta ekvivalentni. Prosojnica št. 7 -41

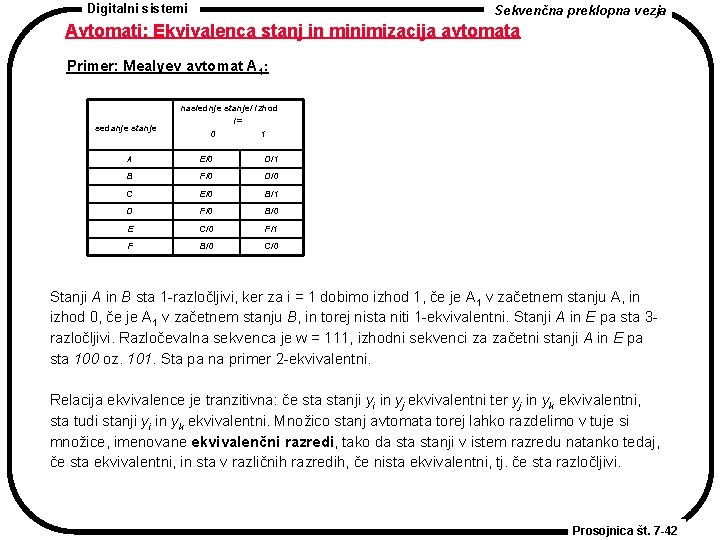
Digitalni sistemi Sekvenčna preklopna vezja Avtomati: Ekvivalenca stanj in minimizacija avtomata Primer: Mealyev avtomat A 1: sedanje stanje naslednje stanje/ izhod i= 0 1 A E/0 D/1 B F/0 D/0 C E/0 B/1 D F/0 B/0 E C/0 F/1 F B/0 C/0 Stanji A in B sta 1 -razločljivi, ker za i = 1 dobimo izhod 1, če je A 1 v začetnem stanju A, in izhod 0, če je A 1 v začetnem stanju B, in torej nista niti 1 -ekvivalentni. Stanji A in E pa sta 3 razločljivi. Razločevalna sekvenca je w = 111, izhodni sekvenci za začetni stanji A in E pa sta 100 oz. 101. Sta pa na primer 2 -ekvivalentni. Relacija ekvivalence je tranzitivna: če stanji yi in yj ekvivalentni ter yj in yk ekvivalentni, sta tudi stanji yi in yk ekvivalentni. Množico stanj avtomata torej lahko razdelimo v tuje si množice, imenovane ekvivalenčni razredi, tako da stanji v istem razredu natanko tedaj, če sta ekvivalentni, in sta v različnih razredih, če nista ekvivalentni, tj. če sta razločljivi. Prosojnica št. 7 -42

Digitalni sistemi Sekvenčna preklopna vezja Avtomati: Ekvivalenca stanj in minimizacija avtomata Procedura minimizacije stanj Def. : Vzemimo množico Y = {y 1, … , yr }. Iz elementov te množice je mogoče tvoriti 2 r različnih podmnožic. Če iz teh podmnožic izberemo takšne neprazne podmnožice, da za njih velja B 1 U B 2 U … U B q = Y , Bi Bj = 0 ; za i; j {1, …, q}, i j, imenujemo množico = {B 1, B 2, …, Bq } particija na množici Y. Elemente Bi imenujemo bloki. Pri q blokih imamo q-bločno particijo. Izrek: Stanji ya in yb končnega avtomata A sta ekvivalentni natanko tedaj, če: 1. (a) Mealy: i I; λ(ya; i) = λ(yb; i), tj. če za vsak vhodni simbol dobimo enak izhodni simbol za ya in za yb; (b) Moore: λ(ya) = λ(yb), tj. če v ya in yb dobimo enak izhodni simbol, • in i I; δ(ya, i) δ(yb, i), tj. Če za vsak vhodni simbol pridemo iz ya in iz yb v naslednji stanji, ki sta med seboj tudi ekvivalentni. Prosojnica št. 7 -43

Digitalni sistemi Sekvenčna preklopna vezja Avtomati: Ekvivalenca stanj in minimizacija avtomata Procedura minimizacije stanj Opišimo proceduro za iskanje množic ekvivalentnih stanj podanega avtomata A, ki temelji na tem izreku. Želen rezultat je taka particija stanj avtomata, da bosta dve stanji v istem bloku, če in samo če sta ekvivalentni. 1. korak: Tvorimo particijo 1, v kateri so v istem bloku 1 -ekvivalentna stanja, v različnih pa 1 -razločljiva, takole: Stanja, ki imajo enake izhode pri vseh možnih vhodih, postavimo v isto podmnožico (Mealy). (Moore: stanja, ki imajo enake izhode, postavimo v isto podmnožico. ) V vseh naslednjih korakih, to je za vsak k > 0, izvajamo naslednji korak: k+1. korak: Tvorimo particijo k+1, v kateri so v istem bloku k + 1 -ekvivalentna stanja, v različnih pa k + 1 - razločljiva, iz particije k takole: v isti blok particije k+1 postavimo tista stanja, ki so v istem bloku particije k in katerih i-nasledniki za i I so tudi v skupnem bloku particije k. Če za neki k dobimo k+1 = k, je procedura končana in k vsebuje množice ekvivalentnih stanj avtomata. imenujemo ekvivalenčna particija. k Primer: minimizacije avtomata A 1 (izveden na predavanju!). Izrek: Ekvivalenčna particija je edinstvena. Lahko ugotovimo tudi, da sta končna avtomata brez določenih začetnih stanj A 1 in A 2 ekvivalentna, če in samo če za vsako stanje v A 1 obstaja ekvivalentno stanje v A 2 in obratno. V praksi se pogosto dogaja, da nekatere kombinacije stanj ali vhodov niso možne. V drugih primerih so prehodi stanj popolnima definirani, toda za nekatere kombinacije stanj in vhodov vrednosti izhodov niso pomembne, zato jih ne specificiramo. Takim avtomatom pravimo nepopolno specificirani avtomati. Pri nepopolno specificiranih avtomatih namesto o ekvivalenci govorimo o kompatibilnosti stanj in avtomatov. Prosojnica št. 7 -44

Digitalni sistemi Sekvenčna preklopna vezja Avtomati: Pretvorba avtomatov iz tipa Mealy v tip Moore in obratno Dva končna avtomata (istega tipa) (z definiranim začetnim stanjem) sta ekvivalentna, če dasta pri enakih vhodnih sekvencah enake izhodne sekvence. V primeru avtomatov AME in AMO pa ekvivalenca ni tako stroga. Omenjena avtomata sta ekvivalentna, če imata pri enakih vhodnih sekvencah enake izhodne sekvence, pri tem pa prva črka na izhodu avtomata AMO ne šteje (tj. ni pomembna). Pretvorba AMO v AME Preprostejša je pretvorba AMO v AME. Stanja in prehodi v AME so enaki onim v AMO. Kadar ima stanje s v AMO izhod o, je vsak prehod v AME v stanje s označen z izhodom o. Izpeljava je naslednja: če potem pri čemer je AMO = (I, Y, O, δ, λMO, y 0), AME = (I, Y, O, δ, λME, y 0); λME(i, y) = λMO(δ(i, y)) za vsak i I y Y. Primer (predavanja). Pretvorba AME v AMO Izpeljava avtomata AMO iz podanega avtomata AME je nekoliko težja. Zgornje izpeljave ne moremo kar preprosto obrniti, ker lahko AME vsebuje stanje y, katerega vhodni prehodi so označeni z različnimi izhodnimi črkami. Da bi obšli to težavo, označimo stanja v avtomatu AMO z vsemi pari stanje-izhod iz množice YME x O iz avtomata AME. Avtomat AMO bo vstopil v stanje (y, o), kadarkoli AME vstopi v stanje y in tvori izhodno črko o. Izpeljava je naslednja: če potem AME = (I, YME, O, δME, λME, y 0), AMO = (I, YMO, O, δMO, λMO, (y 0, O 0)), Prosojnica št. 7 -45

Digitalni sistemi Sekvenčna preklopna vezja Avtomati: Pretvorba avtomatov iz tipa Mealy v tip Moore in obratno pri čemer je YMO = YME x O in o 0 O poljubna izhodna črka: Funkciji δMO in λMO sta definirani na naslednji način: Kadar ima AME prehod ima AMO prehod za vsak o’ 0 O. Kadar ima AME začetno stanje y 0, ima AMO v grafu prehajanja stanj začetno stanje za poljuben o 0 O. Primer (predavanja) Prosojnica št. 7 -46

Digitalni sistemi Sekvenčna preklopna vezja Avtomat: Dekompozicija končnih avtomatov Računanje s particijami Def. : Če sta 1 in 2 particiji na mnozici Y , je “produkt" dobimo s presekom blokov iz 1 s tistimi 2: = 1. 2 particija na Y, ki jo B = B i BJ , B 1 , B 1 1 , B 2 2. Def. : Če sta 1 in 2 particiji na množici Y, je "vsota" = 1 in 2 particija na Y, ki jo dobimo, če združimo bloke particij 1 in 2, ki imajo vsaj en skupen element. Obstajata dve značilni particiji: particija enote E in particija niča ali ničelna particija 0. E ima en blok, v katerem so vsi elementi množice Y, 0 pa ima za vsak element y Y svoj blok. Če je poljubna particija na množici Y , velja: 0 E . = 0. = + = . = E Prosojnica št. 7 -47

Digitalni sistemi Sekvenčna preklopna vezja Avtomat: Dekompozicija končnih avtomatov Def. : Vzemimo, da je = {B 1, B 2, …, Bq} neka particija na množici stanj Y končnega avtomata A z vhodnimi črkami i I in prehajalno relacijo δ. Particija ima substitucijsko značilnost, če velja: δ(i; Bj) Bk za vsak i I; j {1, 2, …, q}. tj. vsa stanja iz istega bloka se za poljubno vhodno črko i preslikajo v stanja, ki so spet skupaj v bloku. Izrek: Particija s substitucijsko značilnostjo, ki ima za poljubno vhodno črko za vsako stanje v bloku B enako izhodno črko, je ekvivalenčna particija. Sedaj se lotimo problema dekompozicije avtomata. Ideja je naslednja. Namesto da bi realizirali celoten avtomat, ga najprej dekomponiramo v manjše avtomate, vsakega izvedemo posebej, nato pa jih med seboj povezemo. Tako dobljeni sestavljeni avtomat se mora navzven obnašati enako kot podani avtomat. Dve osnovni vrsti dekompozicije končih avtomatov sta serijska in paralelna dekompozicija (obravnavali bomo samo dekompozicijo enega avtomata v dva). Prosojnica št. 7 -48

Digitalni sistemi Sekvenčna preklopna vezja Avtomat: Dekompozicija končnih avtomatov Serijska dekompozicija koncnega avtomata Serijska dekompozicija avtomata A na podavtomata Aa in Ab je možna le v primeru, če za množico stanj Y avtomata A najdemo particiji a in b tako, da velja a in b = 0 in ima ena od particij a , b substitucijsko značilnost. Paralelna dekompozicija končnega avtomata Paralelna dekompozicija avtomata A na avtomat Aa in Ab obstaja le, če najdemo particiji a in b tako, da velja a in b = 0 in ima tako particija a kot particija b substitucijsko značilnost. Prosojnica št. 7 -49