Digital Systems Department of Computer Science and Information

數位系統 Digital Systems Department of Computer Science and Information Engineering, Chaoyang University of Technology 朝陽科技大學資 系 Speaker: Fuw-Yi Yang 楊伏夷 伏夷非征番, 道德經 察政章(Chapter 58) 伏者潛藏也 道紀章(Chapter 14) 道無形象, 視之不可見者曰夷 Fuw-Yi Yang 1

Text Book: Digital Design 4 th Ed. Chap 3 Gate-Level Minimization 3. 1 Introduction 3. 2 The Map Method 3. 3 Four-Variable Map 3. 4 Five-Variable Map 3. 5 Production-of-Sums Simplification 3. 6 Don't-Care Conditions 3. 7 NAND and NOR Implementation 3. 8 Other Two-Level Implementation 3. 9 Exclusive-Or Function 3. 10 Hardware Description Language Fuw-Yi Yang 2

Text Book: Digital Design 4 th Ed. Chap 3. 1 Introduction Gate-level minimization refers to the design task of finding an optimal gate-level implementation of the Boolean functions describing a digital circuit. It is important that a designer understand the underlying mathematical description and solution of a problem. Fuw-Yi Yang 3

Text Book: Digital Design 4 th Ed. Chap 3. 2 The Map Method Boolean expression may be simplified by algebraic means as discussed in Section 2. 4. However, this procedure of minimization is awkward because it lacks specific rules to predict each succeeding step in the manipulative process. The map method (also known as the Karnaugh map or K-map) provides a simple, straightforward procedure for minimizing Boolean functions. Fuw-Yi Yang 4

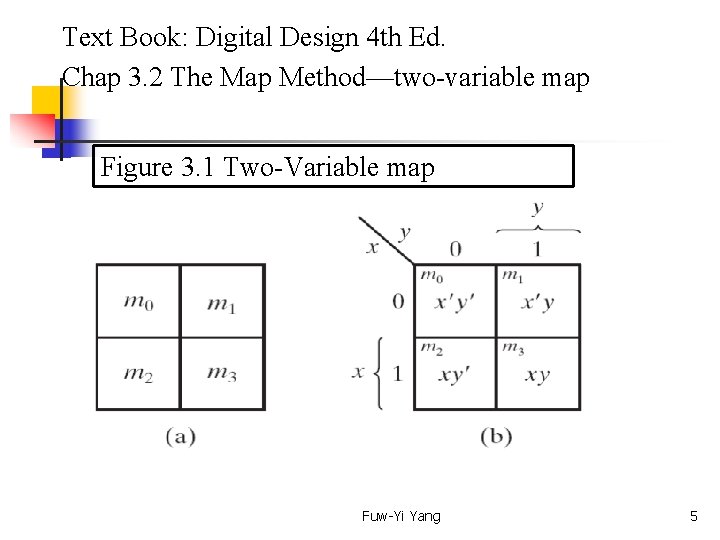
Text Book: Digital Design 4 th Ed. Chap 3. 2 The Map Method—two-variable map Figure 3. 1 Two-Variable map Fuw-Yi Yang 5

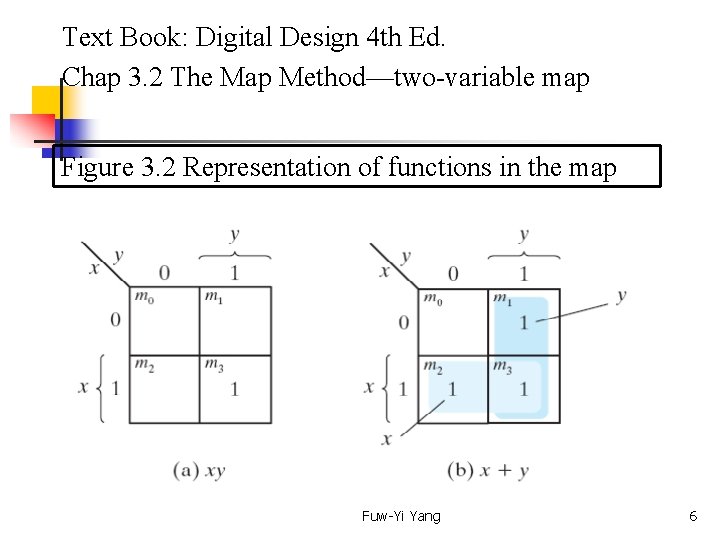
Text Book: Digital Design 4 th Ed. Chap 3. 2 The Map Method—two-variable map Figure 3. 2 Representation of functions in the map Fuw-Yi Yang 6

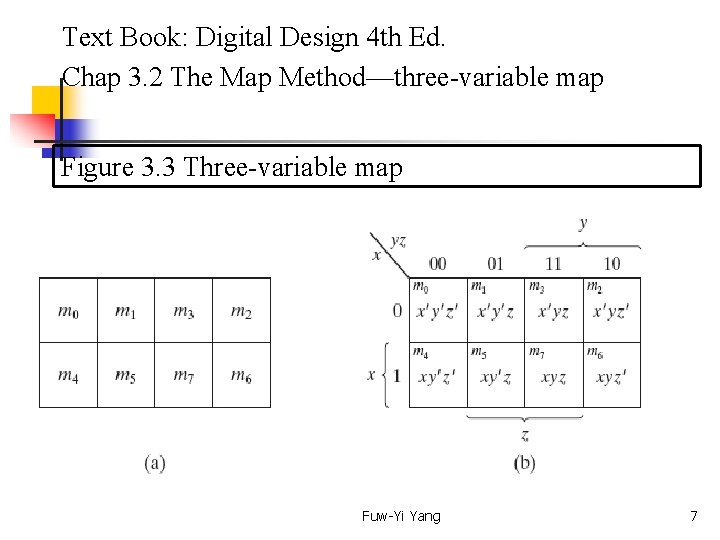
Text Book: Digital Design 4 th Ed. Chap 3. 2 The Map Method—three-variable map Figure 3. 3 Three-variable map Fuw-Yi Yang 7

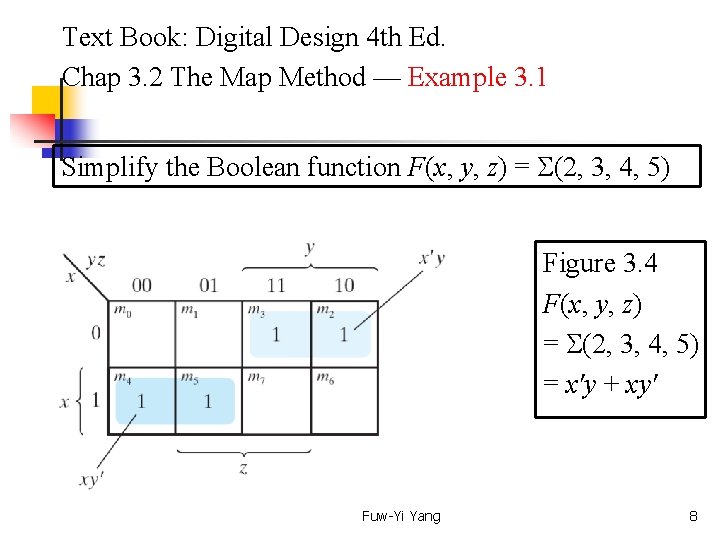
Text Book: Digital Design 4 th Ed. Chap 3. 2 The Map Method — Example 3. 1 Simplify the Boolean function F(x, y, z) = (2, 3, 4, 5) Figure 3. 4 F(x, y, z) = (2, 3, 4, 5) = x'y + xy' Fuw-Yi Yang 8

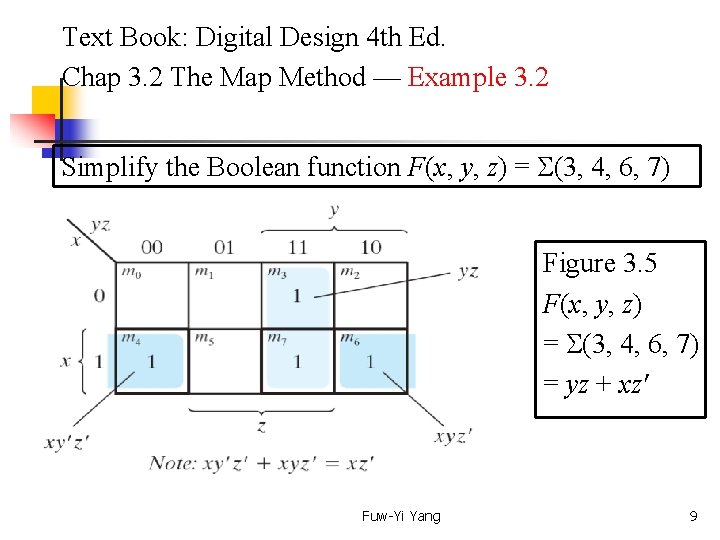
Text Book: Digital Design 4 th Ed. Chap 3. 2 The Map Method — Example 3. 2 Simplify the Boolean function F(x, y, z) = (3, 4, 6, 7) Figure 3. 5 F(x, y, z) = (3, 4, 6, 7) = yz + xz' Fuw-Yi Yang 9

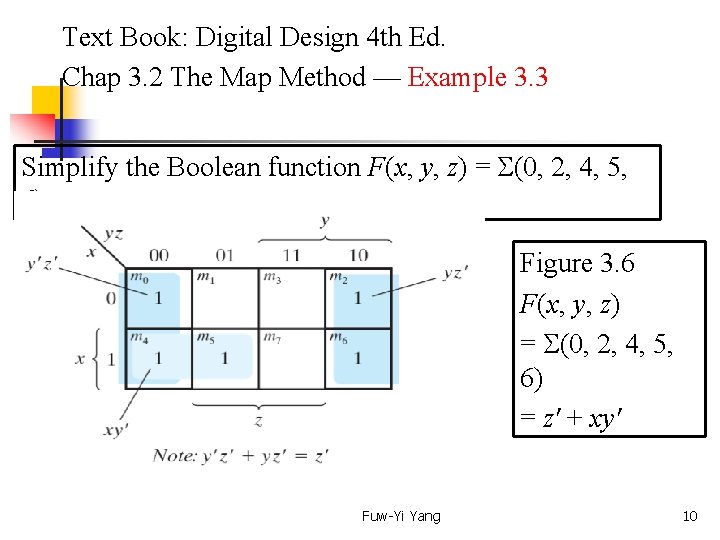
Text Book: Digital Design 4 th Ed. Chap 3. 2 The Map Method — Example 3. 3 Simplify the Boolean function F(x, y, z) = (0, 2, 4, 5, 6) Figure 3. 6 F(x, y, z) = (0, 2, 4, 5, 6) = z' + xy' Fuw-Yi Yang 10

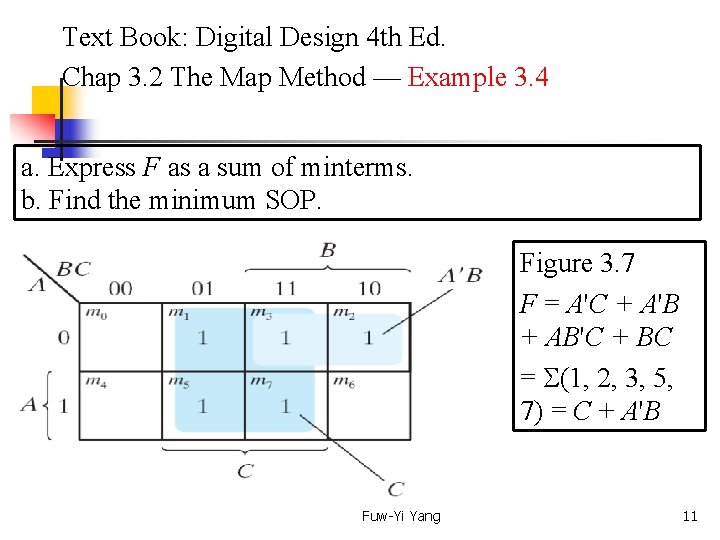
Text Book: Digital Design 4 th Ed. Chap 3. 2 The Map Method — Example 3. 4 a. Express F as a sum of minterms. b. Find the minimum SOP. Figure 3. 7 F = A'C + A'B + AB'C + BC = (1, 2, 3, 5, 7) = C + A'B Fuw-Yi Yang 11

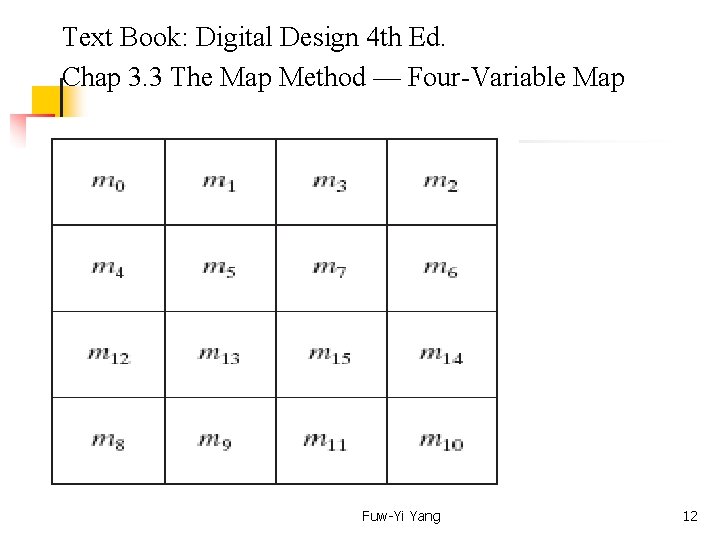
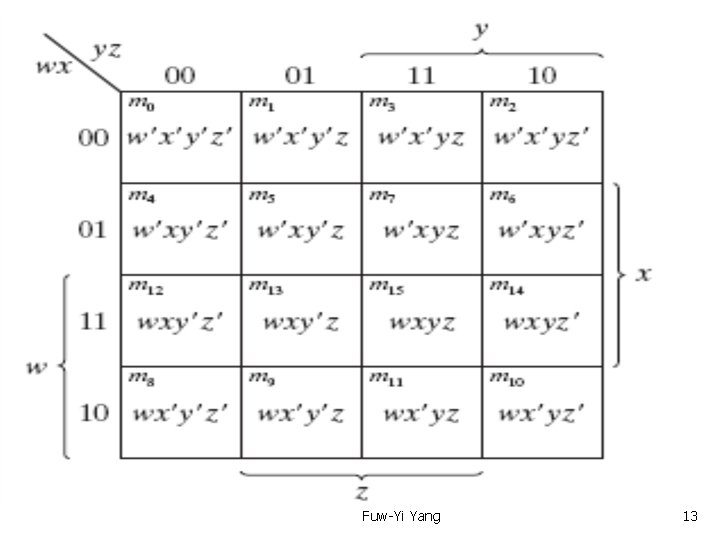
Text Book: Digital Design 4 th Ed. Chap 3. 3 The Map Method — Four-Variable Map Fuw-Yi Yang 12

Text Book: Digital Design 4 th Ed. Chap 3. 3 The Map Method — Four-Variable Map Fuw-Yi Yang 13

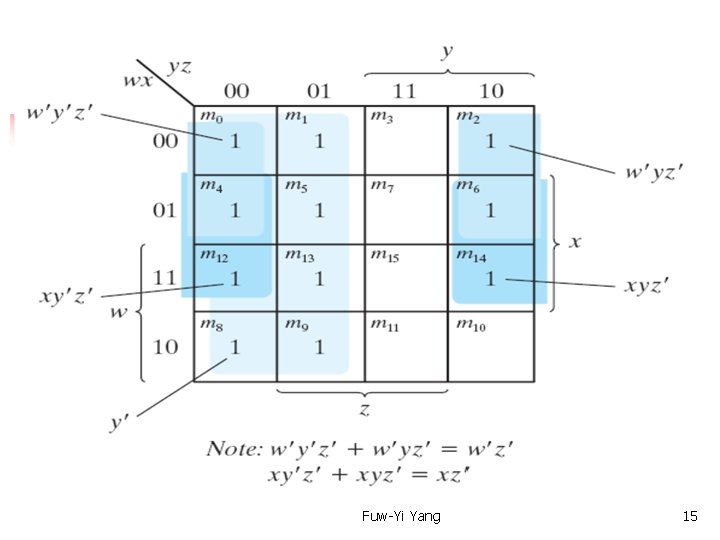
Text Book: Digital Design 4 th Ed. Chap 3. 3 The Map Method — Example 3. 5 Simplify F(w, x, y, z) = (0, 1, 2, 4, 5, 6, 8, 9, 12, 13, 14) Figure 3. 9 F = (0, 1, 2, 4, 5, 6, 8, 9, 12, 13, 14) = y'+ w' z'+ x z' Fuw-Yi Yang 14

Text Book: Digital Design 4 th Ed. Chap 3. 3 The Map Method — Example 3. 5 Fuw-Yi Yang 15

Text Book: Digital Design 4 th Ed. Chap 3. 3 The Map Method — Example 3. 6 Simplify F(A, B, C, D) = A'B'C' + B'CD' + A'BCD' + AB'C' Figure 3. 10 F = A'B'C' + B'CD' + A'BCD' + AB'C' = B'C' + B'D' + A'CD' see next page Fuw-Yi Yang 16

Text Book: Digital Design 4 th Ed. Chap 3. 3 The Map Method — Example 3. 6 Fuw-Yi Yang 17

Text Book: Digital Design 4 th Ed. Chap 3. 3 The Map Method — Prime implicants In choosing adjacent squares in a map, we must ensure that (1) all the minterms of the function are covered when we combine the squares, (2) the number of terms in the expression is minimized, and (3) there are no redundant terms (i. e. , minterms already covered by other terms). Fuw-Yi Yang 18

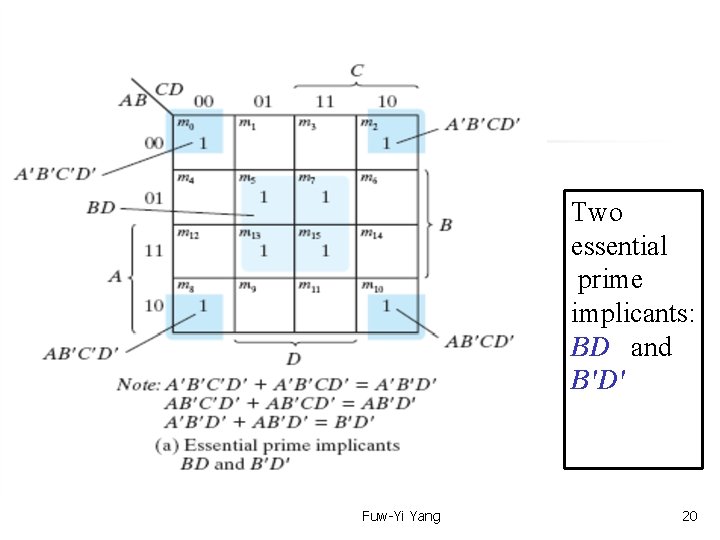
Text Book: Digital Design 4 th Ed. Chap 3. 3 The Map Method — Prime implicants A prime implicant is a product term obtained combining the maximum possible number of adjacent squares in the map. If a minterm in a square is covered by only one prime implicant, that prime implicant is said to be essential. Simplify F(A, B, C, D) = (0, 2, 3, 5, 7, 8, 9, 10, 11, 13, 15) See next pages Fuw-Yi Yang 19

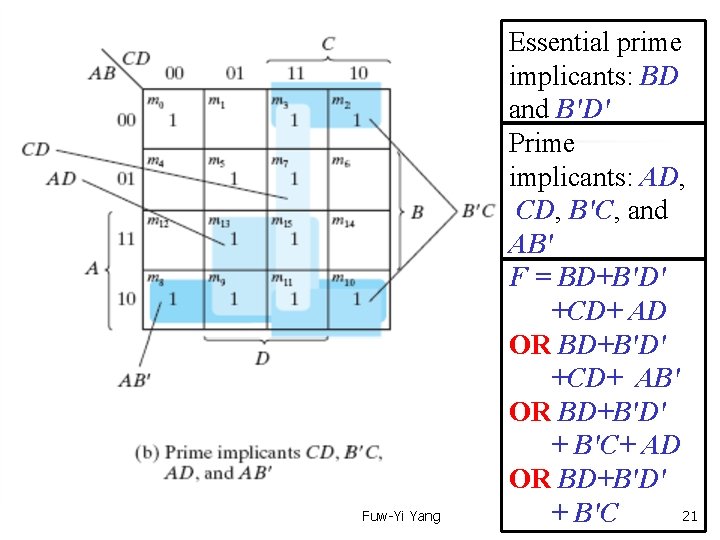
Text Book: Digital Design 4 th Ed. Chap 3. 3 The Map Method — prime Two essential prime implicants: BD and B'D' Fuw-Yi Yang 20

Fuw-Yi Yang Essential prime implicants: BD and B'D' Prime implicants: AD, CD, B'C, and AB' F = BD+B'D' +CD+ AD OR BD+B'D' +CD+ AB' OR BD+B'D' + B'C+ AD OR BD+B'D' 21 + B'C

Text Book: Digital Design 4 th Ed. Chap 3. 5 Product-of-Sums Simplification Example 3. 8 Simplify F(A, B, C, D) = (0, 1, 2, 5, 8, 9, 10) into a. sum-of-products form, taking the procedures as described previously, i. e. , group the squares marked by 1’s and combine them. b. product-of-sums form. Group the squares marked by 0’s and combine them, i. e. , we obtain F ' in the form of sum-of-product. Because of the generalized De. Morgan’s theorem, the product-of-sums form is also obtained. Procedures see next page Fuw-Yi Yang 22

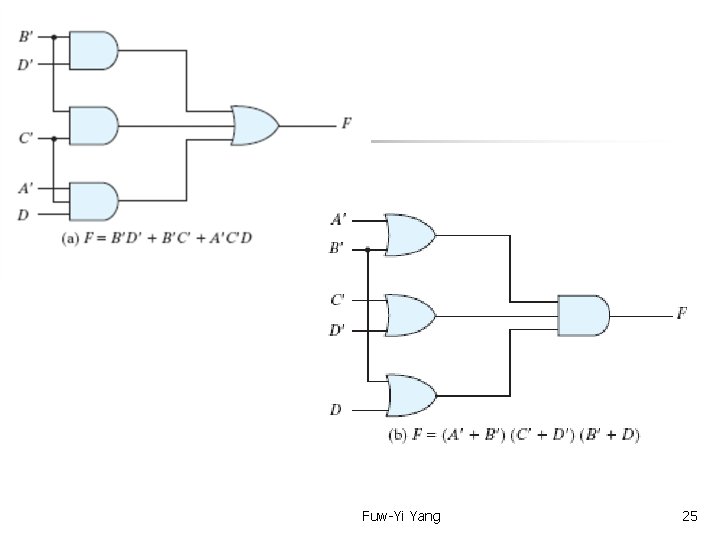
F=B'C' + B'D' + A'C'D' F' = AB + CD + BD' Applying De. Morgan’s theorem to F', F = (A' + B') + (C' + D') + (B' + D) Fuw-Yi Yang 23

F=B'C' + B'D' + A'C'D' F' = AB + CD + BD' Applying De. Morgan’s theorem to F', F = (A' + B') + (C' + D') + (B' + D) Implementation see next pages Fuw-Yi Yang 24

Fuw-Yi Yang 25

Text Book: Digital Design 4 th Ed. Chap 3. 5 Product-of-Sums Simplification a. sum-of-products form b. product-of-sums form These two forms can also obtain from truth table, see next page. Fuw-Yi Yang 26

Text Book: Digital Design 4 th Ed. Chap 3. 5 Product-of-Sums Simplification x 0 0 1 1 y 0 0 1 1 z 0 1 0 1 Table 3. 2 F 0 m 0, M 0 1 m 1, M 1 0 m 2, M 2 1 m 3, M 3 1 m 4, M 4 0 m 5, M 5 1 m 6, M 6 0 m 7, M 7 Fuw-Yi Yang F(x, y, z) = (1, 3, 4, 6) F(x, y, z) = (0, 2, 5, 7) = (x' + z') (x + z) See next page, note that we express F directly in the POS form. 27

F(x, y, z) = (1, 3, 4, 6) F'(x, y, z) = (0, 2, 5, 7) By De. Morgan’s Theorem F(x, y, z) = (0, 2, 5, 7) = (x' + z') (x + z) Fuw-Yi Yang 28

Text Book: Digital Design 4 th Ed. Chap 3. 6 Don’t Care Conditions Functions that have unspecified outputs for some input combinations are called incompletely specified functions. In most applications, we simply don’t care what value is assumed by the function for the unspecified minterms. For this reason, it is customary to call the unspecified minterms of a function don’t care conditions. These don’t care conditions can be used on a map to provide further simplification of a Boolean expression. Fuw-Yi Yang 29

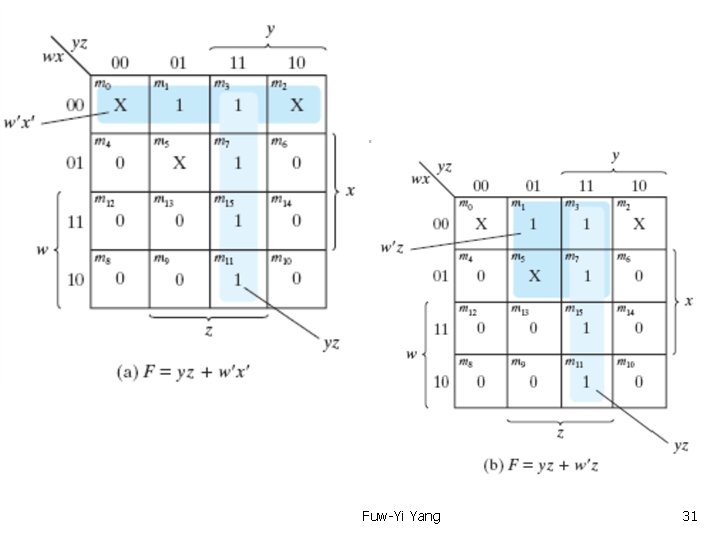
Text Book: Digital Design 4 th Ed. Chap 3. 6 Don’t Care Conditions Example 3. 9 Simplify the Boolean function F(w, x, y, z) = (1, 3, 7, 11, 15) which has the don’t care conditions d(w, x, y, z) = (0, 2, 5). Fuw-Yi Yang 30

Fuw-Yi Yang 31

Text Book: Digital Design 4 th Ed. Chap 3. 7 NAND and NOR Implementation Digital circuits are frequently constructed with NAND or NOR gates rather than with AND and OR gates. NAND and NOR gates are easier to fabricate with electronic components and are the basic gates used in all IC digital logic families. Because of the prominence of NAND and NOR gates in the design of digital circuits, rules and procedures have been developed for the conversion from Boolean functions given in terms of AND, OR, and NOT into equivalent NAND and NOR logic diagrams. Fuw-Yi Yang 32

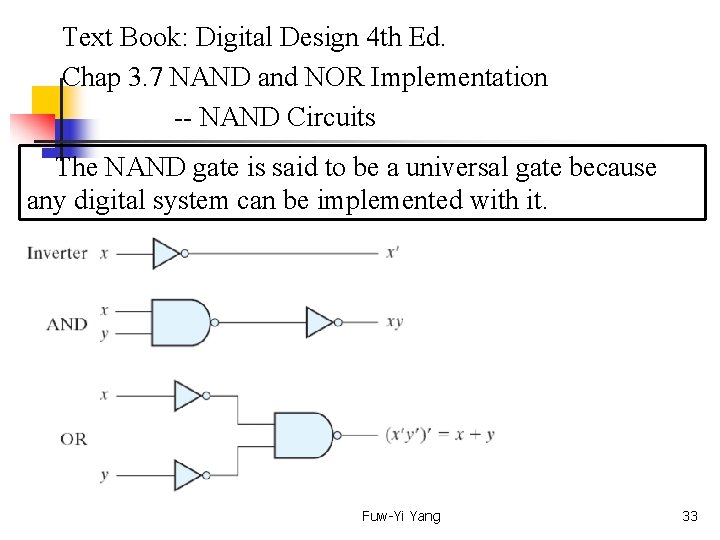
Text Book: Digital Design 4 th Ed. Chap 3. 7 NAND and NOR Implementation -- NAND Circuits The NAND gate is said to be a universal gate because any digital system can be implemented with it. Fuw-Yi Yang 33

Text Book: Digital Design 4 th Ed. Chap 3. 7 NAND and NOR Implementation -- NAND Circuits A convenient way to implement a Boolean function with NAND gates is to obtain the simplified Boolean function in terms of Boolean operators and then convert the function to NAND logic. The conversion of an algebraic expression from AND, OR, and complement to NAND can be done by simple circuit manipulation technique that change AND-OR diagrams to NAND diagrams. (minterms) Fuw-Yi Yang 34

Text Book: Digital Design 4 th Ed. Chap 3. 7 NAND and NOR Implementation -- NAND Circuits Two equivalent graphic symbols for the NAND gate are shown below. It is convenient to use them in converting AND, OR, and NOT expressions into NAND expressions. See next page. Fuw-Yi Yang 35

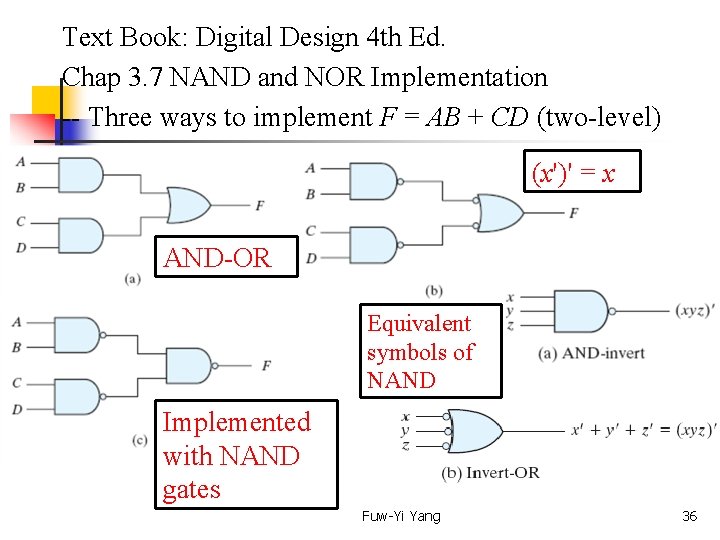
Text Book: Digital Design 4 th Ed. Chap 3. 7 NAND and NOR Implementation -- Three ways to implement F = AB + CD (two-level) (x')' = x AND-OR Equivalent symbols of NAND Implemented with NAND gates Fuw-Yi Yang 36

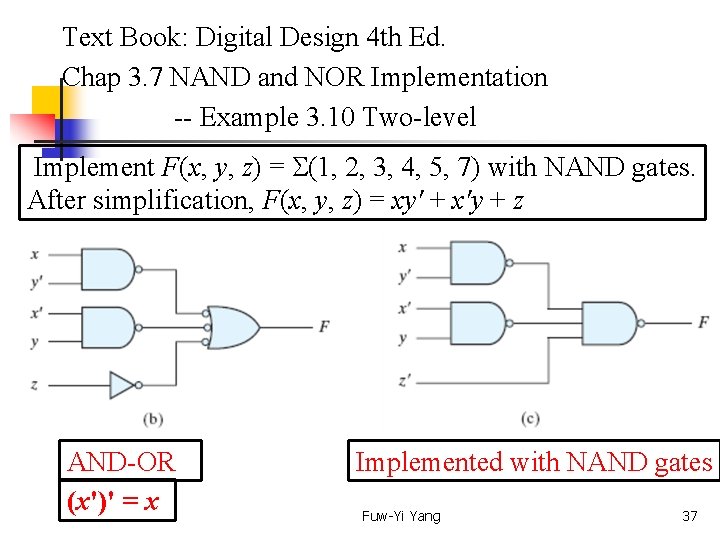
Text Book: Digital Design 4 th Ed. Chap 3. 7 NAND and NOR Implementation -- Example 3. 10 Two-level Implement F(x, y, z) = (1, 2, 3, 4, 5, 7) with NAND gates. After simplification, F(x, y, z) = xy' + x'y + z AND-OR (x')' = x Implemented with NAND gates Fuw-Yi Yang 37

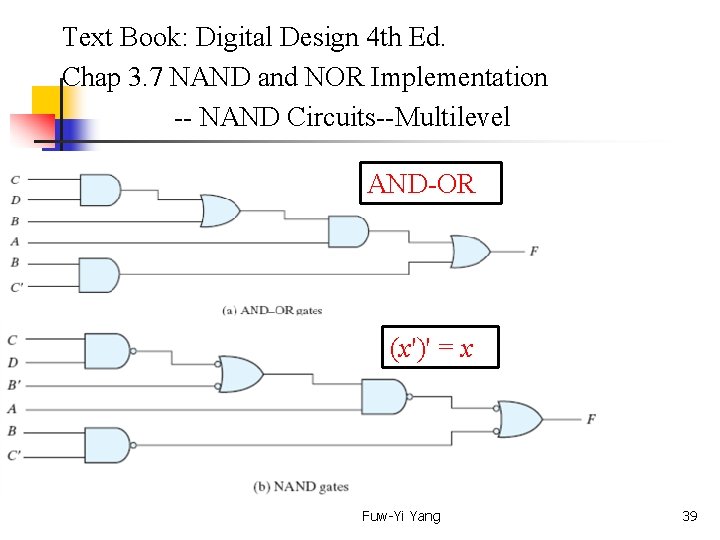
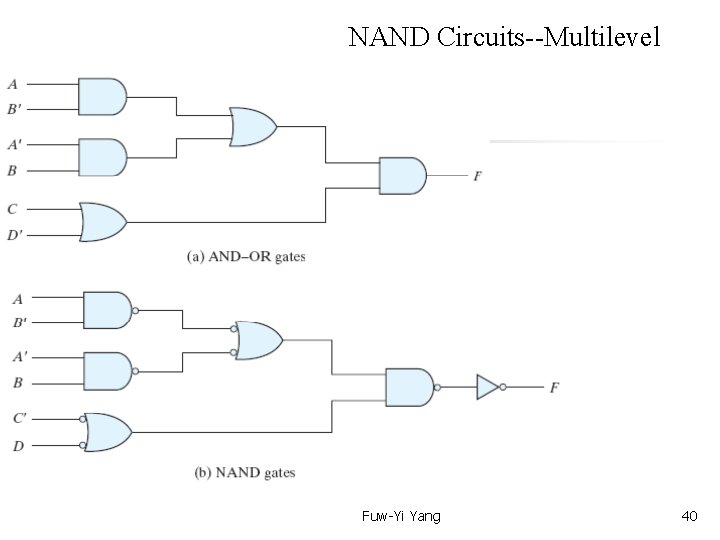
Text Book: Digital Design 4 th Ed. Chap 3. 7 NAND and NOR Implementation -- NAND Circuits--Multilevel There are occasions, however, when the design of digital systems results in gating structures with three or more levels. The most common procedure in the design of multilevel circuits is to express the Boolean function in terms of AND, OR, and complement operations. The function can then be implemented with AND and OR gares. After that, if necessary, it can be converted into an all-NAND circuit. See next page. Fuw-Yi Yang 38

Text Book: Digital Design 4 th Ed. Chap 3. 7 NAND and NOR Implementation -- NAND Circuits--Multilevel AND-OR (x')' = x Fuw-Yi Yang 39

NAND Circuits--Multilevel Fuw-Yi Yang 40

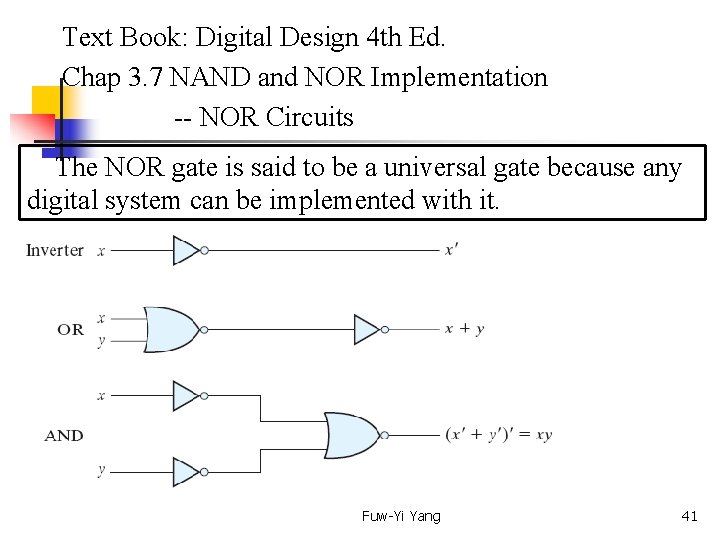
Text Book: Digital Design 4 th Ed. Chap 3. 7 NAND and NOR Implementation -- NOR Circuits The NOR gate is said to be a universal gate because any digital system can be implemented with it. Fuw-Yi Yang 41

Text Book: Digital Design 4 th Ed. Chap 3. 7 NAND and NOR Implementation -- NOR Circuits A convenient way to implement a Boolean function with NOR gates is to obtain the simplified Boolean function in terms of Boolean operators and then convert the function to NOR logic. The conversion of an algebraic expression from AND, OR, and complement to NOR can be done by simple circuit manipulation technique that change OR-AND diagrams to NOR diagrams. (maxterms) Fuw-Yi Yang 42

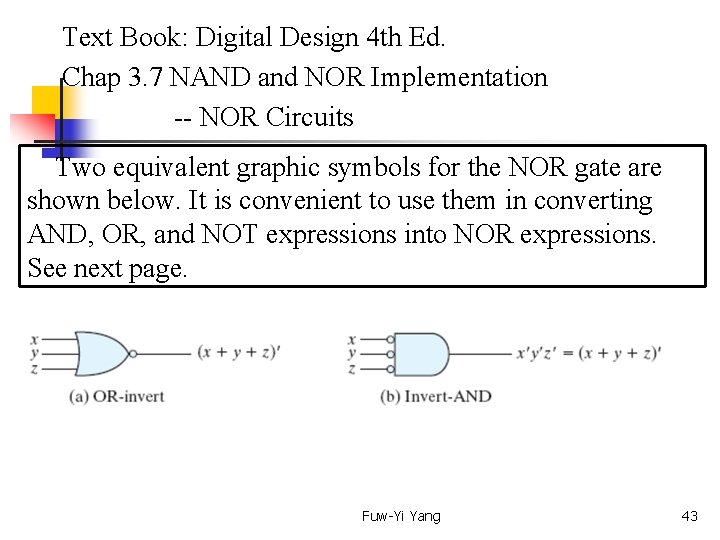
Text Book: Digital Design 4 th Ed. Chap 3. 7 NAND and NOR Implementation -- NOR Circuits Two equivalent graphic symbols for the NOR gate are shown below. It is convenient to use them in converting AND, OR, and NOT expressions into NOR expressions. See next page. Fuw-Yi Yang 43

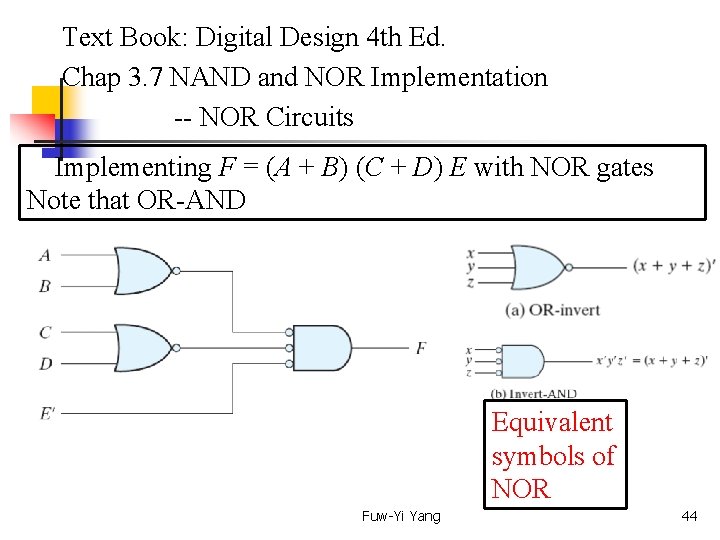
Text Book: Digital Design 4 th Ed. Chap 3. 7 NAND and NOR Implementation -- NOR Circuits Implementing F = (A + B) (C + D) E with NOR gates Note that OR-AND Equivalent symbols of NOR Fuw-Yi Yang 44

Text Book: Digital Design 4 th Ed. Chap 3. 7 NAND and NOR Implementation -- NOR Circuits Implementing F = (AB' + A'B) (C + D') with NOR gates Note that OR-AND Equivalent symbols of NOR Fuw-Yi Yang 45

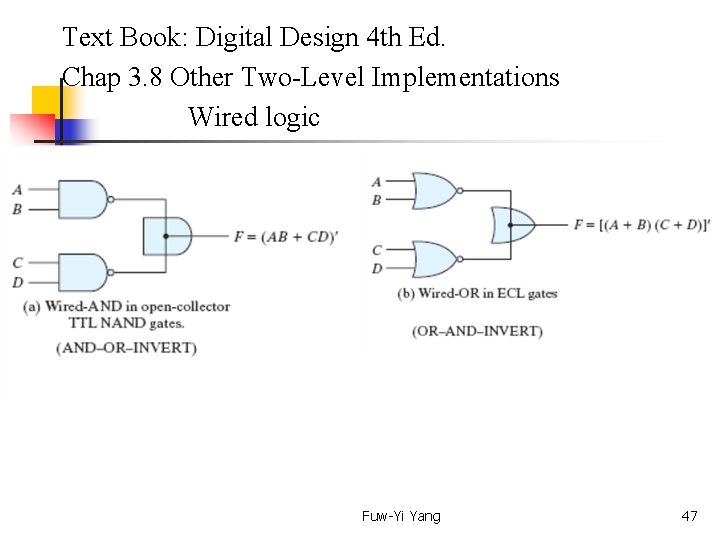
Text Book: Digital Design 4 th Ed. Chap 3. 8 Other Two-Level Implementations The types of gates most often found in integrated circuits are NAND and NOR gates. For this reason, NAND and NOR logic implementations are the most important from a practical point of view. Some NAND and NOR gates allow the possibility of a wire connection between the outputs of two gates to provide a specific logic function. This type of logic is called wired logic. See next pages Fuw-Yi Yang 46

Text Book: Digital Design 4 th Ed. Chap 3. 8 Other Two-Level Implementations Wired logic Fuw-Yi Yang 47

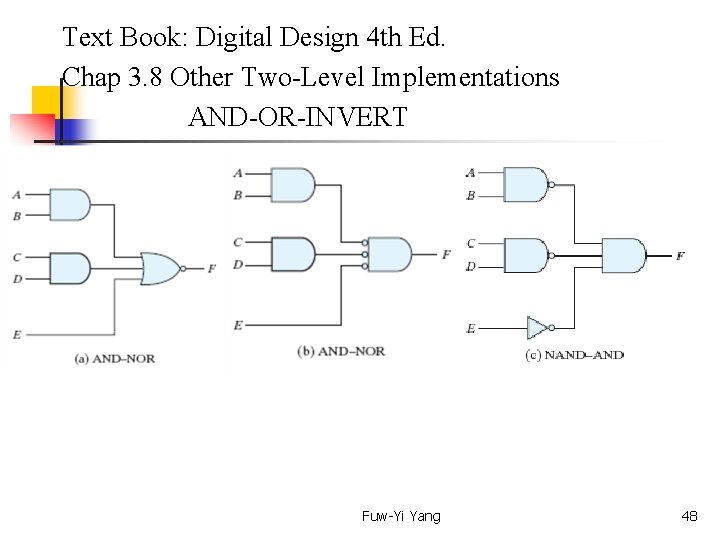
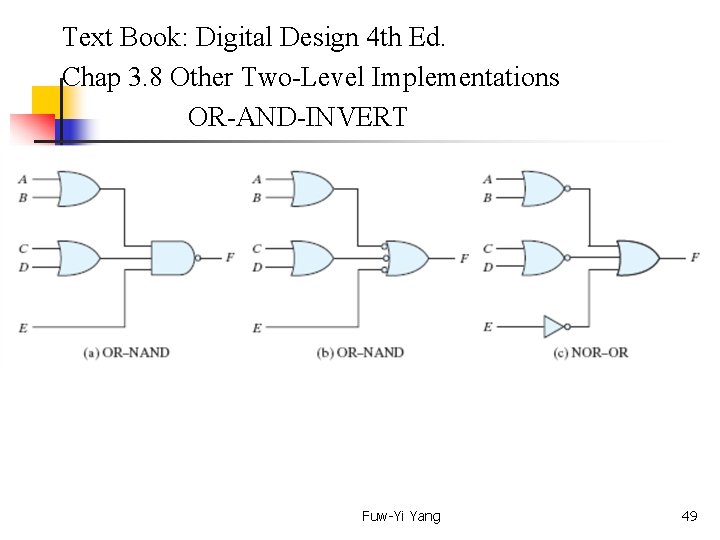
Text Book: Digital Design 4 th Ed. Chap 3. 8 Other Two-Level Implementations AND-OR-INVERT Fuw-Yi Yang 48

Text Book: Digital Design 4 th Ed. Chap 3. 8 Other Two-Level Implementations OR-AND-INVERT Fuw-Yi Yang 49

Text Book: Digital Design 4 th Ed. Chap 3. 8 Other Two-Level Implementations Fuw-Yi Yang 50

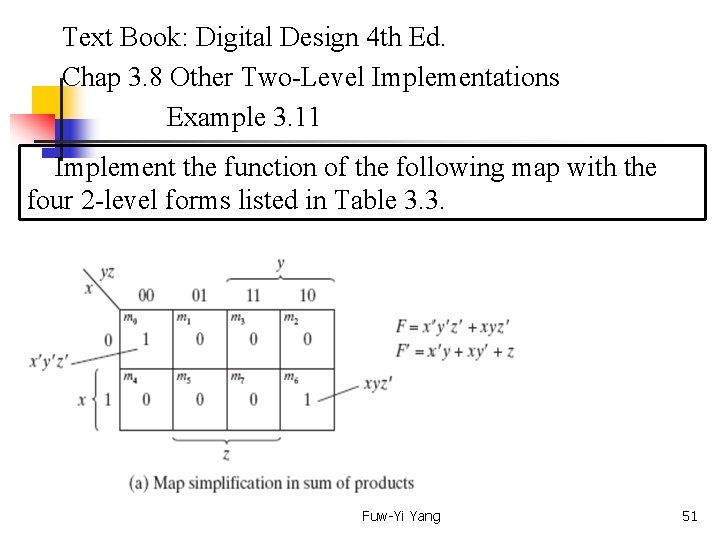
Text Book: Digital Design 4 th Ed. Chap 3. 8 Other Two-Level Implementations Example 3. 11 Implement the function of the following map with the four 2 -level forms listed in Table 3. 3. Fuw-Yi Yang 51

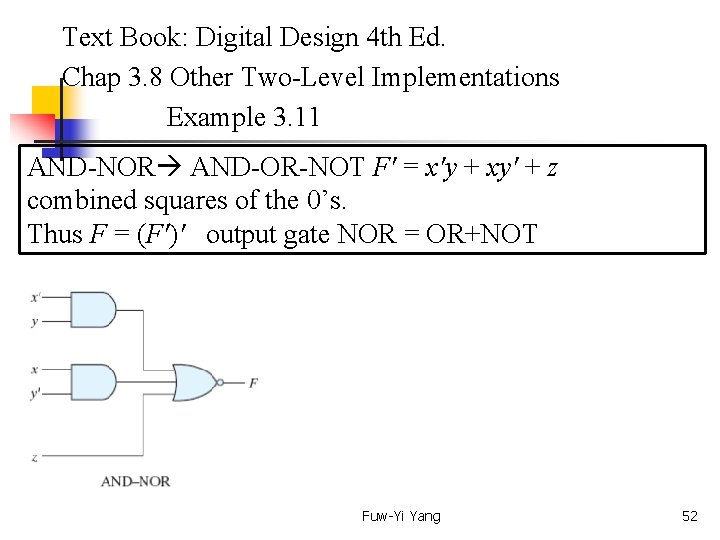
Text Book: Digital Design 4 th Ed. Chap 3. 8 Other Two-Level Implementations Example 3. 11 AND-NOR AND-OR-NOT F' = x'y + xy' + z combined squares of the 0’s. Thus F = (F')' output gate NOR = OR+NOT Fuw-Yi Yang 52

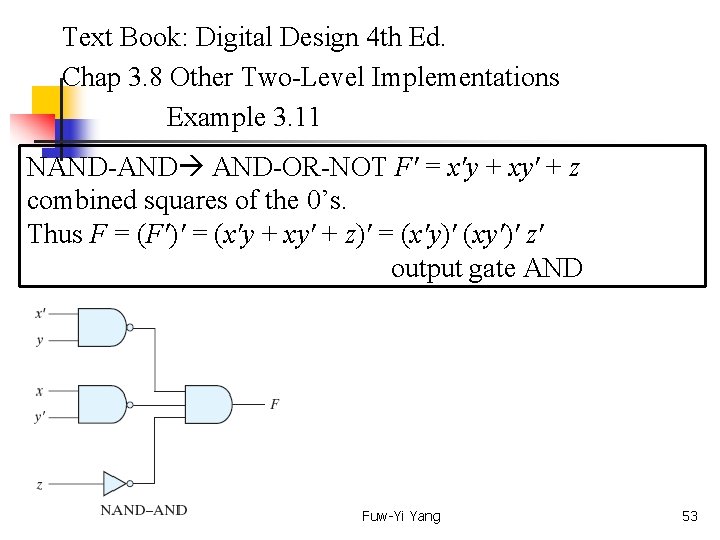
Text Book: Digital Design 4 th Ed. Chap 3. 8 Other Two-Level Implementations Example 3. 11 NAND-AND AND-OR-NOT F' = x'y + xy' + z combined squares of the 0’s. Thus F = (F')' = (x'y + xy' + z)' = (x'y)' (xy')' z' output gate AND Fuw-Yi Yang 53

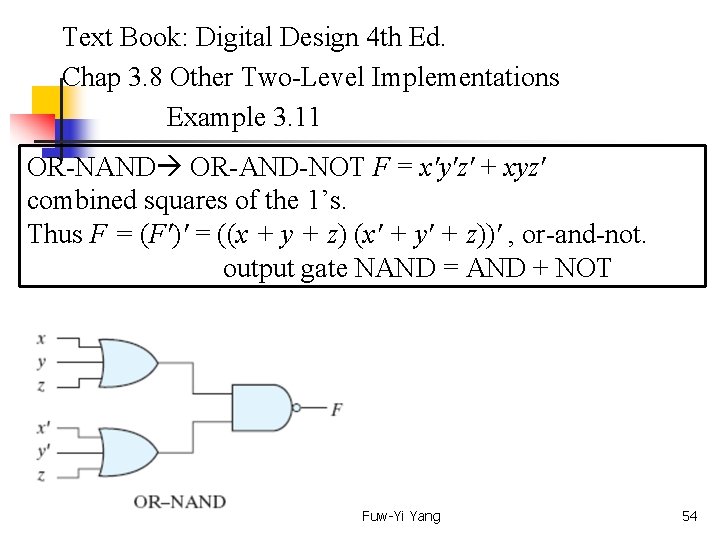
Text Book: Digital Design 4 th Ed. Chap 3. 8 Other Two-Level Implementations Example 3. 11 OR-NAND OR-AND-NOT F = x'y'z' + xyz' combined squares of the 1’s. Thus F = (F')' = ((x + y + z) (x' + y' + z))' , or-and-not. output gate NAND = AND + NOT Fuw-Yi Yang 54

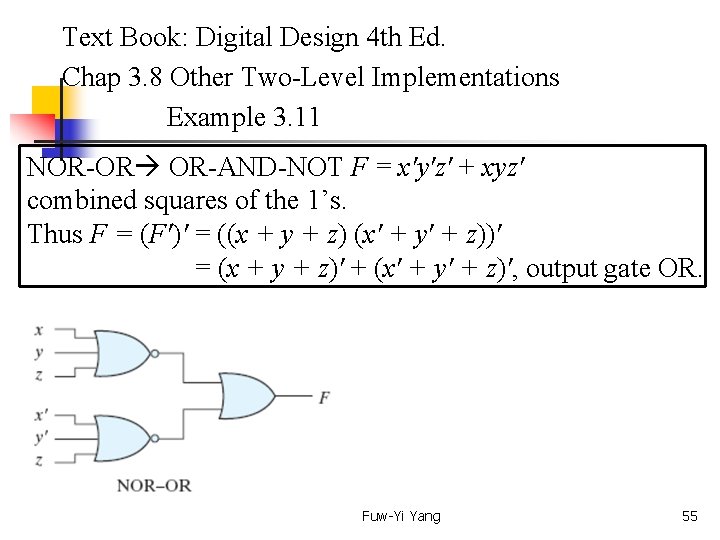
Text Book: Digital Design 4 th Ed. Chap 3. 8 Other Two-Level Implementations Example 3. 11 NOR-OR OR-AND-NOT F = x'y'z' + xyz' combined squares of the 1’s. Thus F = (F')' = ((x + y + z) (x' + y' + z))' = (x + y + z)' + (x' + y' + z)', output gate OR. Fuw-Yi Yang 55

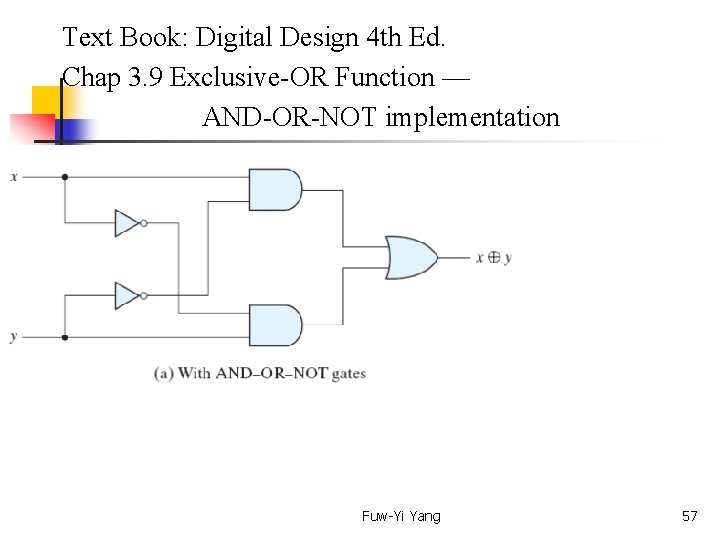
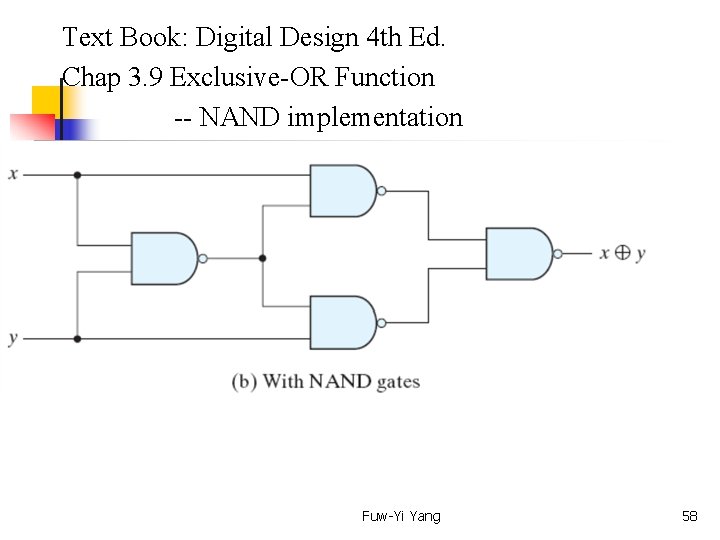
Text Book: Digital Design 4 th Ed. Chap 3. 9 Exclusive-OR Function The exclusive-OR (XOR), denoted by the symbol , is a logical operation that performs the following Boolean operation: x y = x'y + xy'. It can be shown that the exclusive-OR operation is both commutative and associative; that is, x y = y x and (x y) z = x (y z) = x y z. For implementation, see next pages. Fuw-Yi Yang 56

Text Book: Digital Design 4 th Ed. Chap 3. 9 Exclusive-OR Function — AND-OR-NOT implementation Fuw-Yi Yang 57

Text Book: Digital Design 4 th Ed. Chap 3. 9 Exclusive-OR Function -- NAND implementation Fuw-Yi Yang 58

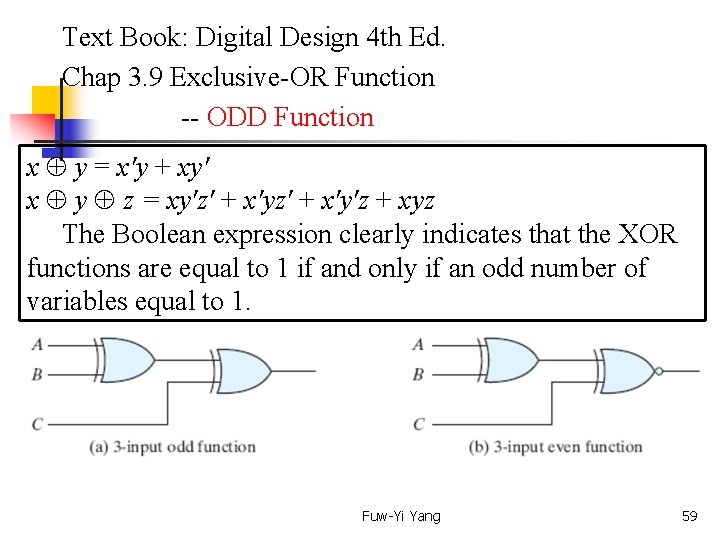
Text Book: Digital Design 4 th Ed. Chap 3. 9 Exclusive-OR Function -- ODD Function x y = x'y + xy' x y z = xy'z' + x'y'z + xyz The Boolean expression clearly indicates that the XOR functions are equal to 1 if and only if an odd number of variables equal to 1. Fuw-Yi Yang 59

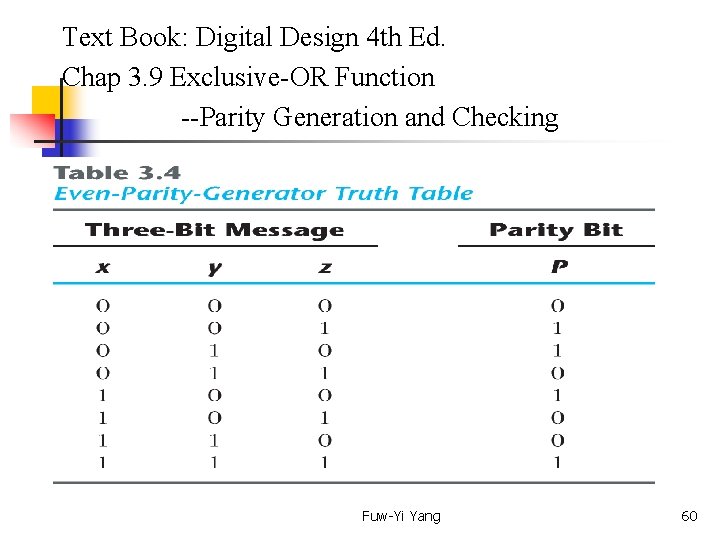
Text Book: Digital Design 4 th Ed. Chap 3. 9 Exclusive-OR Function --Parity Generation and Checking Fuw-Yi Yang 60

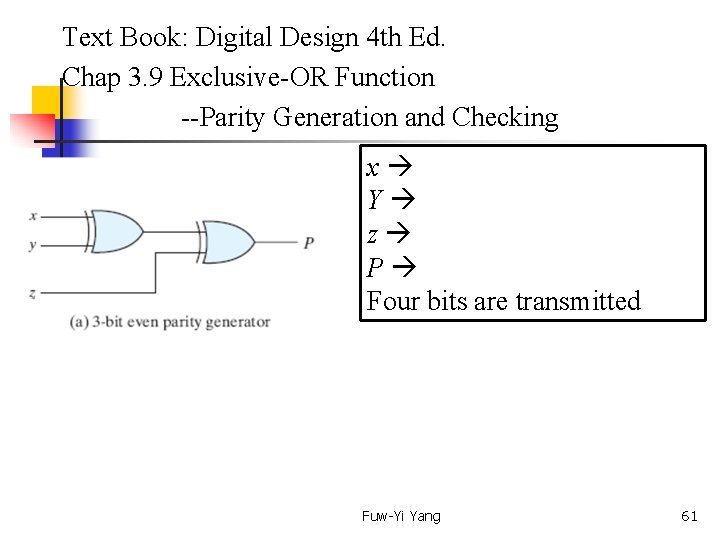
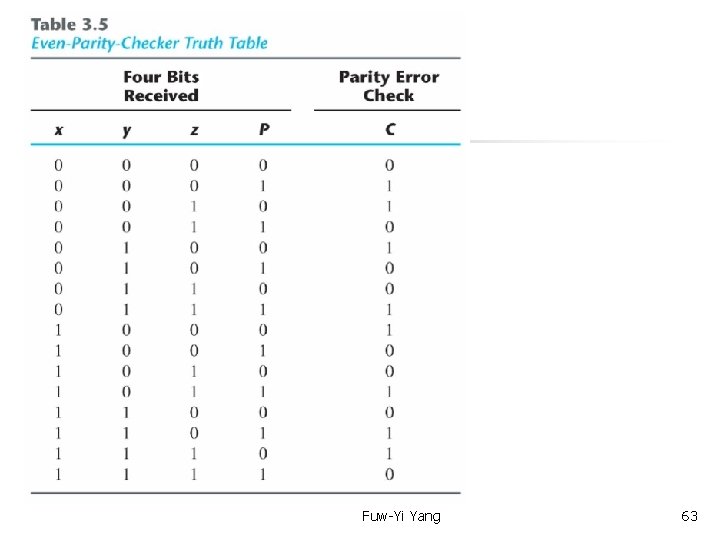
Text Book: Digital Design 4 th Ed. Chap 3. 9 Exclusive-OR Function --Parity Generation and Checking x Y z P Four bits are transmitted Fuw-Yi Yang 61

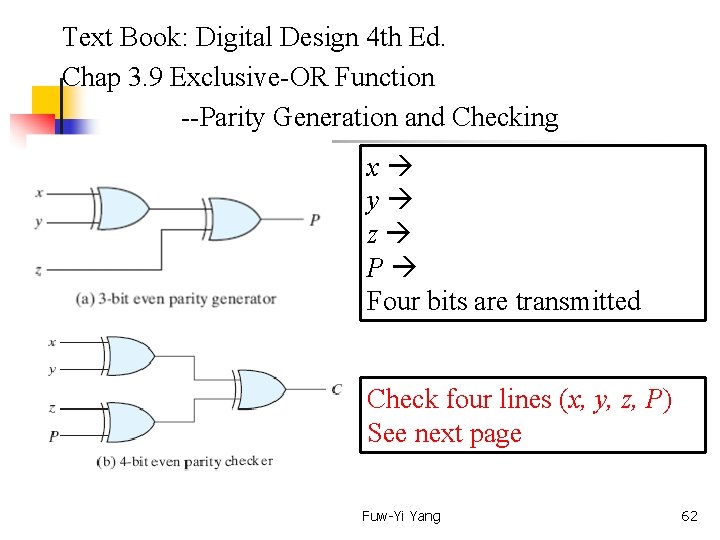
Text Book: Digital Design 4 th Ed. Chap 3. 9 Exclusive-OR Function --Parity Generation and Checking x y z P Four bits are transmitted Check four lines (x, y, z, P) See next page Fuw-Yi Yang 62

Fuw-Yi Yang 63

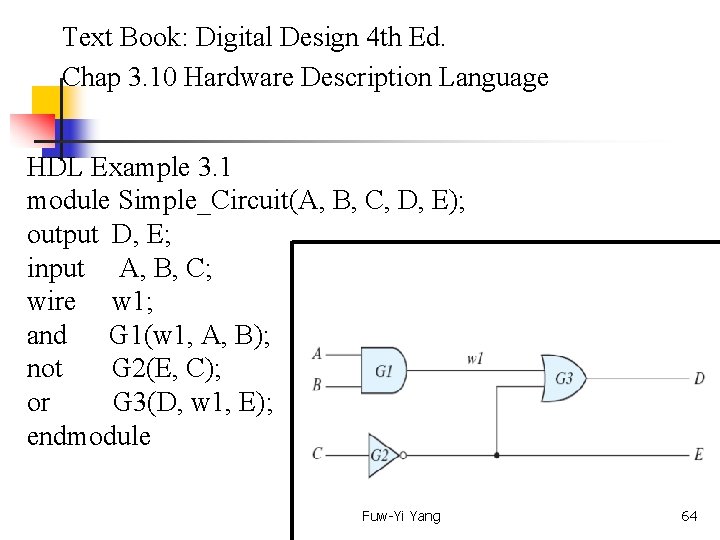
Text Book: Digital Design 4 th Ed. Chap 3. 10 Hardware Description Language HDL Example 3. 1 module Simple_Circuit(A, B, C, D, E); output D, E; input A, B, C; wire w 1; and G 1(w 1, A, B); not G 2(E, C); or G 3(D, w 1, E); endmodule Fuw-Yi Yang 64