Digital Signature Integrity Authenticity Unforgeability Nonrepudiation Irreusability Conventional

Digital Signature Integrity Authenticity Unforgeability Non-repudiation Irreusability

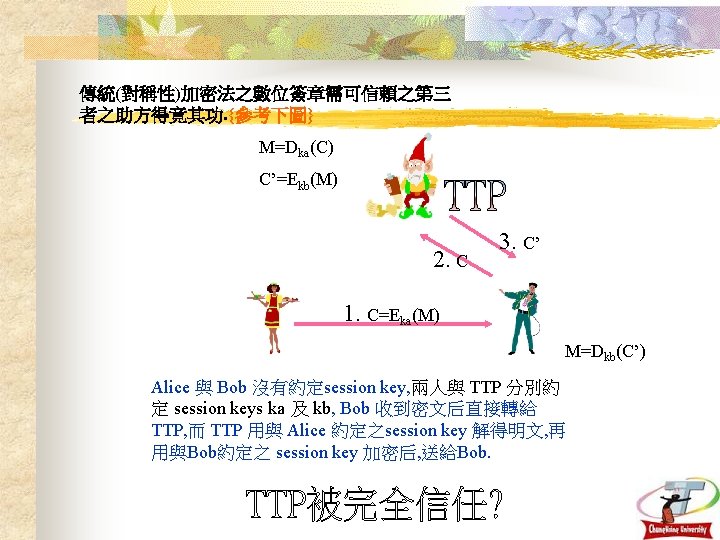
Conventional signature VS. Digital signature 1. A signature is physically part of the document being signed. A digital signature is not attached physically to the message that is signed. 2. A signature is verified by comparing it to authentic signatures. Digital signatures can be verified using a publicly known verification algorithm. 3. A copy of a signed paper document can usually be distinguished from an original. A “copy” of a signed digital message is identical to the original. 2

Digital Signatures based on DLP: El. Gamal signature scheme Schnorr signature scheme Digital Signature Algorithm (DSA) DSA He and Kiesler’s Kiesler signature scheme 3

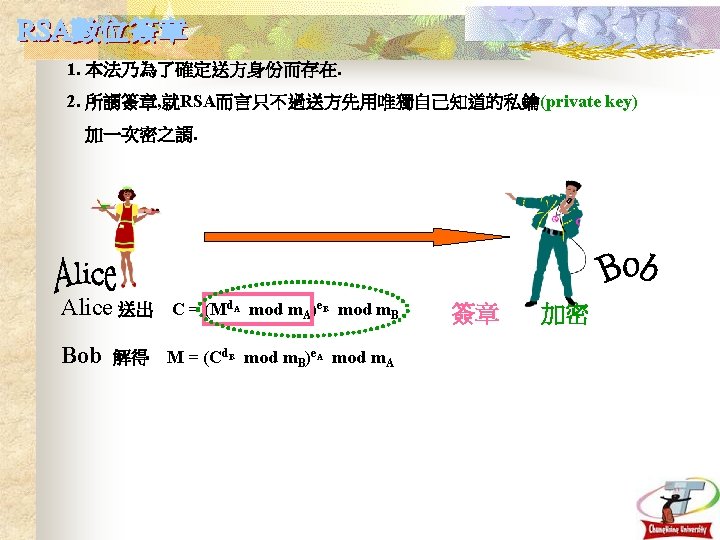
Digital Signatures based on FAC( factoring problem): RSA signature scheme Rabin digital signature scheme OSS( Ong, Schnorr, & Shamir) signature scheme Modified OSS signature scheme 4

For a (finite) multiplicative group G, define the order of an element g G to be the smallest positive integer T such that g. T = 1 = g 0 in Zp. 若 g G 之 order 是 P-1 {P為質數且集合 G 定義於ZP}, 則 g 稱為 mod P 之原根. //當 g 為 mod P 之primitive root, 由 g 所產生之序列(sequence) 具有最大週期, 因此安全上較佳. // 理論上可證: 對所有質數 P, 其原根必定 存在. 若 g 為 mod P 之 primitive root, 且 a 與 P-1 互質, 則 g a mod P 必為 mod P之原根. mod P 之原根個數等於 (P-1) ----- Euler Totient Function. 例: 若 p=10, 則 (10)={1, 3, 7, 9}, 因此 p=11 時共有 4 個原根; 即 [ 因我們已知 2 是 mod 11 之原根, 故] 21 = 2 23 = 8 27 = 7 29 = 6 2, 8, 7, 6 均是 mod 11 之原根 11

多數數位簽章法均有類似的攻擊法存在, 若能使用 one-way hash function 合併之, 則可高枕無憂矣. 請參照後續之介紹. One-way: (1) hash fun 對任意長度的明文, 產生固定長度的密文. (2) hash fun對任意明文M, 藉 HW/SW 易求得 h(M). 防攻擊 : (3) 對任意hash fun 值 x, 計算上不可能藉 x=h(M)求M. (4) 對任一明文M 1, 要找另一明文 M 2 使得 h(M 1 ) =h(M 2) 在計算上不可行. (5) 要找任一對 (M 1 , M 2)明文對, 使得h(M 1 ) =h(M 2) 在計算上不可行. Unfortunately, although there are many functions that are believed to be one-way, there currently do not exist functions that can be proved to be one-way. Zm is defined to be the set {0, 1, . . . , m-1}, equipped with two operators, + and *. Addition and multiplication in Zm work exactly like real addition and multiplication, except that the results are reduced modulo m. 相信 f(x) = xb mod n, gcd(x, n)=1 是 one-way function. For a (finite) multiplicative group G, define the order of an element g G to be the smallest positive integer t such that gt = 1 in Zp. 12

14

15

16

{CRYPTO’ 89} 1. 2. 3. 4. 5. 大質數 P 及 q 滿足 q|P-1, q 2160 及 P 2512 g Zp 且滿足 gq = 1 mod P, g 1 h 為 one-way hash fun. Signer Bob 之私鑰 x , 1 < x < q Bob 之公鑰 y = gx mod P. 1. Bob 任選一整數 k , 1 < k < q, 並求出 r = g k mod P 2. 求出 e = h(r, M) 3. 求出 s = k - x e mod q, (e, s) 即 Bob 對 M 之簽署文. 驗證者(Verifier) Alice 求出: 1. Let r’ = gs ye mod P ? 2. 檢查 h(r’ , M) = e r’ = gsye = gk-xegxe = gk = r h(r’ , M) = h(r , M) = e r = gk = gs + xe = gs gxe = gsye Meanwhile since q|P-1, the exponential part should be computed with mod q for the size of computations. (mod P) 21

23

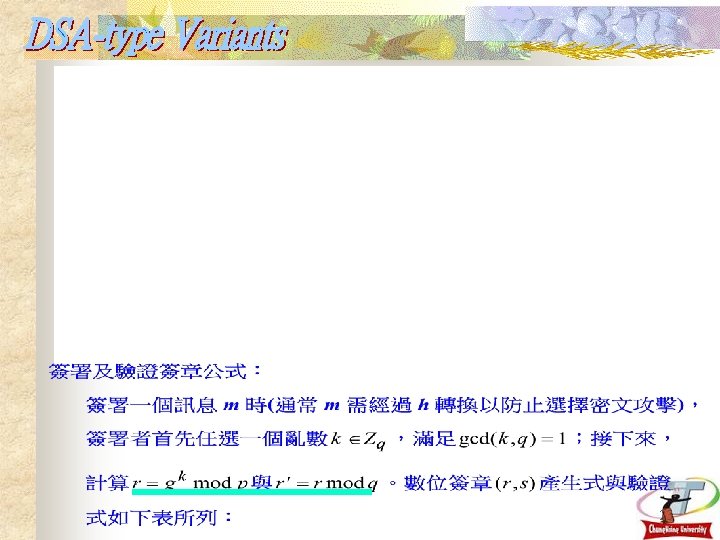
前提如 DSA-type form, 然而 此處 g , {r, s} is the digital signature of message m, k and x are secrets of the signer. In El. Gamal original scheme, there are five parameters {r, s, m, k, x} in the signature signing equation. Although additional generalization and variants can generate more than 13, 000 variants, but these 18 variants are the most efficient variants since each of them permutes these five parameters directly. 1. mx = rk + s mod p-1 ym = r r s mod p 左 = ym = (gx)m = gxm 右 = r r s = (gk)r gs = gkr+s = gxm = 左 2. mx = sk + r mod p-1 ym = r s r mod p 驗證第一種: mx 3. rx = mk + s mod p-1 yr = r m s mod p 25

4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. rx = sk + m mod p-1 sx = rk + m mod p-1 sx = mk + r mod p-1 rmx = k + s mod p-1 x = mrk + s mod p-1 sx = k + mr mod p-1 x = sk + rm mod p-1 rmx = sk + 1 mod p-1 sx = rmk + 1 mod p-1 (r+m)x = k + s mod p-1 x = (m+r)k + s mod p-1 sx = k + (m+r) mod p-1 x = sk + (r+m) mod p-1 (r+m)x = sk + 1 mod p-1 sx = (r+m)k + 1 mod p-1 yr = r m s mod p ys = r r m mod p ys = r mod p yr m = r s mod p y = r mr s mod p ys = r mr mod p y = r s r m mod p yr m = r s mod p ys = r mr mod p yr+m = r s mod p y = r m+r s mod p ys = r m+r mod p y = r s m+r mod p yr+m = r s mod p ys = r m+r mod p 26

( D. Chaum & H. van Antwerpen at CRYPTO’ 89) Known facts: a large prime P, and a primitive element g, are made public, and used by a group of signers. Alice has a private key, x, and a public key , gx. To sign a message, Alice computes z = Mx. That’s all she needs to do. Verification is a little more complicated: (B 要 A 印證 z 是她簽署的) (1) Bob chooses two random numbers, a and b, both less then P, and sends Alice: c = z a(gx)b (mod P) (2) Alice computes x -1 (mod P-1), and sends Bob: d = cx -1 (mod P) (3) Bob confirms that d Magb (mod P) (此式子可馬上導證; 讀者自己試試看) If it is, he accepts the signature as genuine. 1. 此簽章法無法將明文M還原. 2. 除了signer Alice 外, 無人知道其私鑰 x , 故不能否認簽署之事實. 3. 下一方法是D. Chaum 在EUROCRYP 90所提之zero-knowledge undeniable signature. 27

( D. Chaum at EUROCRYPTO’ 90) Known facts: a large prime P, and a primitive element g, are made public, and used by a group of signers. Alice has a private key, x, and a public key , gx. To sign a message, Alice computes z = Mx. ① To verify a signature: (B 要 A 印證 [with Zero-Knowledge] z 是她簽署的) (1) Bob chooses two random numbers, a and b, both less then P, and sends Alice: c = Magb (mod P) ② (2) Alice chooses a random number, q, less than P, and computes and sends to Bob: s 1 = cg q ① s 2 = (cg q )x (mod P)③ ② ③ (3) Bob sends Alice a and b, so that Alice can confirm that Bob did not cheat in step (1). (4) Alice sends Bob q, so that Bob can use Mx and reconstructs s 1 and s 2. If s 1 = cg q s 2 = (gx)b+q za (此式子可馬上導證; 讀者自己試試看) If they are, he accepts the signature as genuine. 28

d Magb (mod P) ? (此式子[指page 21 之方法]可馬上導證): d = cx -1 = (za (gx)b) x -1 = za/x (g 1)b = Mx(a/x) gb = Magb (mod P) s 2 = (gx)b+q za ? (此式子[指page 22 之方法]可馬上導證) s 2 = (cg q )x = c x g xq = (Magb )x g xq = Maxgbx g xq = g xq+xb. Max = (gx)b+q za 29

30

31

Let P be a large prime number, Q be a prime factor of P-1, and G be a primitive element to mod P. { all these three are known to public}, Now, the signer holds SK [1, Q-1] as secret key and PK=GSK mod P as public key , plaintext M [1, P-1] and a random number r [1, Q-1]. SG 1 = M * G r mod P SG 2 = SK * SG 1 + r mod Q 任何人可用下列方式驗證送方身份並且可 recover message M : M ? G -SG 2 * PK SG 1 * SG 1 mod P G -SK*SG 1 -r * G SK * SG 1 * M * G r M * G -SK*SG 1 -r + SK * SG 1 +r mod P 1994年 Carmenisch, Piveteau & Stadler(CPS) 利用上述精神提出一盲簽章法 32

33

34

系統參數: signer holds SK [1, Q-1] as secret key and PK=GSK mod P as public key , and a random number r [1, Q-1]. signer 1 requester K = G r mod P, r [1, Q-1] 任選兩亂數(盲因子) , [1, Q-1] 算 SG 1 = M * G * K mod P C = SG 1 * -1 mod Q 算 SG 2 = SGC * + (4) M ? G -SG 2 * PK SG 1 = (G -SGC * - SGC = C * SK + r mod Q 3 (5) mod Q * SG 1 mod P ) * (GSK * SG 1) * (M * G * K ) mod P = (G -(C *SK + r)* = (G -SG 1*SK -r * = 2 - ) * (GSK * SG 1) * (M * G * G M * G -SG 1*SK -r * - +SG 1*SK +r * + mod P. r * ) mod P 36