Digital Signals and Systems 1 Digital Signals Functional

Digital Signals and Systems 1

Digital Signals Functional representation Tabular representation Sequence representation (bold or arrow for origin n=0) 2

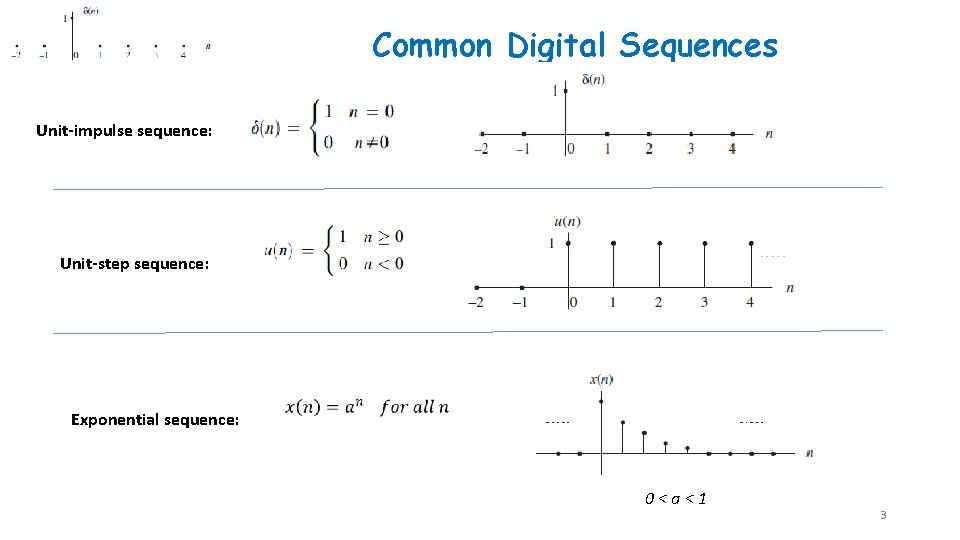
Common Digital Sequences Unit-impulse sequence: Unit-step sequence: Exponential sequence: 0<a<1 3

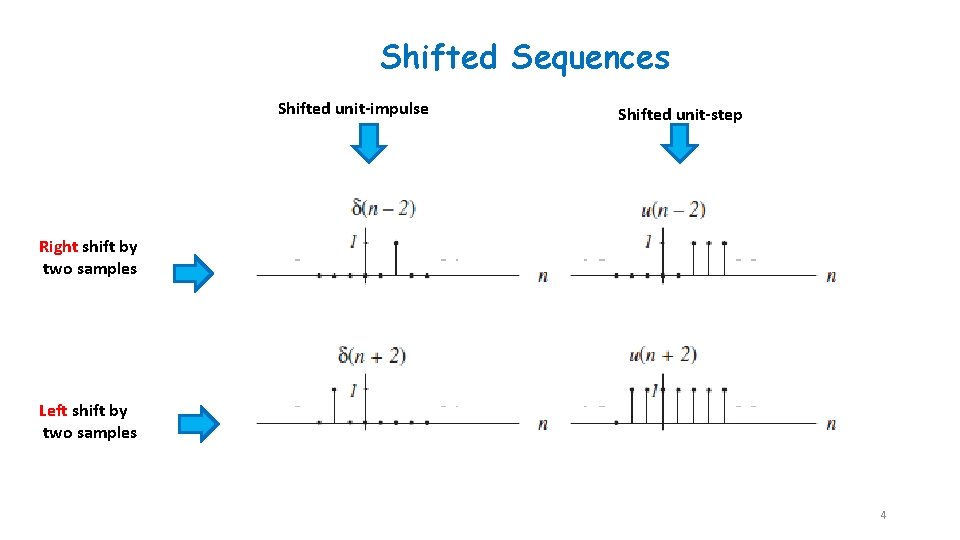
Shifted Sequences Shifted unit-impulse Shifted unit-step Right shift by two samples Left shift by two samples 4

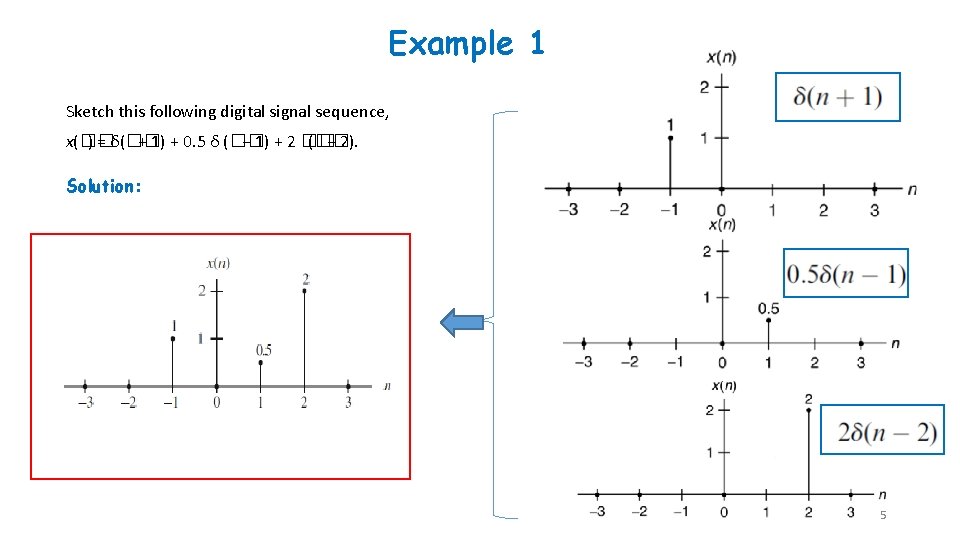
Example 1 Sketch this following digital signal sequence, x(�� ) = δ(�� + 1) + 0. 5 δ (�� − 1) + 2 �� (�� − 2). Solution: 5

Generation of Digital Signals x(n): digital signal x(t): analog signal Also 6

Example 2 Convert analog signal x(t) into digital signal x(n), when sampling period is 125 microsecond, also plot sample values. Solution: The first five sample values: Plot of the digital sequence: 7

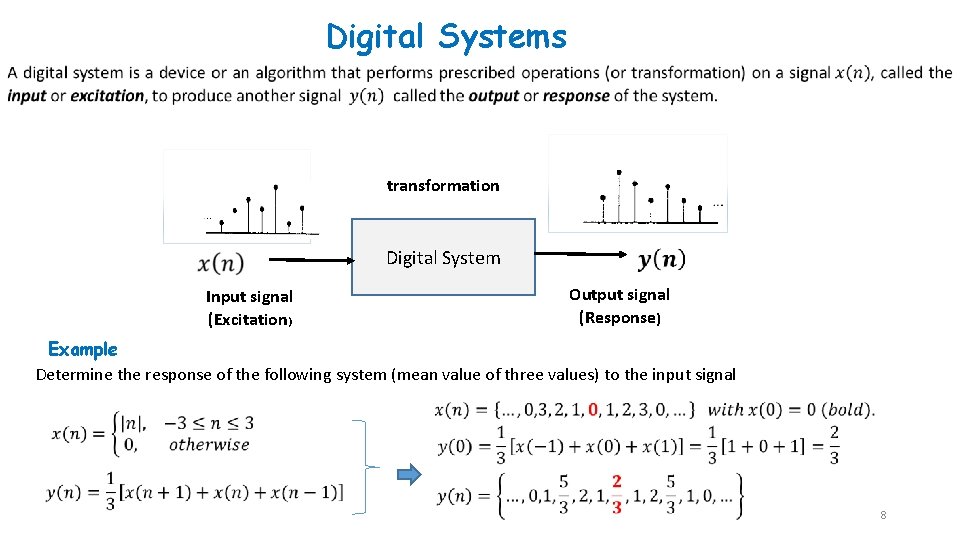
Digital Systems transformation Digital System Input signal (Excitation) Output signal (Response) Example Determine the response of the following system (mean value of three values) to the input signal 8

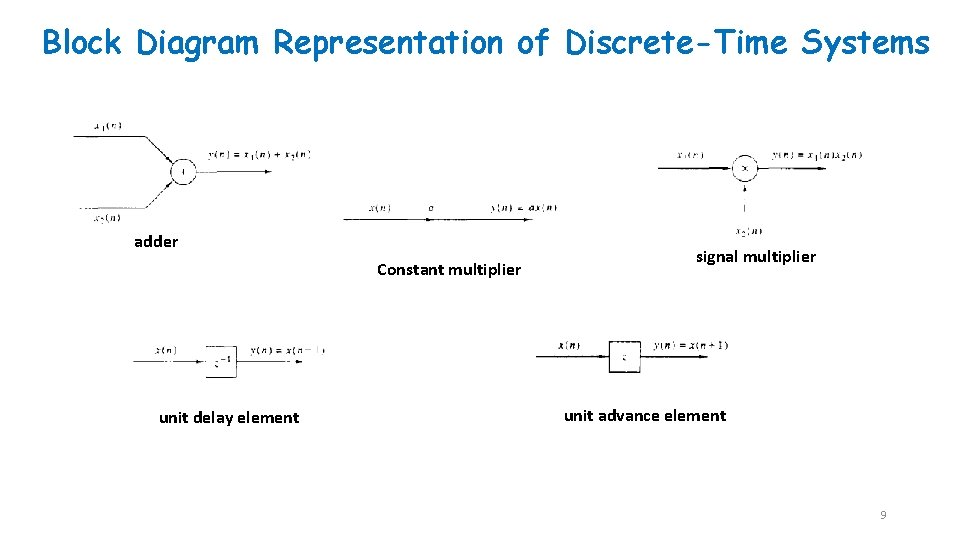
Block Diagram Representation of Discrete-Time Systems adder Constant multiplier unit delay element signal multiplier unit advance element 9

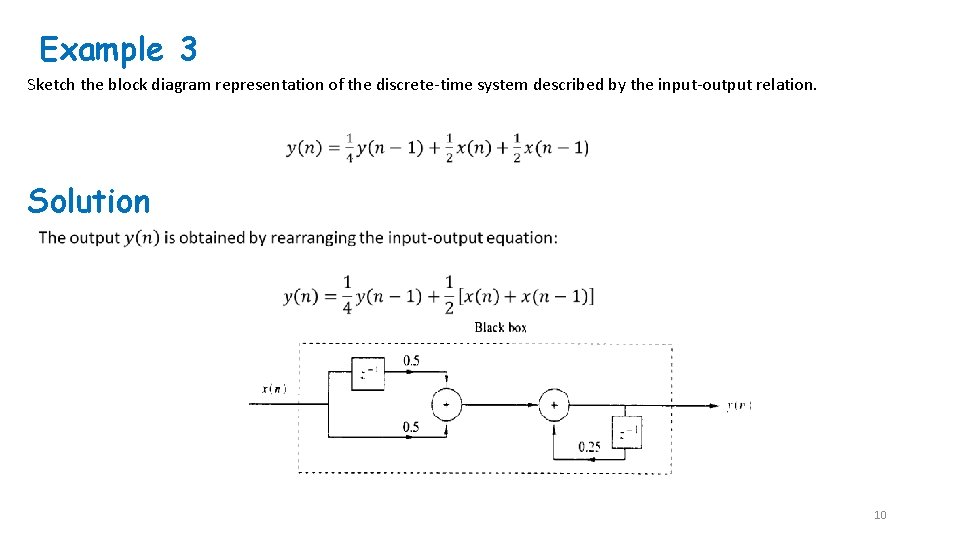
Example 3 Sketch the block diagram representation of the discrete-time system described by the input-output relation. Solution 10

Causal and non-causal systems Example 4 Determine whether the systems described below are causal 11

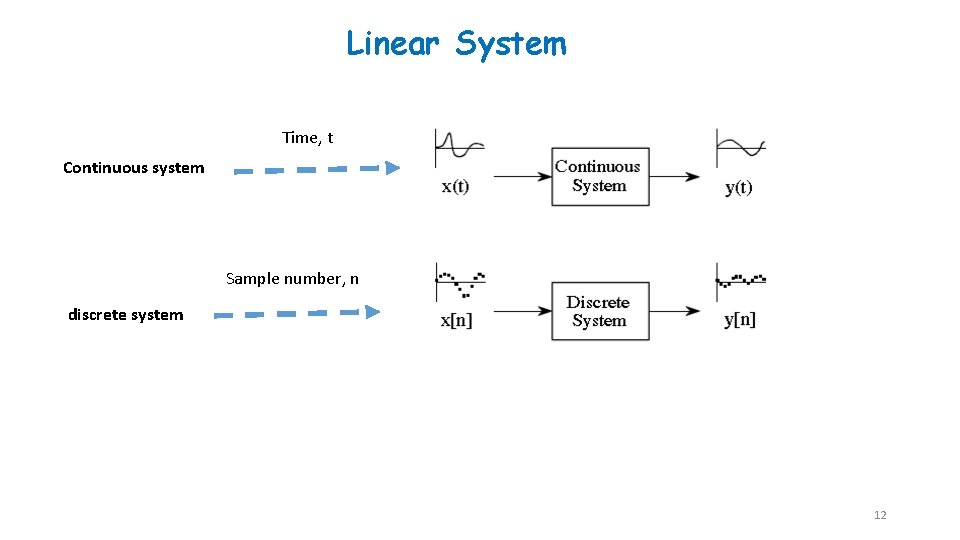
Linear System Time, t Continuous system Sample number, n discrete system 12

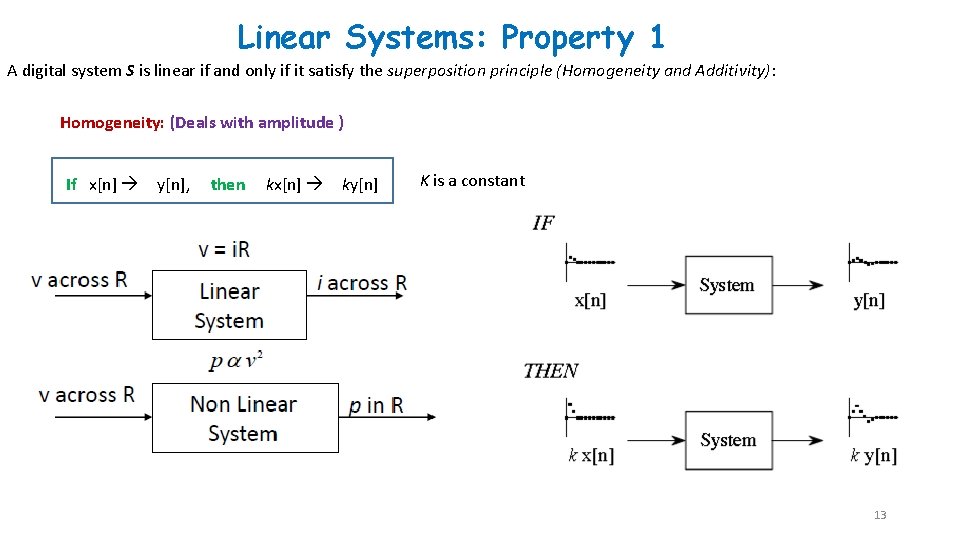
Linear Systems: Property 1 A digital system S is linear if and only if it satisfy the superposition principle (Homogeneity and Additivity): Homogeneity: (Deals with amplitude ) If x[n] y[n], then kx[n] ky[n] K is a constant 13

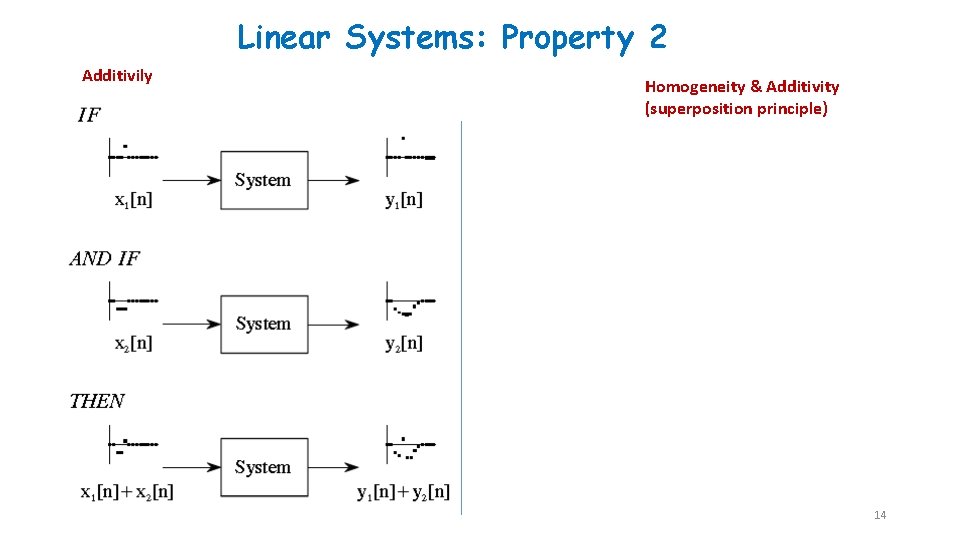
Linear Systems: Property 2 Additivily Homogeneity & Additivity (superposition principle) 14

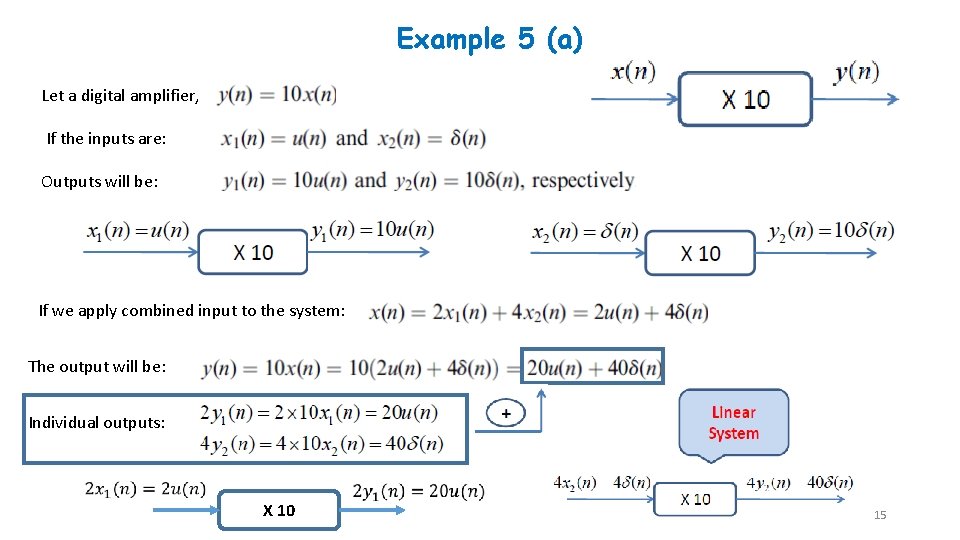
Example 5 (a) Let a digital amplifier, If the inputs are: Outputs will be: If we apply combined input to the system: The output will be: Individual outputs: X 10 15

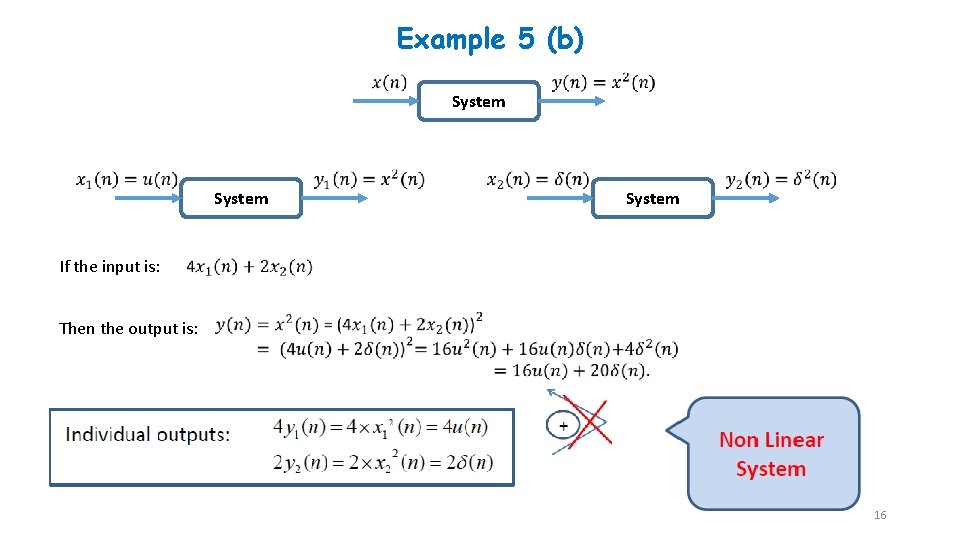
Example 5 (b) System If the input is: Then the output is: 16

Linear Systems: Property 3 Shift (time) Invariance A system is called time-invariant (or shift-invariant) if its input-output characteristics do not change with time (a shifted input signal will produce a shifted output signal, with the same of shifting amount). 17

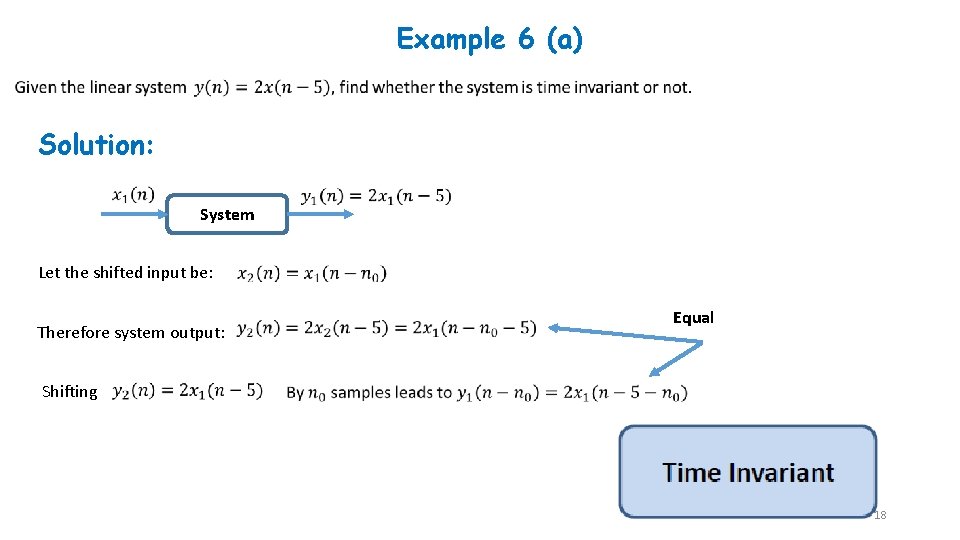
Example 6 (a) Solution: System Let the shifted input be: Therefore system output: Equal Shifting 18

Example 6 (b) Solution: System Let the shifted input be: Therefore system output: Not Equal Shifting 19

Difference Equation A causal, linear, and time invariant system can be represented by a difference equation as follows: Outputs Inputs After rearranging: Finally: 20

Example 7 Identify non zero system coefficients of the following difference equations. 21

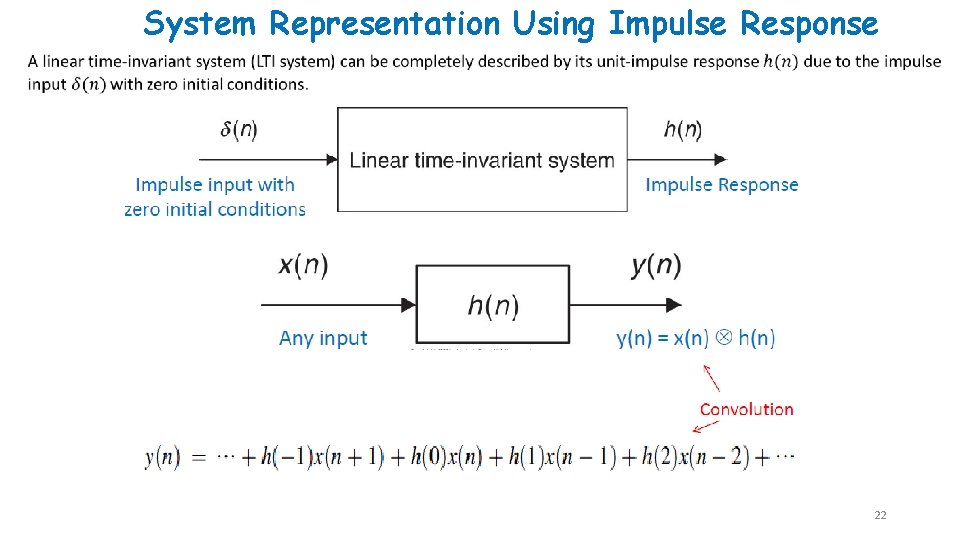
System Representation Using Impulse Response 22

Example 8 (a) Solution 23

Example 8 (b) Solution 24

Finite Impulse Response (FIR) system: Infinite Impulse Response (IIR) system: 25

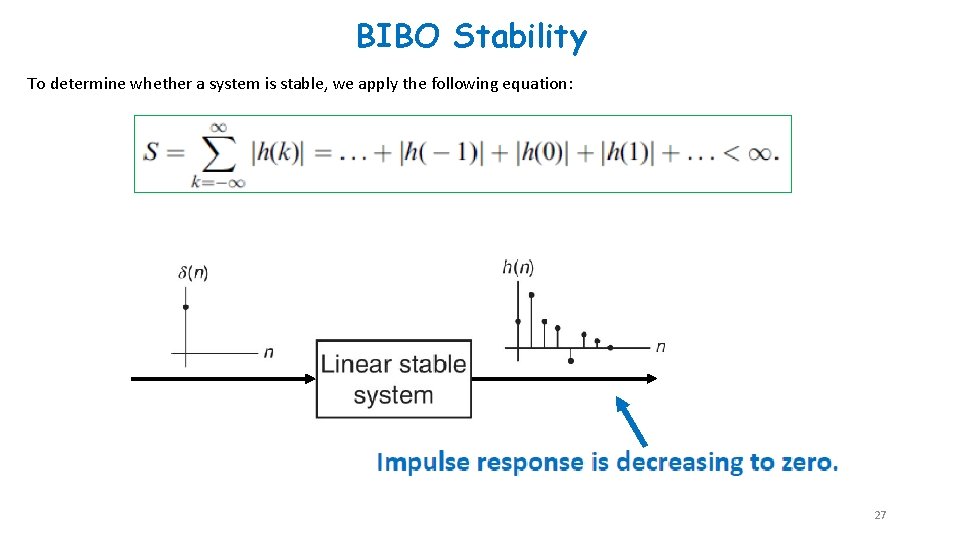
BIBO Stability BIBO: Bounded In and Bounded Out A stable system is one for which every bounded input produces a bounded output. Let, in the worst case, every input value reaches to maximum value M. Using absolute values of the impulse responses, 26

BIBO Stability To determine whether a system is stable, we apply the following equation: 27

Example 9 Given a linear system given by: Which is described by the unit-impulse response: Determine whether the system is stable or not. Solution 28

Digital Convolution The sequences are interchangeable. Convolution sum requires h(n) to be reversed and shifted. If h(n) is the given sequence, h(-n) is the reversed sequence. 29

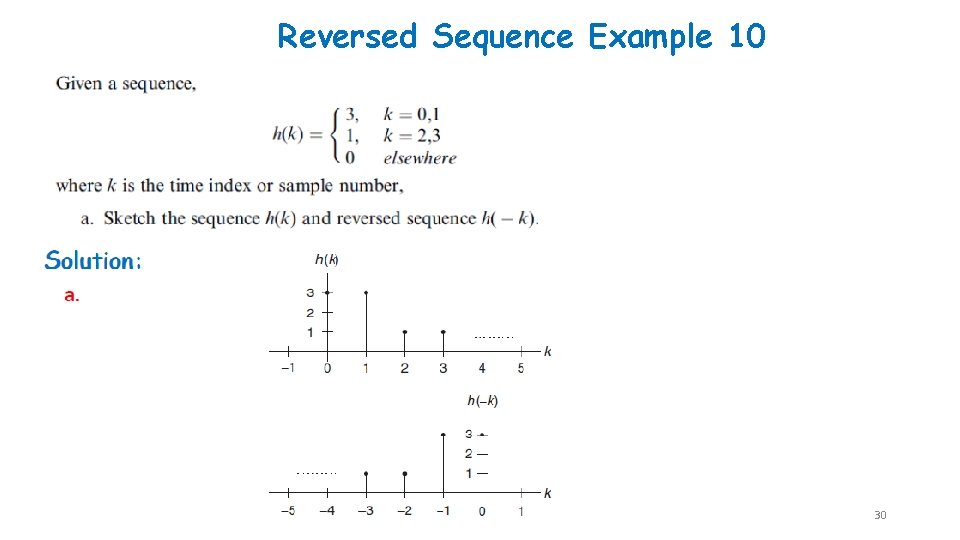
Reversed Sequence Example 10 30

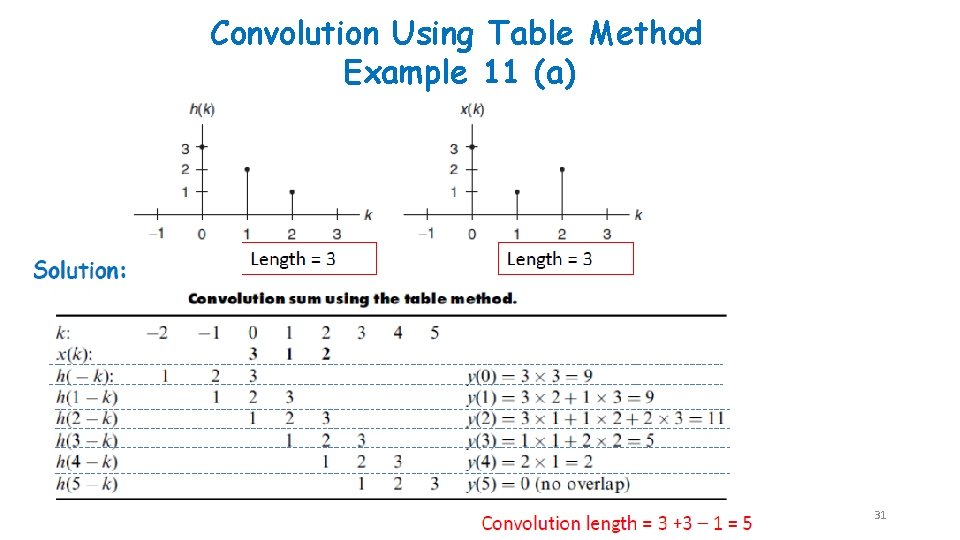
Convolution Using Table Method Example 11 (a) 31

Convolution Using Table Method Example 11 (b) 32

Convolution Properties the order in which two signals are convolved makes no difference 33

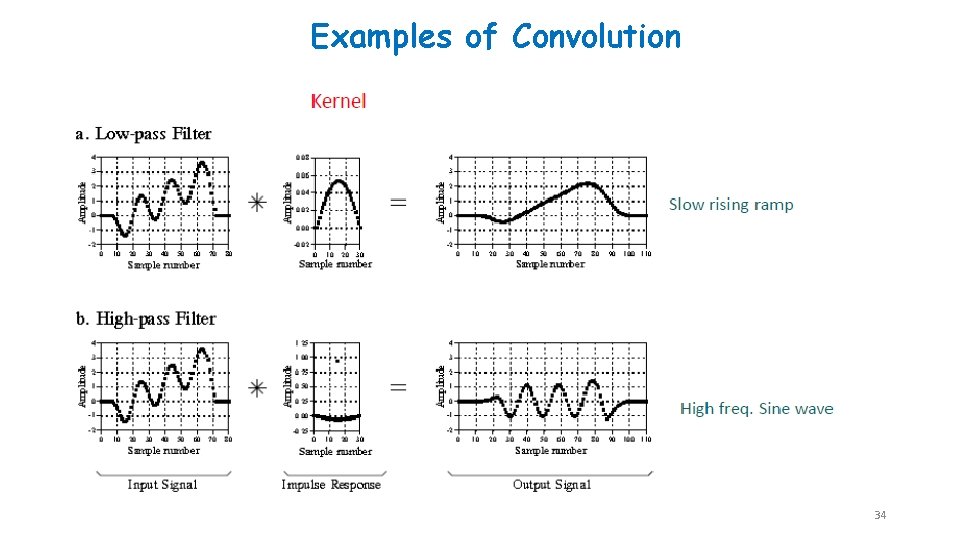
Examples of Convolution 34

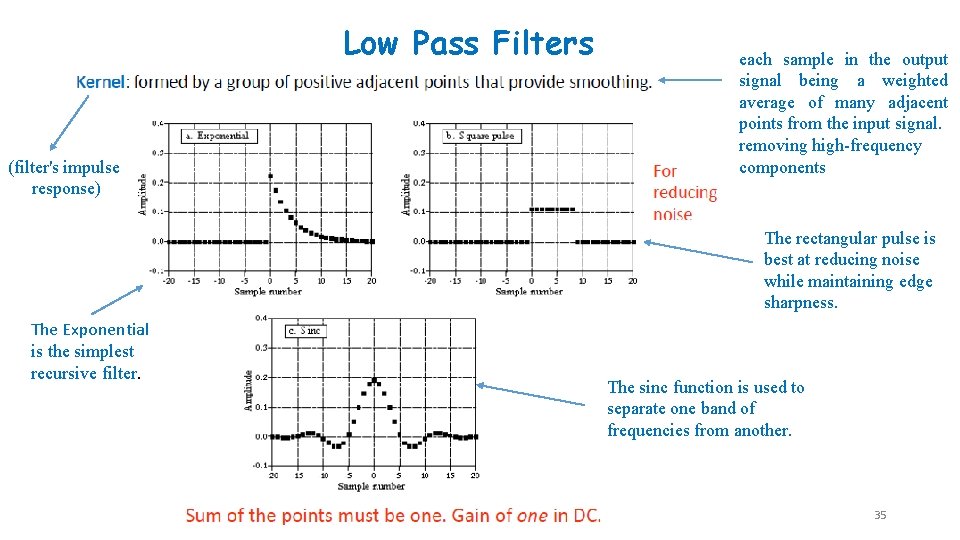
Low Pass Filters (filter's impulse response) each sample in the output signal being a weighted average of many adjacent points from the input signal. removing high-frequency components The rectangular pulse is best at reducing noise while maintaining edge sharpness. The Exponential is the simplest recursive filter. The sinc function is used to separate one band of frequencies from another. 35

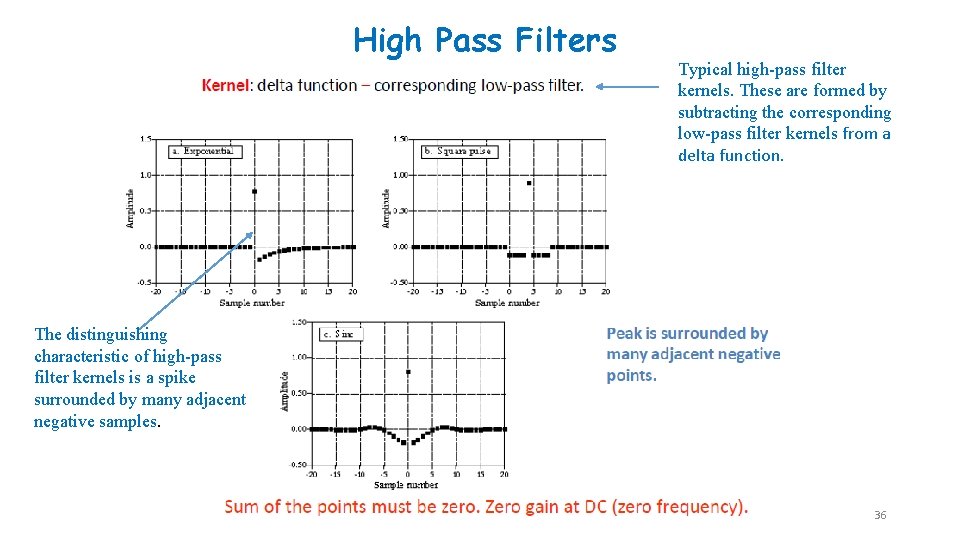
High Pass Filters Typical high-pass filter kernels. These are formed by subtracting the corresponding low-pass filter kernels from a delta function. The distinguishing characteristic of high-pass filter kernels is a spike surrounded by many adjacent negative samples. 36

Signal-to-Noise Ratio (SNR) Signal-to-noise ratio ( SNR) is a measure that compares the level of a desired signal to the level of background noise. It is defined as the ratio of signal power to the noise power, often expressed in decibels. If the variance of the signal and noise are known, and the signal is zero-mean: Because many signals have a very wide dynamic range, SNRs are often expressed using the logarithmic decibel scale. In decibels, the SNR is defined as A logarithmic scale is a nonlinear scale used when there is a large range of quantities. 37

Signal-to-Noise Ratio (SNR) The decibel (d. B) is a logarithmic unit used to express the ratio between two values of a physical quantity, often power or intensity. 38

Example 12 Periodicity Consider the following continuous signal for the current which is sampled at 12. 5 ms. Will the resulting discrete signal be periodic? 39