DIGITAL SIGNAL PROCESSING UNIT I DSP PRELIMINARIES Sampling

DIGITAL SIGNAL PROCESSING

UNIT I: DSP PRELIMINARIES Sampling sampling theorem in time domain recovery of analog signals mapping between analog frequencies to digital frequency concept of Basis function and orthogonality Basic elements of DSP and its requirements advantages of Digital over Analog signal processing 2

WITHOUT DSP? ? ? ? We would not have � Digital/internet audio or video � Digital recording, CD, DVD, MP 3 players � Digital cameras � Digital and cellular telephones � Digital satellite and TV � powerful tools to analyze, visualize data � Image and video editing systems Medical instruments would be less efficient or unable to provide useful information for precise diagnosis (digital ECG analyzer, digital X-ray, medical imaging systems……. . ) 3

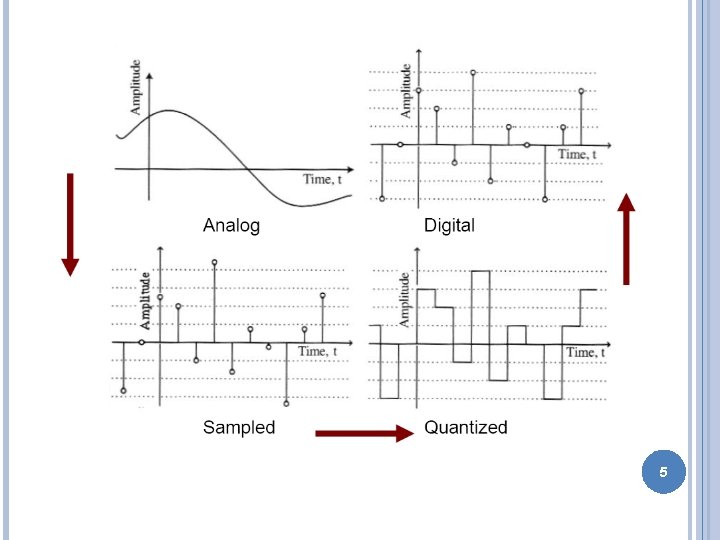
DIGITAL SIGNAL Signal: a function of independent variables (time, distance, position…. ) Independent variable-Continuous/discrete Discrete time signal �A sequence of numbers Analog signal � continuous time signal with continuous amplitude Digital Signal �A discrete time signal with discrete valued amplitudes 4

5

WHY PROCESSING To obtain better quality signal � E. g. noise filtering Signal Processing Analog Digital Mixed 6

ANALOG SIGNAL PROCESSING Most of the natural signals are analog � Analog signal processing Differentiation, Integration, Filtering, Amplification Implemented via passive or active electronic circuitry. 7

DIGITAL SIGNAL PROCESSING Digital signal (rainfall data) Multiplication Addition Delay DSP 8

WHY DSP Cost effective Less sensitive to component tolerances and environmental changes Amenable to full integration � Analog circuits: Inductors and transformers Accuracy can be increased by increasing the word length (cost increases) Dynamic range can be increased by floating point operations Time sharing of a processor is possible (time multiplexing) 9

WHY DSP It permits easy adjustment of processor characteristics during processing (adaptive filters) Exact linear phase system can be designed Multirate processing No loading problems due to cascading Easy storage in magnetic disks, optical disks etc. Very low frequency processing with ease � In analog processing, inductor poses a problem 10

DSP DISADVANTAGES Increased complexity � Need additional pre, post processing devices: ADC, DAC, filters etc. Limited range of frequencies � Frequency range is determined by S/H circuit and A/D converter Power dissipation is major challenge for DSP engineers 11

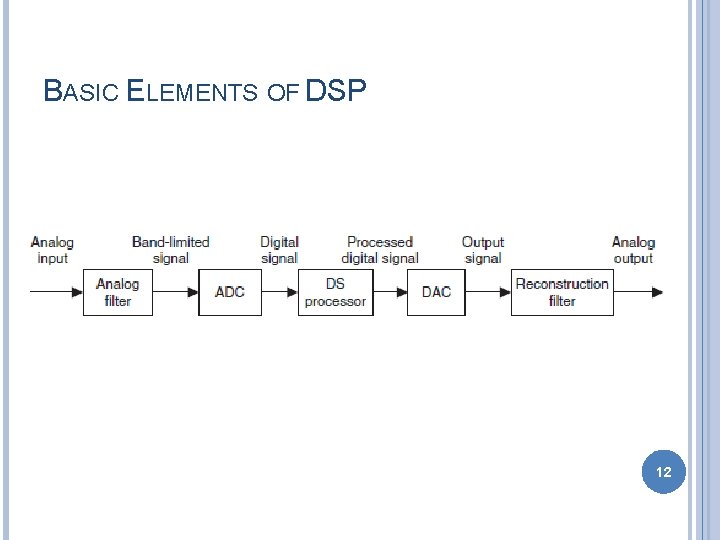
BASIC ELEMENTS OF DSP 12

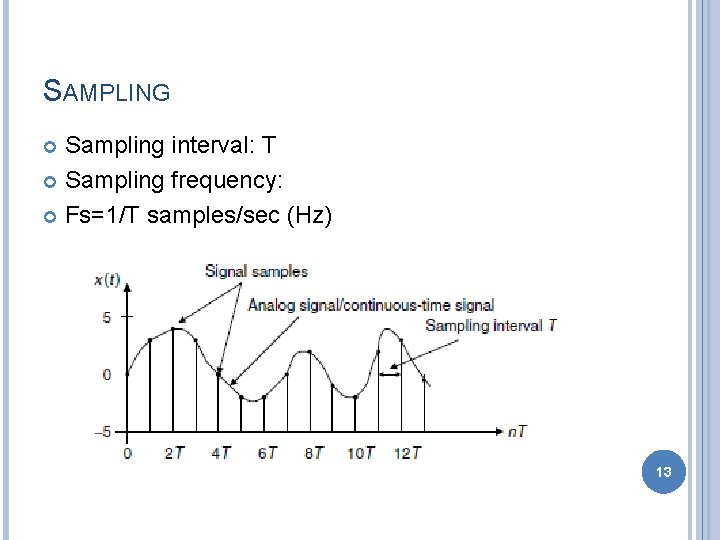
SAMPLING Sampling interval: T Sampling frequency: Fs=1/T samples/sec (Hz) 13

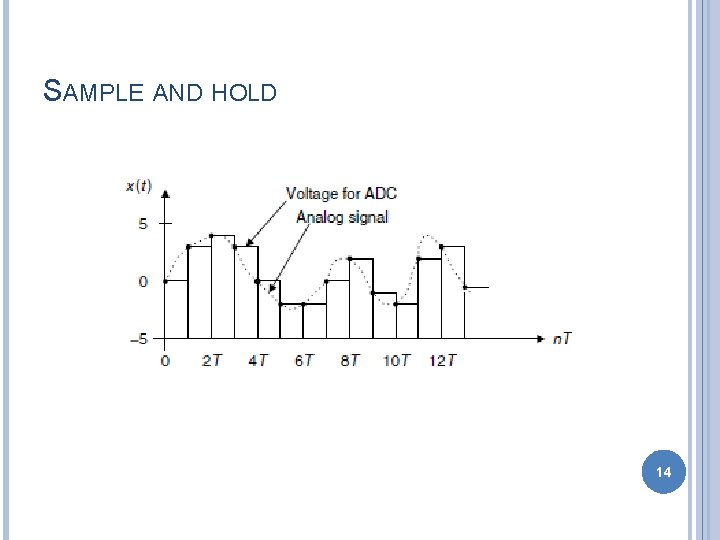
SAMPLE AND HOLD 14

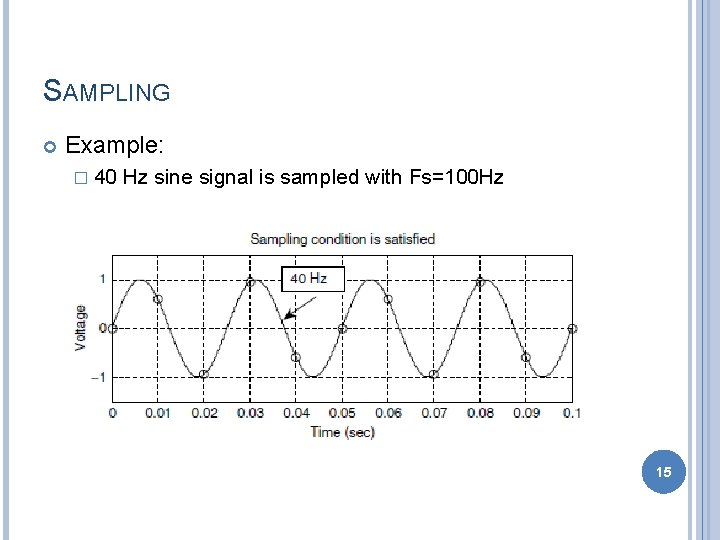
SAMPLING Example: � 40 Hz sine signal is sampled with Fs=100 Hz 15

PERIODIC (UNIFORM) SAMPLING Sampled signal, 16

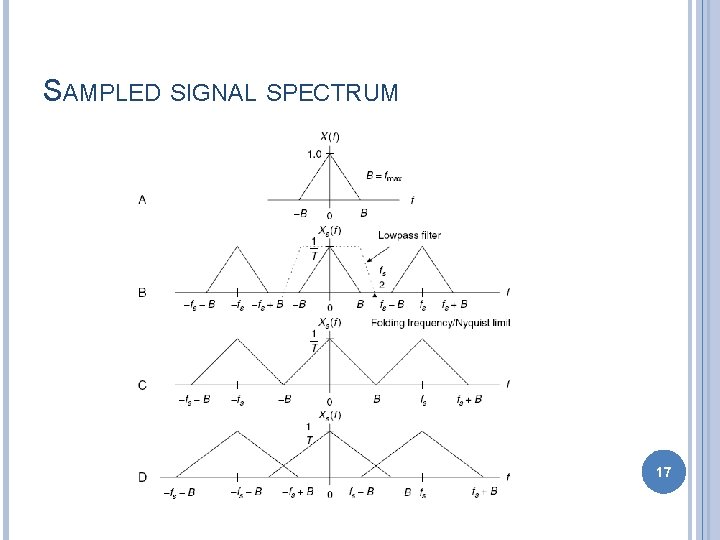
SAMPLED SIGNAL SPECTRUM 17

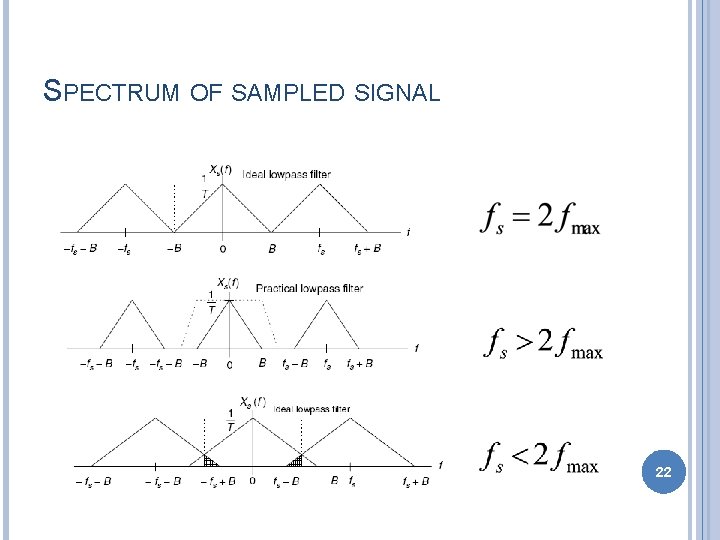
SAMPLING THEOREM A band limited continuous time signal with highest frequency fmax Hz, can be uniquely recovered from its samples provided that the sampling rate fs is greater than or equal to 2 fmax samples per second Nyquist rate: Nyquist limit/Folding frequency 18

EXAMPLE Sketch the spectrum of the signal, Sketch the spectrum of the above signal if it is sampled at the rate of 8000 Hz 19

SOLUTION 20

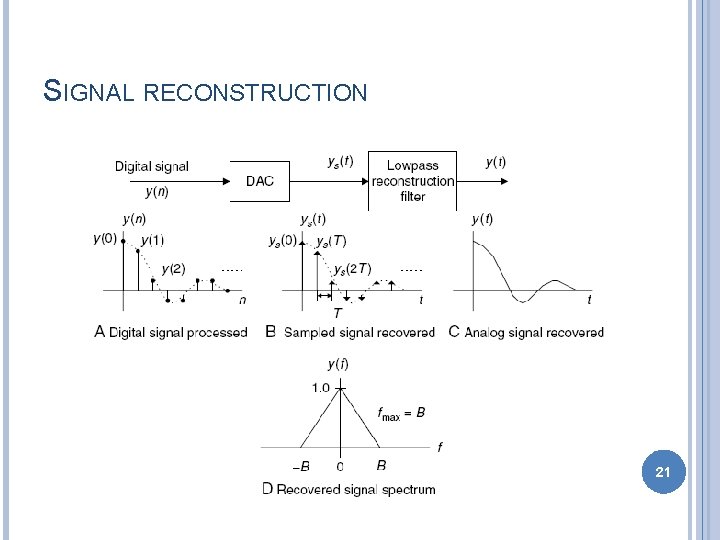
SIGNAL RECONSTRUCTION 21

SPECTRUM OF SAMPLED SIGNAL 22

ALIASING If an analog signal with frequency f is under sampled, the aliasing frequency component falias in the baseband is given by 23

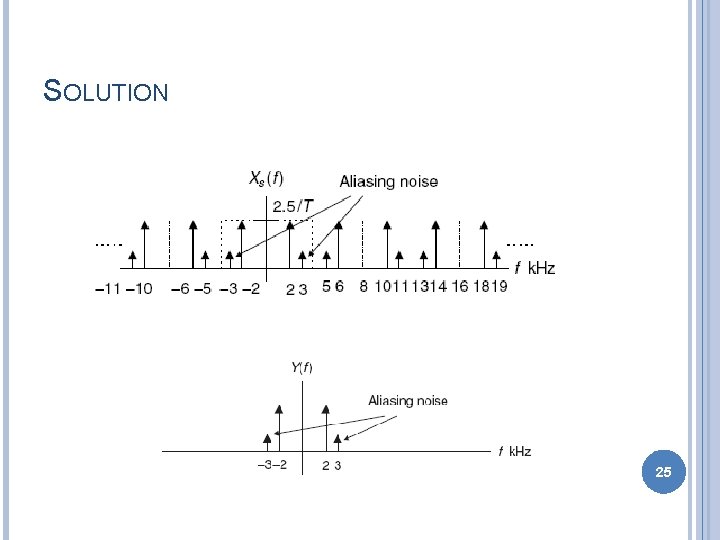
EXAMPLE Sketch the spectrum of the signal, Sketch the spectrum of the above signal if it is sampled at the rate of 8000 Hz Sketch the recovered analog signal spectrum, if an ideal low pass filter with cut off frequency of 4 KHz is used to recover original signal 24

SOLUTION 25

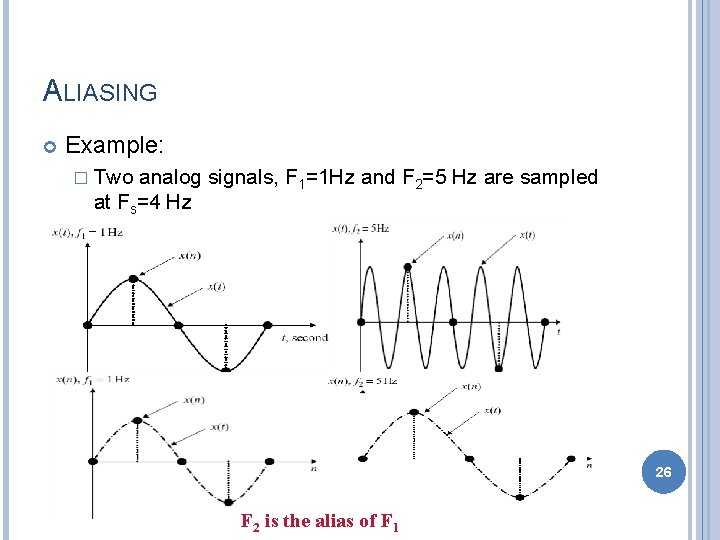
ALIASING Example: � Two analog signals, F 1=1 Hz and F 2=5 Hz are sampled at Fs=4 Hz 26 F 2 is the alias of F 1

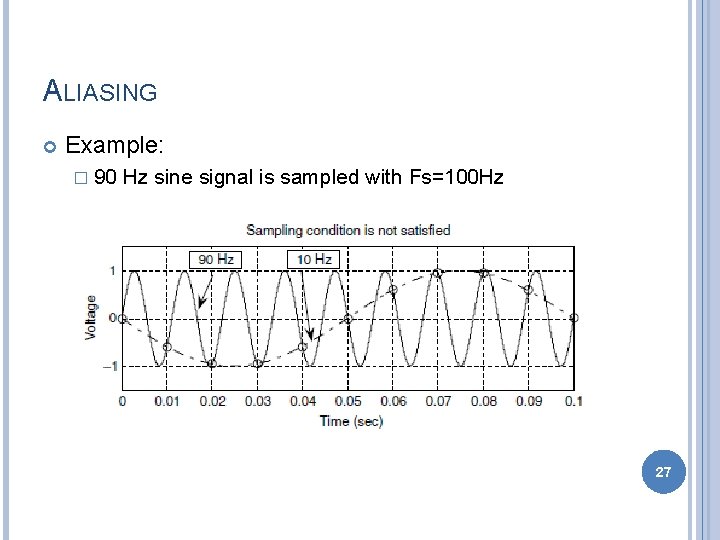
ALIASING Example: � 90 Hz sine signal is sampled with Fs=100 Hz 27

ALIAS DEMO The video camera is sampling at a fixed rate of 30 frames/second. Observe how the rotating phasor aliases to different speeds as it spins faster. 28

SIGNAL REPRESENTATION Notations: � Analog signal: � Digital Signal: Signal representation Units 29

RELATIONS What is the relation between F and f What is the relation between t and n and 30

FREQUENCY RANGES What is the frequency range of and 31

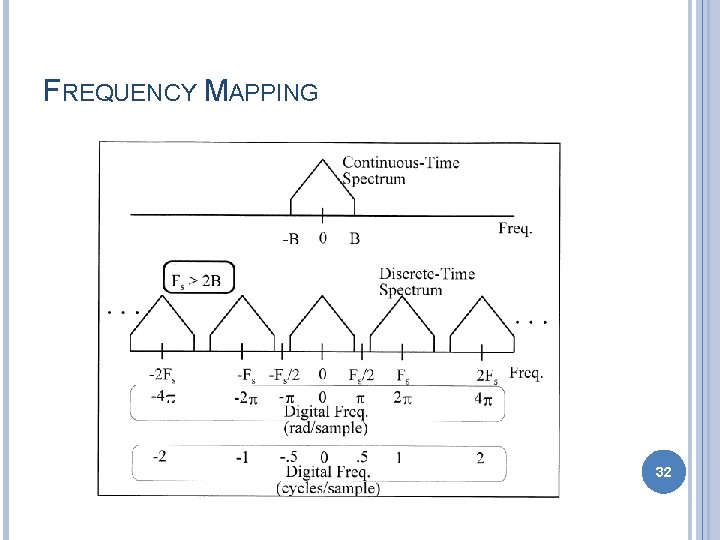
FREQUENCY MAPPING 32

RELATIONS AMONG FREQUENCY VARIABLES 33

BASIS FUNCTIONS In mathematics, a basis function is an element of a particular basis for a function space. Every continuous function in the function space can be represented as a linear combination of basis functions, just as every vector in a vector space can be represented as a linear combination of basis vectors. 34

BASICS 35

ORTHOGONALITY Two vectors v 1 and v 2 are orthogonal if v 1 and v 2 are orthonormal if they are orthogonal and 36

EXAMPLES 37

EXAMPLES 38

FOURIER SERIES 39

THANK YOU 40