Digital Signal Processing II Lecture 7 Maximally Decimated

Digital Signal Processing II Lecture 7: Maximally Decimated Filter Banks Marc Moonen Dept. E. E. /ESAT, K. U. Leuven marc. moonen@esat. kuleuven. be www. esat. kuleuven. be/scd/

Part-II : Filter Banks Lecture-6 : Preliminaries • Filter bank set-up and applications • `Perfect reconstruction’ problem + 1 st example (DFT/IDFT) • Multi-rate systems review (10 slides) Lecture-7 : Maximally decimated FBs • Perfect reconstruction filter banks (PR FBs) • Paraunitary PR FBs Lecture-8 : Modulated FBs • DFT-modulated FBs • Oversampled DFT-modulated FBs Lecture-9 : Special Topics • Cosine-modulated FBs • Non-uniform FBs & Wavelets • Frequency domain filtering DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 2

PART-II : Filter Banks LECTURE-7 : Maximally decimated FBs • Perfect reconstruction (PR) – 2 -channel case – M-channel case • `Interludium’: Paraconjugation & paraunitary functions • Paraunitary PR FBs DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 3

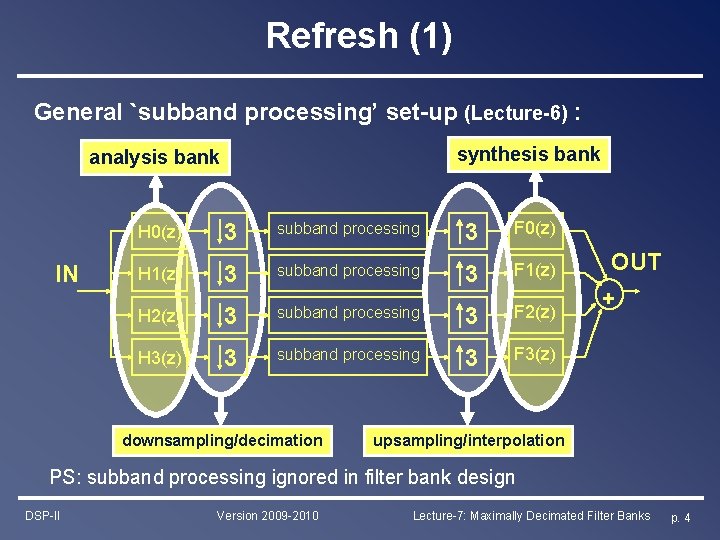
Refresh (1) General `subband processing’ set-up (Lecture-6) : synthesis bank analysis bank IN H 0(z) 3 subband processing 3 F 0(z) H 1(z) 3 subband processing 3 F 1(z) H 2(z) 3 subband processing 3 F 2(z) H 3(z) 3 subband processing 3 F 3(z) downsampling/decimation OUT + upsampling/interpolation PS: subband processing ignored in filter bank design DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 4

Refresh (2) Two design issues : - filter specifications, e. g. stopband attenuation, passband ripple, transition band, etc. (for each (analysis) filter!) - perfect reconstruction property. PS: Perfect reconstruction property as such is easily satisfied, if there aren’t any (analysis) filter specs, e. g. (see Lecture-6) u[k] 4 4 4 4 + u[k-3] …but this is not very useful/practical. Tight filter specs. necessary for subband coding, etc. This lecture : Maximally decimated FB’s : DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 5

PS: Filter bank set-up revisited IN H 1(z) 4 subband processing 4 G 1(z) H 2(z) 4 subband processing 4 G 2(z) H 3(z) 4 subband processing 4 G 3(z) H 4(z) 4 subband processing 4 G 4(z) OUT + - analysis filters Hi(z) are also decimation (anti-aliasing) filters, to avoid aliased contributions in subband signals - synthesis filters Gi(z) are also interpolation filters, to remove images after expanders (upsampling) DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 6

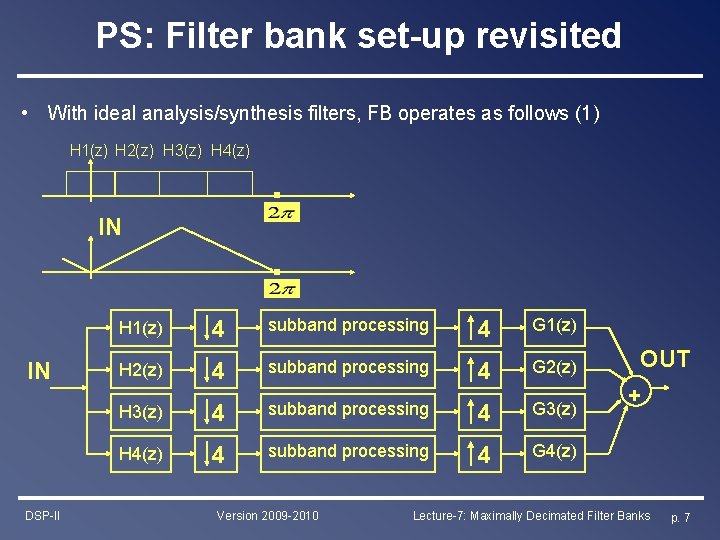
PS: Filter bank set-up revisited • With ideal analysis/synthesis filters, FB operates as follows (1) H 1(z) H 2(z) H 3(z) H 4(z) IN IN DSP-II H 1(z) 4 subband processing 4 G 1(z) H 2(z) 4 subband processing 4 G 2(z) H 3(z) 4 subband processing 4 G 3(z) H 4(z) 4 subband processing 4 G 4(z) Version 2009 -2010 OUT + Lecture-7: Maximally Decimated Filter Banks p. 7

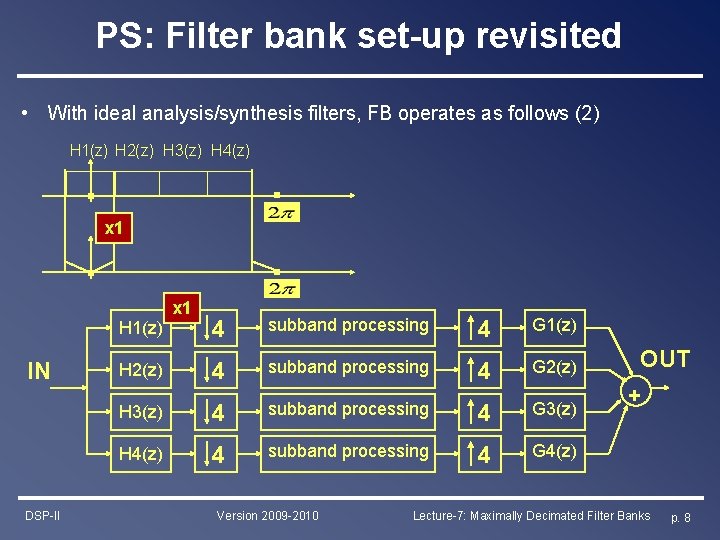
PS: Filter bank set-up revisited • With ideal analysis/synthesis filters, FB operates as follows (2) H 1(z) H 2(z) H 3(z) H 4(z) x 1 IN DSP-II H 1(z) 4 subband processing 4 G 1(z) H 2(z) 4 subband processing 4 G 2(z) H 3(z) 4 subband processing 4 G 3(z) H 4(z) 4 subband processing 4 G 4(z) Version 2009 -2010 OUT + Lecture-7: Maximally Decimated Filter Banks p. 8

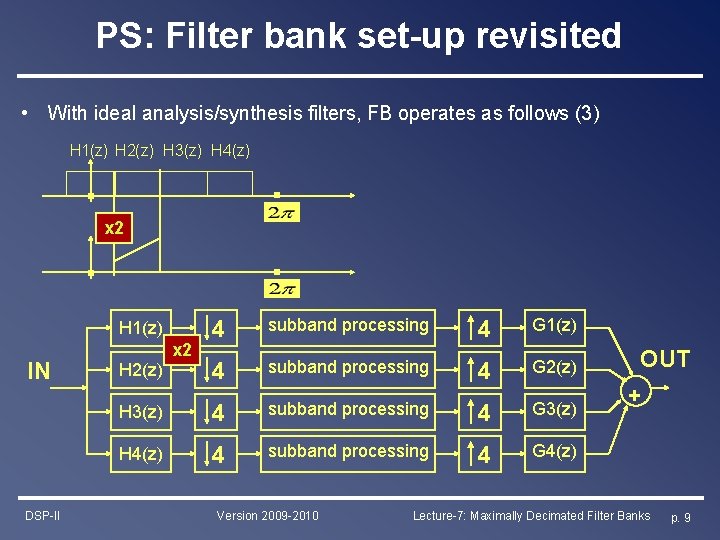
PS: Filter bank set-up revisited • With ideal analysis/synthesis filters, FB operates as follows (3) H 1(z) H 2(z) H 3(z) H 4(z) x 2 4 subband processing 4 G 1(z) 4 subband processing 4 G 2(z) H 3(z) 4 subband processing 4 G 3(z) H 4(z) 4 subband processing 4 G 4(z) H 1(z) IN DSP-II H 2(z) x 2 Version 2009 -2010 OUT + Lecture-7: Maximally Decimated Filter Banks p. 9

PS: Filter bank set-up revisited • With ideal analysis/synthesis filters, FB operates as follows (4) x’ 1 (ideal subband processing) IN DSP-II x’ 1 4 G 1(z) subband processing 4 G 2(z) 4 subband processing 4 G 3(z) 4 subband processing 4 G 4(z) H 1(z) 4 H 2(z) 4 H 3(z) H 4(z) subband processing Version 2009 -2010 OUT + Lecture-7: Maximally Decimated Filter Banks p. 10

PS: Filter bank set-up revisited • With ideal analysis/synthesis filters, FB operates as follows (5) x’ 2 H 1(z) IN DSP-II 4 subband processing x’ 2 4 G 1(z) 4 G 2(z) H 2(z) 4 H 3(z) 4 subband processing 4 G 3(z) H 4(z) 4 subband processing 4 G 4(z) Version 2009 -2010 OUT + Lecture-7: Maximally Decimated Filter Banks p. 11

PS: Filter bank set-up revisited • With ideal analysis/synthesis filters, FB operates as follows (6) x’’ 1 (ideal subband processing) IN DSP-II x’’ 1 H 1(z) 4 subband processing 4 G 1(z) H 2(z) 4 subband processing 4 G 2(z) H 3(z) 4 subband processing 4 G 3(z) H 4(z) 4 subband processing 4 G 4(z) Version 2009 -2010 OUT + Lecture-7: Maximally Decimated Filter Banks p. 12

PS: Filter bank set-up revisited • With ideal analysis/synthesis filters, FB operates as follows (7) x’’ 2 IN DSP-II G 1(z) 4 subband processing H 2(z) 4 subband processing 4 H 3(z) 4 subband processing 4 G 3(z) H 4(z) 4 subband processing 4 G 4(z) H 1(z) Version 2009 -2010 4 x’’ 2 G 2(z) OUT + Lecture-7: Maximally Decimated Filter Banks p. 13

PS: Filter bank set-up revisited • With ideal analysis/synthesis filters, FB operates as follows (8) G 1(z) G 2(z) G 3(z) G 4(z) x’’’ 1 (ideal subband processing) IN DSP-II H 1(z) 4 subband processing 4 G 1(z) H 2(z) 4 subband processing 4 G 2(z) H 3(z) 4 subband processing 4 G 3(z) H 4(z) 4 subband processing 4 G 4(z) Version 2009 -2010 x’’’ 1 OUT + Lecture-7: Maximally Decimated Filter Banks p. 14

PS: Filter bank set-up revisited • With ideal analysis/synthesis filters, FB operates as follows (9) G 1(z) G 2(z) G 3(z) G 4(z) x’’’ 2 IN DSP-II H 1(z) 4 subband processing 4 H 2(z) 4 subband processing 4 G 1(z) x’’’ 2 G 2(z) H 3(z) 4 subband processing 4 G 3(z) H 4(z) 4 subband processing 4 G 4(z) Version 2009 -2010 OUT + Lecture-7: Maximally Decimated Filter Banks p. 15

PS: Filter bank set-up revisited • With ideal analysis/synthesis filters, FB operates as follows (10) H 1(z) H 2(z) H 3(z) H 4(z) OUT=IN IN DSP-II H 1(z) 4 subband processing 4 G 1(z) H 2(z) 4 subband processing 4 G 2(z) H 3(z) 4 subband processing 4 G 3(z) H 4(z) 4 subband processing 4 G 4(z) Version 2009 -2010 OUT + Now try this with. Maximally non-ideal filters… Lecture-7: Decimated Filter Banks p. 16

Perfect Reconstruction : 2 -Channel Case u[k] H 0(z) H 1(z) It is proved that. . . 2 2 2 F 0(z) 2 F 1(z) y[k] + (try it!) • U(-z) represents aliased signals, hence the `alias transfer function’ A(z) should ideally be zero • T(z) is referred to as `distortion function’ (amplitude & phase distortion). For perfect reconstruction, T(z) should ideally be a pure delay DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 17

Perfect Reconstruction : 2 -Channel Case u[k] H 0(z) H 1(z) 2 2 2 F 0(z) 2 F 1(z) y[k] + • Requirement for `alias-free’ filter bank : If A(z)=0, then Y(z)=T(z). U(z), hence the complete filter bank behaves as a linear time invariant (LTI) system (despite up- & downsampling) !!!! • Requirement for `perfect reconstruction’ filter bank (= alias-free + distortion-free): i) ii) DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 18

Perfect Reconstruction : 2 -Channel Case u[k] H 0(z) H 1(z) 2 2 2 F 0(z) 2 F 1(z) y[k] + • A first attempt is as follows…. . : so that For the real coefficient case, i. e. which means the amplitude response of H 1 is the mirror image of the amplitude response of Ho with respect to the quadrature frequency hence the name `quadrature mirror filter’ (QMF) DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 19

Perfect Reconstruction : 2 -Channel Case u[k] H 0(z) H 1(z) `quadrature mirror filter’ (QMF) : 2 2 Ho 2 F 0(z) 2 F 1(z) y[k] + H 1 hence if Ho (=Fo) is designed to be a good lowpass filter, then H 1 (=-F 1) is a good high-pass filter. DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 20

Perfect Reconstruction : 2 -Channel Case • A 2 nd (better) attempt is as follows: [Smith & Barnwell 1984] [Mintzer 1985] i) so that (alias cancellation) ii) `power symmetric’ Ho(z) (real coefficients case) iii) so that (distortion function) ignore the details! This is a so-called`paraunitary’ perfect reconstruction bank (see below), based on a lossless system Ho, H 1 : DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks This is already pretty complicated… p. 21

Perfect Reconstruction : M-Channel Case u[k] H 0(z) 4 4 F 0(z) H 1(z) 4 4 F 1(z) H 2(z) 4 4 F 2(z) H 3(z) 4 4 F 3(z) It is proved that. . . y[k] + (try it!) • 2 nd term represents aliased signals, hence all `alias transfer functions’ Al(z) should ideally be zero (for all l ) • H(z) is referred to as `distortion function’ (amplitude & phase distortion). For perfect reconstruction, H(z) should ideally be a pure delay DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks Sigh !!… p. 22

Perfect Reconstruction : M-Channel Case • A simpler analysis results from a polyphase description : 4 4 u[k] 4 4 + u[k-3] i-th row of E(z) has polyphase components of Hi(z) i-th column of R(z) has polyphase components of Fi(z) DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 23 Do not continue until you understand how formulae correspond to block scheme!

Perfect Reconstruction : M-Channel Case • with the `noble identities’, this is equivalent to: u[k] 4 4 4 4 + u[k-3] Necessary & sufficient conditions for i) alias cancellation ii) perfect reconstruction are then derived, based on the product DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 24

Perfect Reconstruction : M-Channel Case u[k] 4 4 4 4 + u[k-3] Necessary & sufficient condition for alias-free FB is…: a pseudo-circulant matrix is a circulant matrix with the additional feature that elements below the main diagonal are multiplied by 1/z, i. e. . . and first row of R(z). E(z) are polyphase cmpnts of `distortion function’ T(z) read on-> DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 25

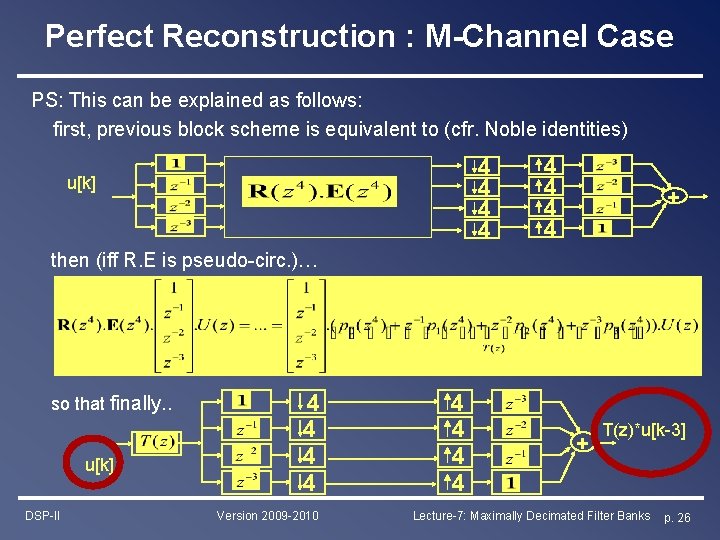
Perfect Reconstruction : M-Channel Case PS: This can be explained as follows: first, previous block scheme is equivalent to (cfr. Noble identities) 4 4 u[k] 4 4 + then (iff R. E is pseudo-circ. )… so that finally. . u[k] DSP-II 4 4 Version 2009 -2010 4 4 + T(z)*u[k-3] Lecture-7: Maximally Decimated Filter Banks p. 26

Perfect Reconstruction : M-Channel Case 4 4 u[k] 4 4 + u[k-3] Hence necessary & sufficient condition for PR (where T(z)=pure delay): I_n is nxn identity matrix, r is arbitrary Example (r=0) : DSP-II for conciseness, will use this from now on ! Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 27

Perfect Reconstruction : M-Channel Case • Example : DFT/IDFT Filter bank (Lecture-6) : E(z)=F , R(z)=F^-1 • Design Procedure: 1. Design all analysis filters (see Part-I). 2. This determines E(z) (=polyphase matrix). 3. Assuming E(z) can be inverted (? ), synthesis filters are • Will consider only FIR analysis filters, leading to simple polyphase decompositions (see Lecture-6). However, FIR E(Z) generally leads to IIR R(z), where stability is a concern… DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 28

Perfect Reconstruction : M-Channel Case PS: Inversion of matrix transfer functions ? … – The inverse of a scalar (i. e. 1 -by-1 matrix) FIR transfer function is always IIR (except for contrived examples) – The inverse of an N-by-N (N>1) FIR transfer function can be FIR DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 29

Perfect Reconstruction : M-Channel Case PS: Inversion of matrix transfer functions ? … Compare this to inversion of integers and integer matrices: – The inverse of an integer is always non-integer (except for `E=1’) – The inverse of an N-by-N (N>1) integer matrix can be integer DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 30

Perfect Reconstruction : M-Channel Case Question: How can we find polynomial (FIR) matrices E(z) that have a FIR inverse? Answer: `Unimodular’ matrices = matrices with { determinant=constant*z^-d } e. g. where the Ei’s are constant (=not a function of z) invertible matrices Example: E(z) = FIR LPC lattice , see lecture-4 Design Procedure : optimize Ei’s to obtain analysis filter specs (ripple, etc. ), etc. . DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 31

Perfect Reconstruction : M-Channel Case Question: Can we avoid direct inversion, e. g. through the usage FIR E(z) matrices with additional `special properties’, so that R(z) is trivially obtained and its specs are better controlled? (compare with (real) orthogonal or (complex) unitary matrices, where inverse is equal to (Hermitian) transpose) Answer: YES, `paraunitary’ matrices (=special class of FIR matrices with FIR inverse) See next slides…. Will focus on paraunitary E(z) leading to PR/FIR/paraunitary filter banks DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 32

Paraunitary PR Filter Banks Interludium : `PARACONJUGATION’ • For a scalar transfer function H(z), paraconjugate is i. e it is obtained from H(z) by - replacing z by 1/z - replacing each coefficient by its complex conjugate Example : On the unit circle, paraconjugation corresponds to complex conjugation paraconjugation = `analytic extension’ of unit-circle complex conjugation DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 33

Paraunitary PR Filter Banks Interludium : `PARACONJUGATION’ • For a matrix transfer function H(z), paraconjugate is i. e it is obtained from H(z) by - transposition - replacing z by 1/z - replacing each coefficient by is complex conjugate Example : On the unit circle, paraconjugation corresponds to transpose conjugation paraconjugation = `analytic extension’ of unit-circle transpose conjugation DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 34

Paraunitary PR Filter Banks Interludium : `PARAUNITARY matrix transfer functions’ • Matrix transfer function H(z), is paraunitary if (possibly up to a scalar) For a square matrix function A paraunitary matrix is unitary on the unit circle paraunitary = `analytic extension’ of unit-circle unitary. PS: if H 1(z) and H 2(z) are paraunitary, then H 1(z). H 2(z) is paraunitary DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 35

Paraunitary PR Filter Banks 4 4 u[k] 4 4 + u[k-3] - If E(z) is paraunitary then perfect reconstruction is obtained with (delta to make synthesis causal) If E(z) is FIR, then R(z) is also FIR !! (cfr. definition paraconjugation) DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 36

Paraunitary PR Filter Banks • Example: paraunitary FIR E(z) with FIR inverse R(z) where the Ei’s are constant unitary matrices Example: 1 -input/2 -output FIR lossless lattice, see lecture-4, p. 22 Example: 1 -input/M-output FIR lossless lattice, see lecture-4, p. 27 • Design Procedure : optimize unitary Ei’s (e. g. rotation angles in lossless lattices) to obtain analysis filter specs, etc. . DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 37

Paraunitary PR Filter Banks Properties of paraunitary PR filter banks: (proofs omitted) • If polyphase matrix E(z) (and hence E(z^N)) is paranunitary, and then vector transfer function H(z) (=all analysis filters ) is paraunitary • If vector transfer function H(z) is paraunitary, then its components are power complementary (lossless 1 -input/N-output system) (see lecture 4 !!) DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 38

Paraunitary PR Filter Banks Properties of paraunitary PR filter banks (continued): • Synthesis filters are obtained from analysis filters by conjugating the analysis filter coefficients + reversing the order (cfr page 34): • Hence magnitude response of synthesis filter Fk is the same as magnitude response of corresponding analysis filter Hk: • Hence, as analysis filters are power complementary (cfr. supra), synthesis filters are also power complementary • example: DFT/IDFT bank (lecture-6), 2 -channel case (page 21) • Great properties/designs. . DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 39

Conclusions • Have derived general conditions for perfect reconstruction, based on polyphase matrices for analysis/synthesis bank • Seen example of general PR filter bank design : PR/FIR/Paraunitary FBs, e. g. based on FIR lossless lattice filters • Sequel = other (better) PR structures Lecture 7: Modulated filter banks Lecture 8: Oversampled filter banks, etc. . • Reference: `Multirate Systems & Filter Banks’ , P. P. Vaidyanathan Prentice Hall 1993. DSP-II Version 2009 -2010 Lecture-7: Maximally Decimated Filter Banks p. 40