Digital Signal Processing II Lecture 6 Filter Banks

Digital Signal Processing II Lecture 6: Filter Banks - Preliminaries Marc Moonen Dept. E. E. /ESAT, K. U. Leuven marc. moonen@esat. kuleuven. be homes. esat. kuleuven. be/~moonen/

Part-II : Filter Banks Lecture-6 : Preliminaries • Filter bank set-up and applications • `Perfect reconstruction’ problem + 1 st example (DFT/IDFT) • Multi-rate systems review (10 slides) Lecture-7 : Maximally decimated FBs • Perfect reconstruction filter banks (PR FBs) • Paraunitary PR FBs Lecture-8 : Modulated FBs • Maximally decimated DFT-modulated FBs • Oversampled DFT-modulated FBs Lecture-9 : Special Topics • Cosine-modulated FBs • Non-uniform FBs & Wavelets • Frequency domain filtering DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 2

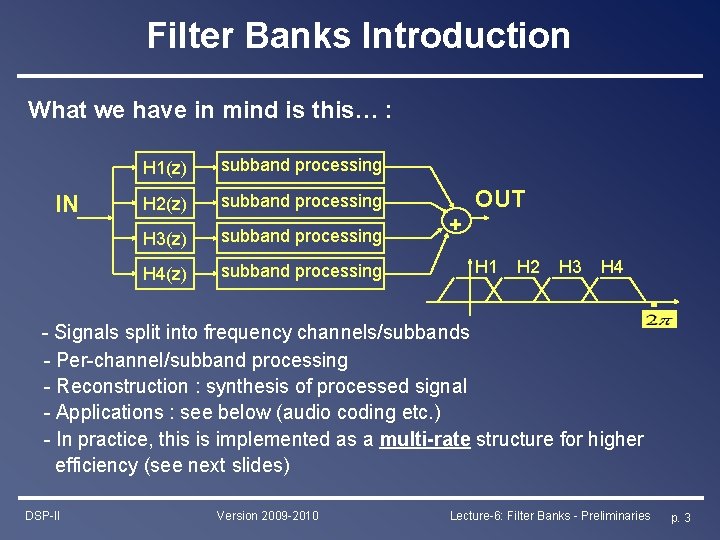
Filter Banks Introduction What we have in mind is this… : IN H 1(z) subband processing H 2(z) subband processing H 3(z) subband processing H 4(z) subband processing + OUT H 1 H 2 H 3 H 4 - Signals split into frequency channels/subbands - Per-channel/subband processing - Reconstruction : synthesis of processed signal - Applications : see below (audio coding etc. ) - In practice, this is implemented as a multi-rate structure for higher efficiency (see next slides) DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 3

Filter Banks Introduction Step-1: Analysis filter bank - collection of M filters (`analysis filters’, `decimation filters’) with a common input signal - ideal (but non-practical) frequency responses = ideal bandpass filters - typical frequency responses (overlapping, non-overlapping, …) M=4 H 1(z) IN H 2(z) H 3(z) H 1 H 2 H 3 H 4(z) DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 4

Filter Banks Introduction Step-2: Decimators (downsamplers) - To increase efficiency, subband sampling rate is reduced by factor N (= Nyquist (bandpass) sampling theorem, see Lecture-7) - Maximally decimated filter banks (=critically downsampled): N=M # subband samples= # fullband samples this sounds like maximum efficiency, but aliasing (see below)! - Oversampled filter banks (=non-critically downsampled): N<M # subband samples> # fullband samples M=4 H 1(z) IN H 2(z) H 3(z) H 4(z) DSP-II N=3 3 3 Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 5

Filter Banks Introduction Step-3: Subband processing - Example : coding (=compression) + (transmission or storage) + decoding - Filter bank design mostly assumes subband processing has `unit transfer function’ (output signals=input signals), i. e. mostly ignores presence of subband processing M=4 H 1(z) IN H 2(z) H 3(z) H 4(z) DSP-II N=3 3 3 subband processing Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 6

Filter Banks Introduction Step-4: Expanders (upsamplers) - restore original fullband sampling rate by N-fold upsampling (=insert N-1 zeros in between every two samples) M=4 H 1(z) IN H 2(z) H 3(z) H 4(z) DSP-II N=3 3 3 subband processing Version 2009 -2010 3 3 Lecture-6: Filter Banks - Preliminaries p. 7

Filter Banks Introduction Step-5: Synthesis filter bank - upsampling has to be followed by (interpolation) filtering (see below) - collection of M `synthesis’ (`interpolation’) filters, with a `common’ (summed) output signal - frequency responses : preferably `matched’ to frequency responses of the analysis filters, e. g. , to provide perfect reconstruction (see below) G 1 M=4 H 1(z) IN H 2(z) H 3(z) H 4(z) DSP-II G 3 G 4 N=3 3 3 G 2 subband processing Version 2009 -2010 3 3 G 1(z) G 2(z) G 3(z) OUT + G 4(z) Lecture-6: Filter Banks - Preliminaries p. 8

Aliasing versus Perfect Reconstruction - Assume subband processing does not modify subband signals (e. g. lossless coding/decoding) -The overall aim would be to have y[k]=u[k-d], i. e. that the output signal is equal to the input signal up to a certain delay -But: downsampling introduces ALIASING, especially so in maximally decimated (but also in non-maximally decimated) filter banks (see also Lecture-7) M=4 H 1(z) u[k] H 2(z) H 3(z) H 4(z) DSP-II N=3 3 3 output = input Version 2009 -2010 3 3 G 1(z) G 2(z) G 3(z) y[k]=u[k-d]? + G 4(z) Lecture-6: Filter Banks - Preliminaries p. 9

Aliasing versus Perfect Reconstruction Question : Can y[k]=u[k-d] be achieved in the presence of aliasing ? Answer : YES !! PERFECT RECONSTRUCTION banks with synthesis bank designed to remove aliasing effects ! M=4 H 1(z) u[k] H 2(z) H 3(z) H 4(z) DSP-II N=3 3 3 output = input Version 2009 -2010 3 3 G 1(z) G 2(z) G 3(z) y[k]=u[k-d]? + G 4(z) Lecture-6: Filter Banks - Preliminaries p. 10

Filter Banks Applications • Subband coding : Coding = Fullband signal split into subbands & downsampled subband signals separately encoded (e. g. subband with smaller energy content encoded with fewer bits) Decoding = reconstruction of subband signals, then fullband signal synthesis (expanders + synthesis filters) Example : Image coding (e. g. wavelet filter banks) Example : Audio coding e. g. digital compact cassette (DCC), Mini. Disc, MPEG, . . . Filter bandwidths and bit allocations chosen to further exploit perceptual properties of human hearing (perceptual coding, masking, etc. ) DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 11

Filter Banks Applications • Subband adaptive filtering : - See Part III - Example : Acoustic echo cancellation Adaptive filter models (time-varying) acoustic echo path and produces a copy of the echo, which is then subtracted from microphone signal. = difficult problem ! * long acoustic impulse responses * time-varying DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 12

Filter Banks Applications • Subband adaptive filtering (continued): - Subband filtering = M (simpler? ) subband modeling problems instead of one (more complicated? ) fullband modeling problem - Perfect reconstruction guarantees distortion-free desired near-end speech signal H 1(z) H 2(z) H 3(z) H 4(z) DSP-II 3 3 3 3 ad. filter Version 2009 -2010 + + 3 3 G 1(z) G 2(z) G 3(z) OUT + G 4(z) Lecture-6: Filter Banks - Preliminaries p. 13

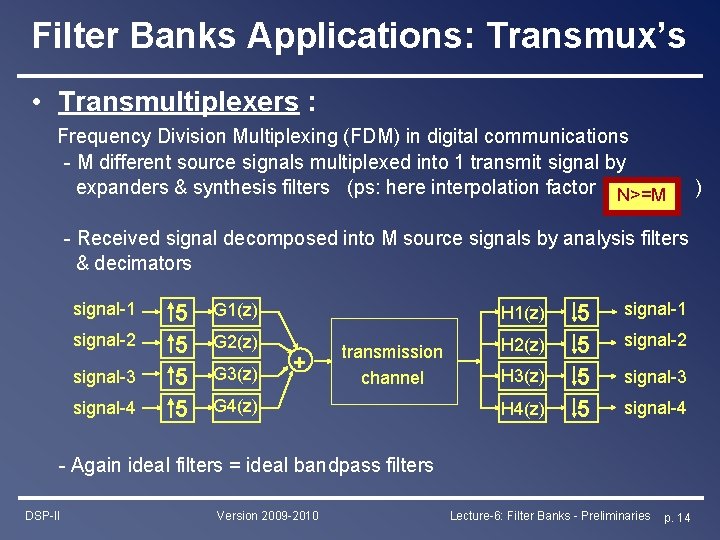
Filter Banks Applications: Transmux’s • Transmultiplexers : Frequency Division Multiplexing (FDM) in digital communications - M different source signals multiplexed into 1 transmit signal by expanders & synthesis filters (ps: here interpolation factor N>=M - Received signal decomposed into M source signals by analysis filters & decimators signal-1 signal-2 signal-3 signal-4 5 5 G 1(z) G 2(z) G 3(z) H 1(z) + transmission channel G 4(z) H 2(z) H 3(z) H 4(z) 5 5 signal-1 signal-2 signal-3 signal-4 - Again ideal filters = ideal bandpass filters DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 14 )

Filter Banks Applications: Transmux’s • Transmultiplexers : (continued) - Non-ideal synthesis & analysis filters result in aliasing and distortion, as well as CROSS-TALK between channels, i. e. each reconstructed signal contains unwanted contributions from other signals - Analysis & synthesis are reversed here, but similar perfect reconstruction theory (try it!) (where analysis bank removes cross-talk introduced by synthesis bank, if transmission channel = distortion free) DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 15

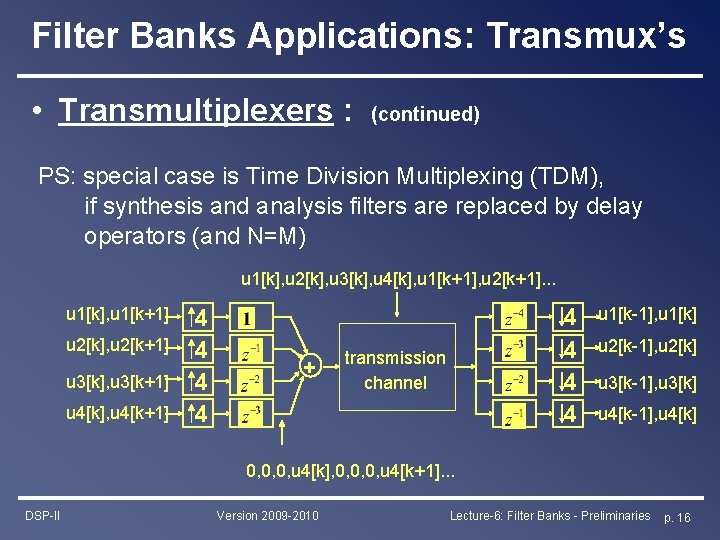
Filter Banks Applications: Transmux’s • Transmultiplexers : (continued) PS: special case is Time Division Multiplexing (TDM), if synthesis and analysis filters are replaced by delay operators (and N=M) u 1[k], u 2[k], u 3[k], u 4[k], u 1[k+1], u 2[k+1]. . . u 1[k], u 1[k+1] u 2[k], u 2[k+1] u 3[k], u 3[k+1] u 4[k], u 4[k+1] 4 4 + 4 4 transmission channel u 1[k-1], u 1[k] u 2[k-1], u 2[k] u 3[k-1], u 3[k] u 4[k-1], u 4[k] 0, 0, 0, u 4[k], 0, 0, 0, u 4[k+1]. . . DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 16

Sk Filter Banks Applications: Transmux’s ip th • Transmultiplexers : is (continued) sli de PS : special case is Code Division Multiple Access (CDMA), where filter coefficients=(orthogonal) user codes CDMA basics: (see digital coms courses)…… -Each user (i) is assigned a length-N pseudo-random code sequence -Transmission : For each symbol `chip’ sequence is transmitted (k-th symbol for user-i), a -Mostly binary codes ( ) with BPSK/QPSK symbols -Multiple access based on code-orthogonality (see below) DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 17

Sk Filter Banks Applications: Transmux’s ip th is CDMA basics: sli de -Reception : If (x) received signal = transmitted chip sequence (i. e. no channel effect, no noise), multiply chips with (synchronized) code sequence + sum. -Example (user i) transmitted symbols +1……… -1……… +1……… code sequence +1, -1, -1 transmitted chips +1, -1, -1, +1, +1, -1 received chips +1, -1, -1, +1, +1, -1, -1 (mult. with code & sum) received symbols (*1/4) +1………… -1……. …. . -1…………+1 (x) PS: real-world CDMA is considerably more complicated (different channels for different users + channel dispersion, asynchronous users, scrambling codes, etc. ) DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 18

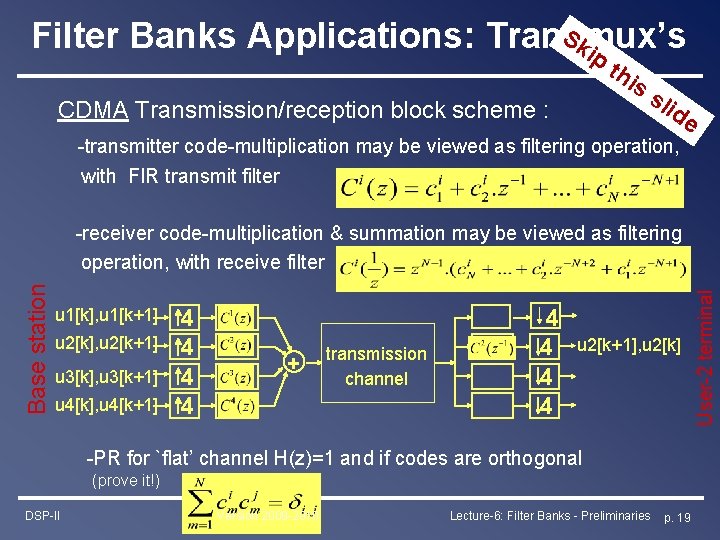
Sk Filter Banks Applications: Transmux’s ip th is CDMA Transmission/reception block scheme : sli de -transmitter code-multiplication may be viewed as filtering operation, with FIR transmit filter u 1[k], u 1[k+1] u 2[k], u 2[k+1] u 3[k], u 3[k+1] u 4[k], u 4[k+1] 4 4 + transmission channel 4 4 u 2[k+1], u 2[k] -PR for `flat’ channel H(z)=1 and if codes are orthogonal (prove it!) DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 19 User-2 terminal Base station -receiver code-multiplication & summation may be viewed as filtering operation, with receive filter

PR-FB Example: DFT/IDFT Filter Bank • Fundamental question is. . : Downsampling introduces ALIASING, then how can PERFECT RECONSTRUCTION (PR) (i. e. y[k]=u[k-d]) be achieved ? • Next slides provide simple PR-FB examples, to demonstrate that PR can indeed (easily) be obtained • Discover the magic of aliasing-compensation…. H 1(z) u[k] H 2(z) H 3(z) H 4(z) DSP-II 4 4 output = input Version 2009 -2010 4 4 G 1(z) G 2(z) G 3(z) y[k]=u[k-d]? + G 4(z) Lecture-6: Filter Banks - Preliminaries p. 20

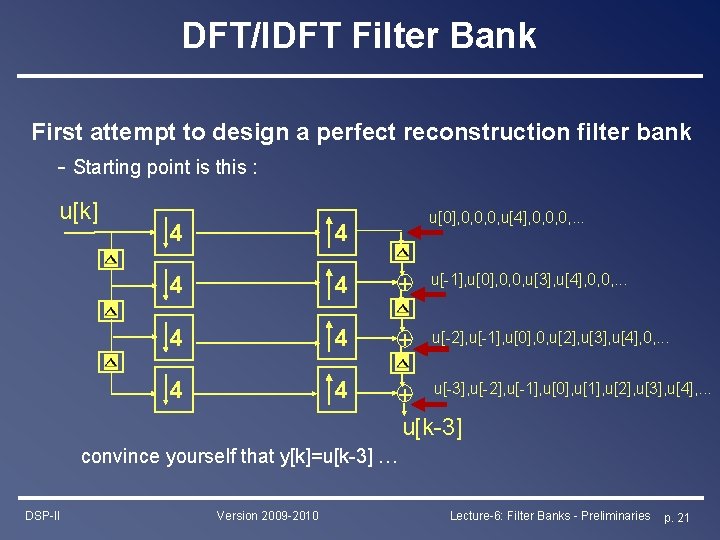
DFT/IDFT Filter Bank First attempt to design a perfect reconstruction filter bank - Starting point is this : u[k] u[0], 0, 0, 0, u[4], 0, 0, 0, . . . 4 4 + u[-1], u[0], 0, 0, u[3], u[4], 0, 0, . . . 4 4 + u[-2], u[-1], u[0], 0, u[2], u[3], u[4], 0, . . . 4 4 + u[-3], u[-2], u[-1], u[0], u[1], u[2], u[3], u[4], . . . u[k-3] convince yourself that y[k]=u[k-3] … DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 21

DFT/IDFT Filter Bank - An equivalent representation is. . . u[k] 4 4 4 4 + u[k-3] As y[k]=u[k-d], this can already be viewed as a perfect reconstruction filter bank (with aliasing in the subbands!) All analysis/synthesis filters are seen to be pure delays, hence are not frequency selective (i. e. far from ideal case with ideal bandpass filters…. ) ps: transmux version see p. 16 DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 22

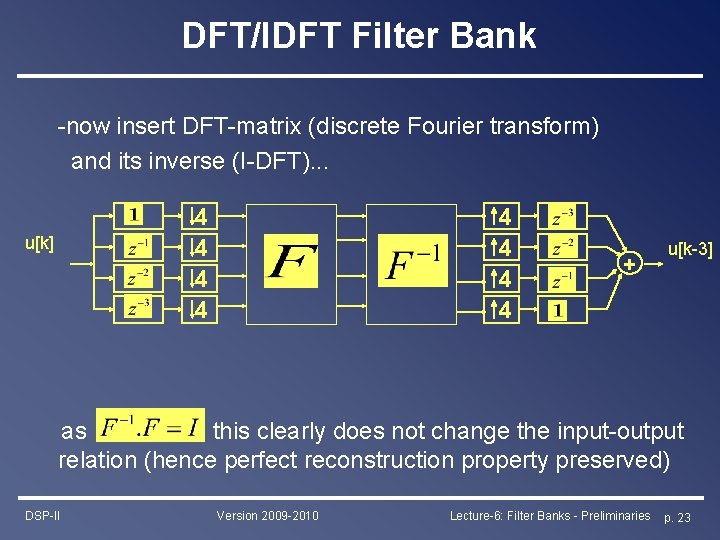
DFT/IDFT Filter Bank -now insert DFT-matrix (discrete Fourier transform) and its inverse (I-DFT). . . 4 4 u[k] 4 4 + u[k-3] as this clearly does not change the input-output relation (hence perfect reconstruction property preserved) DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 23

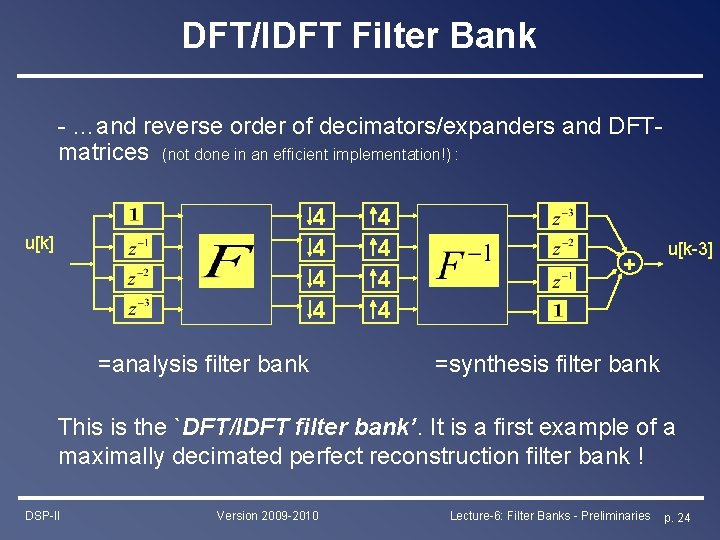
DFT/IDFT Filter Bank - …and reverse order of decimators/expanders and DFTmatrices (not done in an efficient implementation!) : 4 4 u[k] =analysis filter bank 4 4 + u[k-3] =synthesis filter bank This is the `DFT/IDFT filter bank’. It is a first example of a maximally decimated perfect reconstruction filter bank ! DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 24

DFT/IDFT Filter Bank What do analysis filters look like? u[k] This is seen (known) to represent a collection of filters Ho(z), H 1(z), . . . , each of which is a frequency shifted version of Ho(z) : i. e. the Hi are obtained by uniformly shifting the `prototype’ Ho over the frequency axis. DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 25

DFT/IDFT Filter Bank H 1(z) Ho(z) The prototype filter Ho(z) is a not-so-great lowpass filter with first sidelobe only 13 d. B below the main lobe. Ho(z) and Hi(z)’s are thus far from ideal lowpass/ bandpass filters. Hence (maximal) decimation introduces significant ALIASING in the decimated subband signals Still, we know this is a PERFECT RECONSTRUCTION filter bank (see construction p. 21 -24), which means the synthesis filters can apparently restore the aliasing distortion. This is remarkable! Other perfect reconstruction banks : see Lecture-7 DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 26

DFT/IDFT Filter Bank What do synthesis filters look like? *(1/N) + synthesis filters are (roughly) equal to analysis filters (details omitted, see also Lecture-7) PS: Efficient DFT/IDFT implementation based on FFT algorithm (`Fast Fourier Transform’). DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 27

Conclusions • Seen the general subband processing set-up + applications • Filter bank system is multi-rate structure, with decimators and expanders, hence ALIASING is a major concern • Seen a first (simple & not-so-great) example of a PERFECT RECONSTRUCTION filter bank (DFT/IDFT) • Sequel = other (better) PR structures Lecture 7: Maximally decimated filter banks Lecture 8: Modulated filter banks Lecture 9: Oversampled filter banks, etc. . • Reference: `Multirate Systems & Filter Banks’ , P. P. Vaidyanathan Prentice Hall 1993. DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 28

Review of Multi-rate Systems 1/10 • Decimation : decimator (downsampler) u[0], u[1], u[2]. . . N u[0], u[N], u[2 N]. . . example : u[k]: 1, 2, 3, 4, 5, 6, 7, 8, 9, … 2 -fold downsampling: 1, 3, 5, 7, 9, . . . • Interpolation : expander (upsampler) u[0], u[1], u[2], . . . N u[0], 0, . . 0, u[1], 0, …, 0, u[2]. . . example : u[k]: 1, 2, 3, 4, 5, 6, 7, 8, 9, … 2 -fold upsampling: 1, 0, 2, 0, 3, 0, 4, 0, 5, 0. . . DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 29

Review of Multi-rate Systems 2/10 • Z-transform (frequency domain) analysis of expander u[0], u[1], u[2], . . . N u[0], 0, . . 0, u[1], 0, …, 0, u[2]. . . N `images’ 3 `expansion in time domain ~ compression in frequency domain’ DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 30

Review of Multi-rate Systems 2 bis/10 • Z-transform (frequency domain) analysis of expander u[0], u[1], u[2], . . . N u[0], 0, . . 0, u[1], 0, …, 0, u[2]. . . expander mostly followed by `interpolation filter’ to remove images (and `interpolate the zeros) `images’ 3 LP interpolation filter can be low-/band-/high-pass (see Lecture-7) DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 31

Review of Multi-rate Systems 3/10 • Z-transform (frequency domain) analysis of decimator u[0], u[1], u[2]. . . N u[0], u[N], u[2 N]. . . N i=2 i=0 i=1 3 `compression in time domain ~ expansion in frequency domain’ DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 32

Review of Multi-rate Systems 3 bis/10 • Z-transform (frequency domain) analysis of decimator u[0], u[1], u[2]. . . N u[0], u[N], u[2 N]. . . decimation introduces ALIASING if input signal occupies frequency band larger than , hence mostly preceded by anti-aliasing (decimation) filter i=2 i=0 i=1 3 LP anti-aliasing filter can be low-/band-/high-pass (see Lecture-7) DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 33

Review of Multi-rate Systems 4/10 • Z-transform analysis of decimator (continued) N - Note that while is periodic with period the summation with i=0…N-1 restores the periodicity with period - Example: DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries ! p. 34

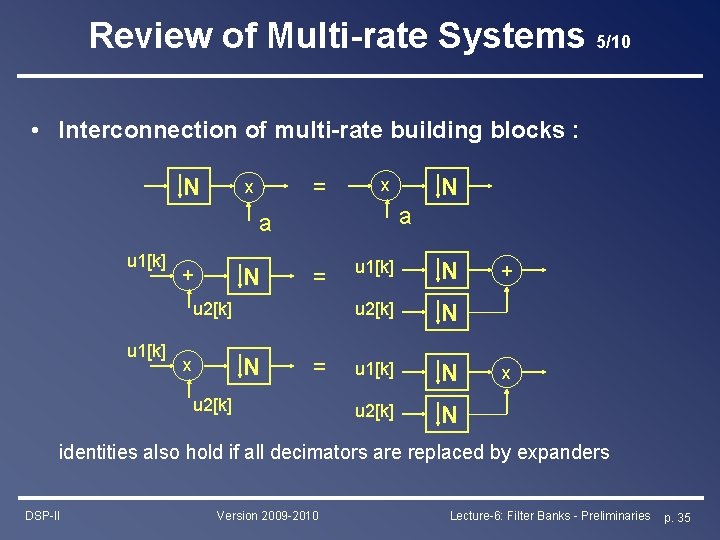
Review of Multi-rate Systems 5/10 • Interconnection of multi-rate building blocks : N = x a a u 1[k] N + = u 2[k] u 1[k] N x = u 2[k] u 1[k] N u 2[k] N + x identities also hold if all decimators are replaced by expanders DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 35

Review of Multi-rate Systems 6/10 • `Noble identities’ (I) : u[k] N y[k] (only for rational functions) = u[k] N y[k] Example : N=2 h[0], h[1], 0, 0, 0, … DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 36

Review of Multi-rate Systems 7/10 • `Noble identities’ (II) : u[k] N y[k] (only for rational functions) = u[k] N y[k] Example : N=2 h[0], h[1], 0, 0, 0, … DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 37

Review of Multi-rate Systems 8/10 Application of `noble identities : efficient multi-rate realizations of FIR filters through… • Polyphase decomposition: example : (2 -fold decomposition) example : (3 -fold decomposition) general: (N-fold decomposition) DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 38

Review of Multi-rate Systems 9/10 • Polyphase decomposition: Example : efficient implementation of an FIR decimation filter u[k] H(z) + = u[k] 2 2 2 + i. e. all filter operations performed at the lowest rate DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 39

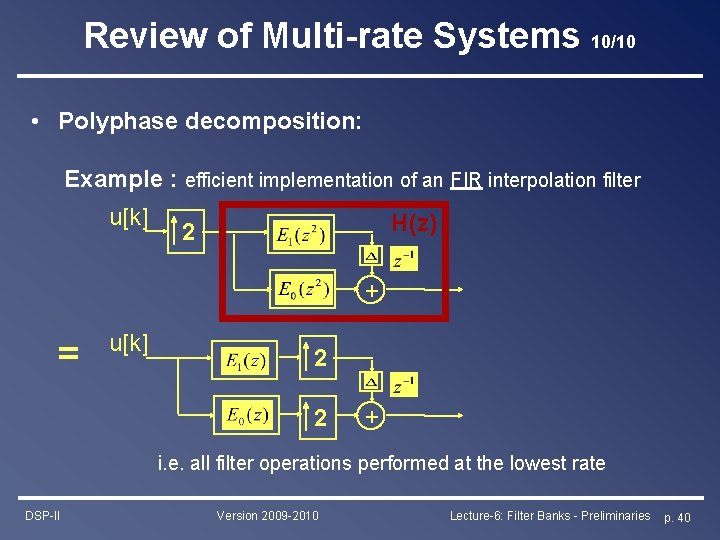
Review of Multi-rate Systems 10/10 • Polyphase decomposition: Example : efficient implementation of an FIR interpolation filter u[k] H(z) 2 + = u[k] 2 2 + i. e. all filter operations performed at the lowest rate DSP-II Version 2009 -2010 Lecture-6: Filter Banks - Preliminaries p. 40