Digital Signal Processing II Lecture 5 Filter Banks

Digital Signal Processing II Lecture 5: Filter Banks - Preliminaries Marc Moonen Dept. E. E. /ESAT, K. U. Leuven marc. moonen@esat. kuleuven. be homes. esat. kuleuven. be/~moonen/ DSP-II p. 1

Part-II : Filter Banks Lecture-5 : Preliminaries • Applications • Intro perfect reconstruction filter banks (PR FBs) Lecture-6 : Maximally decimated FBs • Multi-rate systems review • PR FBs • Paraunitary PR FBs Lecture-7 : Modulated FBs • DFT-modulated FBs • Cosine-modulated FBs Lecture-8 DSP-II : Special Topics • Non-uniform FBs & Wavelets • Oversampled DFT-modulated FBs • Frequency domain filtering Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 2

PART-II : Filter Banks LECTURE-5 : Filter Banks Preliminaries • • Filter banks introduction Aliasing vs. perfect reconstruction (PR) Filter banks applications 1 st PR FB example : DFT/IDFT filter bank DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 3
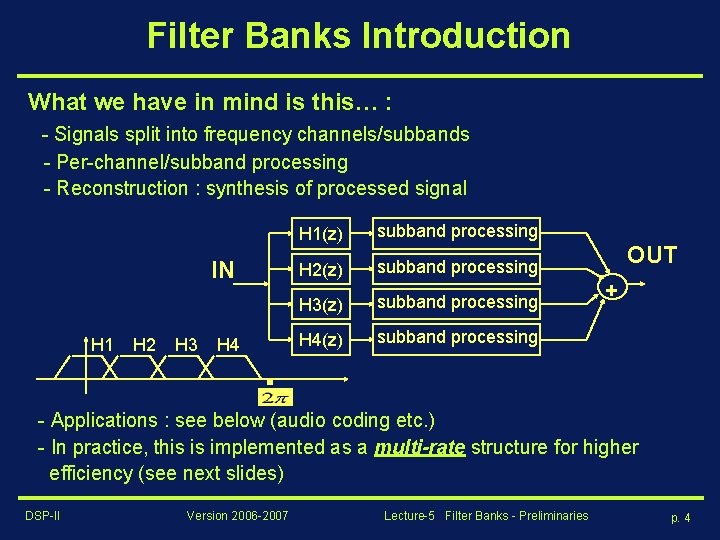
Filter Banks Introduction What we have in mind is this… : - Signals split into frequency channels/subbands - Per-channel/subband processing - Reconstruction : synthesis of processed signal IN H 1 H 2 H 3 H 4 H 1(z) subband processing H 2(z) subband processing H 3(z) subband processing H 4(z) subband processing OUT + - Applications : see below (audio coding etc. ) - In practice, this is implemented as a multi-rate structure for higher efficiency (see next slides) DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 4

Filter Banks Introduction Step-1: Analysis filter bank - collection of M filters (`analysis filters’, `decimation filters’) with a common input signal - ideal (but non-practical) frequency responses = ideal bandpass filters - typical frequency responses (overlapping, marginally overlapping, non-overlapping) M=4 H 1(z) IN H 2(z) H 3(z) H 1 H 2 H 3 H 4(z) DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 5

Filter Banks Introduction Step-2: Decimators (downsamplers) - To increase efficiency, subband sampling rate can be reduced by factor N (cfr. Nyquist theorem). - maximally decimated filter banks (=critically downsampled filter banks): hence # subband samples= # fullband N=M samples this sounds like maximum efficiency, but aliasing (see below)! - oversampled filter banks (=non-critically downsampled filter banks): N<M hence # subband samples> # fullband samples M=4 N=3 H 1(z) IN H 2(z) H 3(z) H 4(z) DSP-II 3 3 Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 6

Filter Banks Introduction Step-3: Subband processing - Example : coding (=compression) + (transmission or storage) + decoding - Filter bank design mostly assumes subband processing has `unit transfer function’ (output signals=input signals), i. e. mostly ignores presence of subband processing IN DSP-II M=4 N=3 H 1(z) 3 subband processing H 2(z) 3 subband processing H 3(z) 3 subband processing H 4(z) 3 subband processing Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 7
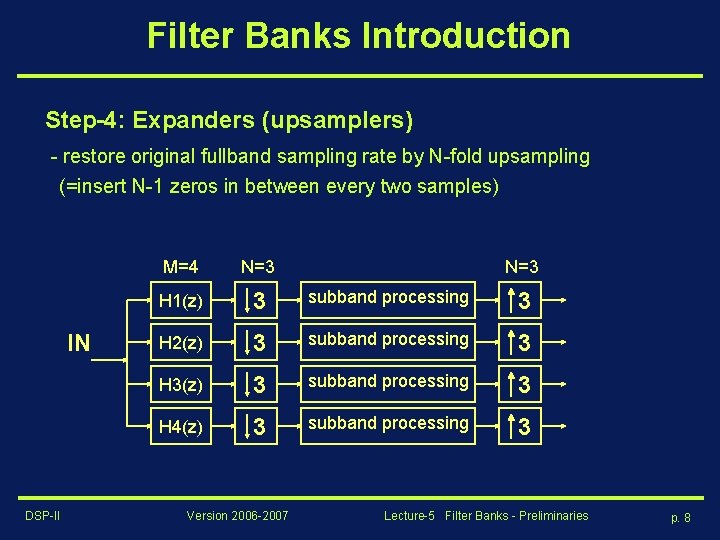
Filter Banks Introduction Step-4: Expanders (upsamplers) - restore original fullband sampling rate by N-fold upsampling (=insert N-1 zeros in between every two samples) IN DSP-II M=4 N=3 H 1(z) 3 subband processing 3 H 2(z) 3 subband processing 3 H 3(z) 3 subband processing 3 H 4(z) 3 subband processing 3 Version 2006 -2007 N=3 Lecture-5 Filter Banks - Preliminaries p. 8

Filter Banks Introduction Step-5: Synthesis filter bank - upsampling has to be followed by (interpolation) filtering (see below p. 31) - collection of M `synthesis’ (`interpolation’) filters, with a `common’ (summed) output signal - frequency responses : preferably `matched’ to frequency responses of the analysis filters, e. g. , to provide perfect reconstruction (see below) M=4 H 1(z) IN H 2(z) H 3(z) H 4(z) N=3 3 3 3 3 subband processing G 1 DSP-II Version 2006 -2007 G 2 G 1(z) G 2(z) G 3(z) OUT + G 4(z) G 3 G 4 Lecture-5 Filter Banks - Preliminaries p. 9
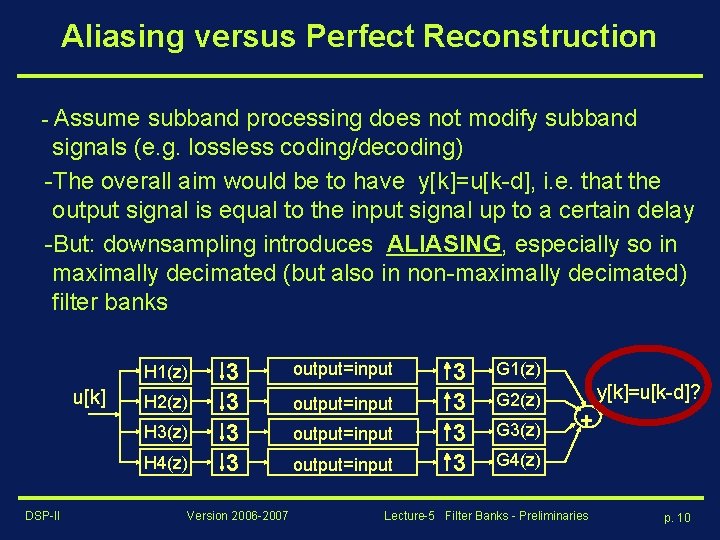
Aliasing versus Perfect Reconstruction - Assume subband processing does not modify subband signals (e. g. lossless coding/decoding) -The overall aim would be to have y[k]=u[k-d], i. e. that the output signal is equal to the input signal up to a certain delay -But: downsampling introduces ALIASING, especially so in maximally decimated (but also in non-maximally decimated) filter banks H 1(z) u[k] H 2(z) H 3(z) H 4(z) DSP-II 3 3 Version 2006 -2007 output=input 3 3 G 1(z) G 2(z) G 3(z) y[k]=u[k-d]? + G 4(z) Lecture-5 Filter Banks - Preliminaries p. 10
![Aliasing versus Perfect Reconstruction Question : Can y[k]=u[k-d] be achieved in the presence of Aliasing versus Perfect Reconstruction Question : Can y[k]=u[k-d] be achieved in the presence of](http://slidetodoc.com/presentation_image_h/0a11d3b125ea726d53fee49a9cca7b86/image-11.jpg)
Aliasing versus Perfect Reconstruction Question : Can y[k]=u[k-d] be achieved in the presence of aliasing ? Answer : YES !! PERFECT RECONSTRUCTION banks with synthesis bank designed to remove aliasing effects ! H 1(z) u[k] H 2(z) H 3(z) H 4(z) DSP-II 3 3 Version 2006 -2007 output=input 3 3 G 1(z) G 2(z) G 3(z) y[k]=u[k-d]? + G 4(z) Lecture-5 Filter Banks - Preliminaries p. 11

Filter Banks Applications • Subband coding : Coding = Fullband signal split into subbands & downsampled subband signals separately encoded (e. g. subband with smaller energy content encoded with fewer bits) Decoding = reconstruction of subband signals, then fullband signal synthesis (expanders + synthesis filters) Example : Image coding (e. g. wavelet filter banks) Example : Audio coding e. g. digital compact cassette (DCC), Mini. Disc, MPEG, . . . Filter bandwidths and bit allocations chosen to further exploit perceptual properties of human hearing (perceptual coding, masking, etc. ) DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 12

Filter Banks Applications • Subband adaptive filtering : - See Part III - Example : Acoustic echo cancellation Adaptive filter models (time-varying) acoustic echo path and produces a copy of the echo, which is then subtracted from microphone signal. = difficult problem ! *long acoustic impulse responses *time-varying DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 13
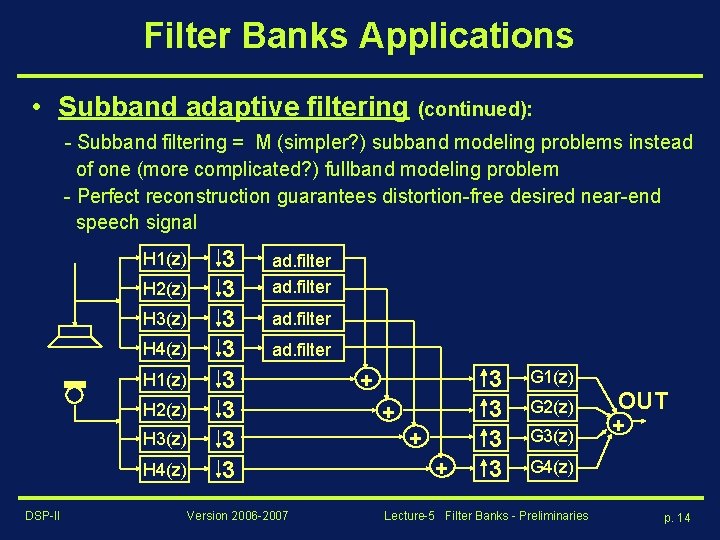
Filter Banks Applications • Subband adaptive filtering (continued): - Subband filtering = M (simpler? ) subband modeling problems instead of one (more complicated? ) fullband modeling problem - Perfect reconstruction guarantees distortion-free desired near-end speech signal H 1(z) H 2(z) H 3(z) H 4(z) DSP-II 3 3 3 3 ad. filter Version 2006 -2007 + + 3 3 G 1(z) G 2(z) G 3(z) OUT + G 4(z) Lecture-5 Filter Banks - Preliminaries p. 14
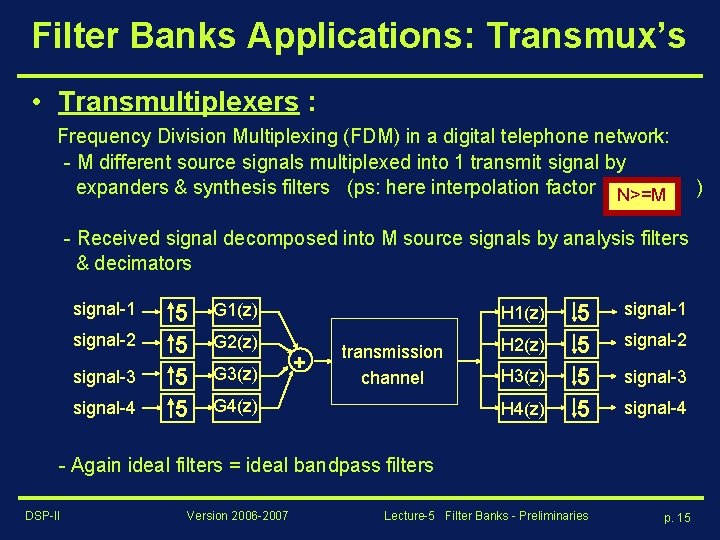
Filter Banks Applications: Transmux’s • Transmultiplexers : Frequency Division Multiplexing (FDM) in a digital telephone network: - M different source signals multiplexed into 1 transmit signal by expanders & synthesis filters (ps: here interpolation factor N>=M - Received signal decomposed into M source signals by analysis filters & decimators signal-1 signal-2 signal-3 signal-4 5 5 G 1(z) G 2(z) G 3(z) H 1(z) + transmission channel G 4(z) H 2(z) H 3(z) H 4(z) 5 5 signal-1 signal-2 signal-3 signal-4 - Again ideal filters = ideal bandpass filters DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 15 )

Filter Banks Applications: Transmux’s • Transmultiplexers : (continued) - Non-ideal synthesis & analysis filters result in CROSS-TALK between channels, i. e. each reconstructed signal contains unwanted contributions from other signals - Analysis & synthesis are reversed here, but similar perfect reconstruction theory (try it!) (where analysis bank removes cross-talk introduced by synthesis bank, if transmission channel = distortion free) DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 16
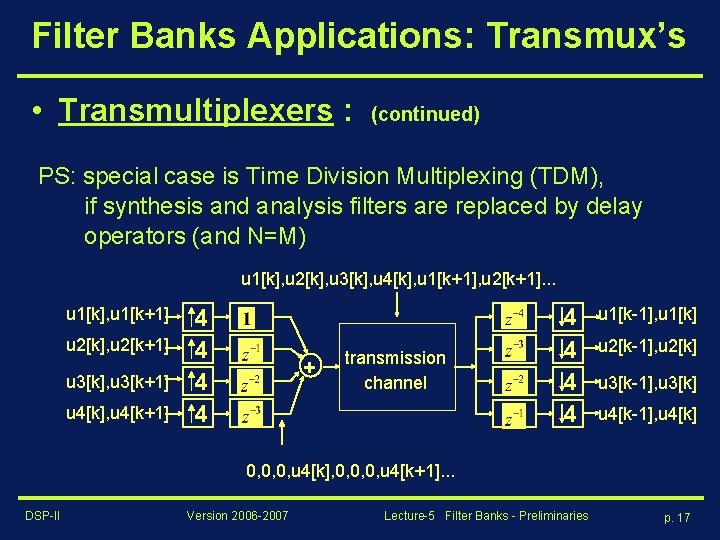
Filter Banks Applications: Transmux’s • Transmultiplexers : (continued) PS: special case is Time Division Multiplexing (TDM), if synthesis and analysis filters are replaced by delay operators (and N=M) u 1[k], u 2[k], u 3[k], u 4[k], u 1[k+1], u 2[k+1]. . . u 1[k], u 1[k+1] u 2[k], u 2[k+1] u 3[k], u 3[k+1] u 4[k], u 4[k+1] 4 4 + transmission channel 4 4 u 1[k-1], u 1[k] u 2[k-1], u 2[k] u 3[k-1], u 3[k] u 4[k-1], u 4[k] 0, 0, 0, u 4[k], 0, 0, 0, u 4[k+1]. . . DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 17

Filter Banks Applications: Transmux’s • Transmultiplexers : (continued) PS : special case is Code Division Multiple Access (CDMA), where filter coefficients=(orthogonal) user codes CDMA basics: (see digital coms courses)…… -Each user-i is assigned a pseudo-random code sequence -Transmission : For each symbol `chip’ sequence is transmitted (k-th symbol for user-i), a -Mostly binary codes ( ) with BPSK/QPSK symbols -Multiple access based on code-orthogonality (see below) DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 18

Filter Banks Applications: Transmux’s CDMA basics: -Reception : If received signal = transmitted chip sequence (i. e. no channel effect, no noise), multiply chips with (synchronized) code sequence + sum. -Example (user i) transmitted symbols +1……… -1……… +1……… code sequence +1, -1, -1 transmitted chips +1, -1, -1, +1, +1, -1, -1 received chips +1, -1, -1, +1, +1, -1, -1 (mult. with code & sum) received symbols (*1/4) +1………… -1……. …. . -1…………+1 DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 19
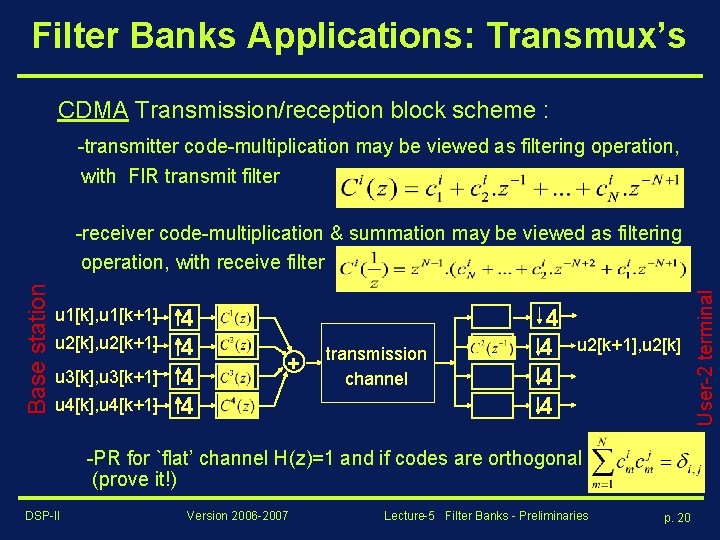
Filter Banks Applications: Transmux’s CDMA Transmission/reception block scheme : -transmitter code-multiplication may be viewed as filtering operation, with FIR transmit filter u 1[k], u 1[k+1] u 2[k], u 2[k+1] u 3[k], u 3[k+1] u 4[k], u 4[k+1] 4 4 + transmission channel 4 4 u 2[k+1], u 2[k] -PR for `flat’ channel H(z)=1 and if codes are orthogonal (prove it!) DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 20 User-2 terminal Base station -receiver code-multiplication & summation may be viewed as filtering operation, with receive filter

Filter Bank Applications: Transmux’s CDMA • PS: real-world CDMA more complicated (different channels for different users + channel dispersion (instead of H(z)=1 for all users), asynchronous users, scrambling codes, etc. ) • PS: CDMA application examples : - IS-95 cellular telephony (Qualcomm) - UMTS (`wideband CDMA’) - IEEE 802. 11 wireless LANs - GPS - cable modems, power line comms, …. DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 21

PR-FB Example: DFT/IDFT Filter Bank • Fundamental question is. . : Downsampling introduces ALIASING , then how can PERFECT RECONSTRUCTION (PR) (i. e. y[k]=u[k-d]) be achieved ? • Next slides provide simple PR-FB examples, to demonstrate that PR can indeed (easily) be obtained • Discover the magic of aliasing-compensation…. DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 22
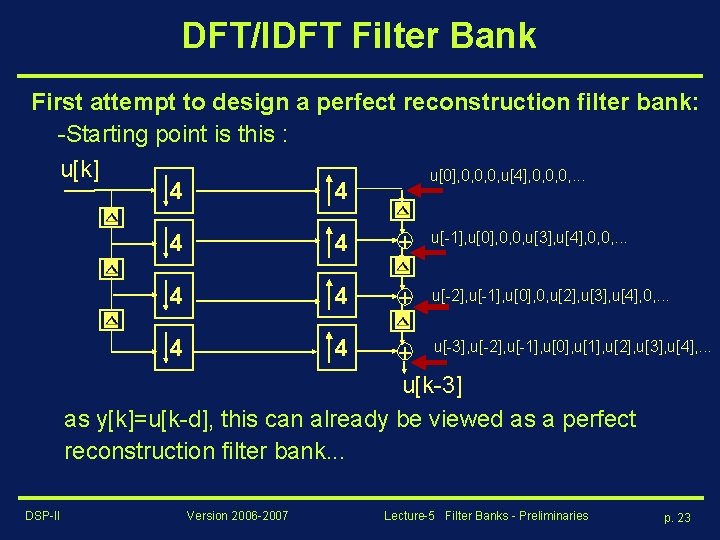
DFT/IDFT Filter Bank First attempt to design a perfect reconstruction filter bank: -Starting point is this : u[k] u[0], 0, 0, 0, u[4], 0, 0, 0, . . . 4 4 + u[-1], u[0], 0, 0, u[3], u[4], 0, 0, . . . 4 4 + u[-2], u[-1], u[0], 0, u[2], u[3], u[4], 0, . . . 4 4 + u[-3], u[-2], u[-1], u[0], u[1], u[2], u[3], u[4], . . . u[k-3] as y[k]=u[k-d], this can already be viewed as a perfect reconstruction filter bank. . . DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 23
![DFT/IDFT Filter Bank - An equivalent representation is. . . u[k] 4 4 4 DFT/IDFT Filter Bank - An equivalent representation is. . . u[k] 4 4 4](http://slidetodoc.com/presentation_image_h/0a11d3b125ea726d53fee49a9cca7b86/image-24.jpg)
DFT/IDFT Filter Bank - An equivalent representation is. . . u[k] 4 4 4 4 + u[k-3] All analysis/synthesis filters are seen to be pure delays, hence are not frequency selective (i. e. far from ideal case with ideal bandpass filters…. ) ps: transmux version see p. 17 DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 24
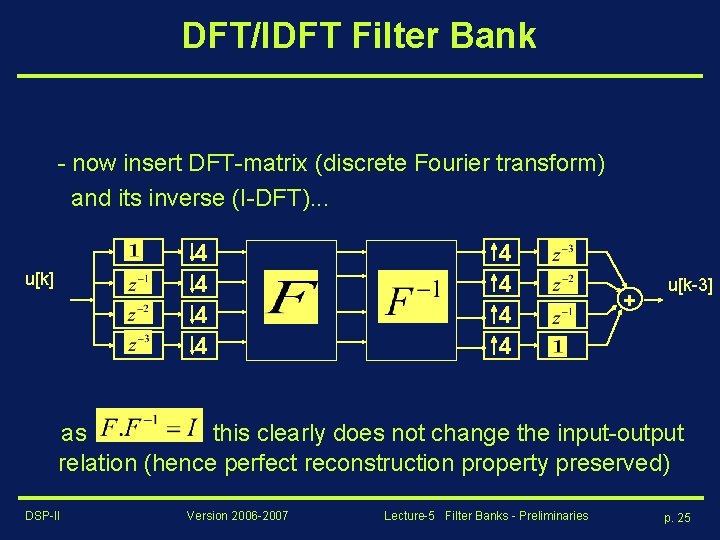
DFT/IDFT Filter Bank - now insert DFT-matrix (discrete Fourier transform) and its inverse (I-DFT). . . 4 4 u[k] 4 4 + u[k-3] as this clearly does not change the input-output relation (hence perfect reconstruction property preserved) DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 25
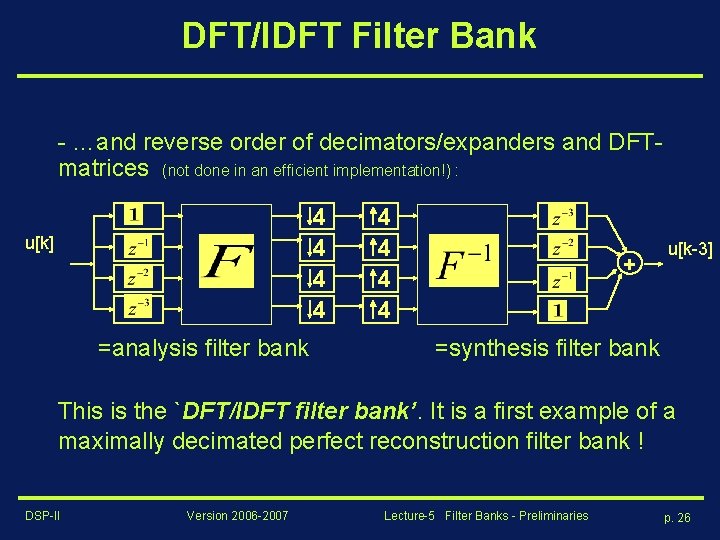
DFT/IDFT Filter Bank - …and reverse order of decimators/expanders and DFTmatrices (not done in an efficient implementation!) : 4 4 u[k] =analysis filter bank 4 4 + u[k-3] =synthesis filter bank This is the `DFT/IDFT filter bank’. It is a first example of a maximally decimated perfect reconstruction filter bank ! DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 26
![DFT/IDFT Filter Bank What do analysis filters look like? u[k] This is seen (known) DFT/IDFT Filter Bank What do analysis filters look like? u[k] This is seen (known)](http://slidetodoc.com/presentation_image_h/0a11d3b125ea726d53fee49a9cca7b86/image-27.jpg)
DFT/IDFT Filter Bank What do analysis filters look like? u[k] This is seen (known) to represent a collection of filters Ho(z), H 1(z), . . . , each of which is a frequency shifted version of Ho(z) : i. e. the Hi are obtained by uniformly shifting the `prototype’ Ho over the frequency axis. DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 27
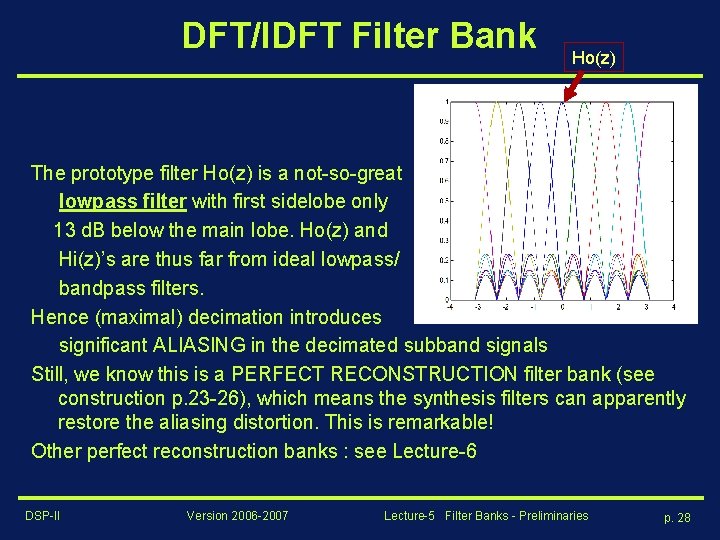
DFT/IDFT Filter Bank Ho(z) The prototype filter Ho(z) is a not-so-great lowpass filter with first sidelobe only 13 d. B below the main lobe. Ho(z) and Hi(z)’s are thus far from ideal lowpass/ bandpass filters. Hence (maximal) decimation introduces significant ALIASING in the decimated subband signals Still, we know this is a PERFECT RECONSTRUCTION filter bank (see construction p. 23 -26), which means the synthesis filters can apparently restore the aliasing distortion. This is remarkable! Other perfect reconstruction banks : see Lecture-6 DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 28

DFT/IDFT Filter Bank What do synthesis filters look like? + synthesis filters are (roughly) equal to analysis filters (details omitted, see also Lecture-6) PS: Efficient DFT/IDFT implementation based FFT algorithm (`Fast Fourier Transform’). In the sequel, every time a DFT (IDFT) matrix is shown, FFT (IFFT) -implementation is assumed. DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 29

Conclusions • Seen the general subband processing set-up + applications • Filter bank system is multi-rate structure, with decimators and expanders, hence ALIASING is a major concern • Seen a first (simple & not-so-great) example of a PERFECT RECONSTRUCTION filter bank (DFT/IDFT) • Sequel = other (better) PR structures Lecture 6: Maximally decimated filter banks Lecture 7: Modulated filter banks Lecture 8: Oversampled filter banks, etc. . • Reference: `Multirate Systems & Filter Banks’ , P. P. Vaidyanathan Prentice Hall 1993. DSP-II Version 2006 -2007 Lecture-5 Filter Banks - Preliminaries p. 30
- Slides: 30