Digital Signal Processing FIR Filter Design Marc Moonen

Digital Signal Processing FIR Filter Design Marc Moonen Dept. E. E. /ESAT, K. U. Leuven DSP-II p. 1

FIR Filter Design • Review of discrete-time systems LTI systems, impulse response, transfer function, . . . • FIR filters Direct form, Lattice, Linear-phase filters • FIR design by optimization Weighted least-squares design Minimax design • FIR design using `windows’ • Equiripple design • Software (Matlab, …)

Review of discrete-time systems 1/10 Linear time-invariant (LTI) systems u[k] y[k] • Linear : input u 1[k] -> output y 1[k] input u 2[k] -> output y 2[k] hence input a. u 1[k]+b. u 2[k]-> a. y 1[k]+b. y 2[k] • Time-invariant (shift-invariant) input u[k] -> output y[k] hence input u[k-T] -> output y[k-T]

Review of discrete-time systems 2/10 Linear time-invariant (LTI) systems u[k] • Causal systems: for all input u[k]=0, k<0 -> output y[k]=0, k<0 • Impulse response : input 1, 0, 0, 0, . . . -> output h[0], h[1], h[2], h[3], . . . input u[0], u[1], u[2], u[3] -> output y[0], y[1], y[2], y[3], . . . = `convolution’ y[k]

Review of discrete-time systems 3/10 • Impulse response/convolution: u[0], u[1], u[2], u[3], 0, 0…. y[0], y[1], . . . h[0], h[1], h[2], 0, 0, . . . `Toeplitz’ matrix

Review of discrete-time systems 4/10 • Z-Transform:

Review of discrete-time systems 5/10 Z-Transform : • input-output relation • `shorthand’ notation (for convolution operation/Toeplitz-vector product) • stability bounded input u[k] -> bounded output y[k] --iff poles of H(z) inside the unit circle (for causal, rational systems)

Review of discrete-time systems 6/10 Frequency response : • given a system with impulse response h[k] • given an input signal = complex sinusoid • output signal : is `frequency response’ is H(z) evaluated on the unit circle

Review of discrete-time systems 7/10 Frequency response : • for a real impulse response h[k] Magnitude response Phase response • example : is even function is odd function Nyquist frequency

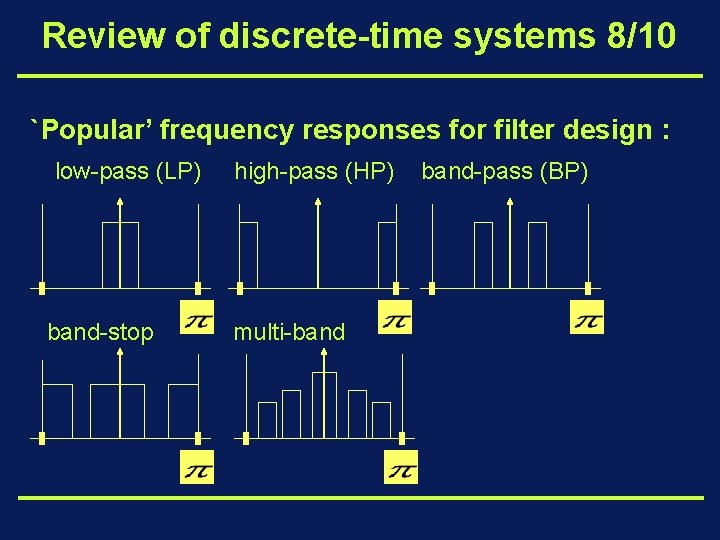
Review of discrete-time systems 8/10 `Popular’ frequency responses for filter design : low-pass (LP) band-stop high-pass (HP) multi-band-pass (BP)

Review of discrete-time systems 9/10 Rational transfer functions (`IIR filters’): • • N poles (zeros of A(z)) , N zeros (zeros of B(z)) • corresponds to difference equation

Review of discrete-time systems 10/10 `FIR filters’ (finite impulse response): • • • `Moving average filters’ (MA) N poles at the origin z=0 (hence guaranteed stability) N zeros (zeros of B(z)), `all zero’ filters corresponds to difference equation • impulse response

Review of discrete-time systems `FIR filter’ (finite impulse response) design • this lecture +++ : phase control (linear phase) guaranteed stability design flexibility minor coefficient sensitivity/quantization/round-off problems, …. - - - : long filters, hence expensive

FIR Filters 1/14 • `direct-form’ realization u[k] u[k-1] b 1 bo u[k-2] b 2 u[k-3] b 3 u[k-4] b 4 x x + + y[k] x

FIR Filters 2/14 • `retiming’ = select subgraph (shaded) remove delay element on all inbound arrows add delay element on all outbound arrows u[k] bo u[k-1] b 1 u[k-2] b 2 u[k-3] b 3 u[k-4] b 4 x x + + y[k] x

FIR Filters 3/14 • `retiming’ : results in. . . u[k] bo u[k-1] b 1 u[k-2] b 2 b 3 u[k-3] b 4 x x + + y[k] x

FIR Filters 4/14 • `retiming’ : repeated application results in. . . `Transposed direct-form’ realization u[k] b 1 bo b 2 b 3 b 4 x x + + y[k] x

FIR Filters 5/14 • `Lattice form’ : derived from combined realization with reversed coefficient vector results in - same magnitude response - different phase response

FIR Filters 6/14 • `Lattice form’ : derivation (I) u[k] bo x y[k] u[k-1] u[k-2] u[k-3] u[k-4] b 1 x b 2 x b 3 x b 4 x x b 3 x b 2 x b 4 x b 1 x bo + + + +

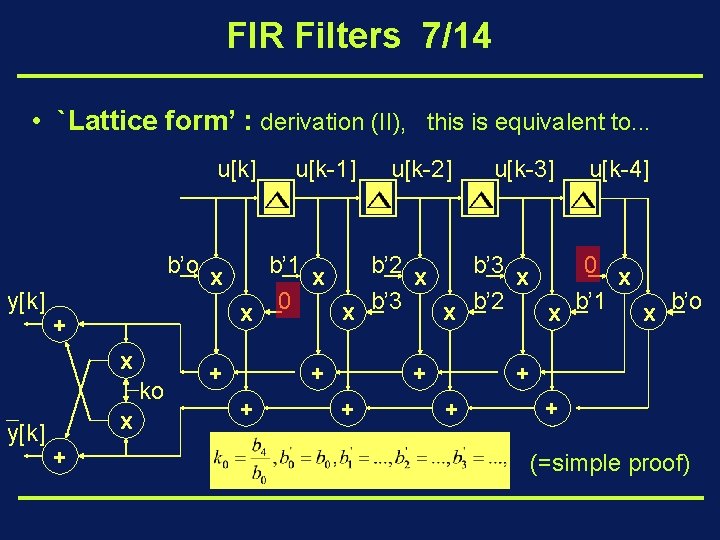
FIR Filters 7/14 • `Lattice form’ : derivation (II), this is equivalent to. . . u[k] y[k] b’o x + x ko y[k] x + u[k-1] u[k-2] u[k-3] u[k-4] b’ 1 x b’ 2 x b’ 3 x 0 x x b’ 3 x b’ 2 x 0 x b’ 1 x b’o + + + + (=simple proof)

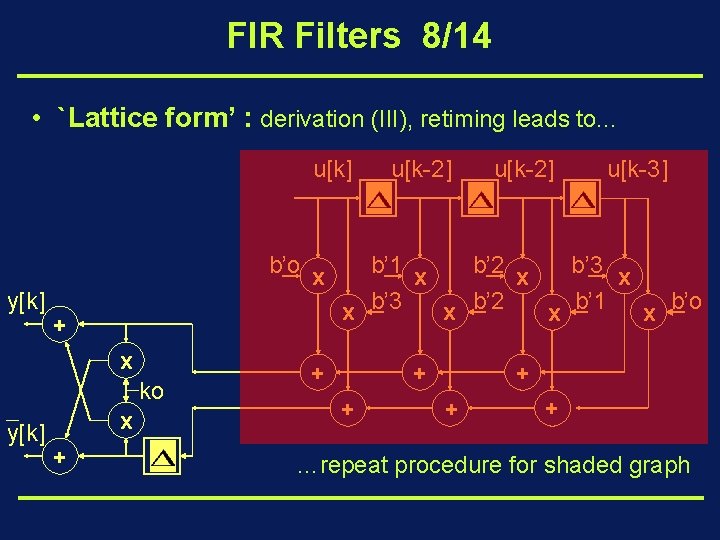
FIR Filters 8/14 • `Lattice form’ : derivation (III), retiming leads to. . . u[k] y[k] b’o x + x ko y[k] x + u[k-2] u[k-3] b’ 1 x b’ 2 x b’ 3 x b’ 2 x b’ 1 x b’o + + + …repeat procedure for shaded graph

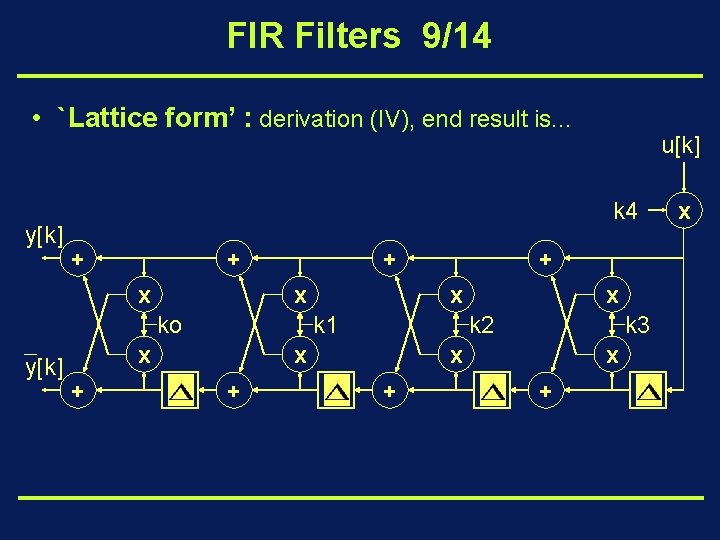
FIR Filters 9/14 • `Lattice form’ : derivation (IV), end result is. . . y[k] k 4 + + x ko y[k] u[k] x k 1 x + + k 2 x + x k 3 x + x

FIR Filters 10/14 `Lattice form’ : • ki’s are `reflection coefficients’ • procedure for computing ki’s from bi’s corresponds to `Schur-Cohn’ stability test (control theory): all zeros of B(z) are stable (i. e. lie inside unit circle) iff all reflection coefficients statisfy |ki|<1 (i=1, …, N-1) (ps: procedure breaks down if |ki|=1 is encountered)

FIR Filters 11/14 Linear-phase FIR filters • Non-causal zero-phase filters : example: symmetric impulse response h[-L], …. h[-1], h[0], h[1], . . . , h[L] h[k]=h[-k], k=1. . L frequency response is L k - real-valued (=zero-phase) transfer function - causal implementation by introducing (group) delay

FIR Filters 12/14 Linear-phase FIR filters • Causal linear-phase filters : example: symmetric impulse response & N even h[0], h[1], …. , h[N] N=2 L (even) h[k]=h[N-k], k=0. . L 0 N frequency response is - causal implementation of zero-phase filter, by introducing (group) delay k

FIR Filters 13/14 Linear-phase FIR filters Type-1 N=2 L=even symmetric h[k]=h[N-k] LP/HP/BP Type-2 N=2 L+1=odd anti-symmetric h[k]=-h[N-k] zero at LP/BP Type-2 N=2 L=even symmetric h[k]=h[N-k] zero at Type-4 N=2 L+1=odd anti-symmetric h[k]=-h[N-k] zero at HP

FIR Filters 14/14 Linear-phase FIR filters u[k] • efficient direct-form realization. example: + bo y[k] + + b 1 b 2 b 3 b 4 x x x + +

Filter Design by Optimization (I) Weighted Least Squares Design : • select one of the basic forms that yield linear phase e. g. Type-1 • specify desired frequency response (LP, HP, BP, …) e. g. : LP • optimization criterion is where is a weighting function

Filter Design by Optimization • …this is equivalent to i. e. convex `Quadratic Optimization’ problem • this is often supplemented with additional constraints. . .

Filter Design by Optimization Example: Low-pass (LP) design optimization criterion is an additional constraint may be imposed to control the pass -band ripple … … as well as the stop-band ripple

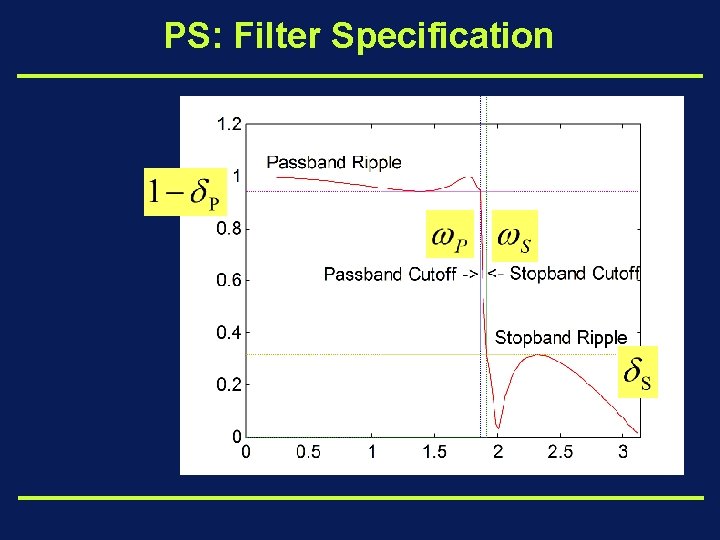
PS: Filter Specification

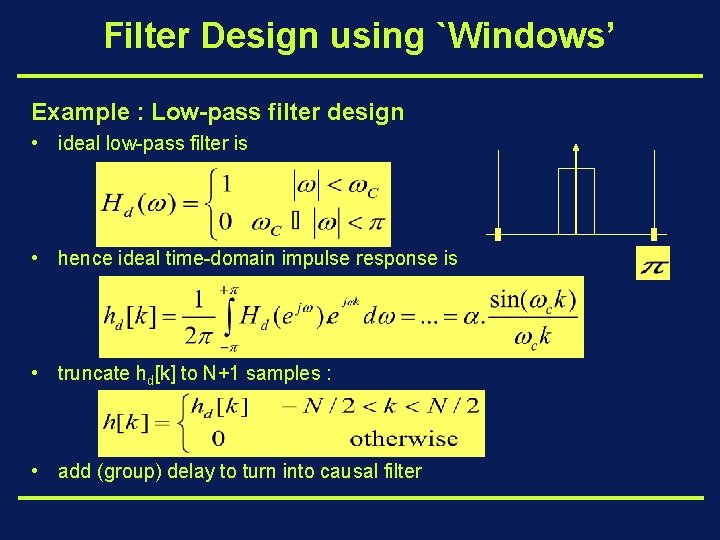
Filter Design using `Windows’ Example : Low-pass filter design • ideal low-pass filter is • hence ideal time-domain impulse response is • truncate hd[k] to N+1 samples : • add (group) delay to turn into causal filter

Filter Design using `Windows’ Example : Low-pass filter design (continued) • it can be shown that this corresponds to the solution of weighted leastsquares optimization with the given Hd, and weighting function for all freqs. • truncation corresponds to applying a `rectangular window’ : • +++: simple procedure (also for HP, BP, …) • - - - : truncation in the time-domain results in `Gibbs effect’ in the frequency domain, i. e. large ripple in pass-band stop-band, which cannot be reduced by increasing the filter order N.

Filter Design using `Windows’ Remedy : apply windows other than rectangular window: • time-domain multiplication with a window function w[k] corresponds to frequency domain convolution with W(z) : • candidate windows : Han, Hamming, Blackman, Kaiser, …. (see textbooks, see DSP-I) • window choice/design = trade-off between side-lobe levels (define peak pass-/stop-band ripple) and width main-lobe (defines transition bandwidth)

Design Procedure • To fully design and implement a filter five steps are required: (1) (2) (3) (4) (5) Filter specification. Coefficient calculation. Structure selection. Simulation (optional). Implementation.

Filter Specification - Step 1

Coefficient Calculation - Step 2 • There are several different methods available, the most popular are: – Window method. – Frequency sampling. – Parks-Mc. Clellan. • We will just consider the window method.

Window Method • • First stage of this method is to calculate the coefficients of the ideal filter. This is calculated as follows: p 1 w ( ) = hd n H (w )e j n d w 2 p -p ò wc 1 w = 1 ×e j n d w 2 p -w ò c ì 2 fc sin (n wc ) ï =í n wc ïî 2 fc for n ¹ 0 for n = 0

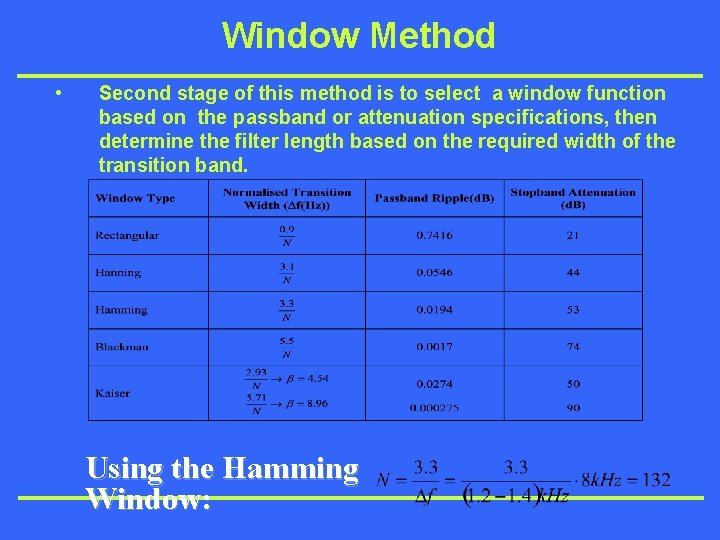
Window Method • Second stage of this method is to select a window function based on the passband or attenuation specifications, then determine the filter length based on the required width of the transition band. Using the Hamming Window:

Window Method • The third stage is to calculate the set of truncated or windowed impulse response coefficients, h[n]: for Where: for

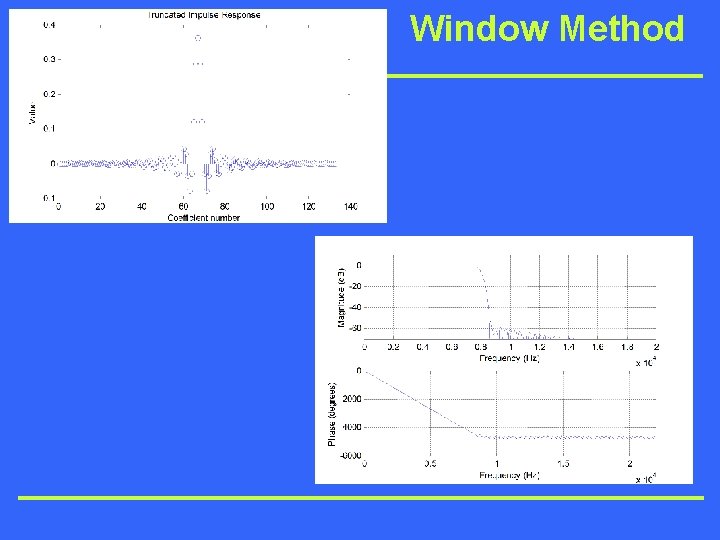
Window Method • Matlab code for calculating coefficients: close all; clear all; fc = 8000/44100; N = 133; n = -((N-1)/2): ((N-1)/2); n = n+(n==0)*eps; % cut-off frequency % number of taps [h] = sin(n*2*pi*fc). /(n*pi); [w] = 0. 54 + 0. 46*cos(2*pi*n/N); d = h. *w; % generate sequence of ideal coefficients % generate window function % window the ideal coefficients [g, f] = freqz(d, 1, 512, 44100); % transform into frequency domain for plotting figure(1) plot(f, 20*log 10(abs(g))); axis([0 2*10^4 -70 10]); % plot transfer function figure(2); stem(d); xlabel('Coefficient number'); ylabel ('Value'); title('Truncated Impulse Response'); figure(3) freqz(d, 1, 512, 44100); axis([0 2*10^4 -70 10]); % avoiding division by zero % plot coefficient values % use freqz to plot magnitude and phase response

Window Method

Equiripple Design • Starting point is minimax criterion, e. g. • Based on theory of Chebyshev approximation and the `alternation theorem’, which (roughly) states that the optimal ai’s are such that the `max’ (maximum weighted approximation error) is obtained at L+2 extremal frequencies… …that hence will exhibit the same maximum ripple (`equiripple’) • Iterative procedure for computing extremal frequencies, etc. (Remez exchange algorithm, Parks-Mc. Clellan algorithm) • Very flexible, etc. , available in many software packages • Details omitted here (see textbooks)

Software • FIR Filter design abundantly available in commercial software • Matlab: b=fir 1(n, Wn, type, window), windowed linear-phase FIR design, n is filter order, Wn defines band-edges, type is `high’, `stop’, … b=fir 2(n, f, m, window), windowed FIR design based on inverse fourier transform with frequency points f and corresponding magnitude response m b=remez(n, f, m), equiripple linear-phase FIR design with Parks-Mc. Clellan (Remez exchange) algorithm