Digital Signal Processing Digital Filters 1 Filter A

Digital Signal Processing Digital Filters 1

Filter: A filter is essentially a system or network that selectively changes the wave shape, amplitude-frequency and/or phasefrequency characteristics of a signal in a desired manner. n Common Filtering objectives are to improve the quality of a signal ( for example, to remove or reduce the noise), to extract the information from signal. n 2

Digital Filter: A digital filter is a mathematical algorithm implemented in hardware and/or software that operates on a digital input signal to produce a digital output signal for purpose of achieving a filtering task. A digital filter operates on a digitized analog signal or just numbers, representing some variables, stored in computer memory 3

Advantages of Digital Filters Digital filters have truly linear phase response that is not possible with analog filters. n The performance of the digital filters do not vary with environment changes, for example thermal variations. This eliminates the need of calibrate periodically. n The frequency response of a digital filter can be automatically adjusted, if it is implemented using a programmable processor. n 4

Advantages of Digital Filters (cont: ) Several input signals or channels can be filtered by one digital filter without the need to replicate the hardware. n Both filtered and unfiltered data can be saved for further use. n Advantage can be readily taken of the tremendous advancements in VLSI technology to fabricate the digital filters, and to make them small in size, to consume low power , and to keep the cost down. n Digital filters can be used at very low frequencies. Also Digital filter can be made to work over a wide range of frequencies by mere 5 change of sampling frequency. n

Disadvantages Speed Limitation n Finite word length effect n Long design and development times n 6

Filter Design Steps The design of a digital filter involves five steps: n Specifications of the filter requirements. n Calculation of suitable filter coefficients. n Representation of the filter by a suitable structure (realization). n Analysis of the effect of the finite word length on filter performance. n Implementation of filter in software and/ or hardware. 7

Digital Filters: A digital filter can be represented by the following equation: yn = b 0 xn + b 1 xn-1 + …. + b. Mxn-M + a 1 yn-1 + … + a. Pyn-P (1) This equation t Mathematically describes a digital filter t Can be directly implemented in a computer, real time processor, or special purpose hardware to do the actual filtering. 8

Types of digital filters Digital filters are broadly divided into two classes: n Finite Impulse Response (FIR) filters yn = b 0 xn + b 1 xn-1 + …. + b. Mxn-M I n Infinite Impulse response (IIR) filters yn = b 0 xn + b 1 xn-1 + …. + b. Mxn-M + a 1 yn-1 + … + a. Pyn-P 9

Choosing between FIR and IIR The choice between FIR and IIR filter depends largely on the relative advantages of the two filter types. FIR filters can have an exactly linear phase response. The implication of this is that no phase distortion is introduced into the signal by the filter. Where as the phase response of FIR filters are non linear, especially at the band edges. n FIR filters are realized non-recursively and are always stable. The stability of IIR filters can not always be guaranteed. n 10

Choosing between FIR and IIR (Cont: ) The effect of using a limited number of bits to implement filters such as round off noise, and coefficients quantization error are much less severe in FIR than IIR. n FIR requires more coefficients for the sharp cutoff filters than IIR. Thus for a given amplitude response specification, more processing time and storage will be required for FIR implementation. n Analog filters can be readily transformed into equivalent IIR digital filters meeting the similar specifications. This is not possible with the FIR filters, as they have no analog counter part. n 11

In general, n Use IIR when there are requirements such as sharp cutoff and high throughput. n Use FIR if the number of filter coefficients is not too large and in particular if little or no phase distortion is desired. 12

Finite Impulse Response (FIR) Filters Definition: These filters have all the a coefficients zero in equation (4): yn = b 0 xn + b 1 xn-1 + …… + b. Mxn-M Alternative Names: Non-recursive filters, Allzero filters. Reason for the name Finite Impulse Response filter: the unit impulse response consists of a finite number (M+1) of terms, i. e. its duration in real time is finite. (M+1) is called the filter Length. 13

Designing Frequency-Selective FIR Filters Ideally we wish to realize a “brick-wall” magnitude response and a linear phase response. In practice we can realize a reasonable approximation to this magnitude response, together with a linear phase response. The design problem may be stated thus: Given an ideal/desired frequency response Fd(jw), decide on a filter length and decide on a filter coefficients which will give an actual response F(jw) approximating to Fd(jw) to within a given specification in magnitude and phase. 14

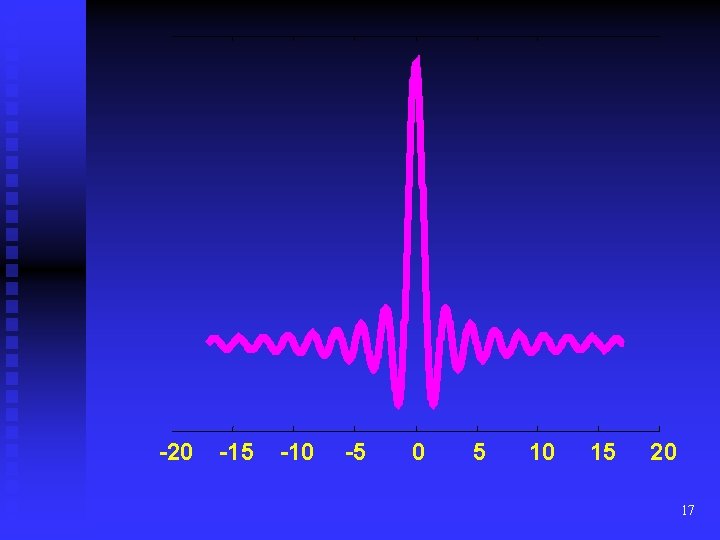
Design of FIR filter using Fourier Methods Transform Pair: (5) (6) To illustrate the method, we try to obtain a design for the ideal low-pass, zero delay filter Hd(w) = 1 00, -wc < wc (7) = 0, |w| > wc where wc is the cutoff frequency. On substituting this into (6) we get (8) 15

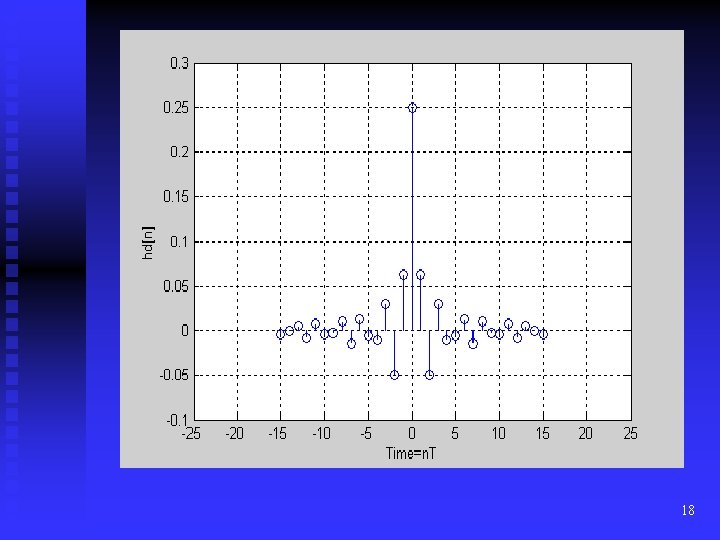
which evaluates to n = - …. (9) A filter with the impulse response (8) would realize the ideal specification (7) exactly, However, (a) This impulse response is infinite in length i. e. the (b) filter would require an infinite number o (c) coefficients. (d) Solution: Truncate to a finite number of coefficien (e) The response will now be an approximation to t (f) ideal. (g) (b) This impulse response is double-sided as (h) shown in the fig on the next slide. If we truncate th (i) series symmetrically, it will have terms for negat (j) k and the filter will be non-causal i. e. will requir (k) foreknowledge. It will not be realizable in real 16 tim

-20 -15 -10 -5 0 5 10 15 20 17

18

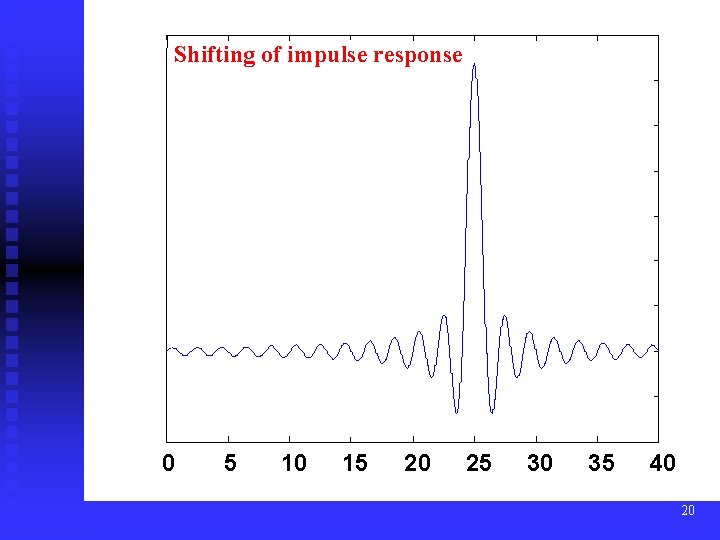
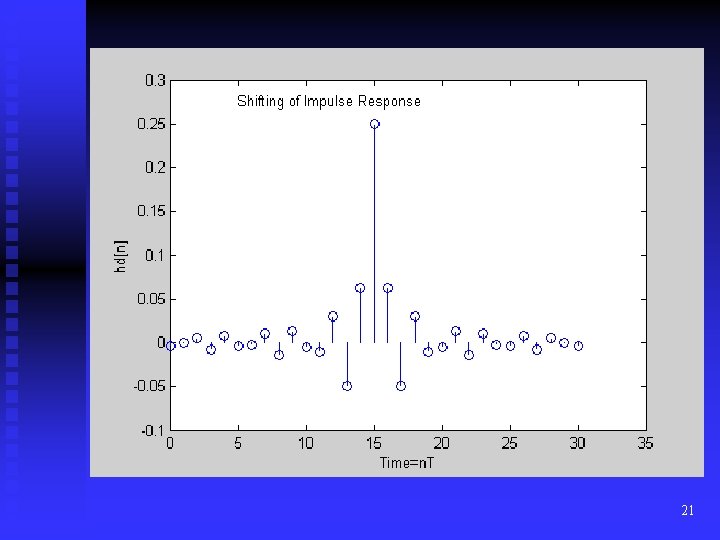
Solution: Shift the impulse response by N sampling intervals in time, where N = M/2. On denoting the shifted response by h[n], this gives h[n] = hd(n-N) (10) and now we have a standard finite length causal filter. This will have the effect of delaying the response by N sampling intervals. Instead of the zero delay filter of (7), we will have a constant delay filter with delay time . This is equivalent to a linear phase filter, the phase being given by = -2 f radians. On taking account of the truncation and the shift, (8) becomes (11) 19

Shifting of impulse response 0 5 10 15 20 25 30 35 40 20

21

The effect of truncation: The effect is to introduce Gibbs Oscillations into the frequency response. Reducing the effects of truncation: Increasing the filter length has relatively little effect. A better method is to window the impulse response: each term h[n] is multiplied by the corresponding term w[n] in a window: hw[n] = h[n]w[n] (12) Many windows have been proposed. Some of these are described below: 22

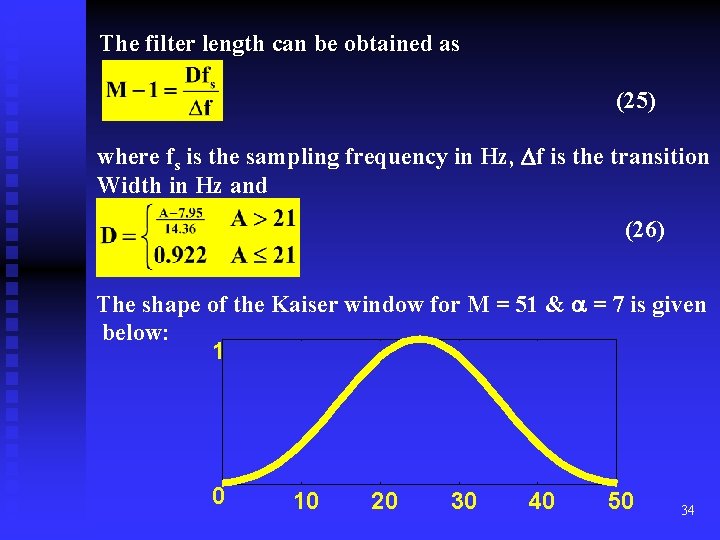
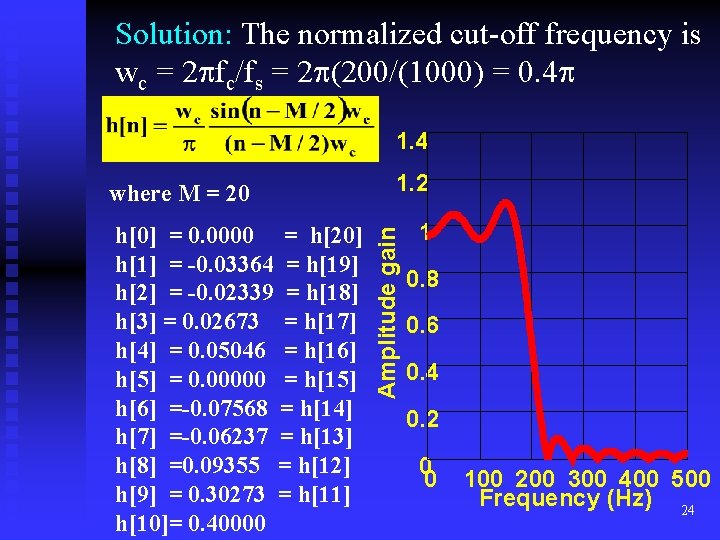
Rectangular Window: The rectangular window is defined as (13) The filter coefficients b[n] = h[n] can now be computed as (14) Example 1: Design a low-pass FIR filter with cut-off frequency at 200 Hz relative to a Nyquist frequency of 1 KHz. Use the rectangular window to truncate the impulse response. The length of the filter is 21. 23

Solution: The normalized cut-off frequency is wc = 2 fc/fs = 2 (200/(1000) = 0. 4 1. 4 h[0] = 0. 0000 = h[20] h[1] = -0. 03364 = h[19] h[2] = -0. 02339 = h[18] h[3] = 0. 02673 = h[17] h[4] = 0. 05046 = h[16] h[5] = 0. 00000 = h[15] h[6] =-0. 07568 = h[14] h[7] =-0. 06237 = h[13] h[8] =0. 09355 = h[12] h[9] = 0. 30273 = h[11] h[10]= 0. 40000 1. 2 Amplitude gain where M = 20 1 0. 8 0. 6 0. 4 0. 2 0 0 100 200 300 400 500 Frequency (Hz) 24

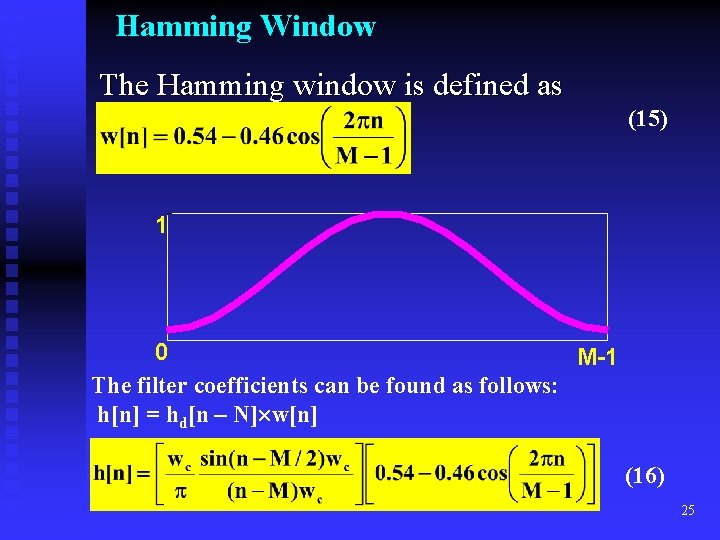
Hamming Window The Hamming window is defined as (15) 1 0 M-1 The filter coefficients can be found as follows: h[n] = hd[n – N] w[n] (16) 25

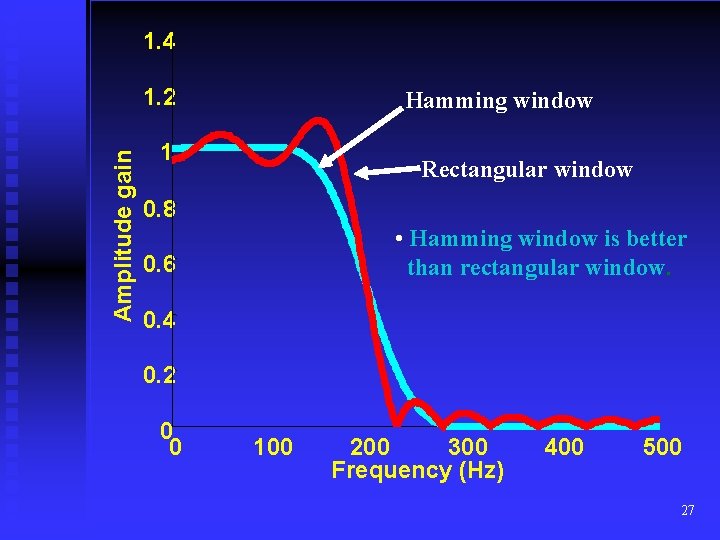
Example 2: Repeat example 1 for a Hamming window. The filter coefficients can be computed by using equation (16) as: h[0] = 0. 00000 = h[20] h[1] = -0. 00345 = h[19] h[2] = -0. 00393 = h[18] h[3] = 0. 00721 = h[17] h[4] = 0. 02007 = h[16] h[5] = 0. 00000 = h[15] h[6] = -0. 05163 = h[14] h[7] = -0. 05054 = h[13] h[8] = 0. 08533 = h[12] h[9] = 0. 29592 = h[11] h[10]= 0. 40000 The magnitude response of the filter and its comparison with the magnitude response of the filter with rectangular window is given in the figure on the next slide. 26

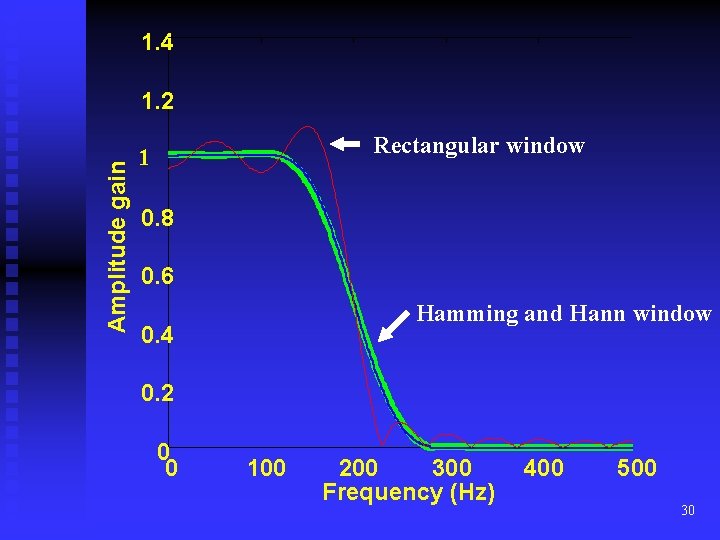
1. 4 Amplitude gain 1. 2 Hamming window 1 Rectangular window 0. 8 • Hamming window is better than rectangular window. 0. 6 0. 4 0. 2 0 0 100 200 300 Frequency (Hz) 400 500 27

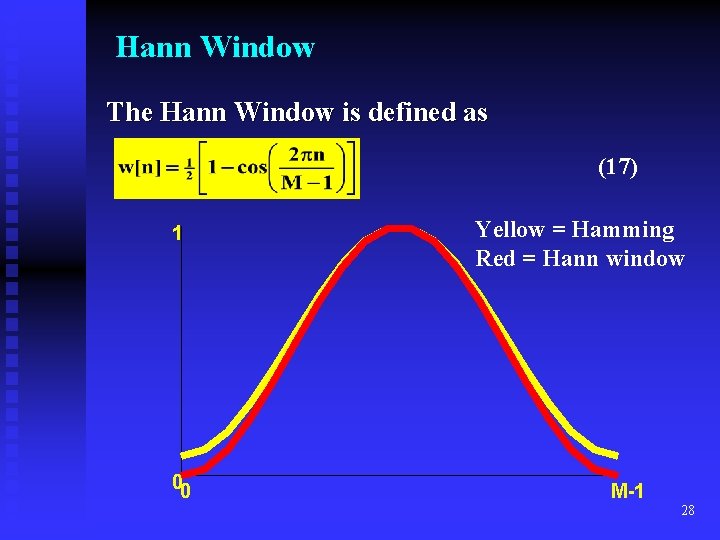
Hann Window The Hann Window is defined as (17) 1 00 Yellow = Hamming Red = Hann window M-1 28

Example 3: Repeat Example 1 with the Hann Window Solution: The coefficients of the filter in this case can be computed as follows: (18) The coefficients are: h[0] = 0. 00000 h[1] = -0. 00082 h[2] = -0. 00223 h[3] = 0. 00551 h[4] = 0. 01743 h[5] = 0. 0000 h[6] = -0. 04953 = h[20] = h[19] = h[18] = h[17] = h[16] = h[15] = h[14] h[7] = -0. 04951 = h[13] h[8] = 0. 08462 = h[12] h[9] = 0. 29532 = h[11] h[10] = 0. 40000 29

1. 4 Amplitude gain 1. 2 Rectangular window 1 0. 8 0. 6 Hamming and Hann window 0. 4 0. 2 0 0 100 200 300 Frequency (Hz) 400 500 30

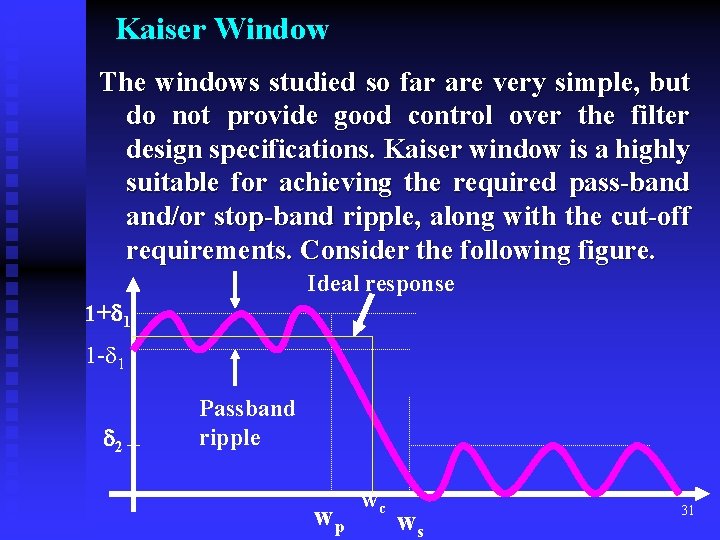
Kaiser Window The windows studied so far are very simple, but do not provide good control over the filter design specifications. Kaiser window is a highly suitable for achieving the required pass-band and/or stop-band ripple, along with the cut-off requirements. Consider the following figure. Ideal response 1+ 1 1 - 1 2 Passband ripple wp wc ws 31

The passband/stopband frequencies {wp, ws} are related to the ideal cutoff frequency wc and transition width w by wc = ½ (wp + ws), w = ws – wp (19) The passband stopband overshoots {Ap, As} are expressed in d. B as , (20) Equation (20) can be inverted to give: (21) Although 1 and 2 can be specified independently of each Other, it is a property of all windows designs that the final designed filter will have equal pass-band stop-band 32 ripples.

Therefore, we must design the filter on the basis of the smaller of the two ripples, that is, = min( 1, 2) (22) The Kaiser window is mathematically represented as (23) where I 0(x) is the modified Bessel function of the first kind And 0 th order. The parameter can be computed as follows: (24) 33

The filter length can be obtained as (25) where fs is the sampling frequency in Hz, f is the transition Width in Hz and (26) The shape of the Kaiser window for M = 51 & = 7 is given below: 1 0 10 20 30 40 50 34

Example 4: Using Kaiser Window, design a low-pass digital filter with the following specifications: Sampling frequency = 20 KHz pass-band frequency = 4 KHz Stop-band frequency = 5 KHz Ap = 0. 1 d. B, As = 80 d. B Solution: and Therefore, = min( 1, 2), which in db is A = -20 log 10 = As = 80. a= 0. 1102(A-8. 7) = 7. 857, D = (A-7. 95)/14. 36 = 5. 017. The transition width = fs – fp = 5 – 4 = 1 KHz fc = ½ (fs + fp) = 4. 5 KHz, wc = (2 fc/fs) = 0. 45. 35 M– 1 = Dfs/ f M = 103 (M-1)/2 = 102/2 = 51

The windowed impulse response will be (27) 36

Generalized FIR Digital Filter Design: The windows described above can easily be used to design a High-pass and other frequency selective filters FIR filter. Following are the main steps: n Define an ideal magnitude response function. n Obtain the ideal (infinite) impulse response sequence hd[n]by evaluating the Fourier inverse transform of the magnitude response of step 1. n Use appropriate delay factor and window to compute the coefficients of the filter. 37

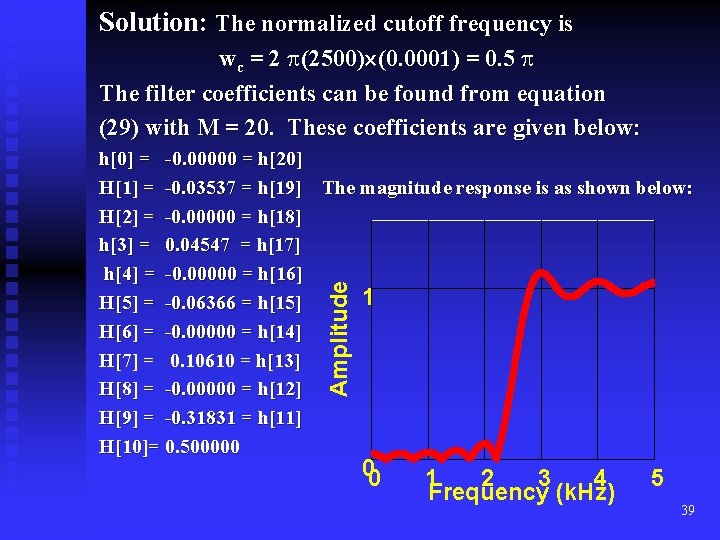
High Pass Filter: The magnitude response of a normalized ideal high-pass filter is given by (28) By evaluating the inverse Fourier Transform, we obtain the ideal impulse response sequence (29) Tutorial Q 1: Derive equation (29) from equation (28). Example 5: Design a high-pass filter with a cutoff frequency of 2. 5 KHz and a sample interval of 0. 0001 s; The length of the filter is 21 and the rectangular window is used to truncate the ideal impulse response function. 38

Solution: The normalized cutoff frequency is wc = 2 (2500) (0. 0001) = 0. 5 The filter coefficients can be found from equation (29) with M = 20. These coefficients are given below: Amplitude h[0] = -0. 00000 = h[20] H[1] = -0. 03537 = h[19] The magnitude response is as shown below: H[2] = -0. 00000 = h[18] h[3] = 0. 04547 = h[17] h[4] = -0. 00000 = h[16] 1 H[5] = -0. 06366 = h[15] H[6] = -0. 00000 = h[14] H[7] = 0. 10610 = h[13] H[8] = -0. 00000 = h[12] H[9] = -0. 31831 = h[11] H[10]= 0. 500000 00 1 2 3 4 Frequency (k. Hz) 5 39

Band-Pass Filter: The magnitude of an ideal constant delay band-pass filter is given by (30) where w. L and w. H are the low and high edges of the pass-band M/2 is the delay. When Hd(w) of (30) is inverse transformed, we find that the Band-pass impulse response is given by (31) Tutorial Q 2: Derive equation (31) from (30) 40

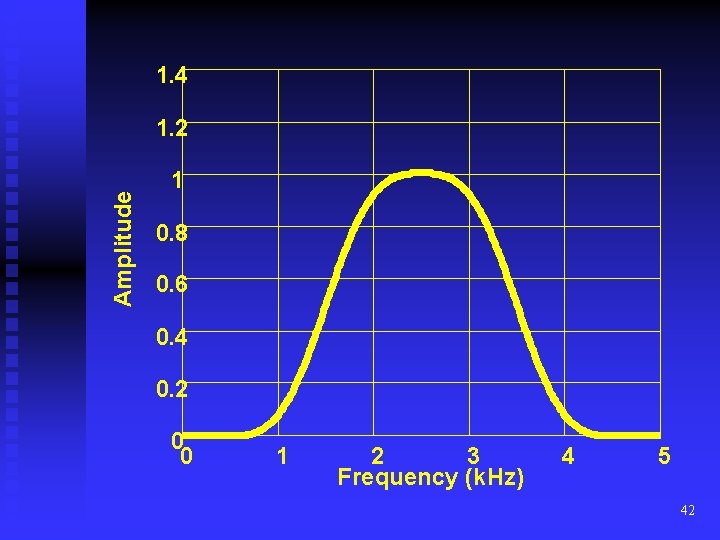
Example 6: Design a Band-Pass Digital FIR filter of length 21. The band edges are specified to be at 1. 5 and 3. 5 k. Hz and the sampling interval is 0. 0001 s. Use the Hamming window. Solution: The normalized cutoff frequencies are. 15 and 0. 35. The filter coefficients are obtained by multiplying (31) and (15) and are given below: h[0] = 0. 00000 = h[20] h[8] = -0. 27614 = h[12] h[1] = -0. 00000 = h[19] h[9] = 0. 000000 = h[11] h[2] = -0. 01270 = h[18] h[10] = 0. 40000 h[3] = 0. 00000 = h[17] The magnitude response of the h[4] = 0. 02481 = h[16] Designed filter is shown h[5] = 0. 00000 =h[15] overleaf h[6] = 0. 06381 =h[14] H[7] = -0. 00000 = h[13] 41

1. 4 Amplitude 1. 2 1 0. 8 0. 6 0. 4 0. 2 0 0 1 2 3 Frequency (k. Hz) 4 5 42

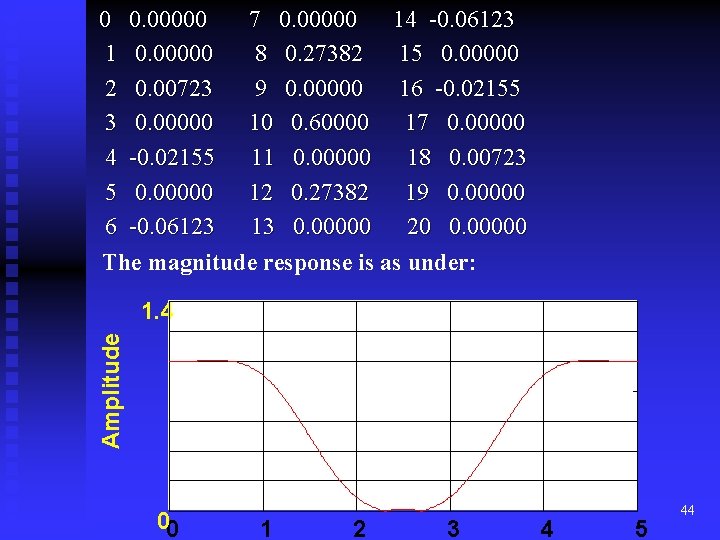
Band-Stop Filter: The ideal frequency response of a Band-Stop filter is given by (32) where w. L and w. H now specify the low and high edges of the stop-band. Taking the inverse Fourier transform of (32) yileds (33) Example 7: Design a band-stop filter with edges frequencies At 1. 5 and 3. 5 k. Hz relative to a sample interval of 0. 0001. Use Hanning window. Length of the filter is 21. Solution: the normalized frequencies are 0. 15 and. 35. The Filter coefficients can be obtained by multiplying (33) and (17 43 and are given by

0 0. 00000 7 0. 00000 14 -0. 06123 1 0. 00000 8 0. 27382 15 0. 00000 2 0. 00723 9 0. 00000 16 -0. 02155 3 0. 00000 10 0. 60000 17 0. 00000 4 -0. 02155 11 0. 00000 18 0. 00723 5 0. 00000 12 0. 27382 19 0. 00000 6 -0. 06123 13 0. 00000 20 0. 00000 The magnitude response is as under: Amplitude 1. 4 00 1 2 3 4 5 44