Digital Logic Design Truth Table Logic Circuit 1

Digital Logic Design

Truth Table Logic Circuit 1. 2. Start with truth table When your output is a 1, figure out the combination of inputs, ANDs, and NOTs Example: 3. When you have all your “miniterms, ” OR all of them together Example: 4. 5. A = 0, B = 1, C = 0 A’·B·C’ A = 1, B = 1, C = 0 A·B·C’ f = A’·B·C’ + A·B·C’ Simplify your boolean expression Build your digital circuit

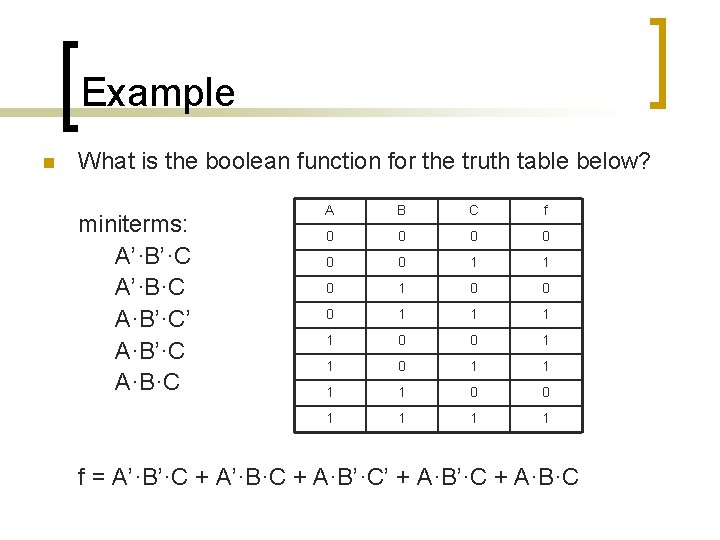
Example n What is the boolean function for the truth table below? miniterms: A’·B’·C A’·B·C A·B’·C’ A·B’·C A·B·C A B C f 0 0 0 1 1 1 1 0 0 1 1 1 1 f = A’·B’·C + A’·B·C + A·B’·C’ + A·B’·C + A·B·C

Example n Simplify the boolean expression f = A’·B’·C + A’·B·C + A·B’·C’ + A·B’·C + A·B·C f = A’·C + A·B’ + A·B·C f = A’·C + A ( B’ + C ) n Build the digital circuit from the simplified expression

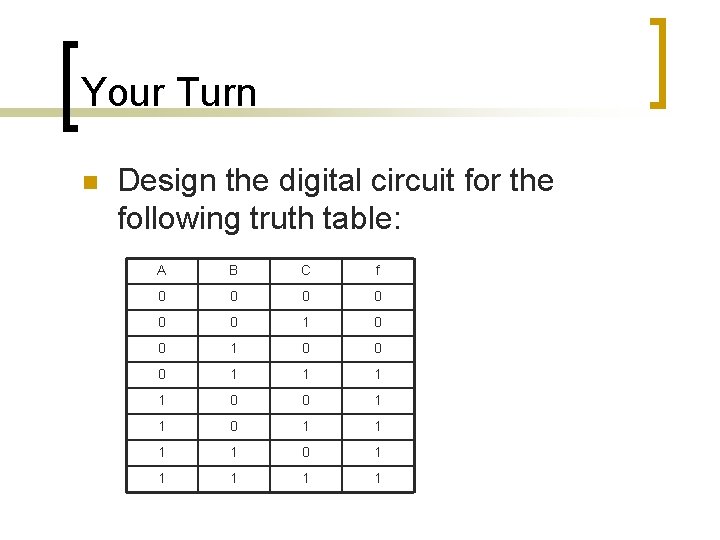
Your Turn n Design the digital circuit for the following truth table: A B C f 0 0 0 1 1 0 0 1 1 1 1 0 1 1 1

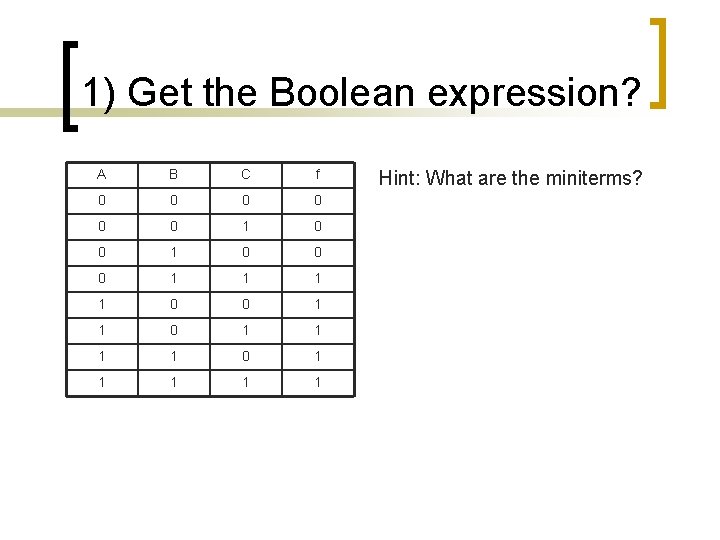
1) Get the Boolean expression? A B C f 0 0 0 1 1 0 0 1 1 1 1 0 1 1 1 Hint: What are the miniterms?

2) Simplify! f = A’·B·C + A·B’·C’ + A·B’·C + A·B·C’ + A·B·C

3) Build the Digital Circuit f = A + B·C

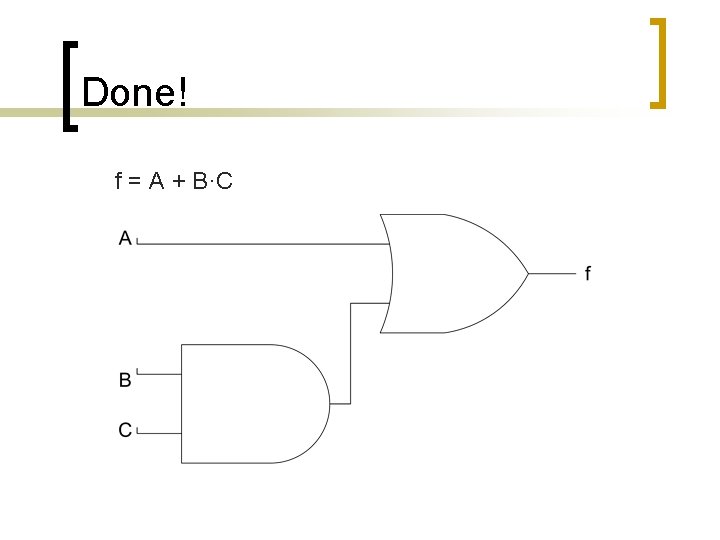
Done! f = A + B·C