Digital Logic Design n Basics Adapted from the

Digital Logic Design n Basics Adapted from the slides prepared by S. Dandamudi for the book, Fundamentals of Computer Organization and Design.

Introduction to Digital Logic Basics n Hardware consists of a few simple building blocks Ø n These are called logic gates n AND, OR, NOT, … n NAND, NOR, XOR, … Logic gates are built using transistors n n n NOT gate can be implemented by a single transistor AND gate requires 3 transistors Transistors are the fundamental devices n n n Pentium consists of 3 million transistors Compaq Alpha consists of 9 million transistors Now we can build chips with more than 100 million transistors

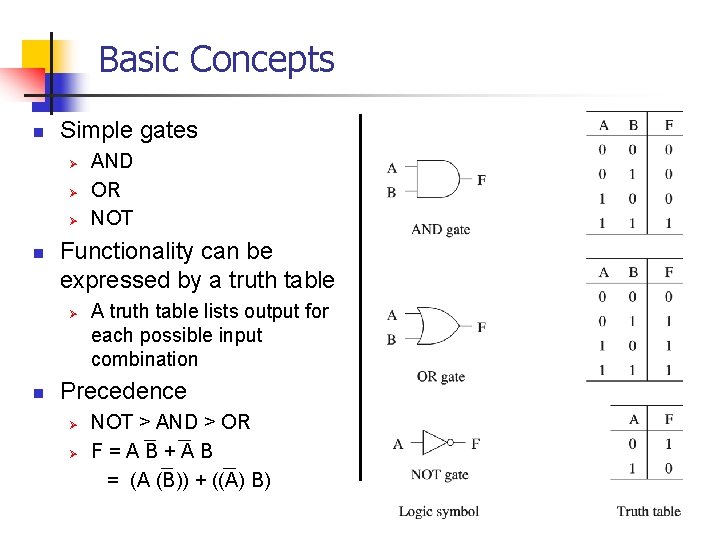
Basic Concepts n Simple gates Ø Ø Ø n Functionality can be expressed by a truth table Ø n AND OR NOT A truth table lists output for each possible input combination Precedence Ø Ø NOT > AND > OR F=AB+AB = (A (B)) + ((A) B)

Basic Concepts (cont. ) n Additional useful gates Ø Ø Ø n n NAND NOR XOR NAND = AND + NOT NOR = OR + NOT XOR implements exclusive -OR function NAND and NOR gates require only 2 transistors Ø AND and OR need 3 transistors!

Basic Concepts (cont. ) n Number of functions Ø Ø With N logical variables, we can define N 2 2 functions Some of them are useful n AND, NOR, XOR, … Some are not useful: n Output is always 1 n Output is always 0 “Number of functions” definition is useful in proving completeness property

Basic Concepts (cont. ) n Complete sets Ø A set of gates is complete n If we can implement any logical function using only the type of gates in the set n Ø Ø You can uses as many gates as you want Some example complete sets n {AND, OR, NOT} Not a minimal complete set n {AND, NOT} n {OR, NOT} n {NAND} n {NOR} Minimal complete set n A complete set with no redundant elements.

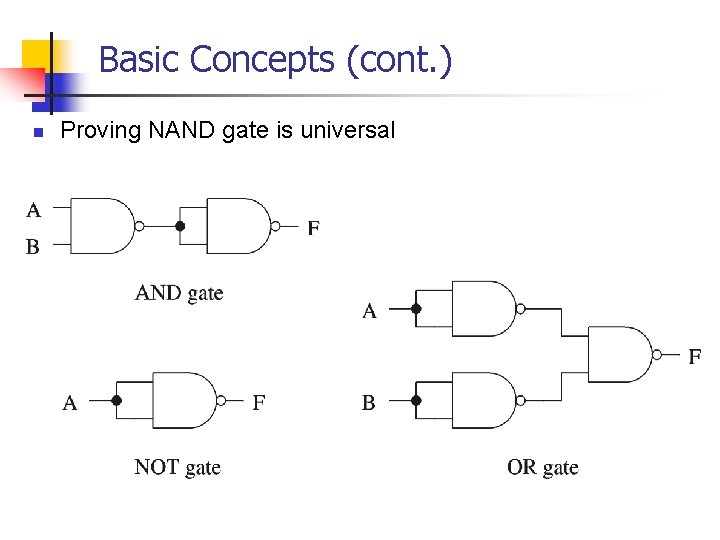
Basic Concepts (cont. ) n Proving NAND gate is universal

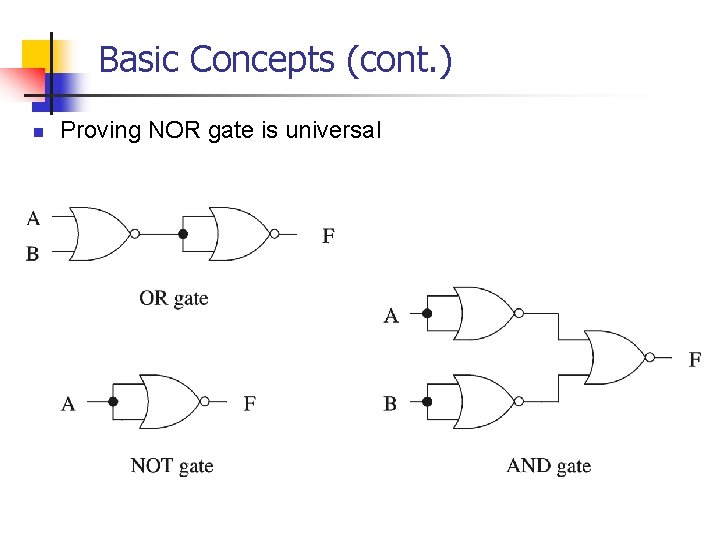
Basic Concepts (cont. ) n Proving NOR gate is universal

Logic Chips (cont. )

Logic Chips (cont. ) n Integration levels Ø Ø SSI (small scale integration) n Introduced in late 1960 s n 1 -10 gates (previous examples) MSI (medium scale integration) n Introduced in late 1960 s n 10 -100 gates LSI (large scale integration) n Introduced in early 1970 s n 100 -10, 000 gates VLSI (very large scale integration) n Introduced in late 1970 s n More than 10, 000 gates

Logic Functions n Logical functions can be expressed in several ways: Ø Ø Ø n Truth table Logical expressions Graphical form Example: Ø Majority function n Output is one whenever majority of inputs is 1 n We use 3 -input majority function

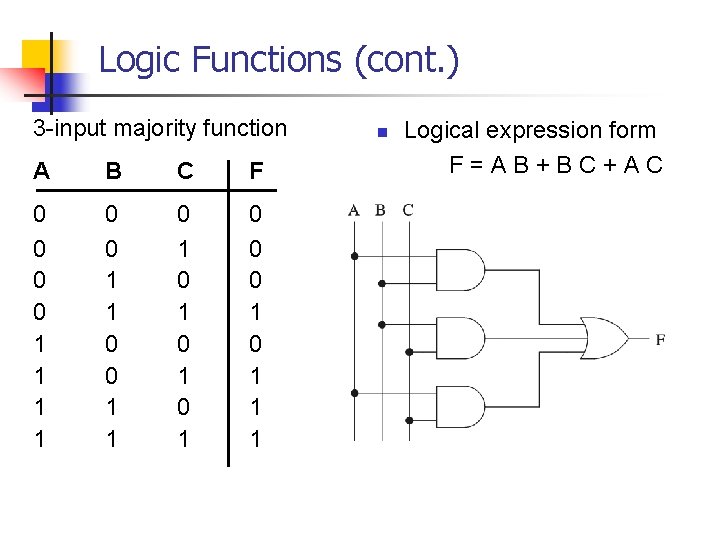
Logic Functions (cont. ) 3 -input majority function A B C F 0 0 1 1 0 1 0 1 0 0 0 1 1 1 n Logical expression form F=AB+BC+AC

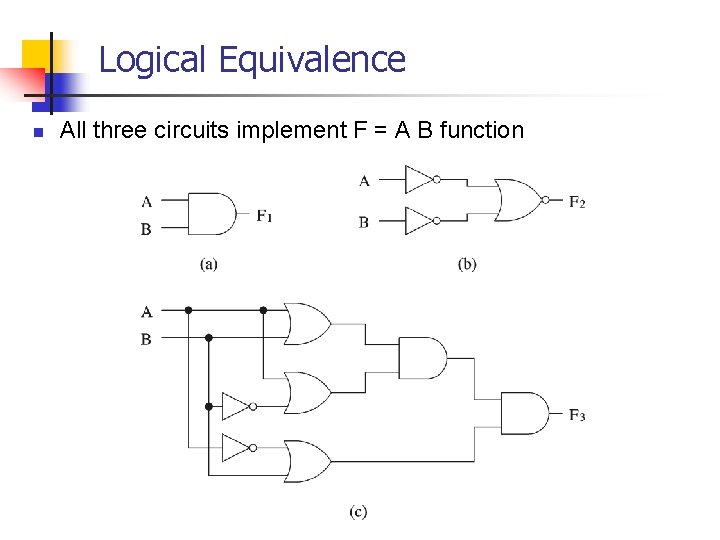
Logical Equivalence n All three circuits implement F = A B function