Digital Logic Design Digital Systems and Binary Numbers

Digital Logic Design

Digital Systems and Binary Numbers ( 1 st –Chapter ) Numbers with Different Bases Binary (base 2) Octal (base 8) Hexadecimal (base 16) 8 1000 10 8 1 9 1001 11 9 2 2 10 1010 12 A 11 3 3 11 1011 13 B 4 100 4 4 12 1100 14 C 5 101 5 5 13 1101 15 D 6 110 6 6 14 1110 16 E 7 0111 7 7 15 1111 17 F Decimal (base 10) Binary (base 2) Octal (base 8) Hexadecimal (base 16) 0 0 1 1 1 2 10 3 Decimal (base 10)

Multiplication, Addition, Subtraction. Multiplication Questions‐: 1. (11)2 * (01)2 2. (111)2 * (101)2 3. (101. 1)2 * (111. 1)2 Subtraction Using Fraction‐: 1. (66. 7520)10 – (9. 2658)10 2. (1111. 0000)2 – (. 1010)2 Addition Using Fraction‐: 1. (100. 12)10 + (67. 27)10 2. (010101. 11)2 + (111111. 10)2

Multiplication, Addition, Subtraction. Complements Of Numbers-: Complements are used in digital computers to simplify the subtraction operation and for logical manipulation. Simplifying operations leads to simpler, less expensive circuits to implement the operations. There are two types of complements for each base‐r system: the radix complement and the diminished radix complement. The first is referred to as the r’s complement and the second as the (r ‐ 1)>s complement. When the value of the base r is substituted in the name, the two types are referred to as the 2’s complement and 1’s complement for binary numbers and the 10’s complement and 9’s complement for decimal numbers. N = is Numbers, n = is Total digits, r = is Base

Subtraction with complements The subtraction of two n‐ digits unsigned numbers M – N in base r can be done as follows:

Complements 10 s or 2 s Complement‐: Subtraction with 10 s‐Complement‐: 1. N = (7634) )10 1. M = (72532)10 2. N = (11011)10 N = (3250)10 9 s or 1 s Complement‐: Subtraction with 2 s‐Complement: 1. N = (7543)10 1. M = (1010100)2 2. N = (101)2 3. N = (0. 0110)2 N = (1000011)2

Complements Subtraction Using 2 s‐Complement‐: 1. M = (110010)2 N = (110100)2 Subtraction Using 1 s‐Complement: 1. M = (110101)2 N = (100101)2 Subtraction Using 1 s‐Complement‐: 1. M = (101011)2 N = (111001)2 Subtraction Using 9 s‐Complement‐: 1. M = (215)10 N = (155)10

LOGICAL GATES Logical gate is a digital circuit that is able to operate on a number of binary inputs in order to perform logical function, A logical gate have one or more than one inputs but only one output. Basic Gates 1) AND Gate. 2) OR Gate. 3) NOT Gate.

LOGICAL GATES AND Gate ‐: Ø AND gate have two or more than two inputs and only one output. Ø The output of AND gate becomes ON if and only if all inputs are 1. AND Gate Truth Table Y=A. B A B Y = A. B 0 0 0 1 0 1 1 1

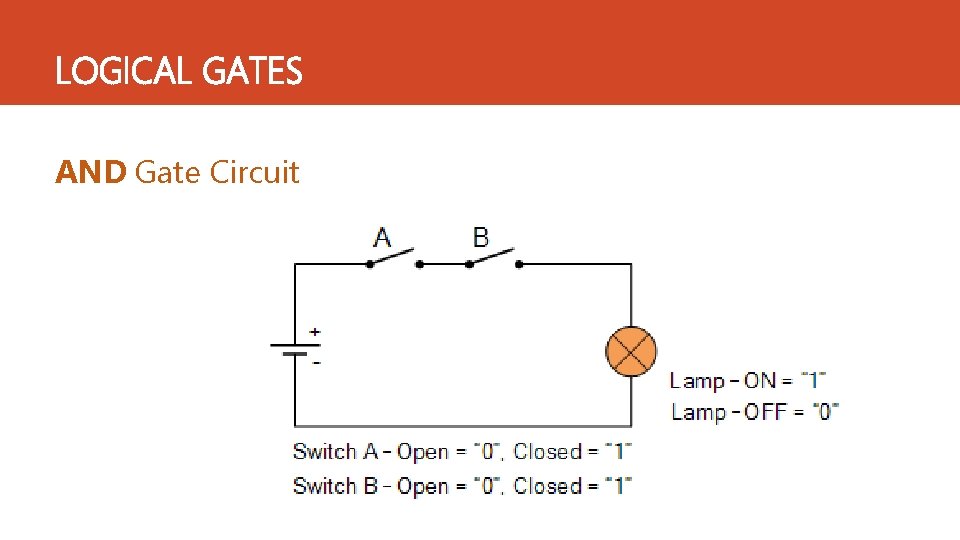
LOGICAL GATES AND Gate Circuit

LOGICAL GATES OR Gate ‐: Ø Two or more than two inputs but only one output. Ø Output of OR gate will be 1 if at least one operand has the value one, and otherwise gives a value of zero. OR Gate Truth Table Y=A+B A B Y = A+B 0 0 0 1 0 1 1 1

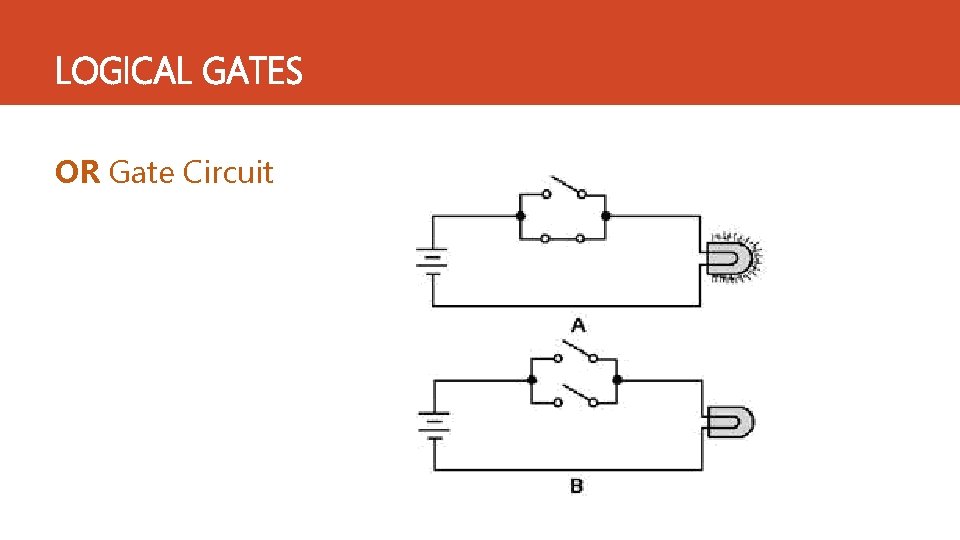
LOGICAL GATES OR Gate Circuit

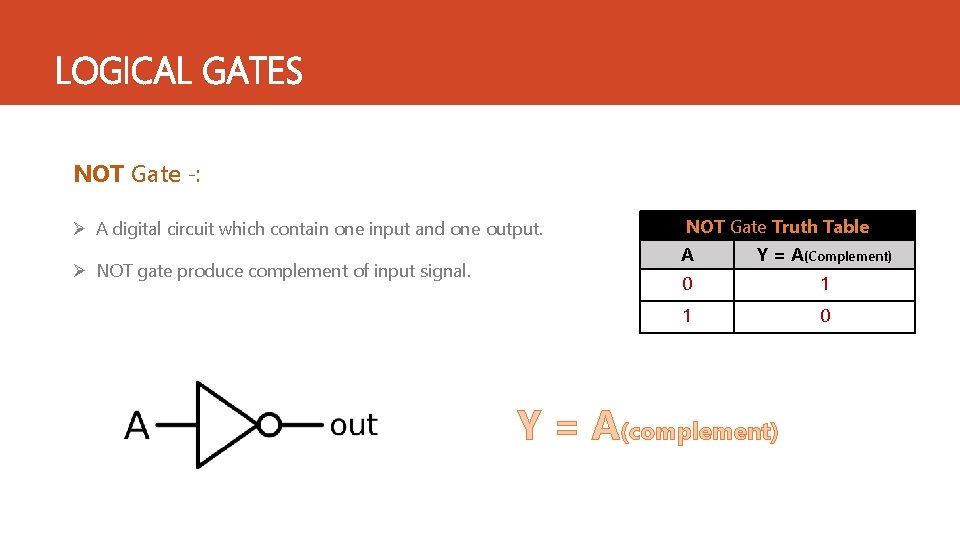
LOGICAL GATES NOT Gate ‐: Ø A digital circuit which contain one input and one output. Ø NOT gate produce complement of input signal. NOT Gate Truth Table A Y = A(Complement) 0 1 1 0 Y = A(complement)

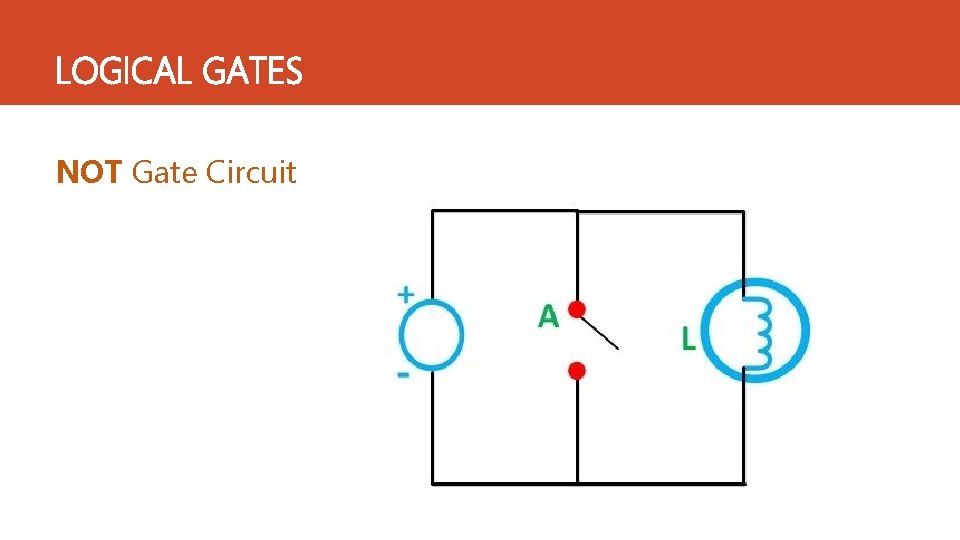
LOGICAL GATES NOT Gate Circuit

End Thank You All (have a nice day)