Digital Logic Design Combinational Logic Circuits Continue Functions

Digital Logic Design Combinational Logic Circuits Continue (Functions of CC) 1

Combinational Circuit Implementation of Decoders Binary Adder 2

Implementing a Binary Adder Using a Decoder S(X, Y, Z) = m (1, 2, 4, 7) C(X, Y, Z) = m (3, 5, 6, 7) 3 inputs and 8 minterms Use a 3 -to-8 decoder. 3

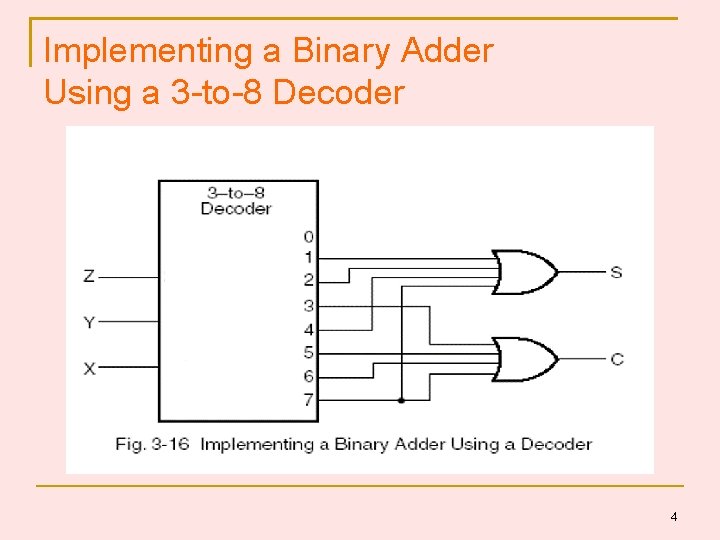
Implementing a Binary Adder Using a 3 -to-8 Decoder 4

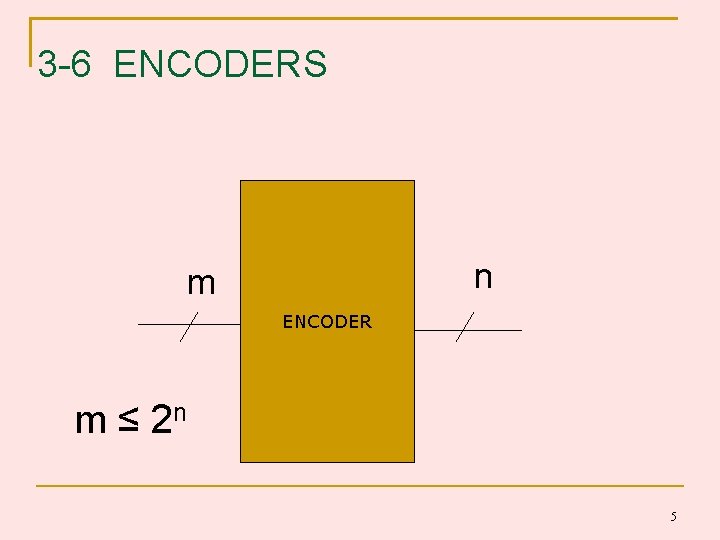
3 -6 ENCODERS n m ENCODER m ≤ 2 n 5

3 -6 ENCODERS Inverse operation of decoder. The output lines generate the binary code corresponding to the input value. Assume only 1 input has the value of 1 at any given time. Example: Octal-to-binary encoder. 6

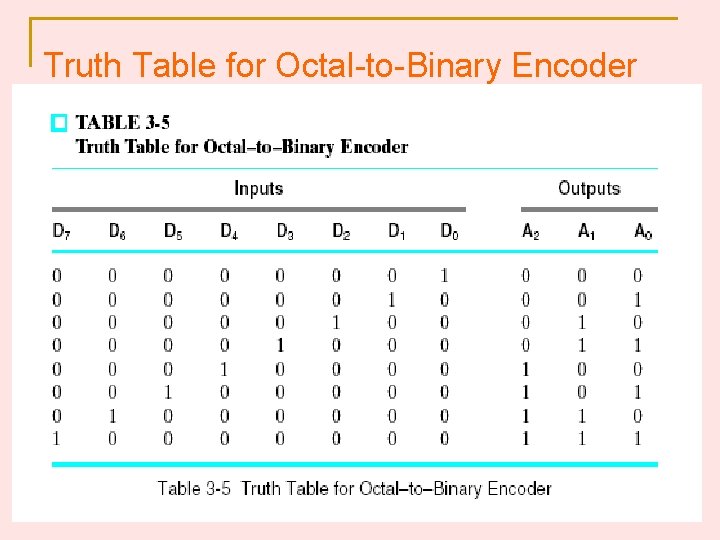
Truth Table for Octal-to-Binary Encoder 7

Priority Encoder 8

What about when 2 inputs are 1 at the same time? Use “Priority Encoder” To ensure only one input is encoded. e. g. D 3 = D 6 = 1 Output = 110 (D 6 has a higher priority than D 3) 9

Priority Encoder … If 2 or more inputs are equal to 1 at the same time, the input having the highest priority is the one encoded. Example: 4 -input Priority Encoder V (valid) =1 when 1 or more input is equal to 1. 10

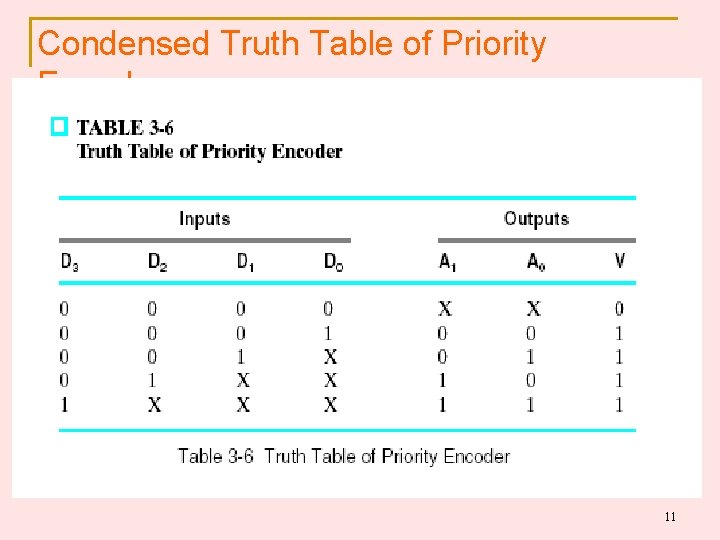
Condensed Truth Table of Priority Encoder X @ output => don’t care X @ input => product term that is not minterm 11

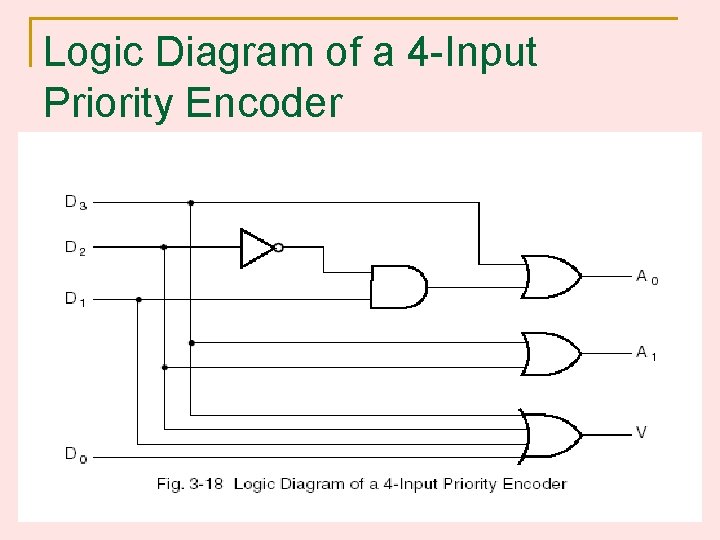
Logic Diagram of a 4 -Input Priority Encoder 12

Functions of Combinational Logic Adder Comparator Multiplexer Parity Generator Code Converters Encoder Demultiplexer Parity Checker 13

ADDERS Half Adder Full Adder 14

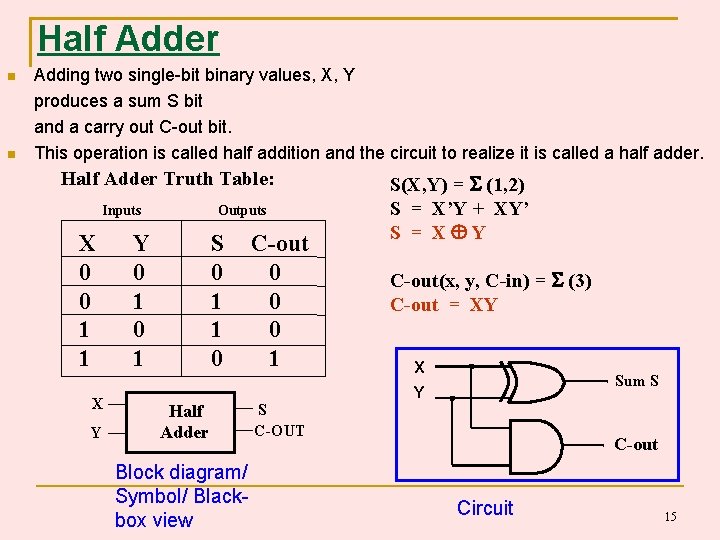
Half Adder Adding two single-bit binary values, X, Y produces a sum S bit and a carry out C-out bit. This operation is called half addition and the circuit to realize it is called a half adder. Half Adder Truth Table: Outputs Inputs X 0 0 1 1 X Y Y 0 1 S 0 1 1 0 Half Adder Block diagram/ Symbol/ Blackbox view C-out 0 0 0 1 S C-OUT S(X, Y) = (1, 2) S = X’Y + XY’ S = X Y C-out(x, y, C-in) = (3) C-out = XY X Sum S Y C-out Circuit 15

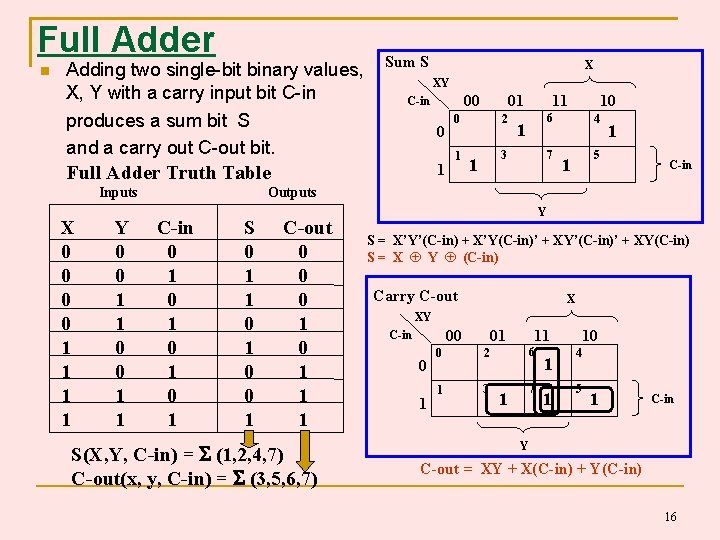
Full Adder Adding two single-bit binary values, X, Y with a carry input bit C-in produces a sum bit S and a carry out C-out bit. Sum S XY 0 1 01 0 1 2 11 6 1 3 1 10 7 4 1 5 1 C-in Outputs Inputs Y 0 0 1 1 00 C-in Full Adder Truth Table X 0 0 1 1 X C-in 0 1 0 1 S 0 1 1 0 0 1 C-out 0 0 0 1 1 1 S(X, Y, C-in) = (1, 2, 4, 7) C-out(x, y, C-in) = (3, 5, 6, 7) Y S = X’Y’(C-in) + X’Y(C-in)’ + XY’(C-in)’ + XY(C-in) S = X Y (C-in) Carry C-out X XY 00 C-in 0 1 01 0 2 1 3 11 6 7 1 10 4 5 1 C-in Y C-out = XY + X(C-in) + Y(C-in) 16

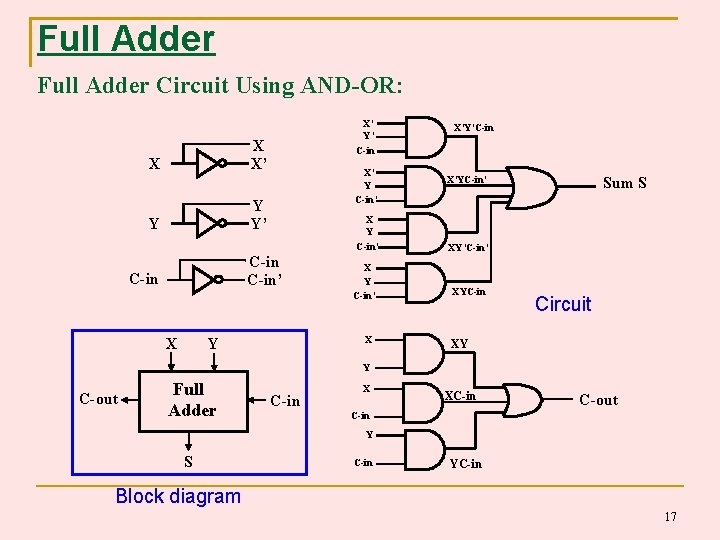
Full Adder Circuit Using AND-OR: X’ Y’ C-in X X’ Y C-in’ Y Y’ Y C-in’ X Sum S X’YC-in’ X Y C-in’ C-in X’Y’C-in X Y C-in’ X Y XY’C-in’ XYC-in Circuit XY Y C-out Full Adder C-in X XC-in C-out C-in Y S C-in YC-in Block diagram 17

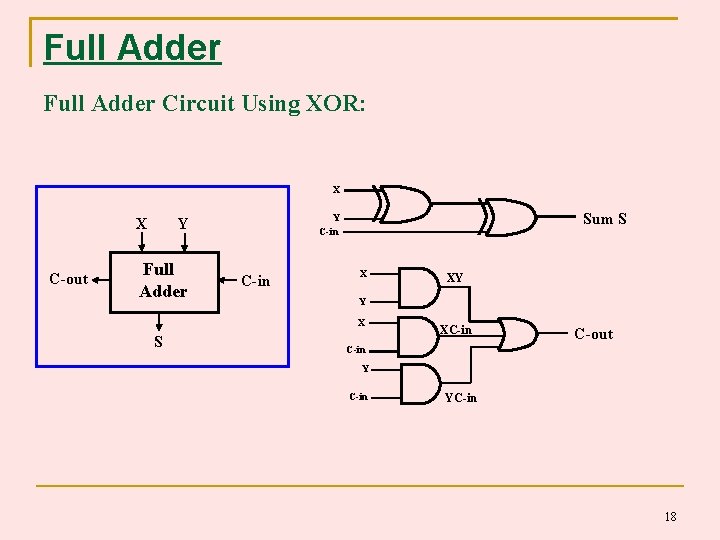
Full Adder Circuit Using XOR: X X C-out Full Adder Sum S Y C-in X Y X S XY XC-in C-out C-in YC-in 18

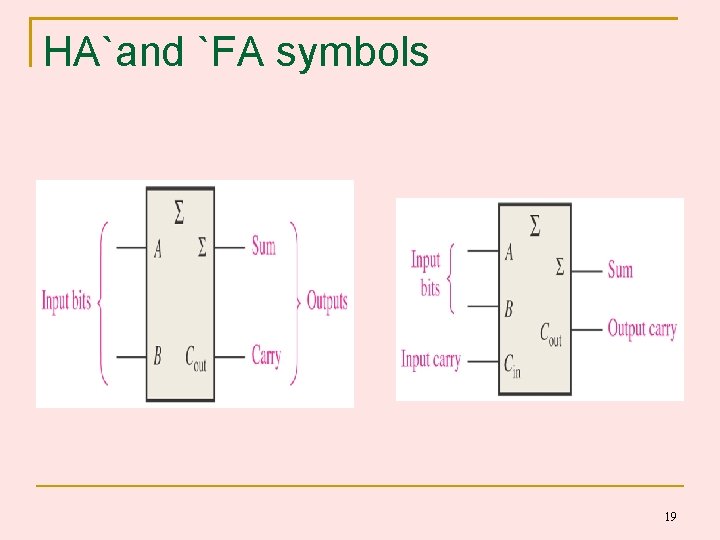
HA`and `FA symbols 19

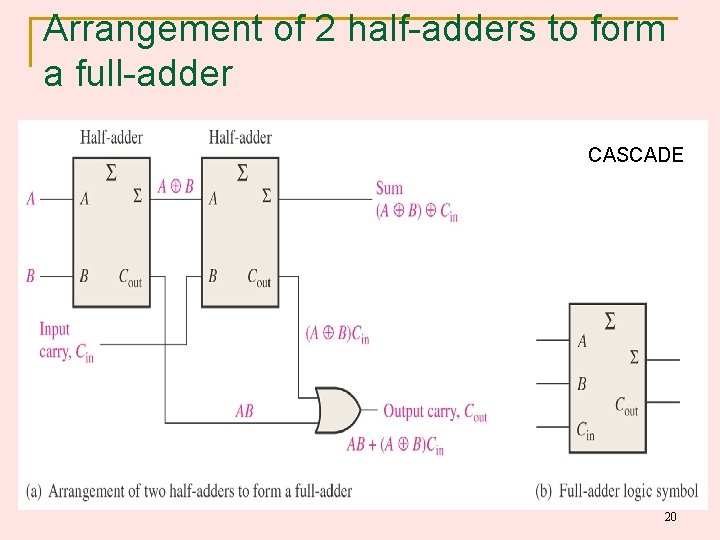
Arrangement of 2 half-adders to form a full-adder CASCADE 20

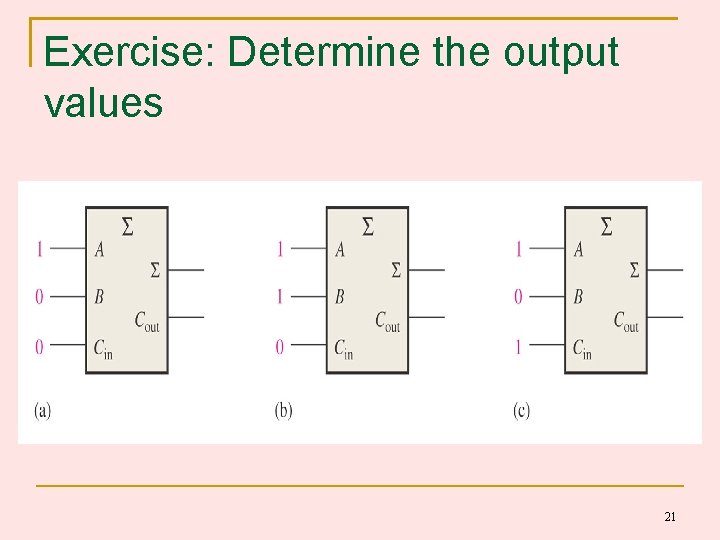
Exercise: Determine the output values 21

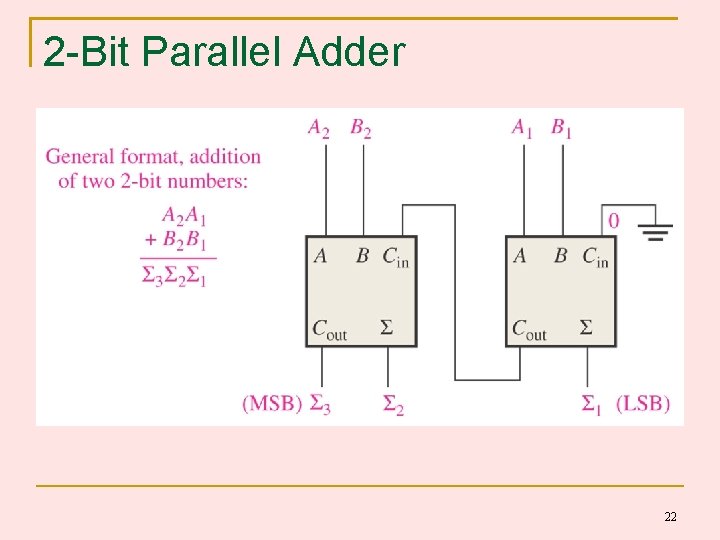
2 -Bit Parallel Adder 22

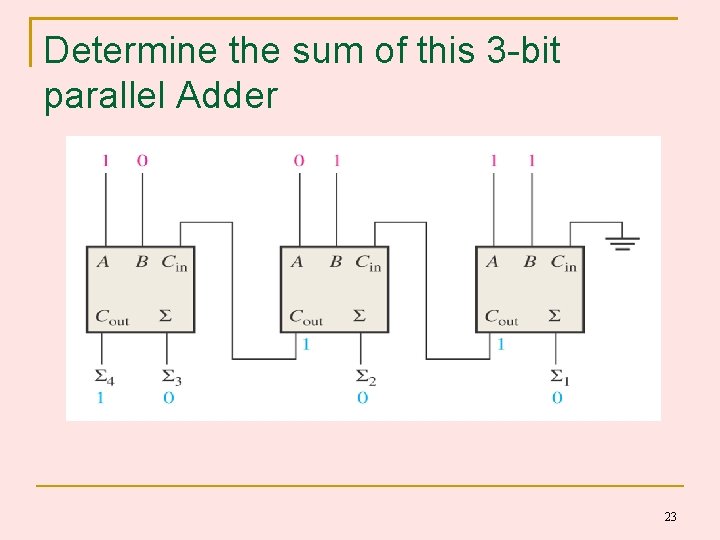
Determine the sum of this 3 -bit parallel Adder 23

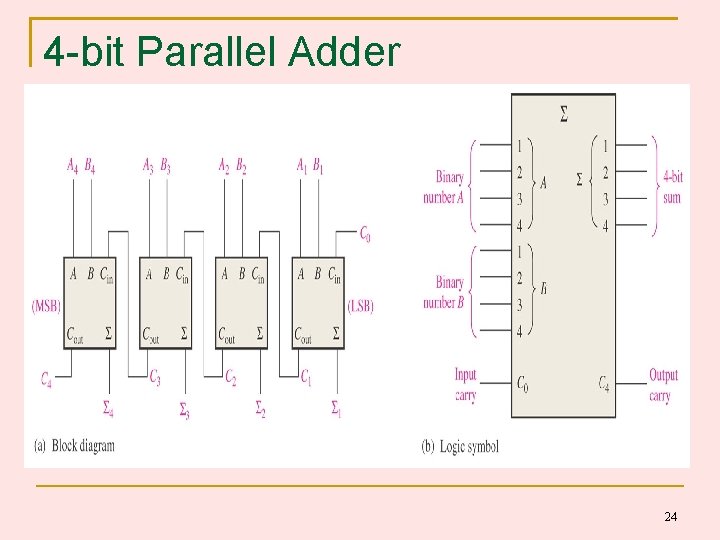
4 -bit Parallel Adder 24

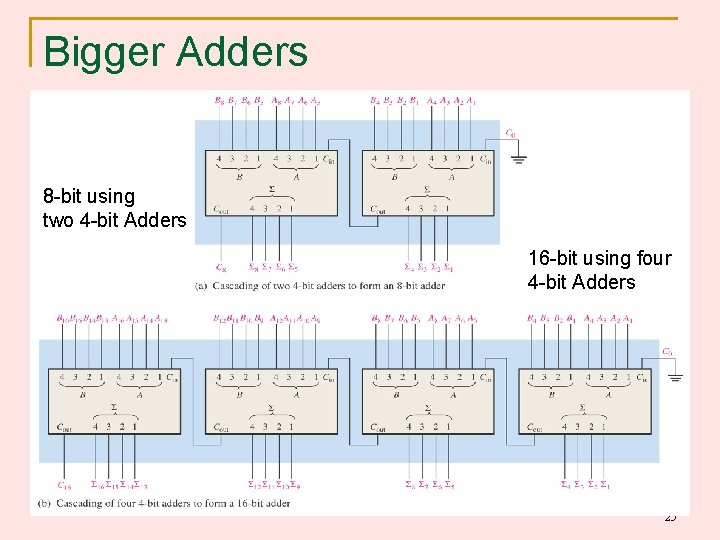
Bigger Adders 8 -bit using two 4 -bit Adders 16 -bit using four 4 -bit Adders 25

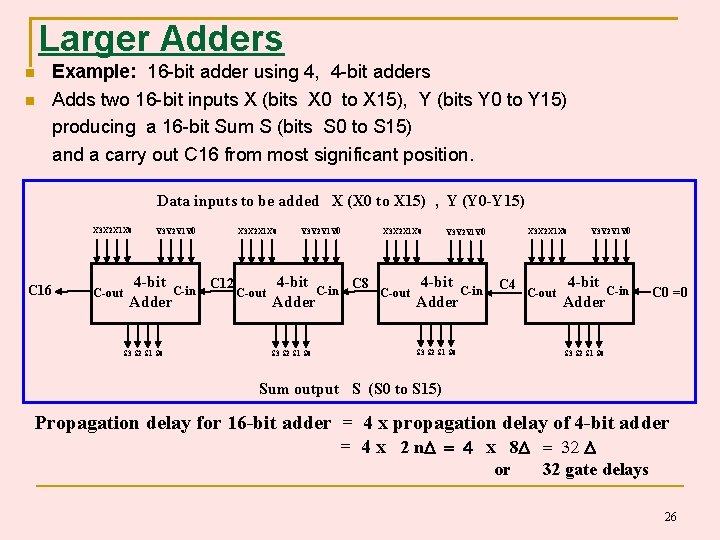
Larger Adders Example: 16 -bit adder using 4, 4 -bit adders Adds two 16 -bit inputs X (bits X 0 to X 15), Y (bits Y 0 to Y 15) producing a 16 -bit Sum S (bits S 0 to S 15) and a carry out C 16 from most significant position. Data inputs to be added X (X 0 to X 15) , Y (Y 0 -Y 15) X 3 X 2 X 1 X 0 C 16 C-out Y 3 Y 2 Y 1 Y 0 X 3 X 2 X 1 X 0 Y 3 Y 2 Y 1 Y 0 4 -bit C 12 C 8 C-in C-out Adder S 3 S 2 S 1 S 0 X 3 X 2 X 1 X 0 C-out Y 3 Y 2 Y 1 Y 0 4 -bit C-in Adder X 3 X 2 X 1 X 0 C 4 S 3 S 2 S 1 S 0 C-out Y 3 Y 2 Y 1 Y 0 4 -bit C-in Adder C 0 =0 S 3 S 2 S 1 S 0 Sum output S (S 0 to S 15) Propagation delay for 16 -bit adder = 4 x propagation delay of 4 -bit adder = 4 x 2 n x 8 or 32 gate delays 26

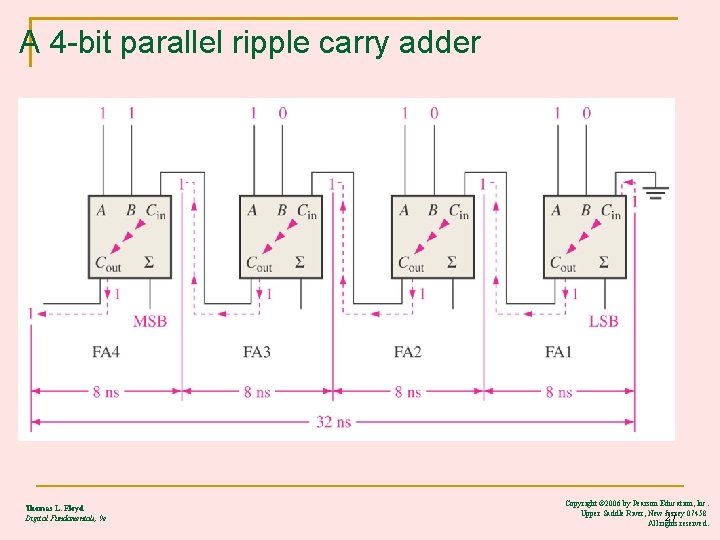
A 4 -bit parallel ripple carry adder Thomas L. Floyd Digital Fundamentals, 9 e Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 27 All rights reserved.

n-bit Carry Ripple Adders An n-bit adder used to add two n-bit binary numbers can built by connecting in series n full adders. Each full adder represents a bit position j (from 0 to n-1). Each carry out C-out from a full adder at position j is connected to the carry in C-in of the full adder at the higher position j+1. The output of a full adder at position j is given by: Sj = X j Y j C j Cj+1 = Xj. Yj + Xj. Cj + Y. Cj In the expression of the sum Cj must be generated by the full adder at the lower position j-1. The propagation delay in each full adder to produce the carry is equal to two gate delays = 2 Since the generation of the sum requires the propagation of the carry from the lowest position to the highest position , the total propagation delay of the adder is approximately: Total Propagation delay = 2 n 28

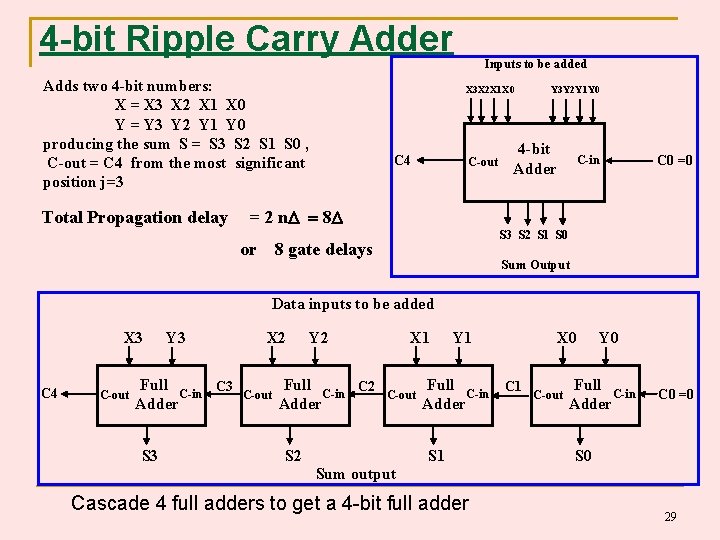
4 -bit Ripple Carry Adder Adds two 4 -bit numbers: X = X 3 X 2 X 1 X 0 Y = Y 3 Y 2 Y 1 Y 0 producing the sum S = S 3 S 2 S 1 S 0 , C-out = C 4 from the most significant position j=3 Total Propagation delay Inputs to be added X 3 X 2 X 1 X 0 C 4 C-out Y 3 Y 2 Y 1 Y 0 4 -bit Adder C 0 =0 C-in = 2 n 8 or S 3 S 2 S 1 S 0 8 gate delays Sum Output Data inputs to be added X 3 C 4 C-out Y 3 Full C 3 C-in Adder S 3 X 2 C-out Y 2 Full C 2 C-in Adder X 1 C-out S 2 Y 1 Full C-in Adder S 1 X 0 C 1 C-out Y 0 Full C-in Adder C 0 =0 S 0 Sum output Cascade 4 full adders to get a 4 -bit full adder 29

1’s Complement and 2’s Complement Hardware The 2’s complement of a binary number is formed by adding 1 to the 1’s complement. 2’s complement = (1’s complement) + 1 30

How to use an adder as a Subtractor? 31

Building a Subtractor using an Adder and 2’s Complement (for positive numbers) A – B = A + (-B) = A + B + 1 2’s complement To perform subtraction using an adder, we invert B, and use Cin =1. Try drawing this diagram… 32

Comparator Equality Comparator Inequality Comparator 33

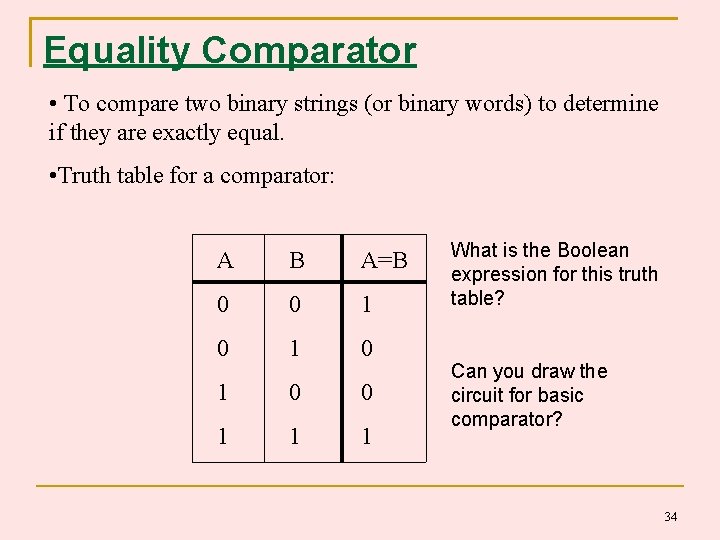
Equality Comparator • To compare two binary strings (or binary words) to determine if they are exactly equal. • Truth table for a comparator: A B A=B 0 0 1 0 1 0 0 1 1 1 What is the Boolean expression for this truth table? Can you draw the circuit for basic comparator? 34

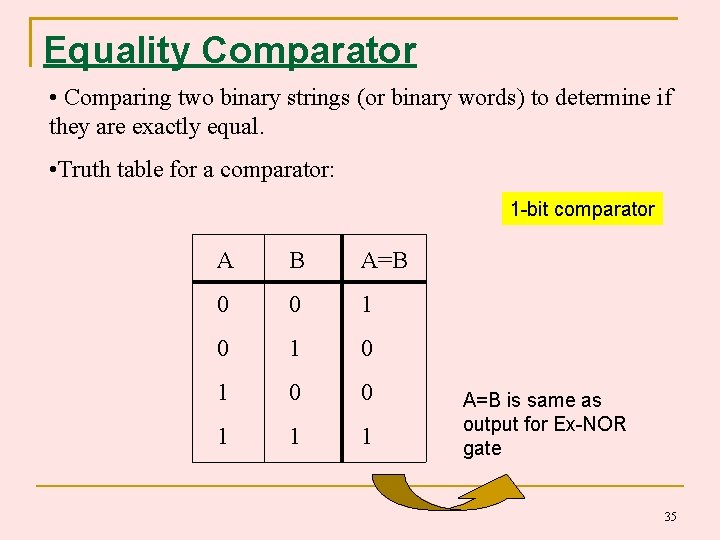
Equality Comparator • Comparing two binary strings (or binary words) to determine if they are exactly equal. • Truth table for a comparator: 1 -bit comparator A B A=B 0 0 1 0 1 0 0 1 1 1 A=B is same as output for Ex-NOR gate 35

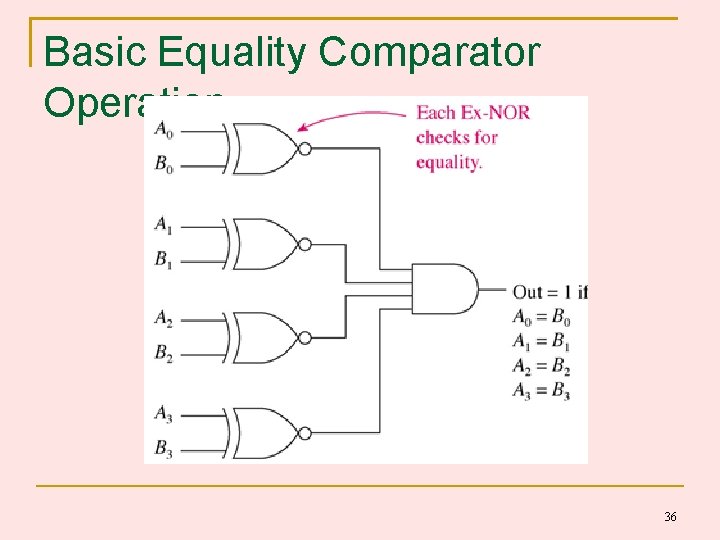
Basic Equality Comparator Operation 36

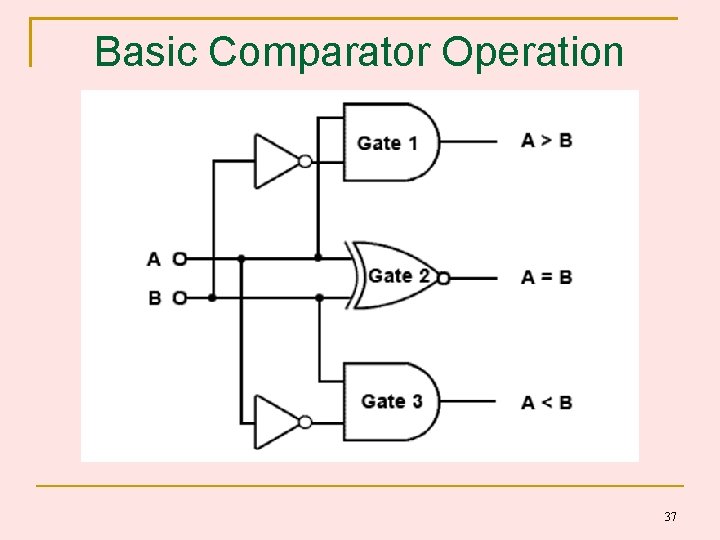
Basic Comparator Operation 37

1 -bit Comparator with Inequality outputs To compare 2 binary numbers, each 1 -bit wide. The result of the comparison are single bit outputs that indicate whether the numbers are equal to each other, or if one number is greater than or less than another. A=B? A<B? A>B? 38

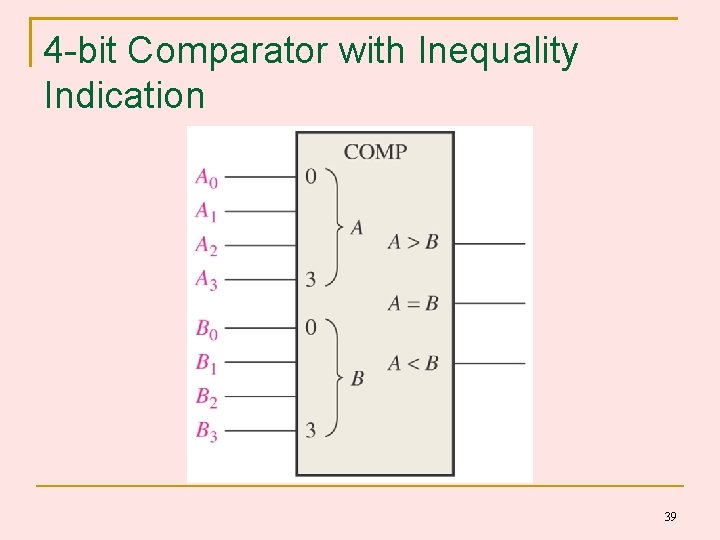
4 -bit Comparator with Inequality Indication 39

Multiplexers & Demultiplexers MUX & DEMUX 40

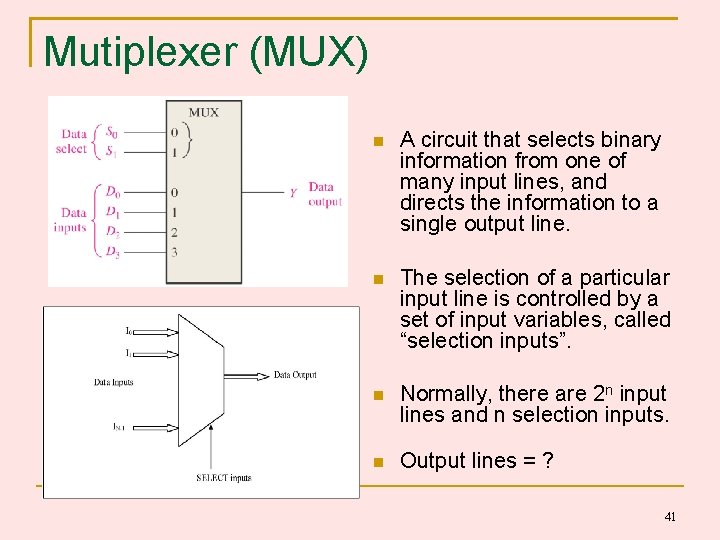
Mutiplexer (MUX) A circuit that selects binary information from one of many input lines, and directs the information to a single output line. The selection of a particular input line is controlled by a set of input variables, called “selection inputs”. Normally, there are 2 n input lines and n selection inputs. Output lines = ? 41

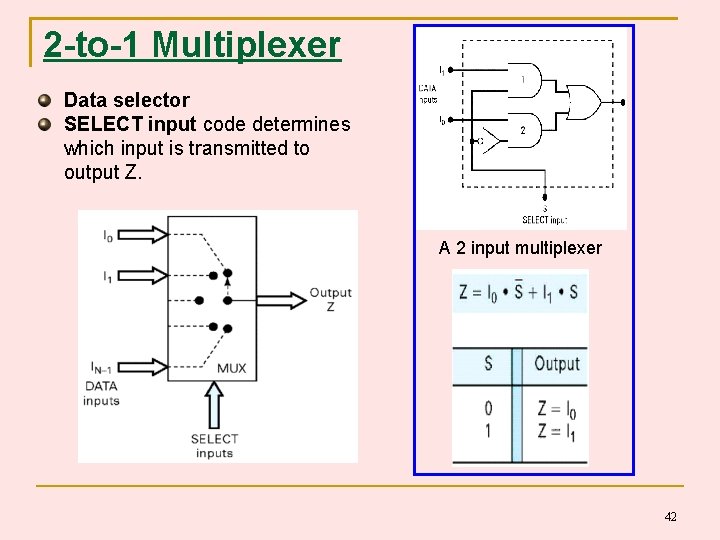
2 -to-1 Multiplexer Data selector SELECT input code determines which input is transmitted to output Z. A 2 input multiplexer 42

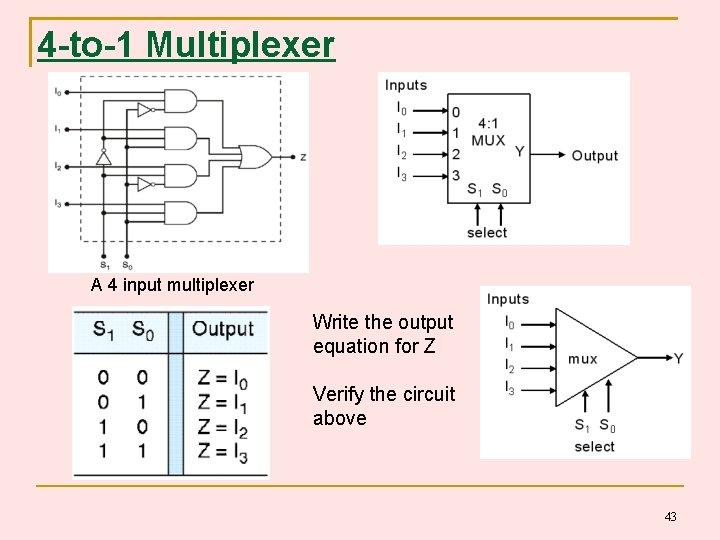
4 -to-1 Multiplexer A 4 input multiplexer Write the output equation for Z Verify the circuit above 43

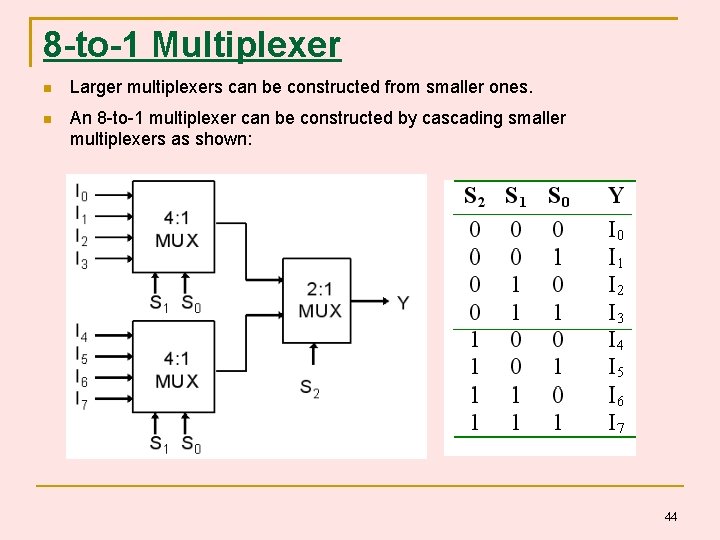
8 -to-1 Multiplexer Larger multiplexers can be constructed from smaller ones. An 8 -to-1 multiplexer can be constructed by cascading smaller multiplexers as shown: 44

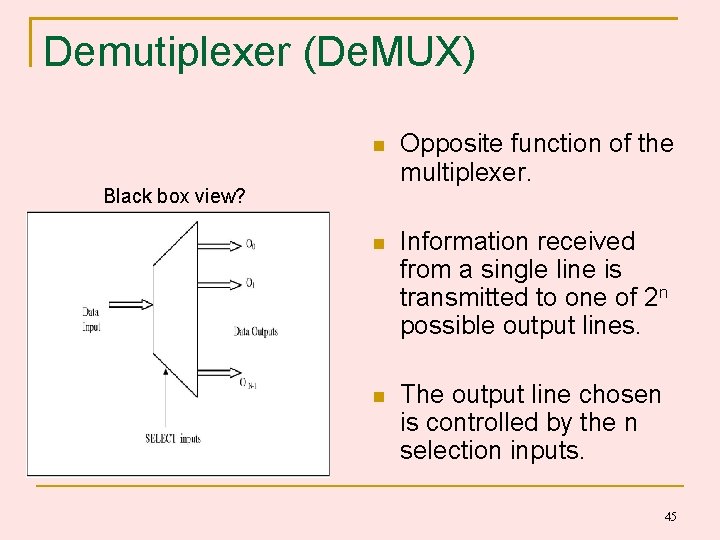
Demutiplexer (De. MUX) Opposite function of the multiplexer. Information received from a single line is transmitted to one of 2 n possible output lines. The output line chosen is controlled by the n selection inputs. Black box view? 45

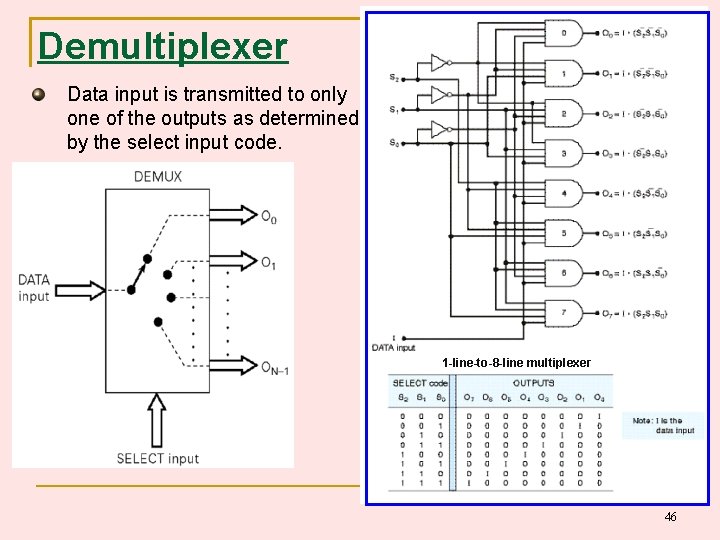
Demultiplexer Data input is transmitted to only one of the outputs as determined by the select input code. 1 -line-to-8 -line multiplexer 46

1 -to-2 De. MUX Select Y 0 Black box view Output equations Y 1 0 0 D 1 D 0 Logic circuit 47

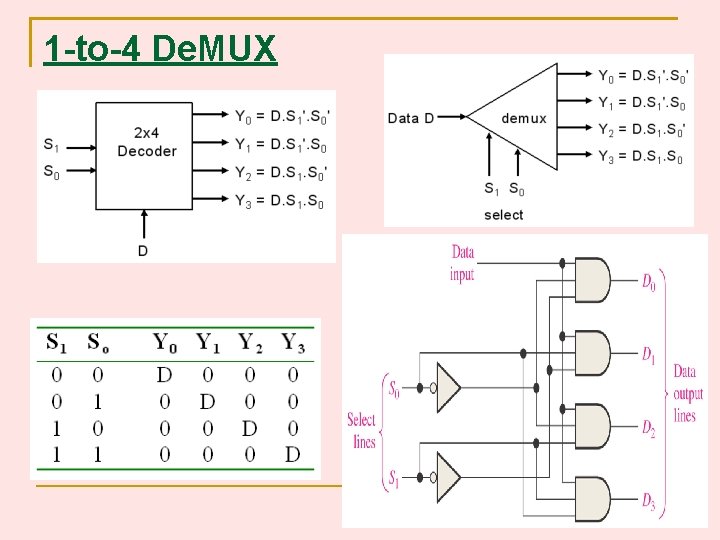
1 -to-4 De. MUX 48

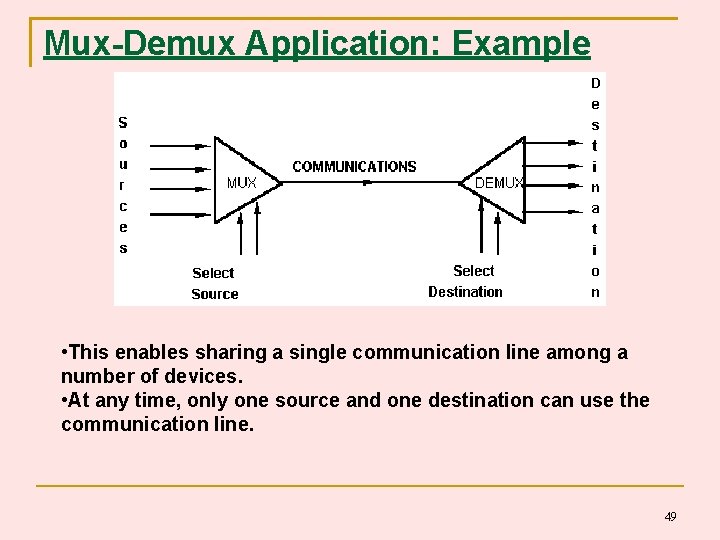
Mux-Demux Application: Example • This enables sharing a single communication line among a number of devices. • At any time, only one source and one destination can use the communication line. 49

Parity Generator & Parity Checker Odd Parity Even Parity 50

Error-Detection A parity bit is a scheme for detecting errors during transmission of binary info. A parity bit is an extra bit included with the binary message to make the number of 1’s either odd or even. The message, including the parity bit, is transmitted and then checked at the receiving end for errors. An error is detected if the checked parity does not correspond to the one transmitted. 51

Error-Detection The circuit that generates the parity bit in the transmitter is a parity generator. The circuit that checks the parity bit in the receiver is a parity checker. 52

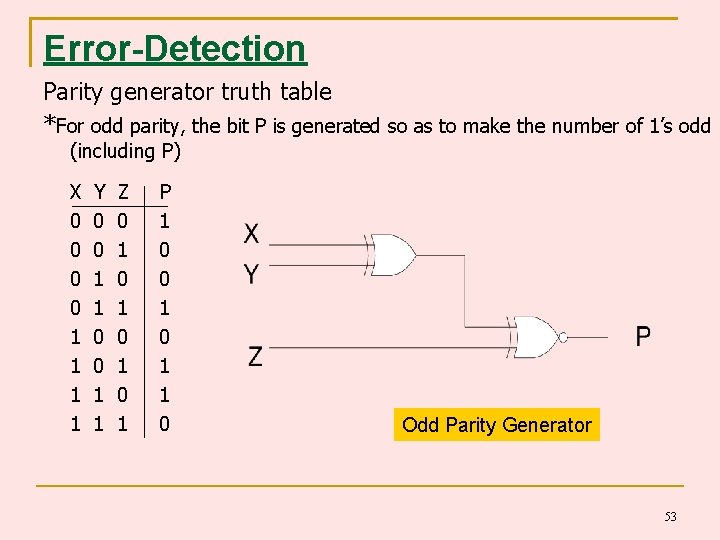
Error-Detection Parity generator truth table *For odd parity, the bit P is generated so as to make the number of 1’s odd (including P) X 0 0 1 1 Y 0 0 1 1 Z 0 1 0 1 P 1 0 0 1 1 0 Odd Parity Generator 53

*The three-bit message (X, Y, Z) and parity bit (P) are transmitted to their destination, where they are applied to a parity checker circuit. An error occurs during transmission if the parity of the four bits is even, since the binary info transmitted was originally odd. The output C of the parity checker should be a 1 when an error occurs, i. e. when the number of 1’s in the four inputs is even. X Y Z P C 0 0 1 0 0 1 1 1 0 0 0 0 1 1 0 1 0 1 1 1 0 0 0 0 1 1 1 0 1 1 0 0 1 Odd Parity Checker 1 1 0 1 1 1 0 0 1 1 1 54

• Parity is used in digital circuits to check for errors in transmission. • In Four bit transmission a parity bit is added to make the fifth bit. • In a eight bit transmission a parity bit is added to made a ninth bit. • And so on. 55

ODD Parity • In ODD parity when we add the bits together disregarding weight we get or want to get an odd number. 0000 is a four bit message add a parity bit to make it odd 10000 Odd parity is satisfied Parity bit 00011000 is an eight bit message add a parity bit to make it odd 000011001 Odd parity is satisfied 56

EVEN parity • In EVEN parity when we add the bits together disregarding weight we get or want to get an even number. 0001 is a four bit message add a parity bit to make it even Parity bit 00000 Even parity is satisfied 00011001 is an eight bit message add a parity bit to make it even 000111001 Even parity is satisfied 57

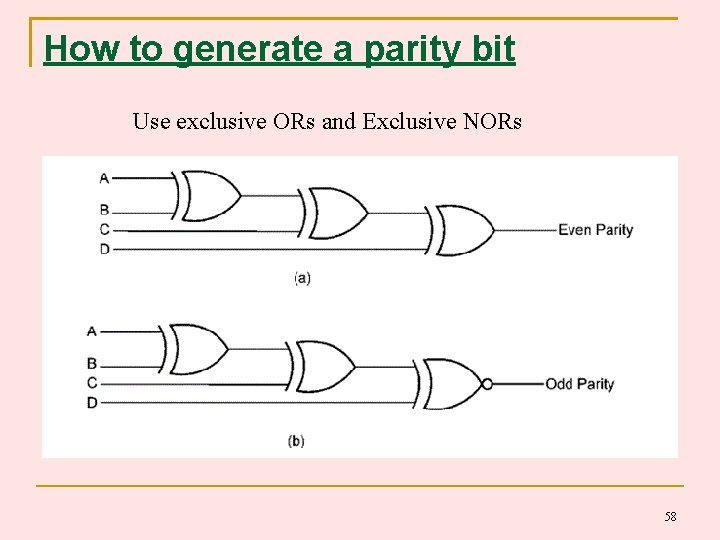
How to generate a parity bit Use exclusive ORs and Exclusive NORs 58

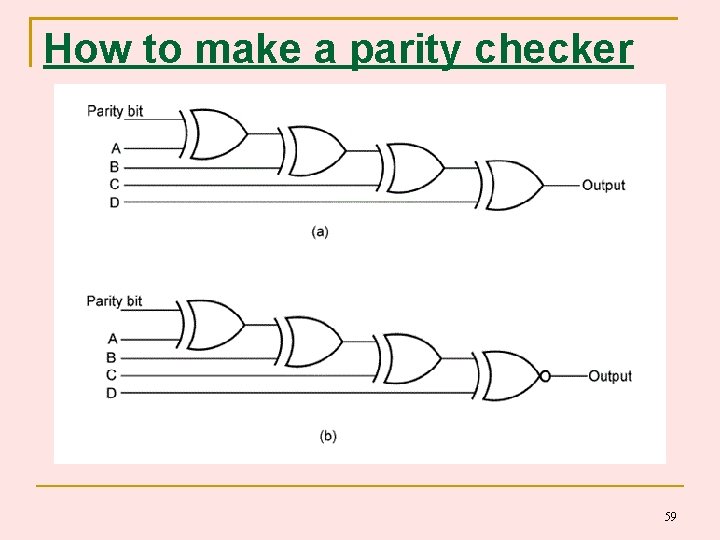
How to make a parity checker 59

Odd or even parity ~ 0 out of a parity checker means the parity checks and all is ok ~ 1 out of a parity checker means there is an error 60

ﺍﻟﻤﻤﻠﻜﺔ ﺍﻟﻌﺮﺑﻴﺔ ﺍﻟﺴﻌﻮﺩﻳﺔ ﻭﺯﺍﺭﺓ ﺍﻟﺘﻌﻠﻴﻢ ﺟﺎﻣﻌﺔ ﺃﻢ ﺍﻟﻘﺮﻯ ﺍﻟﻜﻠﻴﺔ ﺍﻟﺠﺎﻣﻌﻴﺔ ﺃﻀﻢ ﻗﺴﻢ ﺍﻟﺤﺎﺳﺐ ﺍﻵﻠﻲ Kingdom of Saudi Arabia Ministry of Education Umm Al. Qura University Adam University College Computer Science Department This Summary is an Online Content from this Book: Morris Mano, DIGITAL DESIGN, 4 th Edition, Prentice Hall, 2007 It is edited for Logic Analysis and Design Course 68032133 by: T. Mariah Sami Khayat Teacher Assistant @ Adam University College For Contacting: mskhayat@uqu. edu. sa 61