Digital Logic Design Chapter 3 Digital Systems and

Digital Logic Design Chapter 3 Digital Systems and Binary Numbers Al-Mustansiriyah University College of Science Computer Department Dr. Ghassan M. Al-Saddi

Outline of Chapter 3 © 3. 1 Simplification of Boolean Functions © 3. 2 Product of Sum simplification © 3. 3 Don’t- Care Condition

Another method of simplification of Boolean function is Karnaugh – Map (K-Map). This map is a diagram made of squares, each square represent one minterms, and there are several types of K-|Map depending on the number of variables in Boolean function.

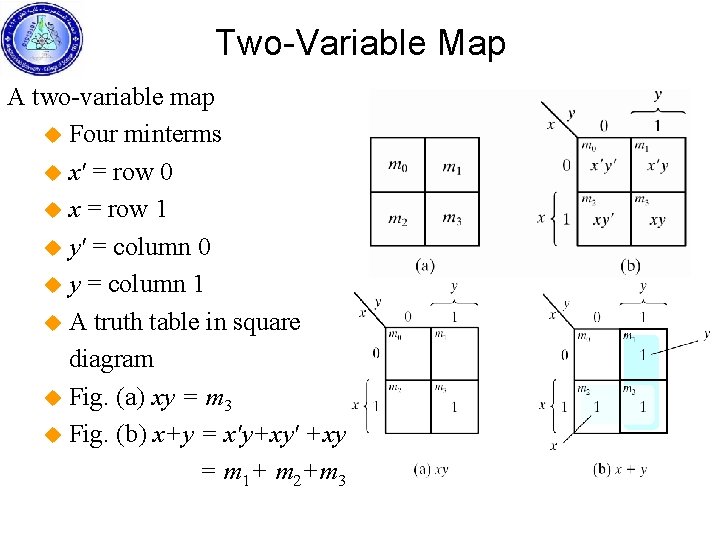
Two-Variable Map A two-variable map u Four minterms u x' = row 0 u x = row 1 u y' = column 0 u y = column 1 u A truth table in square diagram u Fig. (a) xy = m 3 u Fig. (b) x+y = x'y+xy' +xy = m 1+ m 2+m 3

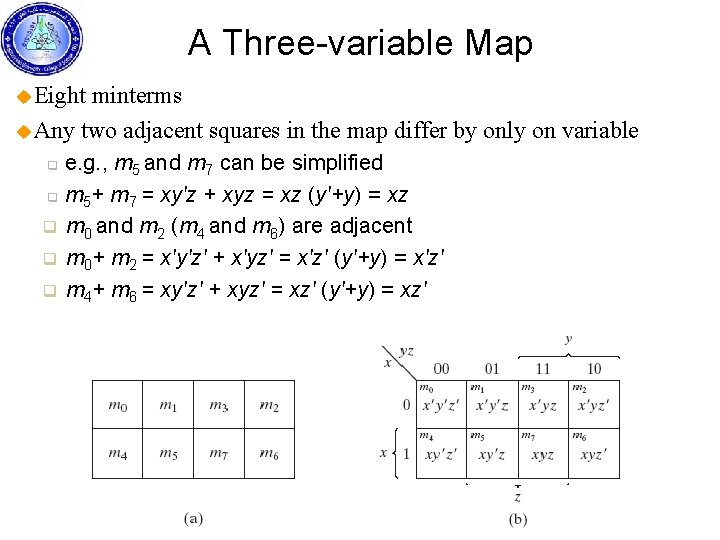
A Three-variable Map u Eight minterms u Any two adjacent squares in the map differ by only on variable q q q e. g. , m 5 and m 7 can be simplified m 5+ m 7 = xy'z + xyz = xz (y'+y) = xz m 0 and m 2 (m 4 and m 6) are adjacent m 0+ m 2 = x'y'z' + x'yz' = x'z' (y'+y) = x'z' m 4+ m 6 = xy'z' + xyz' = xz' (y'+y) = xz'

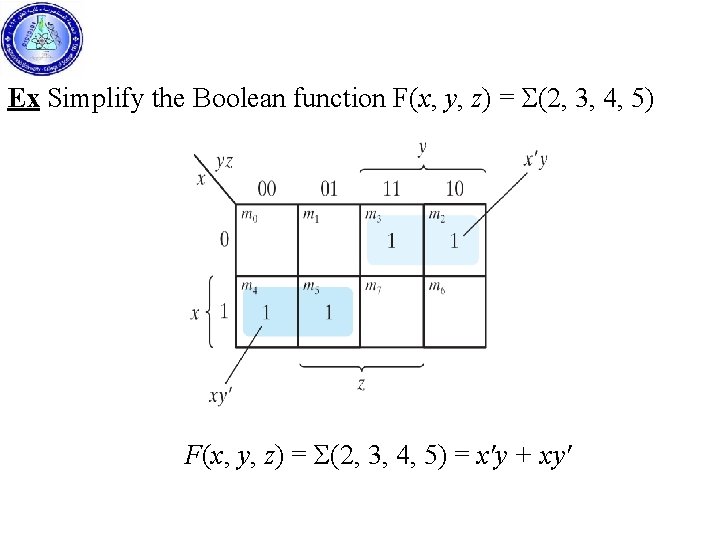
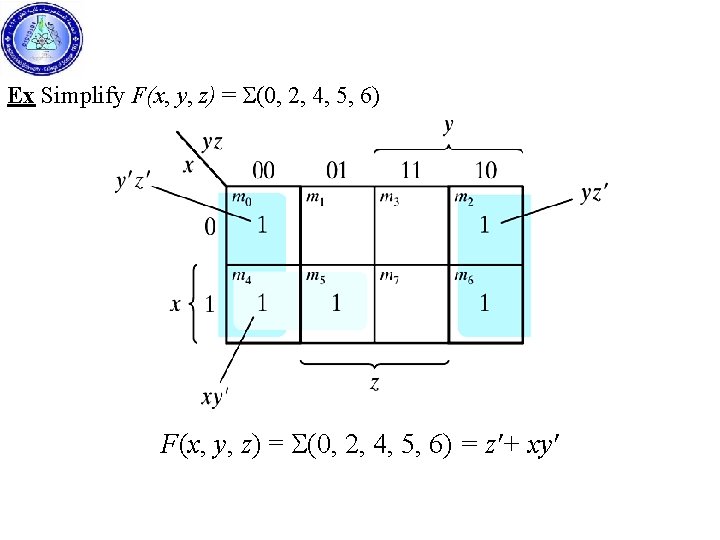
Ex Simplify the Boolean function F(x, y, z) = S(2, 3, 4, 5) F(x, y, z) = Σ(2, 3, 4, 5) = x'y + xy'

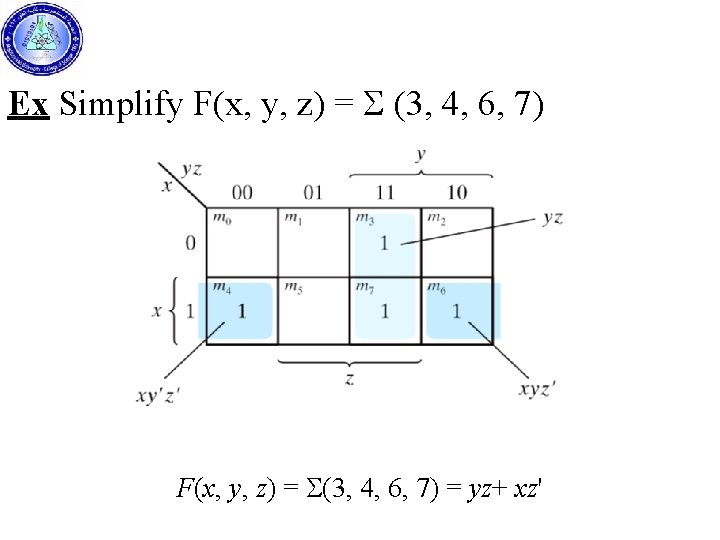
Ex Simplify F(x, y, z) = S (3, 4, 6, 7) F(x, y, z) = S(3, 4, 6, 7) = yz+ xz'

Four adjacent Squares Consider four adjacent squares um 0+m 2+m 4+m 6= x'y'z'+x'yz'+xy'z'+xyz' =x'z'(y'+y) +xz'(y'+y)= x'z' + xz‘= z' um 1+m 3+m 5+m 7 = x'y'z+x'yz+xy'z+xyz =x'z(y'+y) + xz(y'+y) =x'z + xz = z

Ex Simplify F(x, y, z) = S(0, 2, 4, 5, 6) = z'+ xy'

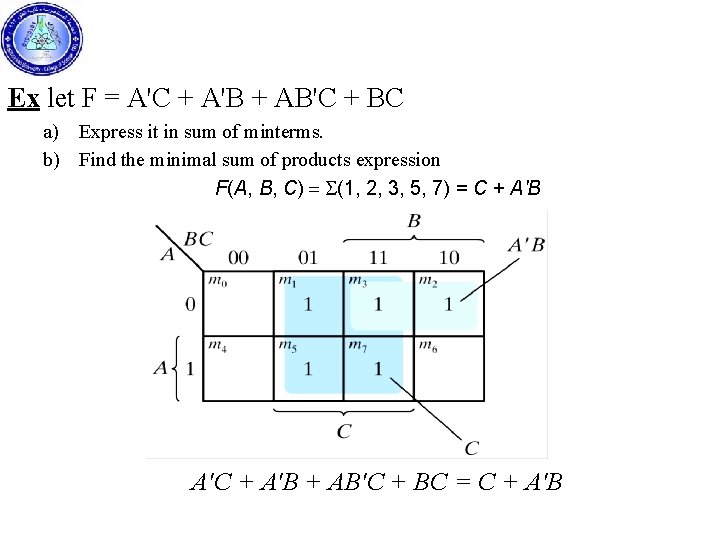
Ex let F = A'C + A'B + AB'C + BC a) Express it in sum of minterms. b) Find the minimal sum of products expression F(A, B, C) = S(1, 2, 3, 5, 7) = C + A'B A'C + A'B + AB'C + BC = C + A'B

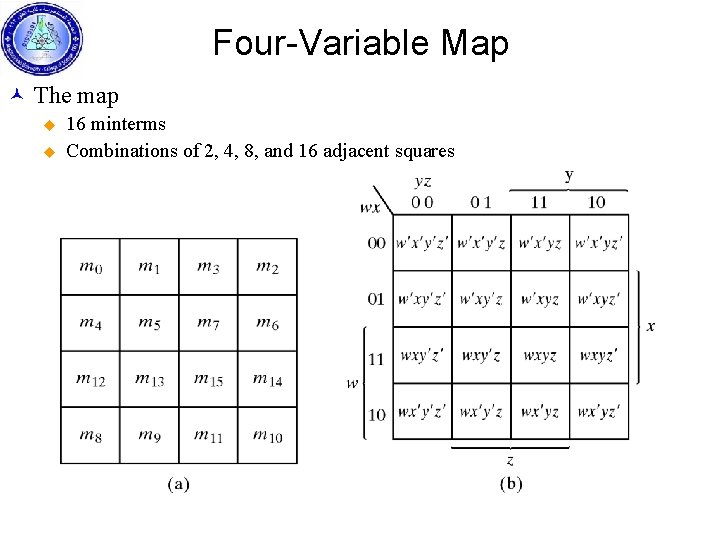
Four-Variable Map © The map u u 16 minterms Combinations of 2, 4, 8, and 16 adjacent squares

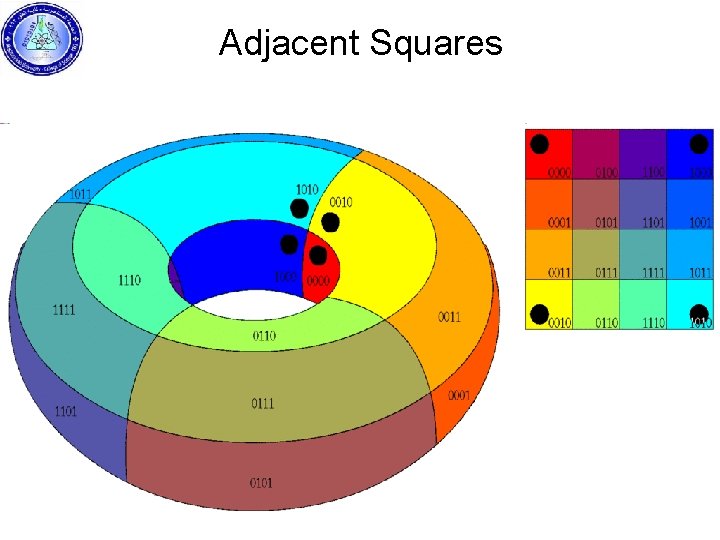
Adjacent Squares

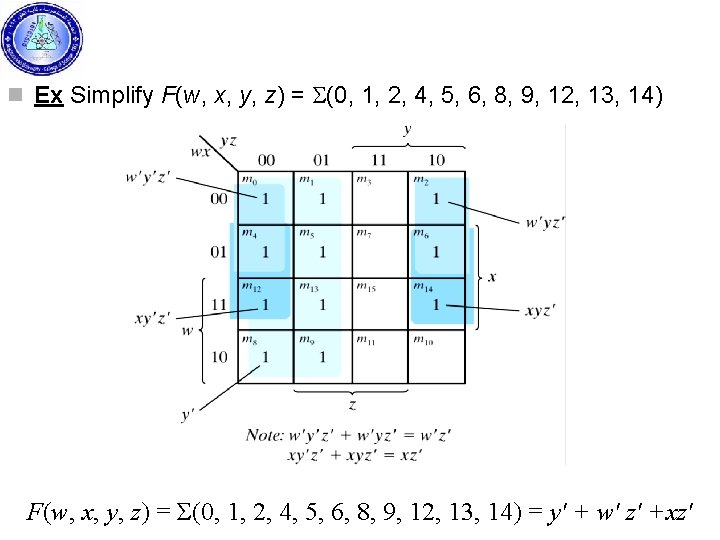
n Ex Simplify F(w, x, y, z) = S(0, 1, 2, 4, 5, 6, 8, 9, 12, 13, 14) F(w, x, y, z) = Σ(0, 1, 2, 4, 5, 6, 8, 9, 12, 13, 14) = y' + w' z' +xz'

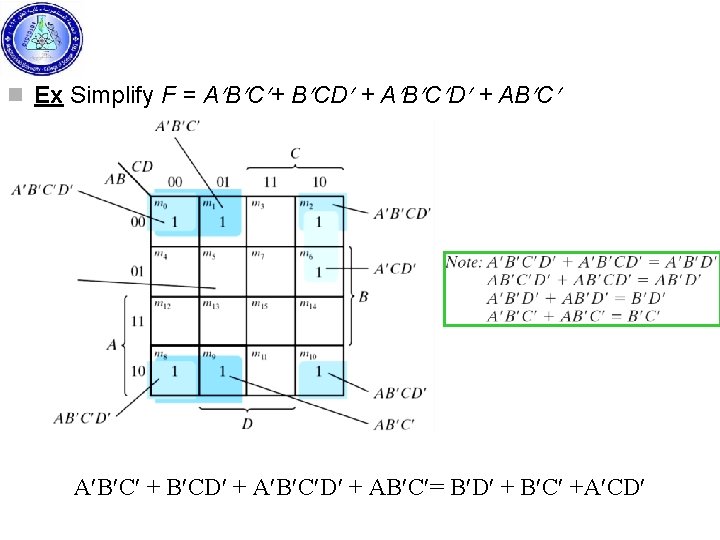
n Ex Simplify F = A B C + B CD + A B C D + AB C = B D + B C +A CD

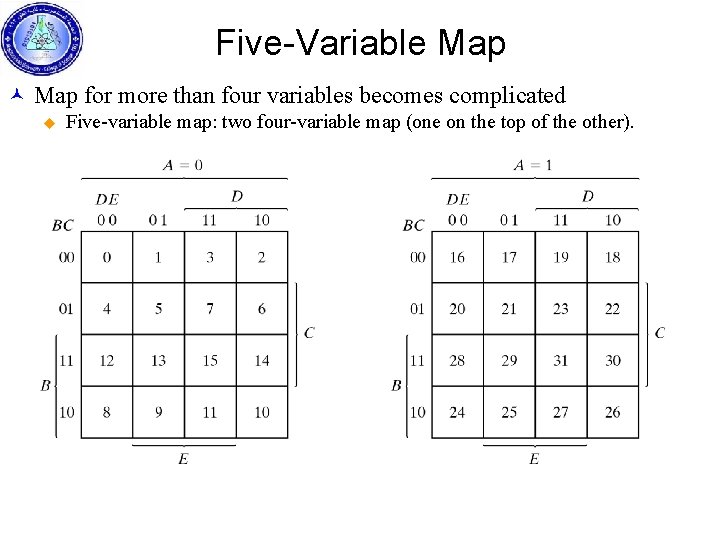
Five-Variable Map © Map for more than four variables becomes complicated u Five-variable map: two four-variable map (one on the top of the other).

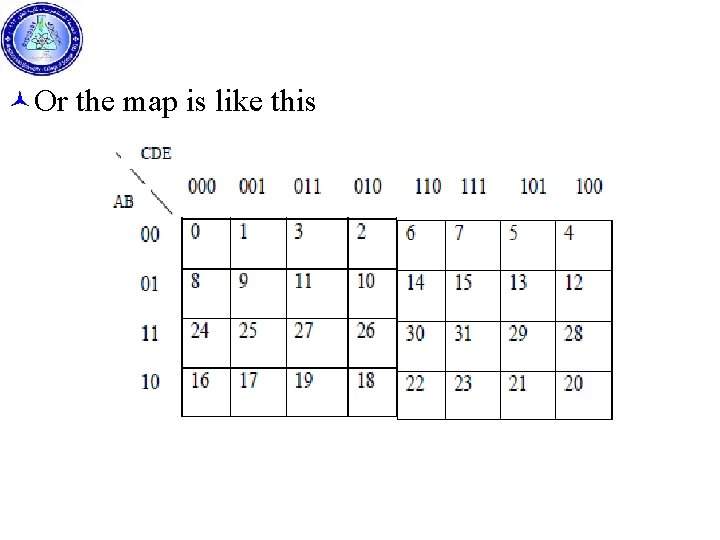
© Or the map is like this

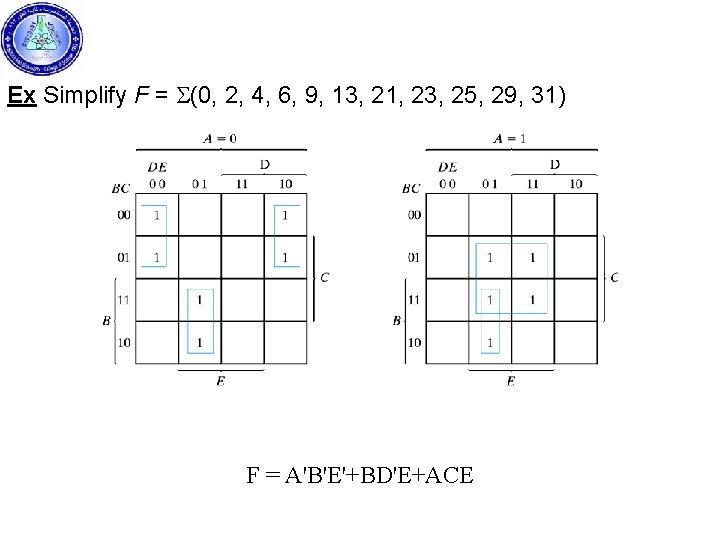
Ex Simplify F = S(0, 2, 4, 6, 9, 13, 21, 23, 25, 29, 31) F = A'B'E'+BD'E+ACE

Ex Simply the following Boolean functions using K –Map? 1 - F = X Y Z + X Y Z F = X Y + X Y 2 - F = X Y Z + X Y Z F = Y Z + X Z 3 - F = A C + A B C + B C F = C + A B 4 - F ( X, Y, Z ) = Σ ( 0, 2, 4 , 5 , 6 ) F ( X, Y, Z ) = Z + X Y 5 - F ( X, Y, Z, W ) = Σ ( 0, 1, 2, 4, 5, 6, 8 , 9 , 12, 13, 14 ) F ( X, Y, Z, W ) = Z + X W + Y W 6 - F = A B C + B C D + A B C F ( A, B, C, D ) = B D + B C + A C D

H. W Simplify the following functions in sum of product using Kmap 1 - F = X Y + X Y W + W ( X Y + X Y ) 2 - F = A B D + A C D + A B D 3 - F ( A, B , C, D ) = Π ( 2, 3, 6, 7, 8, 9, 10 , 11, 12, 13, 14 )

Product of Sum simplification In previous examples the simplification in Sum of Product form and each minterms represented by 1 (one) in K-map and each missing term in the function is a complement of the function and represented by 0 (zero) in k-map and the simplified expression obtained F (the complement of the function).

Sum-of-Minterm Procedure n Consider the function defined in Table; q In sum-of-minterm: q In sum-of-maxterm: q Taking the complement of F

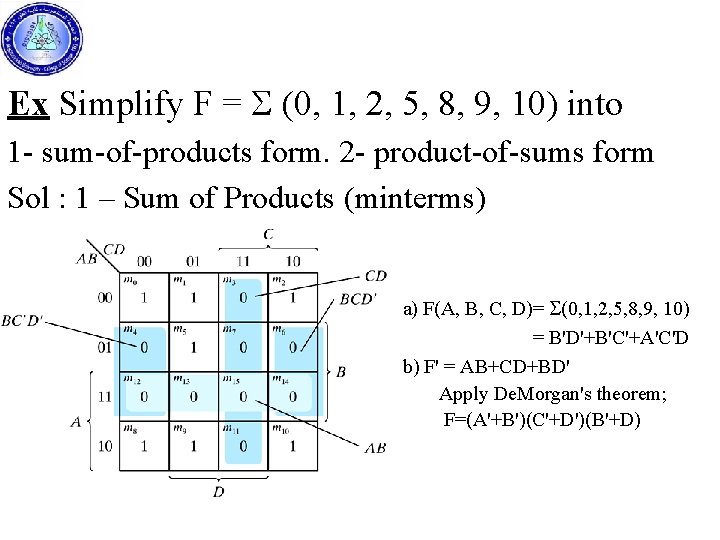
Ex Simplify F = S (0, 1, 2, 5, 8, 9, 10) into 1 - sum-of-products form. 2 - product-of-sums form Sol : 1 – Sum of Products (minterms) a) F(A, B, C, D)= S(0, 1, 2, 5, 8, 9, 10) = B'D'+B'C'+A'C'D b) F' = AB+CD+BD' Apply De. Morgan's theorem; F=(A'+B')(C'+D')(B'+D)

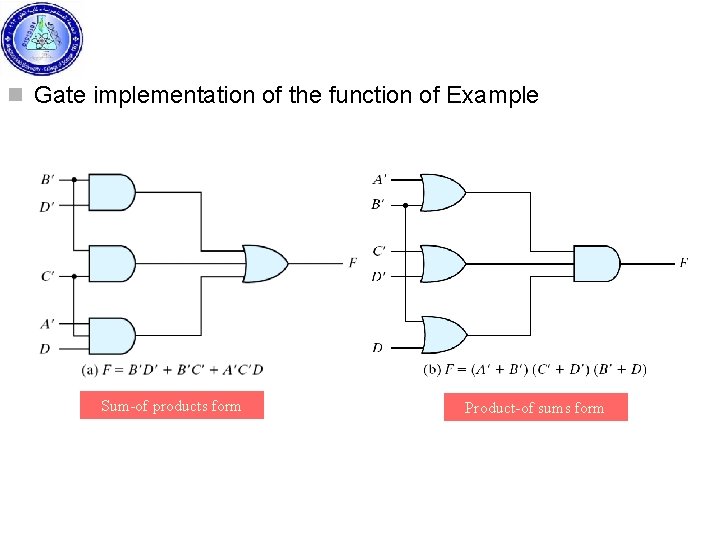
n Gate implementation of the function of Example Sum-of products form Product-of sums form

Ex Obtained the simplified expression in Product of Sums F = ( A' + B' + D ) ( A' + D' ) ( A + B' + C + D ) F' = A B D' + A D + A' B' D + A' B C' D' CD AB 00 01 11 10 00 01 0 0 11 0 0 10 0 F' = A B + B' D + B C' D' F = ( A' + B' ) ( B + D' ) ( B' + C + D )

Ex Obtained the simplified expression in Product of Sums F ( A, B, C, D ) = Π ( 0, 1, 2, 3, 4, 10, 11) CD AB 00 00 01 0 10 01 11 0 0 10 0 F' = A' B' + A' C' D' + B' C F = ( A + B ) ( A + C + D ) ( B + C' )

H. W : Obtained the simplified expression of the following functions in 1 - Sum of Products 2 - Product of Sums 1 - F = X' Y' + Y' Z' + Y Z' + X Y Z 2 - F ( X, Y, Z, W) = Π ( 1, 3 , 5, 7, 13, 15 ) 3 - F = ( A + B' + D ) ( A' + B + D) ( C + D ) ( C' + D' )

Don't-Care Conditions © The “Don’t Care” conditions allow to replace the empty cell of a K-Map to form a grouping of the variables. © While forming groups of cells, we can consider a “Don’t Care” cell as either 1 or 0 or we can simply ignore that cell. © Therefore, “Don’t Care” condition can help to form a larger group of cells. © A Don’t Care cell can be represented by a cross(X) in K-Maps representing a invalid combination. © These values used in simplification with F and F'.

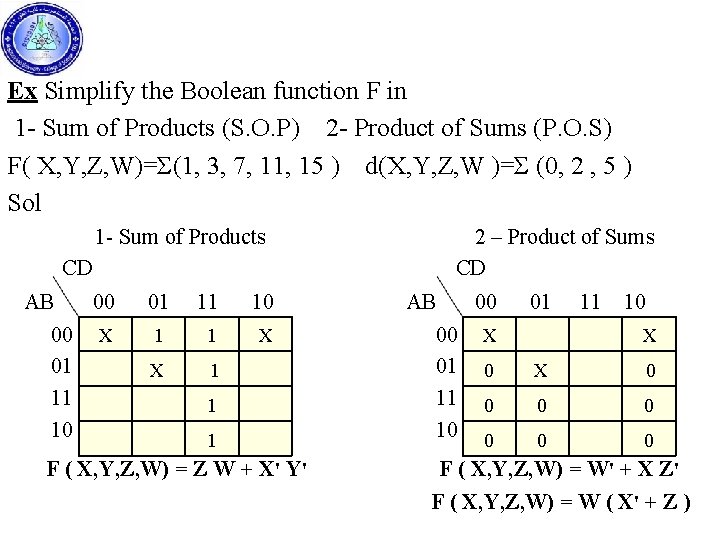
Ex Simplify the Boolean function F in 1 - Sum of Products (S. O. P) 2 - Product of Sums (P. O. S) F( X, Y, Z, W)=Σ(1, 3, 7, 11, 15 ) d(X, Y, Z, W )=Σ (0, 2 , 5 ) Sol 1 - Sum of Products CD AB 00 00 X 01 11 10 1 1 X X 1 1 1 F ( X, Y, Z, W) = Z W + X' Y' 2 – Product of Sums CD AB 00 00 X 01 0 10 0 01 11 10 X X 0 0 0 F ( X, Y, Z, W) = W' + X Z' F ( X, Y, Z, W) = W ( X' + Z )

Ex Simplify the Boolean function F in 1 - Sum of Products 2 - Product of Sums using don’t care condition F = A C E + A' C D' E' + A' C' D E D = D E' + A' D' E + A D' E' Sol F = A C E. 1 + A C D E = A C D E + A C D' E + A' C D' E' + A' C' D E D = D E' ( A + A' ) + A' D' E ( C + C' ) + A D' E' ( C + C' ) = A D E' ( C + C' ) + A' C D' E + A' C' D' E + A C D' E' + A C' D' E' = A C D E' + A C' D E' + A' C D' E + A' C' D' E +A C D' E' + A C' D' E'

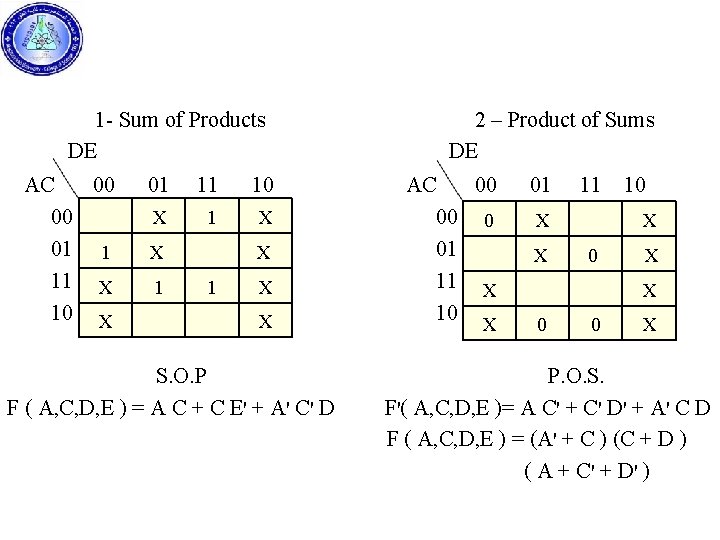
1 - Sum of Products DE AC 00 00 01 1 11 X 10 X 01 11 10 X 1 X 1 X X S. O. P F ( A, C, D, E ) = A C + C E' + A' C' D 2 – Product of Sums DE AC 00 00 0 01 11 X 10 X 01 11 X X 10 X X 0 0 X P. O. S. F'( A, C, D, E )= A C' + C' D' + A' C D F ( A, C, D, E ) = (A' + C ) (C + D ) ( A + C ' + D' )

H. W. Simplify the Boolean function F in Sum of Products using don’t care condition F = B' C' D' + B C D' + A B C' D D = B' C D' + A' B C' D'