Digital Logic Design Chapter 1 Part a Digital

Digital Logic Design Chapter 1 (Part a) Digital Systems and Binary Numbers Originally by T. Tasniem Nasser Al-Yahya

Outline of Chapter 1 (Part a) © 1. 1 Digital Systems © 1. 2 Binary Numbers © 1. 3 Number-base Conversions © 1. 4 Octal and Hexadecimal Numbers

Outline of Chapter 1 (Part a) © 1. 1 Digital Systems © 1. 2 Binary Numbers © 1. 3 Number-base Conversions © 1. 4 Octal and Hexadecimal Numbers

Digital Systems © Digital systems (systems that can manipulate Discrete information) u u Digital Computers. Digital camera. Electronic calculators. Digital TV.

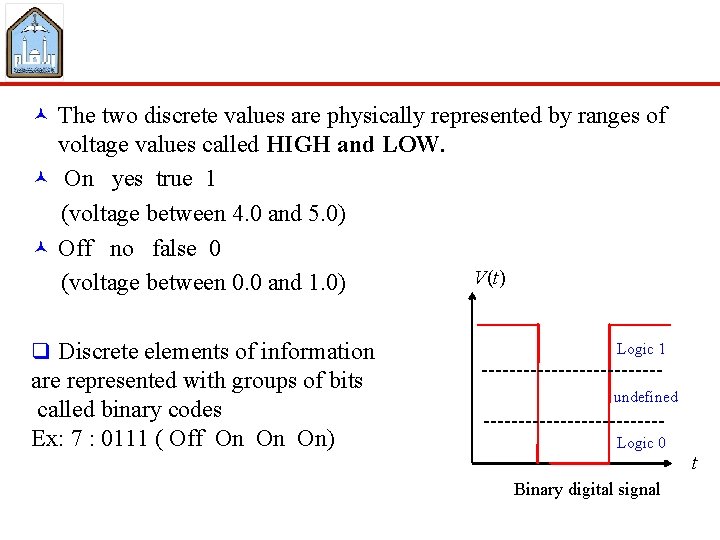
Analog and Digital Signal © In digital system, discrete element of information are represented by quantities called signals. © Analog Signal u u The physical quantities may vary continuously over a specified range. (infinite possible values). Ex: voltage on a wire created by microphone © Digital Signal. u u a digital signal has discrete values over a specified range Ex: button pressed on a keyboard. X (t) Digital signal Analog signal t

© The signals in most digital systems use just two discrete values and therefore said to be binary. © A binary digit , called a bit, has two values : 0 and 1.

© The two discrete values are physically represented by ranges of voltage values called HIGH and LOW. © On yes true 1 (voltage between 4. 0 and 5. 0) © Off no false 0 (voltage between 0. 0 and 1. 0) q Discrete elements of information are represented with groups of bits called binary codes Ex: 7 : 0111 ( Off On On On) V(t) Logic 1 undefined Logic 0 Binary digital signal t

© A digital system is an interconnection of digital modules © To understand the operation of each digital module , it is necessary to have a basic knowledge of digital circuits and their logical functions.

Outline of Chapter 1 © 1. 1 Digital Systems © 1. 2 Binary Numbers © 1. 3 Number-base Conversions © 1. 4 Octal and Hexadecimal Numbers

Decimal Number System © Base (also called radix) = 10 u 10 digits { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } © Coefficient Position u Integer & fraction © Coefficient Weight u Weight = (Base) Position © In general Magnitude: u 2 1 0 5 1 2 100 -1 -2 7 4 10 1 0. 01 10 2 0. 7 0. 04 Sum of “Coefficient x Weight” 500 a 2*r 2+a 1*r 1+a 0*r 0+a-1*r-1+a-2*r-2 (512. 74)10

General positional Number System © Base (also called radix) = r u u u r is an integer and ≥ 2 r digits { 0, …. . , r-1} (546)4 is not correct © Coefficient Weight u Weight = (Base) Position=i © Magnitude (The value of a digit depends not only on its value but also on its position within the number. u The magnitude M of a number ( ) in base r is:

Binary Number System © Base = 2 u 2 digits { 0, 1 }, called binary digits or “bits” 4 © Weights u Weight = (Base) Position © Magnitude u Sum of “Bit x Weight” © Formal Notation © Groups of bits u 4 bits = Nibble u 8 bits = Byte 1011 11000101 2 1 1/2 1/4 1 0 1 2 -1 1 0 -2 2 1 0 -1 1 *2 +0 *2 +1 *2 2 =(5. 25)10 (101. 01)2

Binary Arithmetic Operations The next section will discuss Unsigned arithmetic operations in Unsigned Binary base system © Addition © Subtraction © Multiplication

Addition © The sum of two binary numbers is calculated by the same rules as in decimal except that the digits of the sum in any significant position can be only zero or one © Line up the numbers from right to left. If one number is shorter extend it by adding leading zeros to the number. (the extension is different with signed number) © Work from right to left – add each pair of digits together with carry propagation. 0+0=0 0+1=1 1+0=1 1+1=01 ( carry ) 1+1+1=11 (carry)

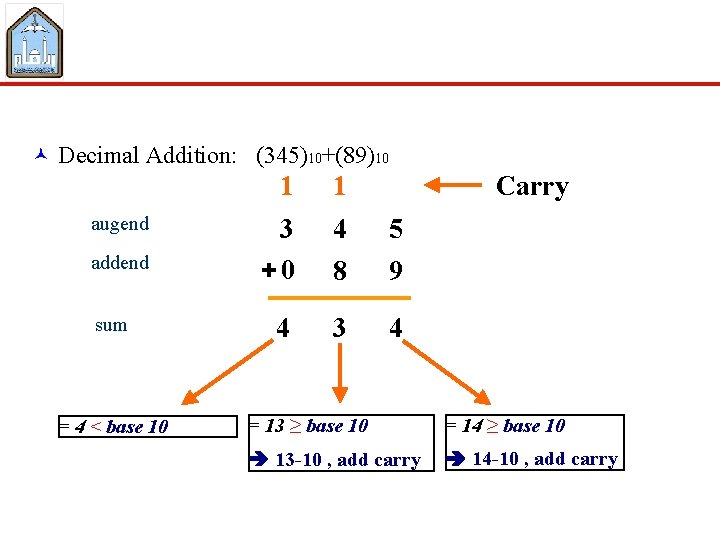
© Decimal Addition: (345)10+(89)10 augend addend sum = 4 < base 10 1 1 Carry 3 +0 4 5 8 9 4 3 4 = 13 ≥ base 10 = 14 ≥ base 10 13 -10 , add carry 14 -10 , add carry

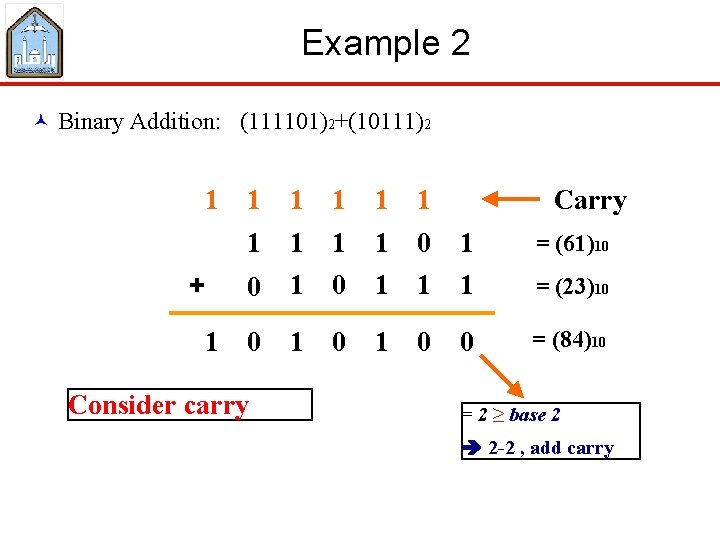
Example 2 © Binary Addition: (111101)2+(10111)2 1 + 1 Carry 1 1 1 1 1 0 1 = (61)10 0 1 1 1 = (23)10 0 1 0 0 = (84)10 Consider carry = 2 ≥ base 2 2 -2 , add carry

Binary Addition © Practice Calculate (101101)2+(100111)2

Subtraction © Line up the numbers from right to left. If one number is shorter extend it by adding leading zeros to the number. © Work from right to left –Subtract each pair of digits together with borrowing where needed 0 -0=0 0 -1=1 (after borrowing) 1 -0=1 1 -1=0

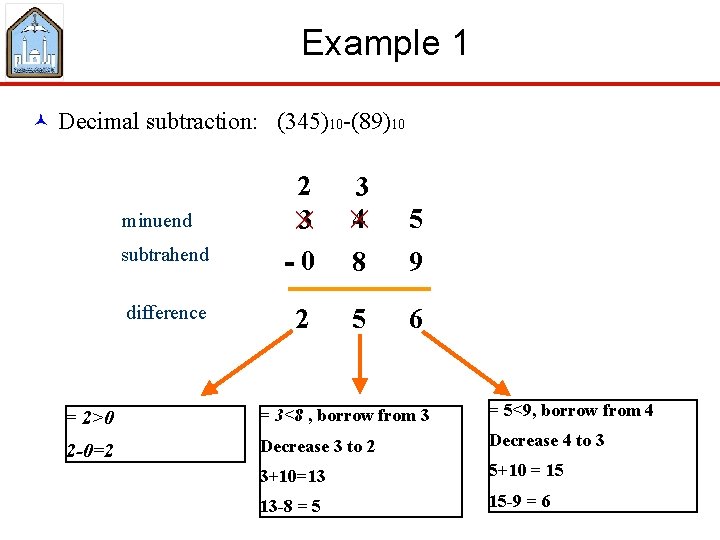
Example 1 © Decimal subtraction: (345)10 -(89)10 minuend subtrahend difference 2 3 -0 3 4 × × 5 8 9 2 5 6 = 2>0 = 3<8 , borrow from 3 = 5<9, borrow from 4 2 -0=2 Decrease 3 to 2 Decrease 4 to 3 3+10=13 5+10 = 15 13 -8 = 5 15 -9 = 6

Example 2 © Binary subtraction : (111101)2 -(10111)2 1 - 1 1 1 0 1 = (61)10 0 1 1 1 = (23)10 1 1 0 = (38)10 0

Binary Subtraction © Practice Calculate (101101)2 -(100111)2

Binary Subtraction © In many cases binary subtraction is done in a special way by binary addition. Why? © It is much more simple to do it that way. �� One simple building block called adder can be implemented and used for both binary addition and subtraction. © This subject will be discussed later

Multiplication © Multiplication is Simple. © The multiplier digits are always 1 or 0, therefore , the partial products are equal either to the multiplicand or to 0 0*0=0 0*1=0 1*0=0 1*1=1

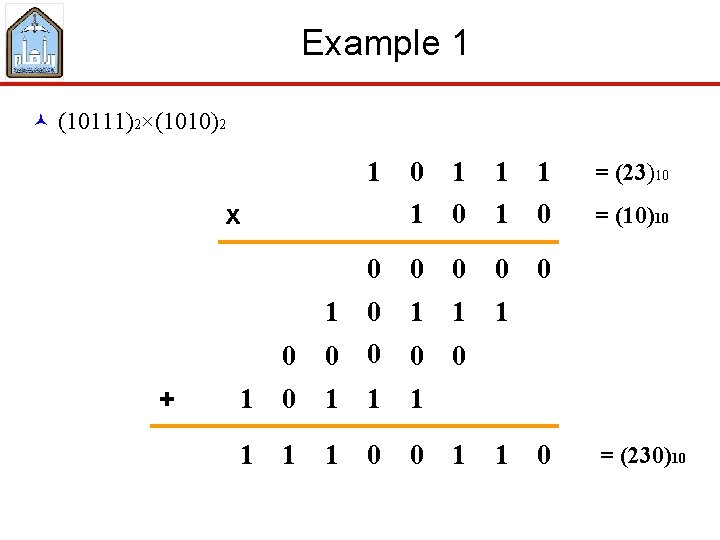
Example 1 © (10111)2×(1010)2 1 0 1 1 1 = (23)10 1 0 = (10)10 0 0 1 0 1 1 1 0 0 0 1 1 1 1 0 0 x + 1 1 0 = (230)10

Binary Multiplication © Practice Calculate (1011)2 * (101)2

Recall : Decimal Number System © Base (also called radix) = 10 u 10 digits { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } © Coefficient Position u Integer & fraction © Coefficient Weight u Weight = (Base) Position © In general Magnitude: u 2 1 0 5 1 2 100 -1 -2 7 4 10 1 0. 01 10 2 0. 7 0. 04 Sum of “Coefficient x Weight” 500 a 2*r 2+a 1*r 1+a 0*r 0+a-1*r-1+a-2*r-2 (512. 74)10

Octal Number System © Base = 8 u 8 digits { 0, 1, 2, 3, 4, 5, 6, 7 } © Weights u Weight = (Base) Position © Magnitude u Sum of “Digit x Weight” 64 8 1 1/8 1/64 5 1 2 7 4 2 -1 1 0 -2 2 1 0 -1 5 *8 +1 *8 +2 *8 +7 *8 +4 *8 2 =(330. 9375)10 (512. 74)8 (Note that the digits 8 and 9 cannot appear in an octal number)

Hexadecimal Number System © Base = 16 u u 16 digits { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F } Where A=10 B=11 C=12 D=13 E= 14 F=15 © Weights u Weight = (Base) Position © Magnitude u Sum of “Digit x Weight” 256 16 1 1/16 1/256 1 E 5 7 A 2 -1 1 0 -2 1 *162+14 *161+5 *160+7 *16 -1+10 *16 -2 =(485. 4765625)10 (1 E 5. 7 A)16

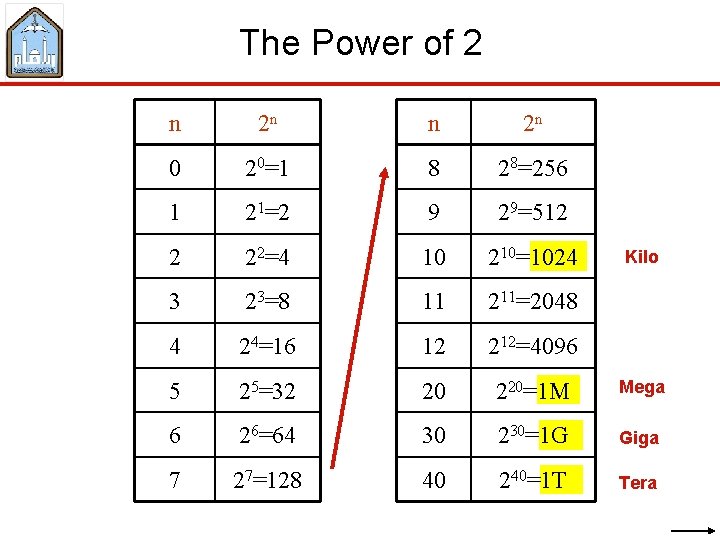
The Power of 2 n 2 n 0 20=1 8 28=256 1 21=2 9 29=512 2 22=4 10 210=1024 3 23=8 11 211=2048 4 24=16 12 212=4096 5 25=32 20 220=1 M Mega 6 26=64 30 230=1 G Giga 7 27=128 40 240=1 T Tera Kilo

Outline of Chapter 1 © 1. 1 Digital Systems © 1. 2 Binary Numbers © 1. 3 Number-base Conversions © 1. 4 Octal and Hexadecimal Numbers

Outline of Chapter 1 © 1. 4 Octal and Hexadecimal Numbers © 1. 3 Number-base Conversions

Octal and Hexadecimal Numbers © The conversion from and to binary , octal , and hexadecimal plays an important role in digital computers © Digital computers use binary numbers. However , they are difficult to work with as they are long. © By using octal or hexadecimal conversion , the human operator thinks in terms of octal and hex numbers and performs the required conversion when direct information with the machine is necessary.

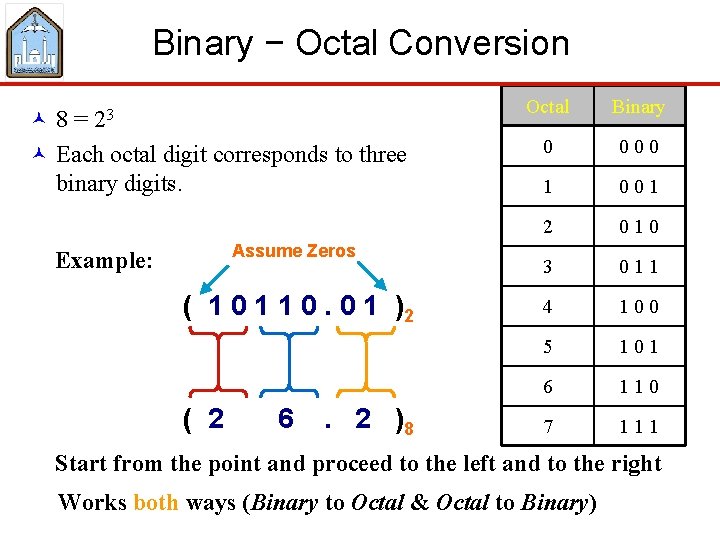
Binary − Octal Conversion © 8 = 23 © Each octal digit corresponds to three binary digits. Assume Zeros Example: ( 1 0 1 1 0. 0 1 )2 ( 2 6 . 2 )8 Octal Binary 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 Start from the point and proceed to the left and to the right Works both ways (Binary to Octal & Octal to Binary)

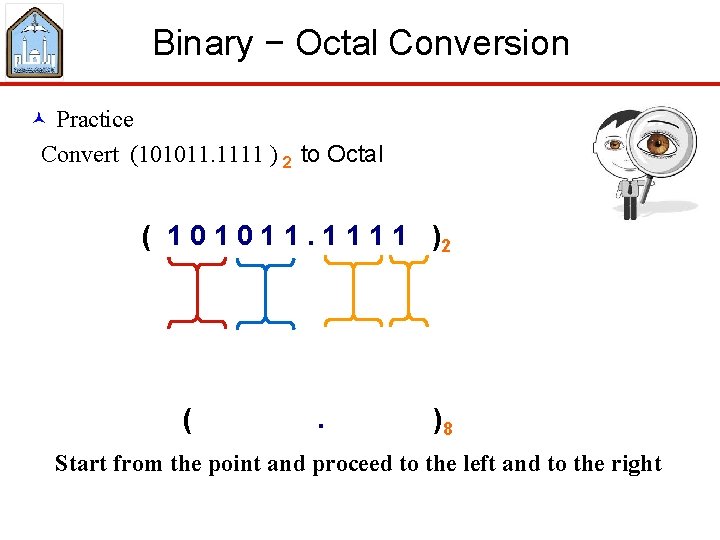
Binary − Octal Conversion © Practice Convert (101011. 1111 ) 2 to Octal ( 1 0 1 1 )2 ( . )8 Start from the point and proceed to the left and to the right

Binary − Hexadecimal Conversion © 16 = 24 © Each hexadecimal digit corresponds to four binary digits Assume Zeros Example: ( 1 0 1 1 0. 0 1 )2 (1 6 . 4 )16 Hex Binary 0 1 2 3 4 5 6 7 8 9 A B C D E F 0 0 0 0 1 1 0 0 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 0 1 1 Works both ways (Binary to Hex & Hex to Binary)

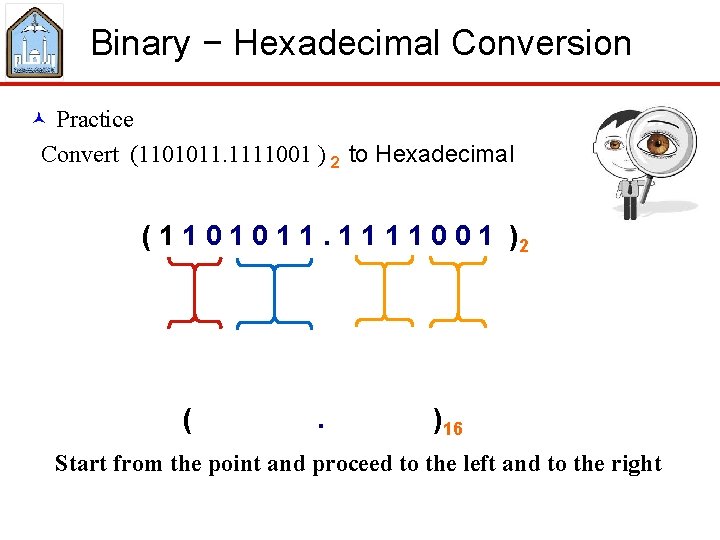
Binary − Hexadecimal Conversion © Practice Convert (1101011. 1111001 ) 2 to Hexadecimal ( 1 1 0 1 1 0 0 1 )2 ( . )16 Start from the point and proceed to the left and to the right

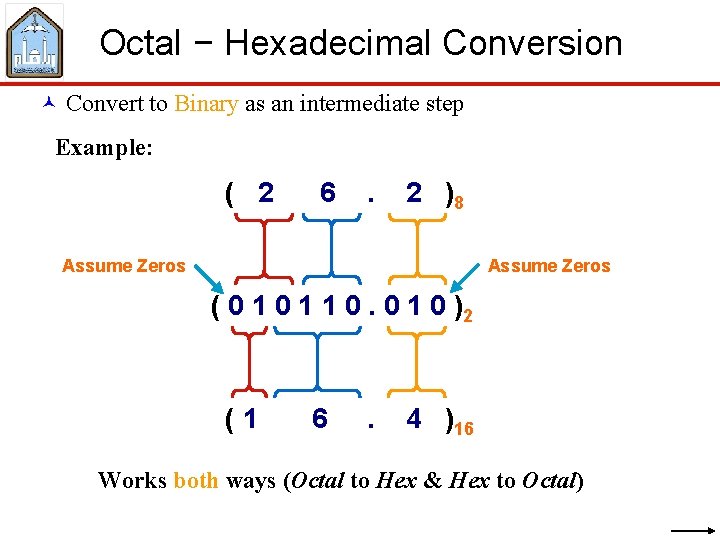
Octal − Hexadecimal Conversion © Convert to Binary as an intermediate step Example: ( 2 6 . 2 )8 Assume Zeros ( 0 1 1 0. 0 1 0 )2 (1 6 . 4 )16 Works both ways (Octal to Hex & Hex to Octal)

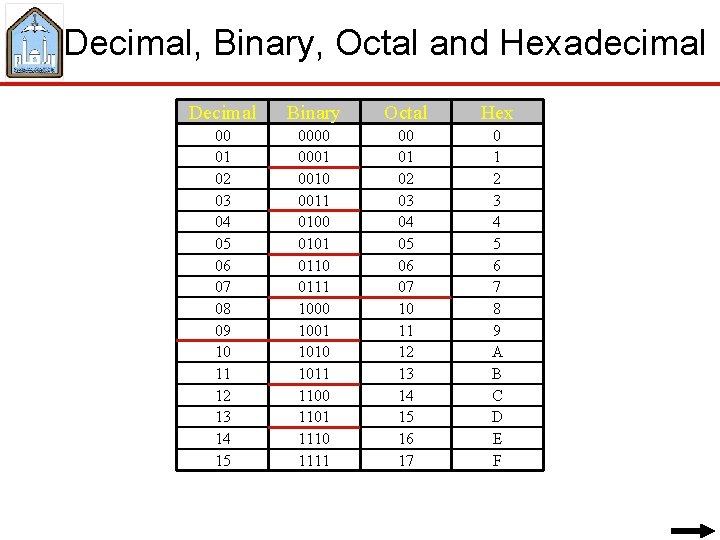
Decimal, Binary, Octal and Hexadecimal Decimal Binary Octal Hex 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 00 01 02 03 04 05 06 07 10 11 12 13 14 15 16 17 0 1 2 3 4 5 6 7 8 9 A B C D E F

Outline of Chapter 1 © 1. 4 Octal and Hexadecimal Numbers © 1. 3 Number-base Conversions

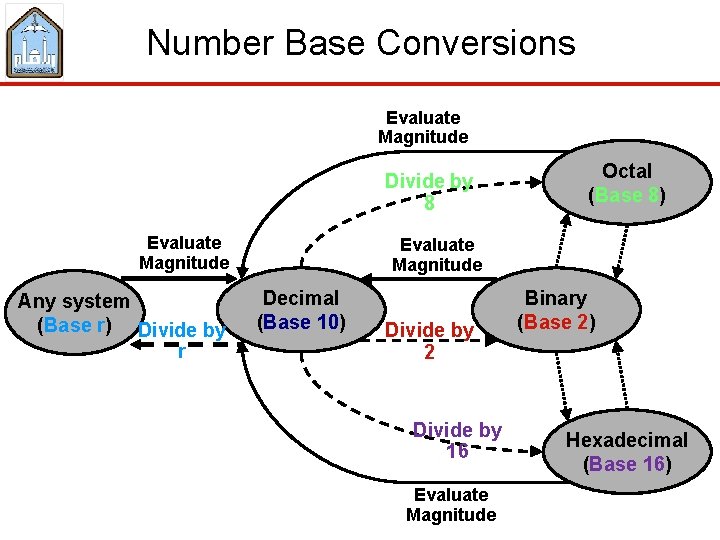
Number Base Conversions Evaluate Magnitude Divide by 8 Evaluate Magnitude Any system (Base r) Divide by r Octal (Base 8) Evaluate Magnitude Decimal (Base 10) Divide by 2 Divide by 16 Evaluate Magnitude Binary (Base 2) Hexadecimal (Base 16)

Conversion form any base to Decimal (Evaluate magnitude) Any system (Base r) Evaluate Magnitude Decimal (Base 10) © We can use the evaluate magnitude method to convert any base number to decimal. (see slide 9)

Conversion form any base to Decimal (Evaluate magnitude) © Example: convert 1101. 01 in binary to decimal: The decimal value is:

Conversion form Decimal to any base system (Divide by base) Any system (Base r) Divide by r Decimal (Base 10) © To convert a decimal integer into any base, keep dividing by r until the quotient is 0. Collect the remainders in reverse order. © To convert a fraction, keep multiplying the fractional part by r until it becomes 0 or until we reach the required accuracy. Collect the integer parts in forward order.

Decimal (Integer) to Binary Conversion © Divide the number by the ‘Base’ (=2) © Take the remainder (either 0 or 1) as a coefficient © Take the quotient and repeat the division until the quotient reaches zero. Example: (13)10 Quotient Remainder Coefficient 6 3 1 0 1 1 a 0 = 1 a 1 = 0 a 2 = 1 a 3 = 1 13/ 2 = 6 /2= 3 /2= 1 /2= Answer: (13)10 = (a 3 a 2 a 1 a 0)2 = (1101)2 MSB LSB MSB

Decimal (Fraction) to Binary Conversion © Multiply the number by the ‘Base’ (=2) © Take the integer (either 0 or 1) as a coefficient © Take the resultant fraction and repeat the division till you reach a zero or the required accuracy is attained. Example: (0. 625)10 Integer 0. 625 * 2 = 0. 5 *2= Answer: 1 0 1 . . . Fraction Coefficient 25 5 0 a-1 = 1 a-2 = 0 a-3 = 1 (0. 625)10 = (0. a-1 a-2 a-3)2 = (0. 101)2 MSB LSB

Decimal to Binary Conversion © Practice Convert (41. 6875 ) 10 to binary number © it is necessary to separate the number into an integer part and a fraction part, since each part must be converted differently.

Decimal to Octal Conversion Example: (175)10 Quotient 175 / 8 = 21 / 8 = 2 /8= Remainder Coefficient 7 5 2 a 0 = 7 a 1 = 5 a 2 = 2 21 2 0 Answer: (175)10 = (a 2 a 1 a 0)8 = (257)8 Example: (0. 3125)10 Integer 0. 3125 * 8 = 2 0. 5 *8= 4 Answer: . . Fraction Coefficient 5 0 a-1 = 2 a-2 = 4 (0. 3125)10 = (0. a-1 a-2 a-3)8 = (0. 24)8

Decimal to Octal Conversion © Practice Convert (153. 513 ) 10 to Octal number © it is necessary to separate the number into an integer part and a fraction part, since each part must be converted differently.

Decimal to Hexadecimal Conversion Example: (175)10 Quotient 175 / 16 = 10 / 16 = Remainder 15 10 10 0 Answer: Coefficient a 0 = F a 1 = A (175)10 = (a 1 a 0)16 = (AF)16 Example: (0. 3125)10 Integer 0. 3125 * 16 = Answer: 5 Fraction . 0 Coefficient a-1 = 2 (0. 3125)10 = (0. a-1)16 = (0. 2)16

© The following sections from chapter 1 have been given on the lecture but without power point slides 1. 5 , 1. 6, 1. 7