DIGITAL LOGIC DESIGN by Dr Fenghui Yao Tennessee

DIGITAL LOGIC DESIGN by Dr. Fenghui Yao Tennessee State University Department of Computer Science Nashville, TN Binary Systems 1

Digital Systems u They manipulate discrete information (A finite number of elements) Ø Example discrete sets ü u u 10 decimal digits, the 26 letters of alphabet Information is represented in binary form Examples Ø Ø Binary Systems Digital telephones, digital television, and digital cameras The most commonly used one is DIGITAL COMPUTERS 2

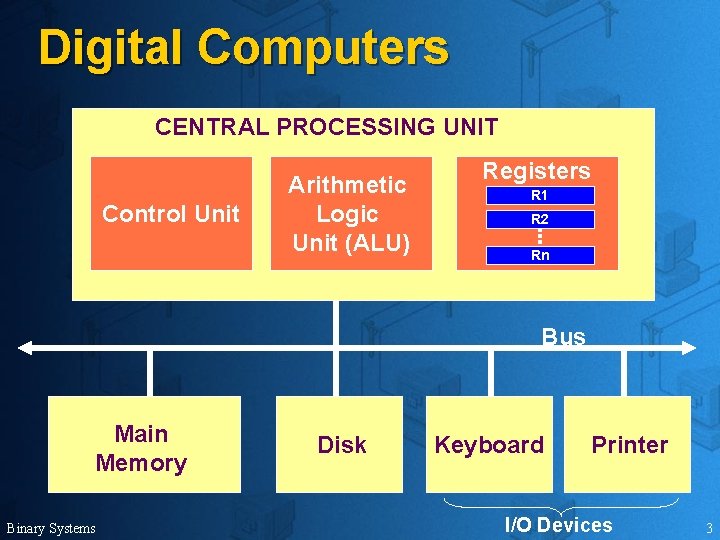
Digital Computers CENTRAL PROCESSING UNIT Control Unit Arithmetic Logic Unit (ALU) Registers R 1 R 2 Rn Bus Main Memory Binary Systems Disk Keyboard Printer I/O Devices 3

Binary Signals u It means two-states Ø Ø Ø u u 1 and 0 true and false on and off A single “on/off”, “true/false”, “ 1/0” is called a bit Example: Toggle switch Binary Systems 4

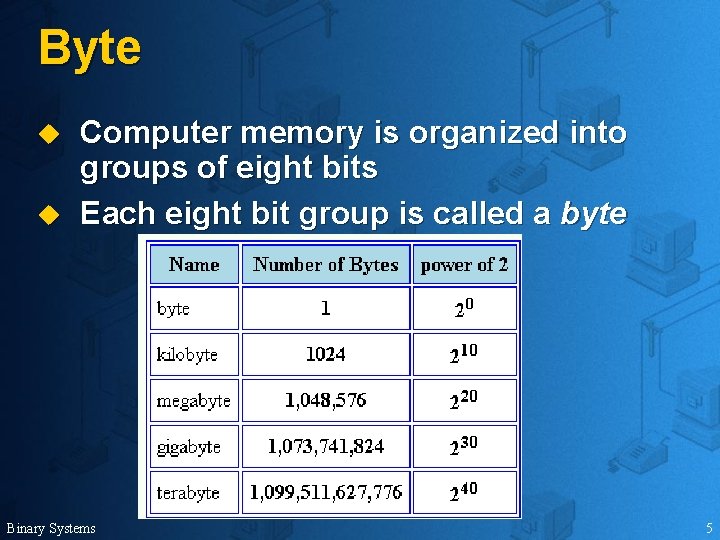
Byte u u Computer memory is organized into groups of eight bits Each eight bit group is called a byte Binary Systems 5

Why Computers Use Binary u They can be represented with a transistor that is relatively easy to fabricate (in silicon) Ø u Millions of them can be put in a tiny chip Unambiguous signal (Either 1 or 0) Ø Binary Systems This provides noise immunity 6

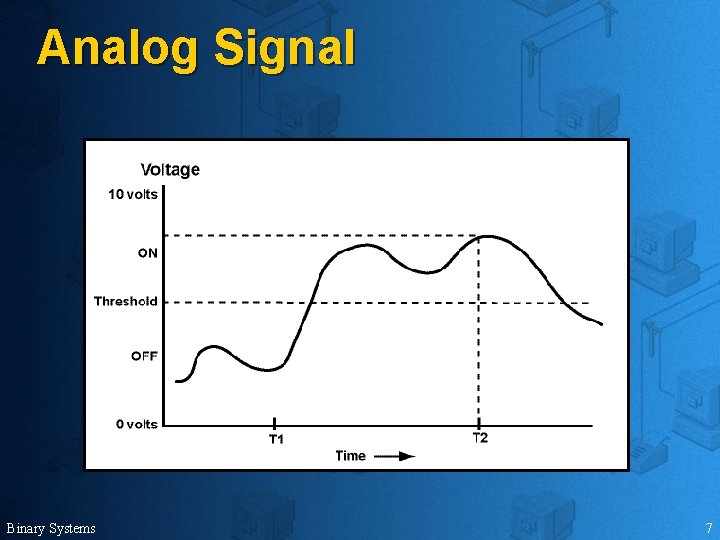
Analog Signal Binary Systems 7

Binary Signal u A voltage below the threshold Ø u off A voltage above threshold Ø Binary Systems on 8

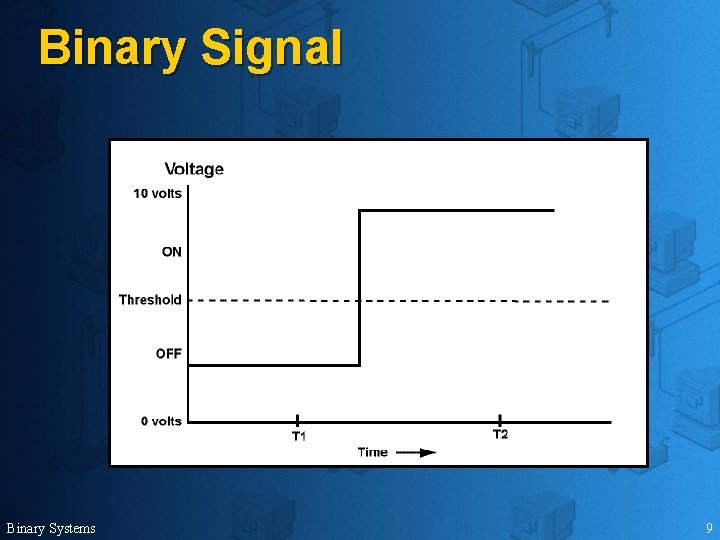
Binary Signal Binary Systems 9

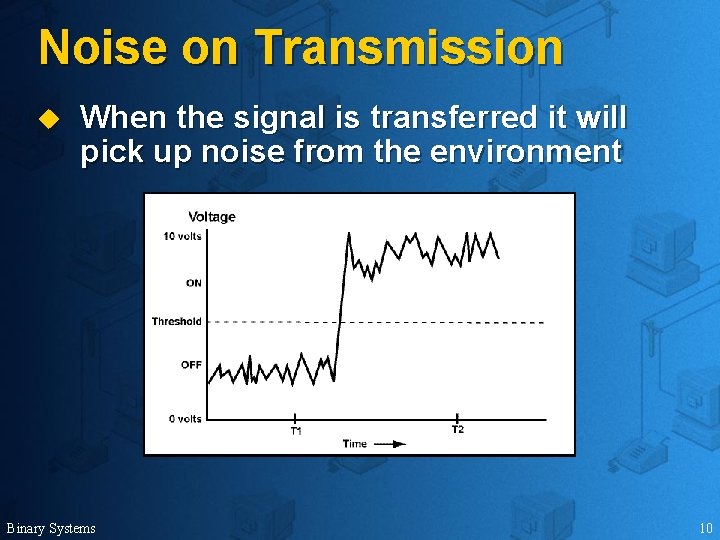
Noise on Transmission u When the signal is transferred it will pick up noise from the environment Binary Systems 10

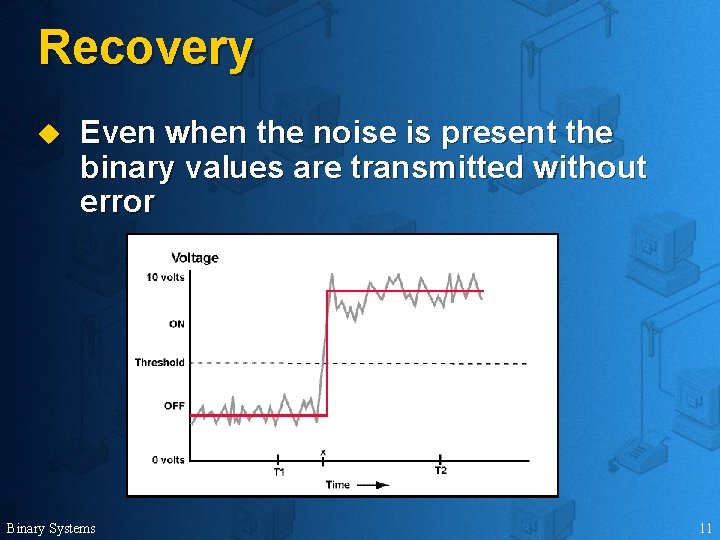
Recovery u Even when the noise is present the binary values are transmitted without error Binary Systems 11

Binary Numbers u A number in a base-r system x = xn-1 xn-2. . . x 1 x 0. x-1 x-2. . . X-(m-1) x-m Binary Systems 12

Radix Number System u Base – 2 (binary numbers) Ø u Base – 8 (octal numbers) Ø u 01 01234567 Base – 16 (hexadecimal numbers) Ø Binary Systems 0123456789 ABCDEF 13

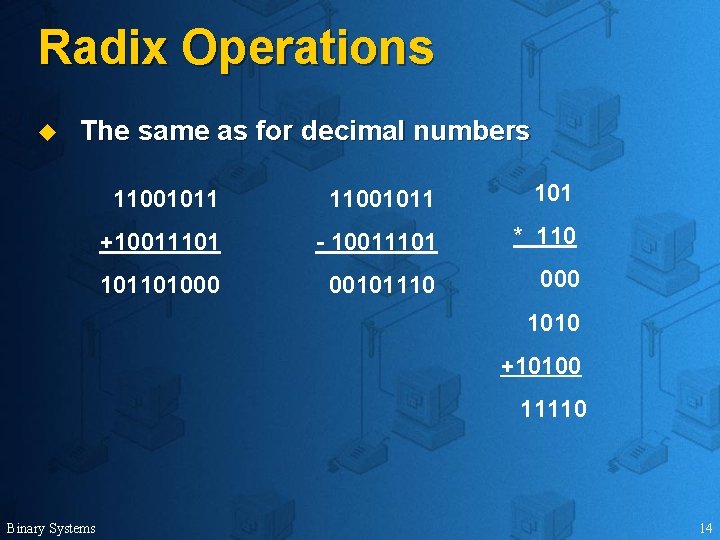
Radix Operations u The same as for decimal numbers 11001011 101 +10011101 - 10011101 * 110 101101000 00101110 000 1010 +10100 11110 Binary Systems 14

Conversion From one radix to another u From decimal to binary Binary Systems 15

Conversion From one radix to another u From decimal to base-r Ø Ø Separate the number into an integer part and a fraction part For the integer part ü Divide the number and all successive quotients by r ü Accumulate the remainders 165 Binary Systems 23 4 3 2 0 3 0. 6875 x 2 = 1 + 0. 3750 x 2 = 0 + 0. 7500 x 2 = 1 + 0. 5000 x 2 = 1 + 0. 0000 16

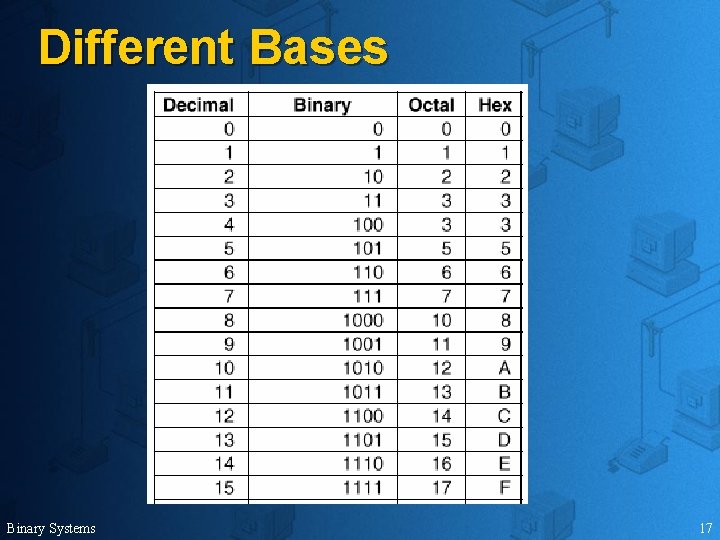
Different Bases Binary Systems 17

Conversion From one radix to another u From binary to octal Ø Ø Divide into groups of 3 bits Example ü u 11001101001000. 1011011 = 31510. 554 From octal to binary Ø Ø Replace each octal digit with three bits Example ü Binary Systems 75643. 5704 = 11110100011. 101111000100 18

Conversion From one radix to another u From binary to hexadecimal Ø Ø Divide into groups of 4 bits Example ü u 11001101001000. 1011011 = 3348. B 6 From hexadecimal to binary Ø Ø Replace each digit with four bits Example ü Binary Systems 7 BA 3. BC 4 = 11110100011. 101111000100 19

Complements u u They are used to simplify the subtraction operation Two types (for each base-r system) Ø Ø Diminishing radix complement (r-1 complement) Radix complement (r complement) For n-digit number N r-1 complement r complement Binary Systems 20

9’s and 10’s Complements u 9’s complement of 674653 Ø u 9’s complement of 023421 Ø u 999999 -023421 = 976578 10’s complement of 674653 Ø u 999999 -674653 = 325346+1 = 325347 10’s complement of 023421 Ø Binary Systems 976578+1=976579 21

1’s and 2’s Complements u 1’s complement of 10111001 Ø Ø u 1’s complement of 10100010 Ø u 01011101 2’s complement of 10111001 Ø Ø u 1111 – 10111001 = 01000110 Simply replace 1’s and 0’s 01000110 + 1 = 01000111 Add 1 to 1’s complement 2’s complement of 10100010 Ø Binary Systems 01011101 + 1 = 01011110 22

Subtraction with Complements of Unsigned u M–N Ø Add M to r’s complement of N ü Ø Ø If M > N, Sum will have an end carry rn , discard it If M<N, Sum will not have an end carry and ü ü Binary Systems Sum = M+(rn – N) = M – N+ rn Sum = rn – (N – M) (r’s complement of N – M) So M – N = – (r’s complement of Sum) 23

Subtraction with Complements of Unsigned u 65438 - 5623 65438 10’s complement of 05623 +94377 159815 Discard end carry 105 Answer Binary Systems -100000 59815 24

Subtraction with Complements of Unsigned u 5623 - 65438 05623 10’s complement of 65438 +34562 40185 There is no end carry => -(10’s complement of 40185) -59815 Binary Systems 25

Subtraction with Complements of Unsigned u 10110010 - 10011111 10110010 2’s complement of 10011111 Discard end carry 2^8 Answer Binary Systems +01100001 100010011 -1000010011 26

Subtraction with Complements of Unsigned u 10011111 -10110010 10011111 2’s complement of 10110010 +010011101101 There is no end carry => -(2’s complement of 11101101) Answer = -00010011 Binary Systems 27

Signed Binary Numbers u u Unsigned representation can be used for positive integers How about negative integers? Ø Ø Binary Systems Everything must be represented in binary numbers Computers cannot use – or + signs 28

Negative Binary Numbers u Three different systems have been used Ø Ø Ø Signed magnitude One’s complement Two’s complement NOTE: For negative numbers the sign bit is always 1, and for positive numbers it is 0 in these three systems Binary Systems 29

Signed Magnitude u u The leftmost bit is the sign bit (0 is + and 1 is - ) and the remaining bits hold the absolute magnitude of the number Examples ü ü -47 = 1 0 1 1 47 = 0 0 1 1 1 1 For 8 bits, we can represent the signed integers – 128 to +127 How about for N bits? Binary Systems 30

One’s complement u u Replace each 1 by 0 and each 0 by 1 Example (-6) Ø Ø Binary Systems First represent 6 in binary format (00000110) Then replace (11111001) 31

Two’s complement u u u Find one’s complement Add 1 Example (-6) Ø Ø Ø Binary Systems First represent 6 in binary format (00000110) One’s complement (11111001) Two’s complement (11111010) 32

Arithmetic Addition u Usually represented by 2’s complement Discard +5 00000101 -5 11111011 +11 00001011 +16 00010000 +6 100000110 +5 00000101 -5 11111011 -11 11110101 -6 11111010 -16 111110000 Binary Systems Discard 33

Registers u u They can hold a groups of binary data Data can be transferred from one register to another Binary Systems 34

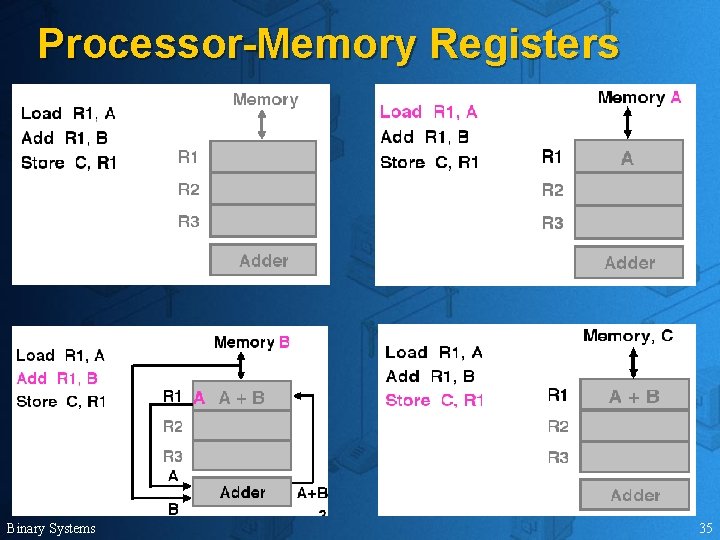
Processor-Memory Registers Binary Systems 35

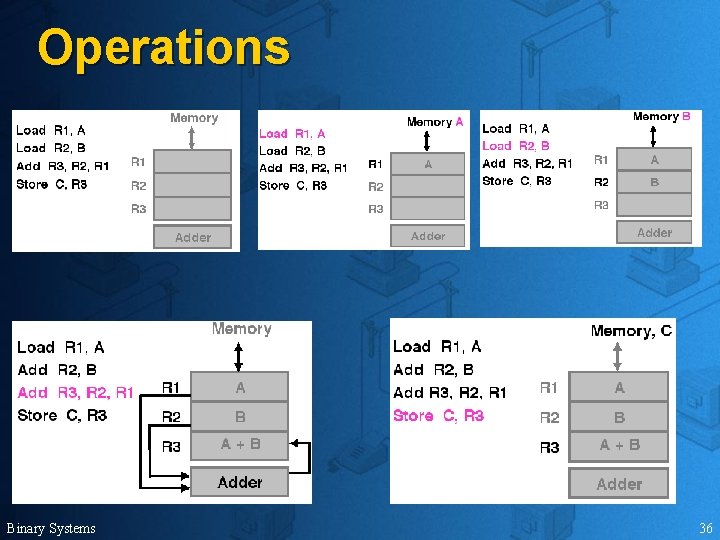
Operations Binary Systems 36

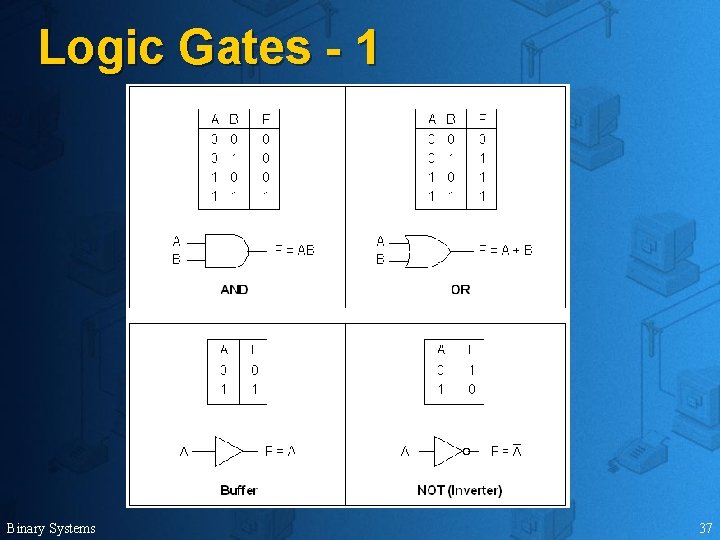
Logic Gates - 1 Binary Systems 37

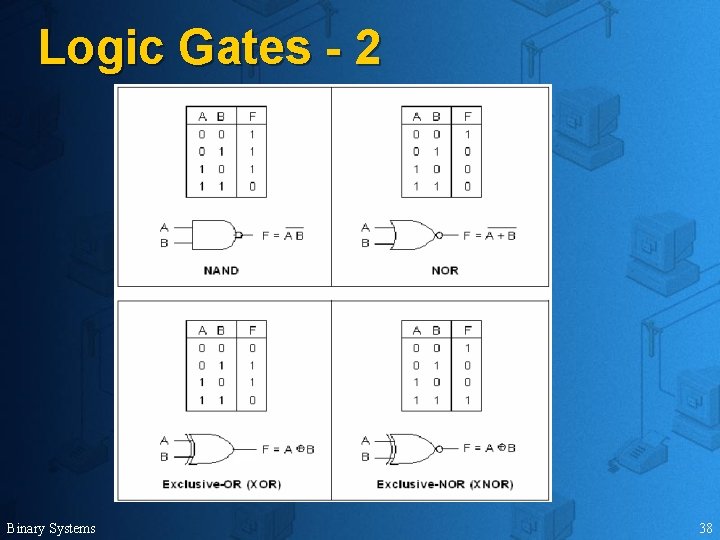
Logic Gates - 2 Binary Systems 38

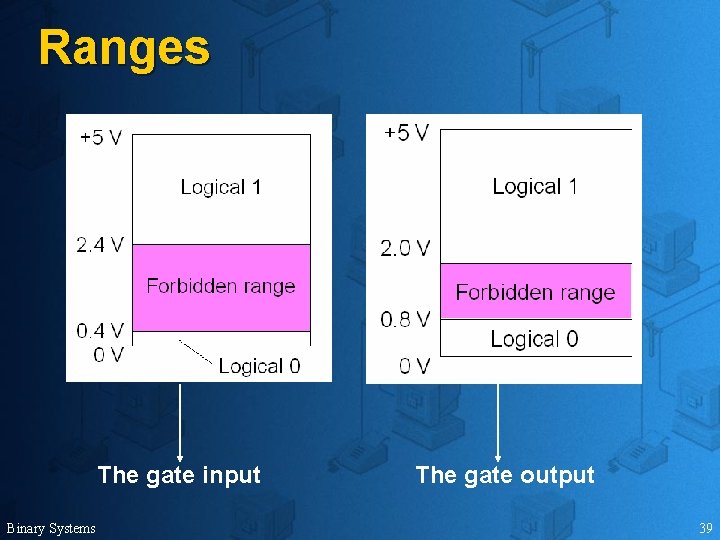
Ranges The gate input Binary Systems The gate output 39

Study Problems u Course Book Chapter – 1 Problems Ø Ø Ø Ø Binary Systems 1– 2 1– 7 1– 8 1 – 20 1 – 34 1 – 35 1 – 36 40

Sneak Preview u Next time Ø ASSIGNMENT ü Ø Will be given QUIZ……. ü Expect a question from each one of the following Ø Ø Binary Systems Convert decimal to any base Convert between binary, octal, and hexadecimal Binary add, subtract, and multiply Negative numbers 41

Questions Binary Systems 42