Digital Lesson Solving Trigonometric Equations sin x is

Digital Lesson Solving Trigonometric Equations

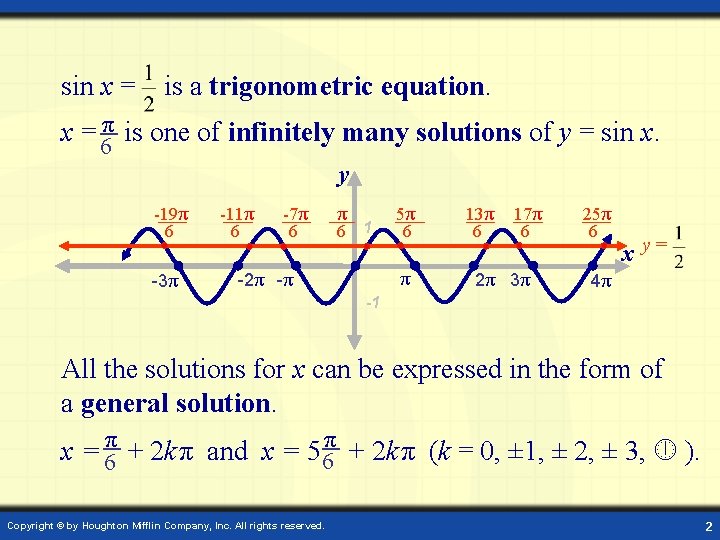
sin x = is a trigonometric equation. x = 6π is one of infinitely many solutions of y = sin x. y -19π 6 -3π -11π 6 -7π 6 1 5π 6 π -2π -π 13π 6 17π 6 2π 3π 25π 6 x y= 4π -1 All the solutions for x can be expressed in the form of a general solution. x = 6π + 2 k π and x = 56π + 2 k π (k = 0, ± 1, ± 2, ± 3, ). Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 2

Find the general solution for the equation sec = 2. From cos = 1 , it follows that cos =. sec All values of for which cos = are solutions of the equation. Two solutions are = ± π. 3 All angles that are coterminal with ± π are also solutions and 3 can be expressed by adding integer multiples of 2π. cos( π3 + 2 kπ) = P y 1 x Q cos( -π3 + 2 kπ) = The general solution can be written as = ± π + 2 kπ. 3 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 3

Example: Solve tan x = 1. The graph of y = 1 intersects the graph of y = tan x infinitely y many times. - π – 2π 4 -π–π 4 π + π π + 2π 4 π + 3π 4 4 y=1 -π π 2π 3π x y = tan(x) x = -3π x = -π 2 2 x = π x = 3π x = 5π 2 2 2 Points of intersection are at x = π and every multiple of π added or 4 π subtracted from 4. General solution: x = π + kπ for k any integer. 4 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 4

Example: Solve the equation 3 sin x + 2 =0 2 y = sin x 3 sin x + 2 sin x + = sin x for π ≤ x ≤ π. =0 Collect like terms. sin x = 1 -π 1 4 x y=- x = 4π is the only solution in the interval 2π ≤ x ≤ 2π. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 5

Example: To find all solutions of cos 4(2 x) = 9. 16 Take the fourth root of both sides to obtain: cos(2 x)= ± y From the unit circle, the solutions for 2 are 2 = ± 6π + kπ, k any integer. π π 1 π 6 -π x 6 x=- x= Answer: = ± π + k ( π ), for k any integer. 12 2 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 6

Find all solutions of the trigonometric equation: tan 2 + tan = 0 tan (tan +1) = 0 Original equation Factor. Therefore, tan = 0 or tan = -1. The solutions for tan = 0 are the values = kπ, for k any integer. The solutions for tan = 1 are = - 4π + kπ, for k any integer. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 7

The trigonometric equation 2 sin 2 + 3 sin + 1 = 0 is quadratic in form. 2 sin 2 + 3 sin + 1 = 0 implies that (2 sin + 1)(sin + 1) = 0. Therefore, 2 sin + 1 = 0 or sin + 1 = 0. It follows that sin = - 1 or sin = -1. 2 Solutions: = - π + 2 kπ and = 7π + 2 kπ, from sin = - 1 6 6 2 = -π + 2 kπ, from sin = -1 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 8

Example: Solve 8 sin = 3 cos 2 with in the interval [0, 2π]. Rewrite the equation in terms of only one trigonometric function. 8 sin = 3(1 sin 2 ) Use the Pythagorean Identity. 3 sin 2 + 8 sin 3 = 0. A “quadratic” equation with sin x as the variable (3 sin 1)(sin + 3) = 0 Factor. Therefore, 3 sin 1 = 0 or sin + 3 = 0 Solutions: sin = 1 or sin = -3 3 = sin 1( 1 ) = 0. 3398 and = π sin 1( 1 ) = 2. 8107. 3 3 s Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 9

Solve: 5 cos 2 + cos – 3 = 0 for 0 ≤ ≤ π. The equation is quadratic. Let y = cos and solve 5 y 2 + y 3 = 0. y = (-1 ± 10 ) = 0. 6810249 or -0. 8810249 Therefore, cos = 0. 6810249 or – 0. 8810249. Use the calculator to find values of in 0 ≤ ≤ π. This is the range of the inverse cosine function. The solutions are: = cos 1(0. 6810249 ) = 0. 8216349 and = cos 1( 0. 8810249) = 2. 6488206 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 10

Example: Find the intersection points of the graphs of y y = sin and y = cos . The two solutions for between 0 and 2π are π and 5π. 4 4 5 -π 4 π + kπ 4 1 -π 4 π + kπ 4 x 1 The graphs of y = sin and y = cos intersect at points where sin = cos . This is true only for 45 -45 -90 triangles. The general solution is = 4π + kπ, for k any integer. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 11