Digital Lesson Shifting Graphs The graphs of many

Digital Lesson Shifting Graphs

The graphs of many functions are transformations of the graphs of very basic functions. Example: The graph of y = x 2 + 3 is the graph of y = x 2 shifted upward three units. This is a vertical shift. The graph of y = -x 2 is the reflection of the graph of y = x 2 in the x-axis. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. y y = x 2 + 3 8 y = x 2 4 x 4 -4 -4 y = -x 2 -8 2

Vertical Shifts If c is a positive real number, the graph of f(x) + c is the graph of y = f(x) shifted upward c units. If c is a positive real number, the graph of f(x) – c is the graph of y = f(x) shifted downward c units. y f(x) + c +c -c f(x) – c x Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 3

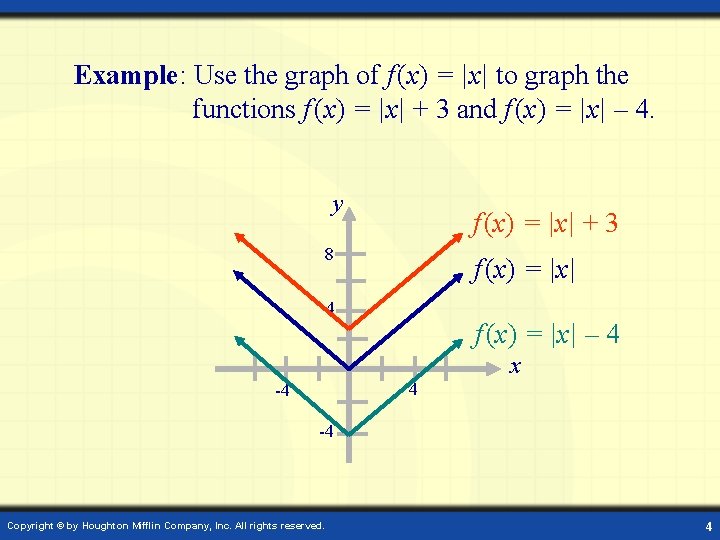
Example: Use the graph of f (x) = |x| to graph the functions f (x) = |x| + 3 and f (x) = |x| – 4. y f (x) = |x| + 3 8 f (x) = |x| 4 f (x) = |x| – 4 x 4 -4 -4 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 4

Horizontal Shifts If c is a positive real number, then the graph of f (x – c) is the graph of y = f (x) shifted to the right c units. y If c is a positive real number, then the graph of f (x + c) is the graph of y = f (x) shifted to the left c units. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. -c +c y = f (x + c) y = f (x) x y = f (x – c) 5

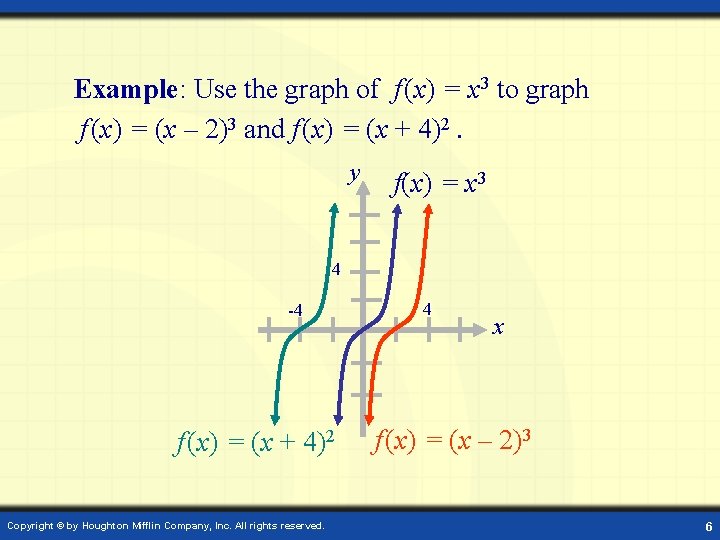
Example: Use the graph of f (x) = x 3 to graph f (x) = (x – 2)3 and f (x) = (x + 4)2. y f(x) = x 3 4 -4 f (x) = (x + 4)2 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 4 x f (x) = (x – 2)3 6

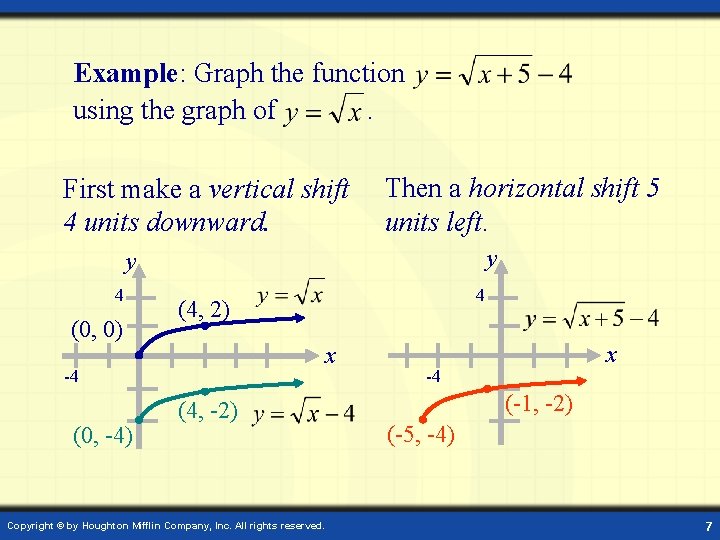
Example: Graph the function using the graph of. First make a vertical shift 4 units downward. Then a horizontal shift 5 units left. y y 4 (0, 0) (4, 2) x -4 (0, -4) 4 (4, -2) Copyright © by Houghton Mifflin Company, Inc. All rights reserved. x -4 (-1, -2) (-5, -4) 7

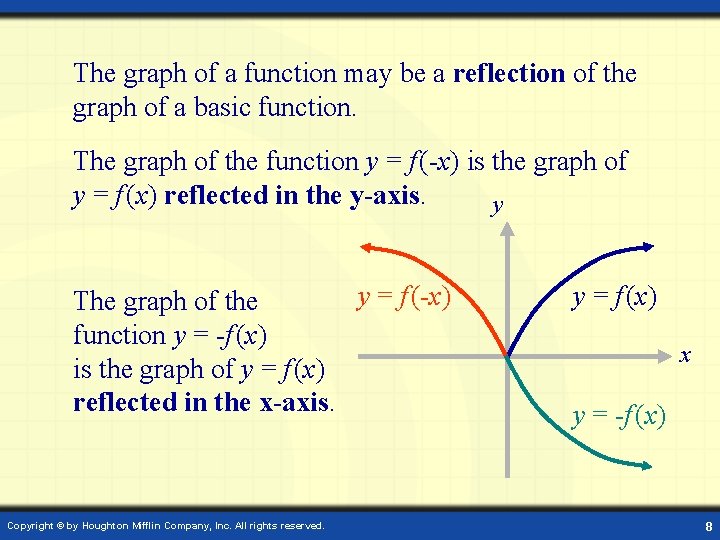
The graph of a function may be a reflection of the graph of a basic function. The graph of the function y = f (-x) is the graph of y = f (x) reflected in the y-axis. y y = f (-x) The graph of the function y = -f (x) is the graph of y = f (x) reflected in the x-axis. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. y = f (x) x y = -f (x) 8

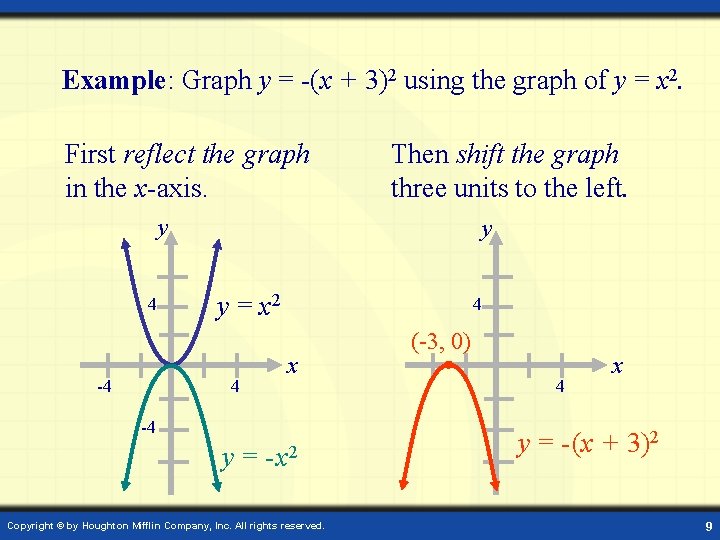
Example: Graph y = -(x + 3)2 using the graph of y = x 2. First reflect the graph in the x-axis. Then shift the graph three units to the left. y 4 y y = x 2 4 -4 4 x -4 y = - x 2 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. (-3, 0) 4 x y = - (x + 3)2 9

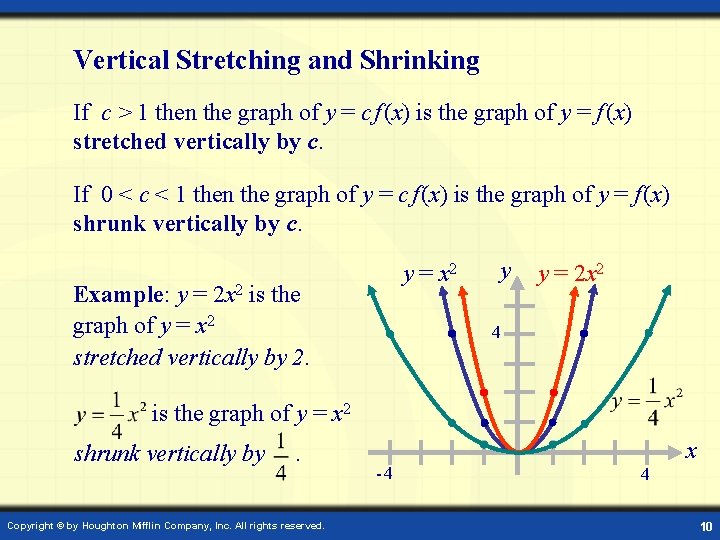
Vertical Stretching and Shrinking If c > 1 then the graph of y = c f (x) is the graph of y = f (x) stretched vertically by c. If 0 < c < 1 then the graph of y = c f (x) is the graph of y = f (x) shrunk vertically by c. y = x 2 Example: y = 2 x 2 is the graph of y = x 2 stretched vertically by 2. y y = 2 x 2 4 is the graph of y = x 2 shrunk vertically by . Copyright © by Houghton Mifflin Company, Inc. All rights reserved. -4 x 4 10

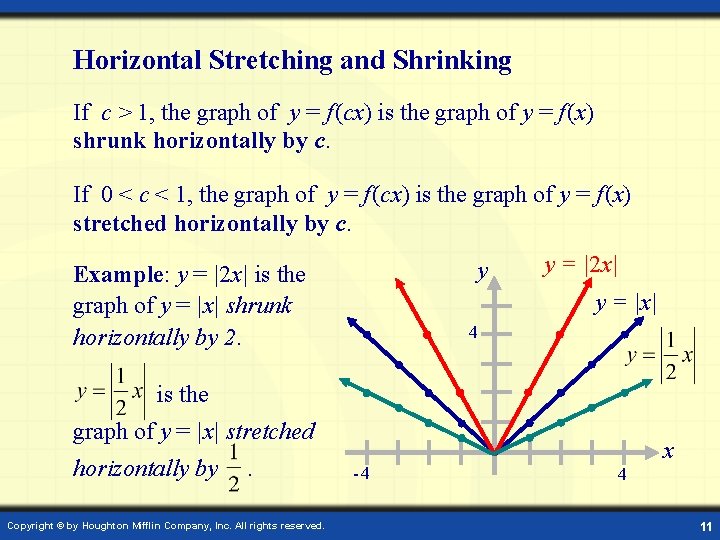
Horizontal Stretching and Shrinking If c > 1, the graph of y = f (cx) is the graph of y = f (x) shrunk horizontally by c. If 0 < c < 1, the graph of y = f (cx) is the graph of y = f (x) stretched horizontally by c. y Example: y = |2 x| is the graph of y = |x| shrunk horizontally by 2. y = |2 x| y = |x| 4 is the graph of y = |x| stretched horizontally by . Copyright © by Houghton Mifflin Company, Inc. All rights reserved. -4 x 4 11

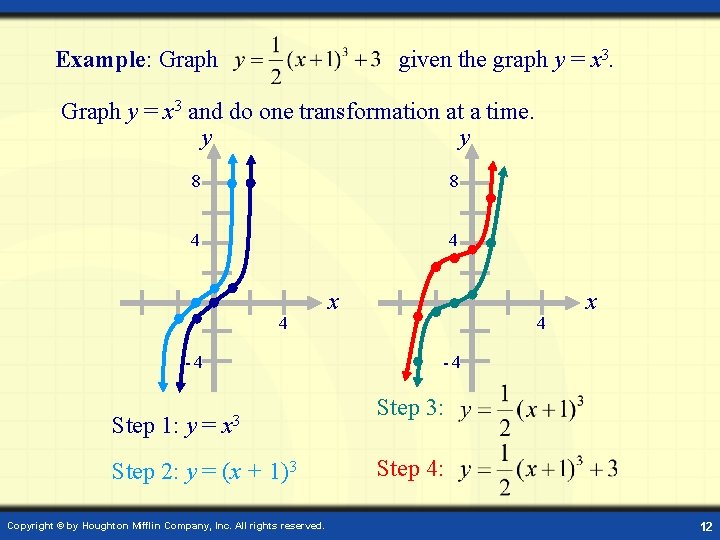
Example: Graph given the graph y = x 3. Graph y = x 3 and do one transformation at a time. y y 8 8 4 4 x -4 -4 Step 1: y = x x 3 Step 2: y = (x + 1)3 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. Step 3: Step 4: 12