Digital Lesson Logarithmic Functions For x 0 and

Digital Lesson Logarithmic Functions

For x 0 and 0 a 1, y = loga x if and only if x = a y. The function given by f (x) = loga x is called the logarithmic function with base a. Every logarithmic equation has an equivalent exponential form: y = loga x is equivalent to x = a y A logarithm is an exponent! A logarithmic function is the inverse function of an exponential function. Exponential function: y = ax Logarithmic function: y = logax is equivalent to x = ay Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 2

Examples: Write the equivalent exponential equation and solve for y. Logarithmic Equation Equivalent Exponential Equation Solution 16 = 2 y 16 = 24 y = 4 y = log 216 y = log 2( ) y = log 416 y = log 51 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. = 2 y = 2 -1 y = – 1 16 = 4 y 16 = 42 y = 2 1=5 y 1 = 50 y = 0 3

The base 10 logarithm function f (x) = log 10 x is called the common logarithm function. The LOG key on a calculator is used to obtain common logarithms. Examples: Calculate the values using a calculator. Function Value Keystrokes Display log 10 100 LOG 100 ENTER 2 log 10( LOG ( 2 – 0. 3979400 log 10 5 log 10 – 4 ) 5 ) ENTER LOG 5 ENTER LOG – 4 ENTER 0. 6989700 ERROR no power of 10 gives a negative number Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 4

Properties of Logarithms 1. loga 1 = 0 since a 0 = 1. 2. loga a = 1 since a 1 = a. 3. loga ax = x and alogax = x inverse property 4. If loga x = loga y, then x = y. one-to-one property Examples: Solve for x: log 6 6 = x log 6 6 = 1 property 2 x = 1 Simplify: log 3 35 = 5 property 3 Simplify: 7 log 79 = 9 property 3 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 5

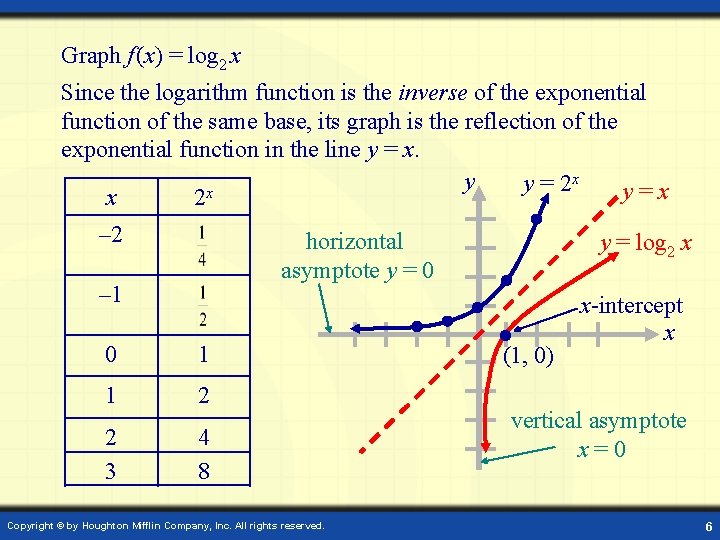
Graph f (x) = log 2 x Since the logarithm function is the inverse of the exponential function of the same base, its graph is the reflection of the exponential function in the line y = x. x y y = 2 y=x x 2 x – 2 horizontal asymptote y = 0 – 1 0 1 1 2 2 3 4 8 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. y = log 2 x (1, 0) x-intercept x vertical asymptote x=0 6

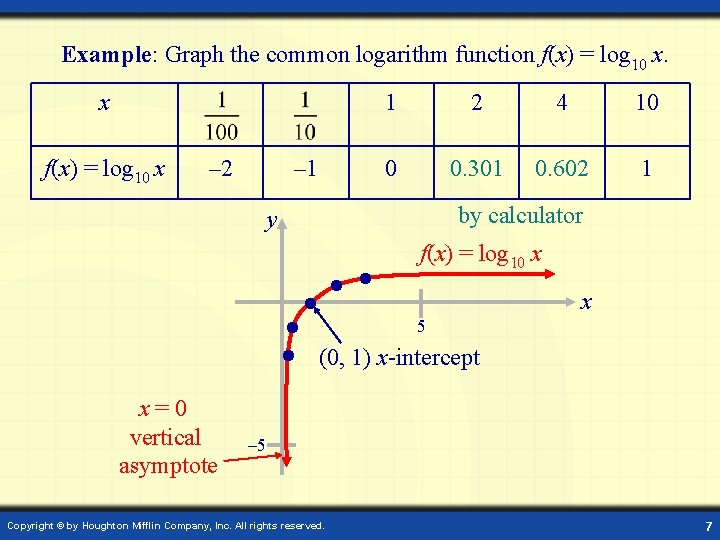
Example: Graph the common logarithm function f(x) = log 10 x. x f(x) = log 10 x – 2 – 1 1 2 4 10 0 0. 301 0. 602 1 by calculator y f(x) = log 10 x x 5 (0, 1) x-intercept x=0 vertical asymptote – 5 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 7

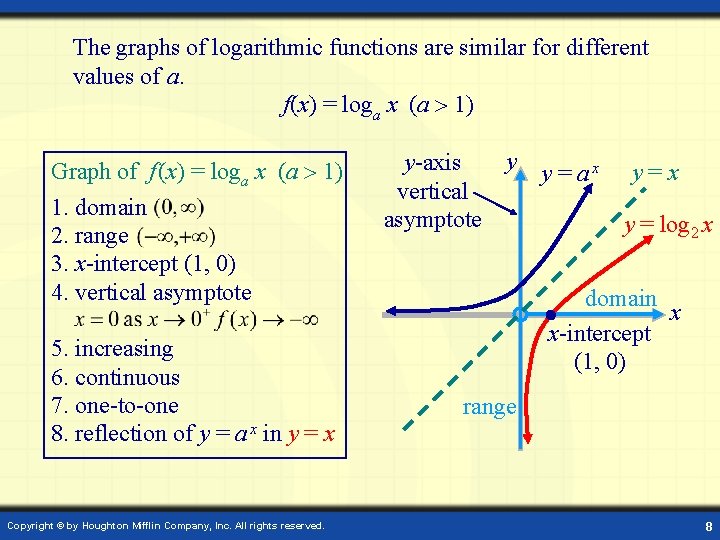
The graphs of logarithmic functions are similar for different values of a. f(x) = loga x (a 1) Graph of f (x) = loga x (a 1) 1. domain 2. range 3. x-intercept (1, 0) 4. vertical asymptote 5. increasing 6. continuous 7. one-to-one 8. reflection of y = a x in y = x Copyright © by Houghton Mifflin Company, Inc. All rights reserved. y-axis vertical asymptote y y = ax y=x y = log 2 x domain x x-intercept (1, 0) range 8

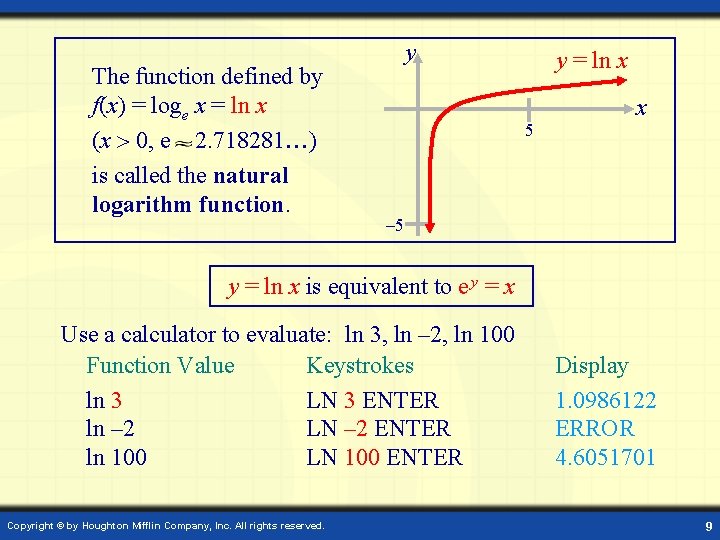
The function defined by f(x) = loge x = ln x (x 0, e 2. 718281 ) is called the natural logarithm function. y y = ln x 5 x – 5 y = ln x is equivalent to e y = x Use a calculator to evaluate: ln 3, ln – 2, ln 100 Function Value Keystrokes ln 3 LN 3 ENTER ln – 2 LN – 2 ENTER ln 100 LN 100 ENTER Copyright © by Houghton Mifflin Company, Inc. All rights reserved. Display 1. 0986122 ERROR 4. 6051701 9

Properties of Natural Logarithms 1. ln 1 = 0 since e 0 = 1. 2. ln e = 1 since e 1 = e. 3. ln ex = x and eln x = x inverse property 4. If ln x = ln y, then x = y. one-to-one property Examples: Simplify each expression. inverse property 2 property 1 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 10

Example: The formula (t in years) is used to estimate the age of organic material. The ratio of carbon 14 to carbon 12 in a piece of charcoal found at an archaeological dig is . How old is it? original equation multiply both sides by 1012 take the natural log of both sides inverse property To the nearest thousand years the charcoal is 57, 000 years old. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 11