Digital Lesson Conic Sections Conic sections are plane

Digital Lesson Conic Sections

Conic sections are plane figures formed by the intersection of a double-napped cone and a plane. Parabola Ellipse Hyperbola The conic sections may be defined as sets of points in the plane that satisfy certain geometrical properties. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 2

A parabola is the set of all points in the plane equidistant from a fixed line and a fixed point not on the line. The fixed line is the directrix. The fixed point is the focus. The axis is the line passing through the focus and perpendicular to the directrix. The vertex is the midpoint of the line segment along the axis joining the directrix to the focus. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. axis parabola focus directrix vertex 3

The standard form for the equation of a parabola with vertex at the origin and a vertical axis is: x 2 = 4 py where p 0 vertical axis: x = 0 directrix: y = –p, focus: (0, p) y (0, p) p x 2 = 4 py x (0, 0) y = –p Note: p is the directed distance from the vertex to the focus. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 4

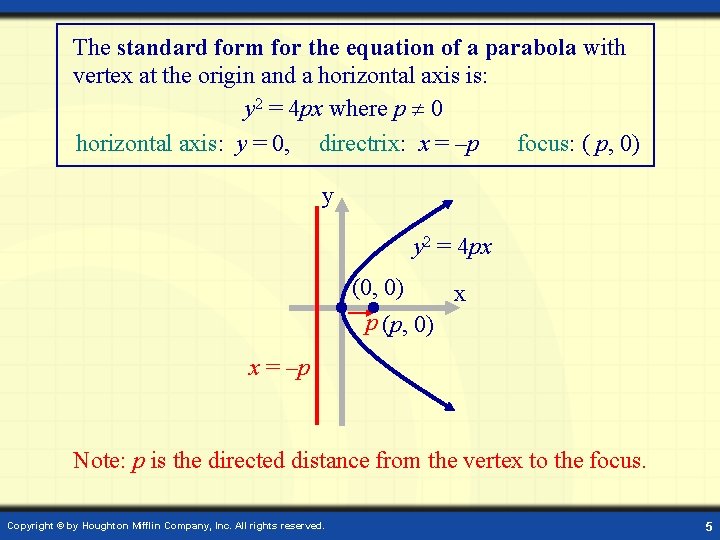
The standard form for the equation of a parabola with vertex at the origin and a horizontal axis is: y 2 = 4 px where p 0 horizontal axis: y = 0, directrix: x = –p focus: ( p, 0) y y 2 = 4 px (0, 0) x p (p, 0) x = –p Note: p is the directed distance from the vertex to the focus. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 5

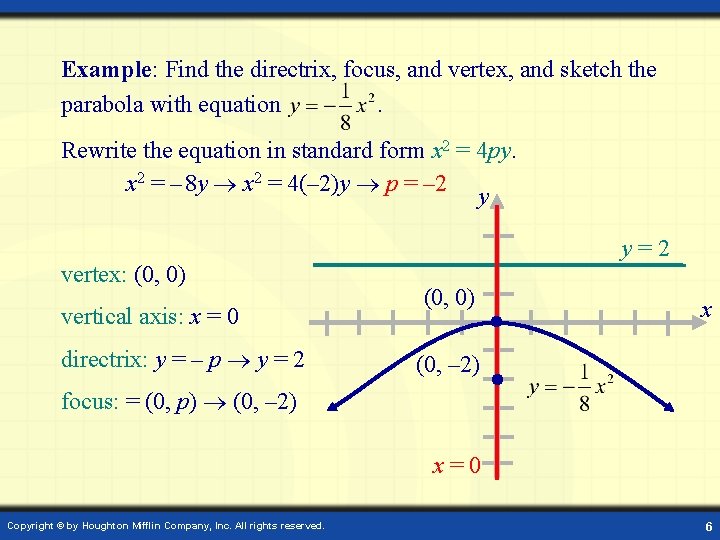
Example: Find the directrix, focus, and vertex, and sketch the parabola with equation. Rewrite the equation in standard form x 2 = 4 py. x 2 = – 8 y x 2 = 4(– 2)y p = – 2 y vertex: (0, 0) vertical axis: x = 0 directrix: y = – p y = 2 y=2 (0, 0) x (0, – 2) focus: = (0, p) (0, – 2) x=0 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 6

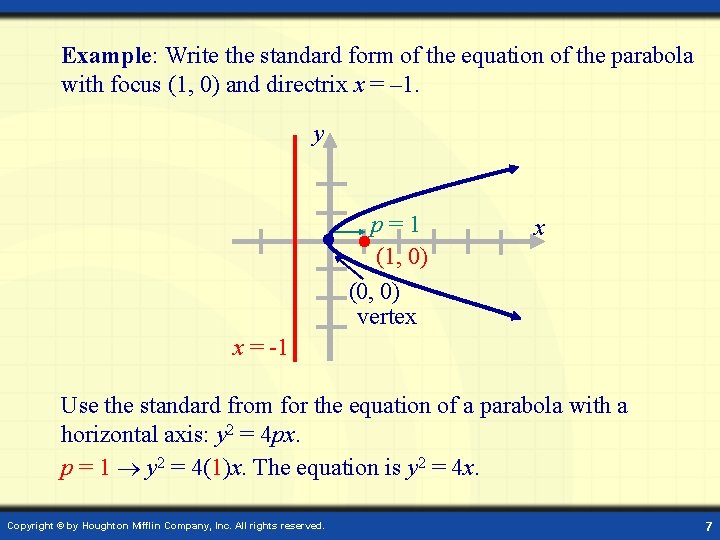
Example: Write the standard form of the equation of the parabola with focus (1, 0) and directrix x = – 1. y p=1 (1, 0) (0, 0) vertex x x = -1 Use the standard from for the equation of a parabola with a horizontal axis: y 2 = 4 px. p = 1 y 2 = 4(1)x. The equation is y 2 = 4 x. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 7

An ellipse is the set of all points in the plane for which the sum of the distances to two fixed points (called foci) is a positive constant. The major axis is the line segment passing through the foci with endpoints (called vertices) on the ellipse. The midpoint of the major axis is the center of the ellipse. vertex The minor axis is the line segment perpendicular to the major axis passing through the center of the ellipse with endpoints on the ellipse. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. Ellipse focus d 1 center d 1 + d 2 = constant d 2 focus major axis vertex minor axis 8

The standard form for the equation of an ellipse with center at the origin and a major axis that is horizontal is: , with: vertices: (–a, 0), (a, 0) and foci: (–c, 0), (c, 0) where c 2 = a 2 – b 2 y a c (– a, 0) (–c, 0) (0, b) b x a (0, 0) (c, 0) (a, 0) (0, – b) Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 9

The standard form for the equation of an ellipse with center at the origin and a major axis that is vertical is: , with: vertices: (0, –a), (0, a) and foci: (0, –c), (0, c) where c 2 = a 2 – b 2 y a (– b, 0) b (0, a) (0, c) c (0, 0) x b (b, 0) a (0, -c) (0, – a) Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 10

Example: Sketch the ellipse with equation 25 x 2 + 16 y 2 = 400 and find the vertices and foci. y 1. Put the equation into standard form. divide by 400 (0, 5) (0, 3) 5 (4, 0) 3 x So, a = 5 and b = 4. (– 4, 0) 4 2. Since the denominator of the y 2 -term is larger, the major axis is vertical. (0, – 3) (0, – 5) 3. Vertices: (0, – 5), (0, 5) 4. The minor axis is horizontal and intersects the ellipse at (– 4, 0) and (4, 0). 5. Foci: c 2 = a 2 – b 2 (5)2 – (4)2 = 9 c = 3 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. foci: (0, – 3), (0, 3) 11

A hyperbola is the set of all points in the plane for which the difference from two fixed points (the foci) is a positive constant. The graph of the hyperbola has two branches. hyperbola transverse axis The line through the foci intersects the hyperbola at two points called vertices. focus The line segment joining the vertices is the transverse axis. Its midpoint is the center of the hyperbola. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. vertex d 1 vertex focus d 2 center d 2 – d 1 = constant 12

The standard form for the equation of a hyperbola with a horizontal transverse axis is: with: vertices: (– a, 0), (a, 0) and foci: (– c, 0), (c, 0) where b 2 = c 2 – a 2 vertex (– a, 0) asymptote y (0, b) vertex (a, 0) focus x (c, 0) asymptote focus (–c, 0) (0, –b) A hyperbola with a horizontal transverse axis has asymptotes with equations and. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 13

The standard form for the equation of a hyperbola with a vertical transverse axis is: with: vertices: (0, – a), (0, a) and foci: (0, – c), (0, c) where b 2 = c 2 – a 2 y asymptote focus (0, c) vertex (0, a) x (b, 0) asymptote (–b, 0) vertex (0, – a) focus (0, -c) A hyperbola with a vertical transverse axis has asymptotes with equations and Copyright © by Houghton Mifflin Company, Inc. All rights reserved. . 14

Example: Sketch the hyperbola with equation x 2 – 9 y 2 = 9 and find the vertices, foci, and asymptotes. 1. To write the equation in standard form, divide by 9. 2. Because the x 2 -term is positive, the transverse axis is horizontal. y 3. Vertices: (0, – 3), (0, 3) (0, 1) 4. Asymptotes: x 5. a = 3 and b = 1 foci: Copyright © by Houghton Mifflin Company, Inc. All rights reserved. (-3, 0) (0, -1) (3, 0) 15