Digital Integrated Circuits A Design Perspective Jan M

Digital Integrated Circuits A Design Perspective Jan M. Rabaey Anantha Chandrakasan Borivoje Nikolic Arithmetic Circuits January, 2003 © EE 141 Digital Integrated Circuits 2 nd 1 Arithmetic Circuits

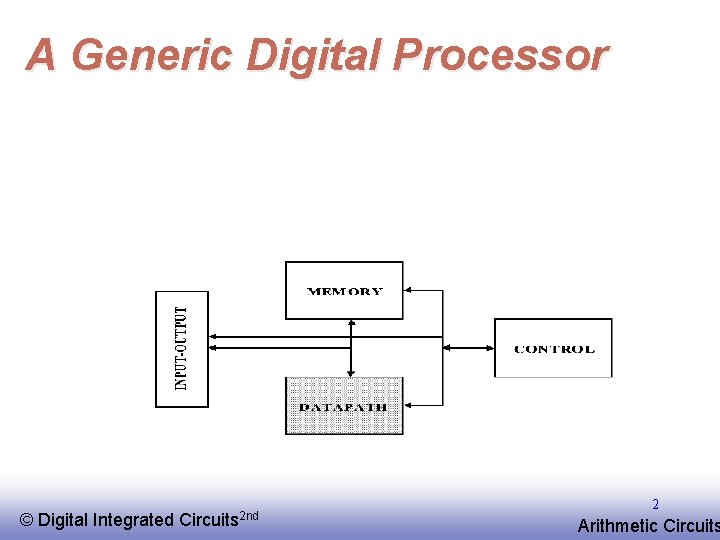
A Generic Digital Processor © EE 141 Digital Integrated Circuits 2 nd 2 Arithmetic Circuits

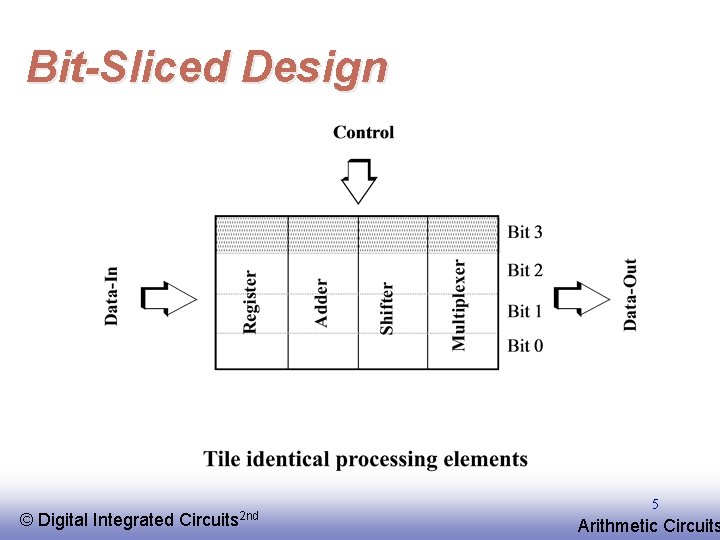
Building Blocks for Digital Architectures Arithmetic unit - Bit-sliced datapath (adder, multiplier, shifter, comparator, etc. ) Memory - RAM, ROM, Buffers, Shift registers Control - Finite state machine (PLA, random logic. ) - Counters Interconnect - Switches - Arbiters - Bus © EE 141 Digital Integrated Circuits 2 nd 3 Arithmetic Circuits

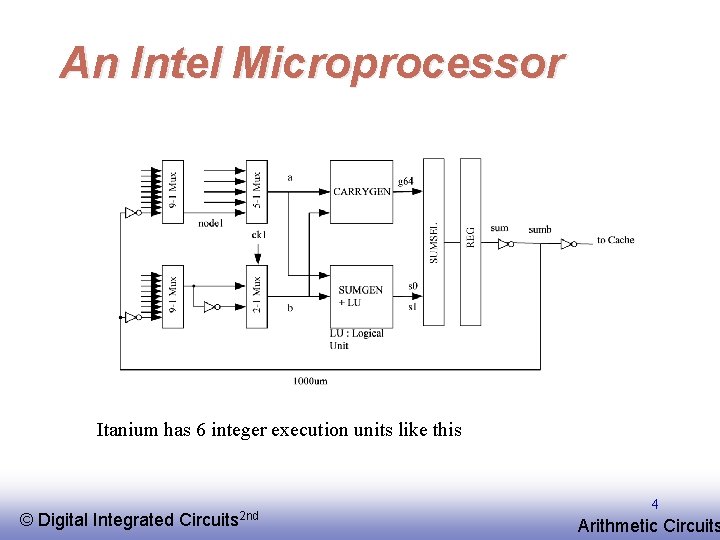
An Intel Microprocessor Itanium has 6 integer execution units like this © EE 141 Digital Integrated Circuits 2 nd 4 Arithmetic Circuits

Bit-Sliced Design © EE 141 Digital Integrated Circuits 2 nd 5 Arithmetic Circuits

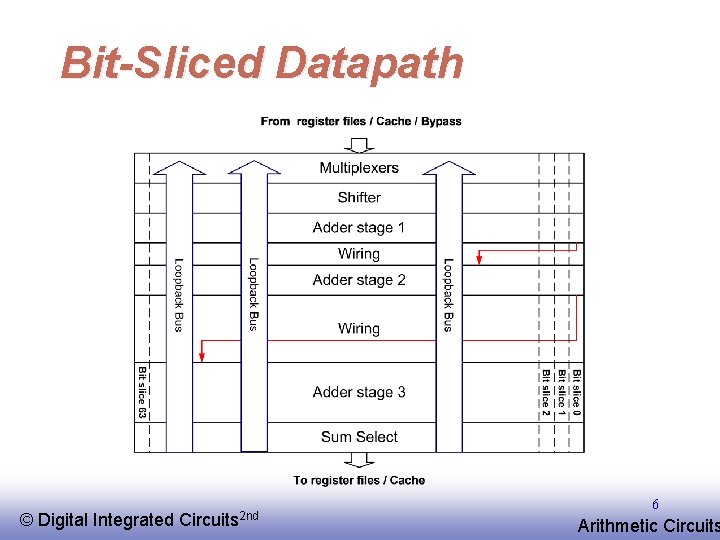
Bit-Sliced Datapath © EE 141 Digital Integrated Circuits 2 nd 6 Arithmetic Circuits

Itanium Integer Datapath Fetzer, Orton, ISSCC’ 022 nd © EE 141 Digital Integrated Circuits 7 Arithmetic Circuits

Adders © EE 141 Digital Integrated Circuits 2 nd 8 Arithmetic Circuits

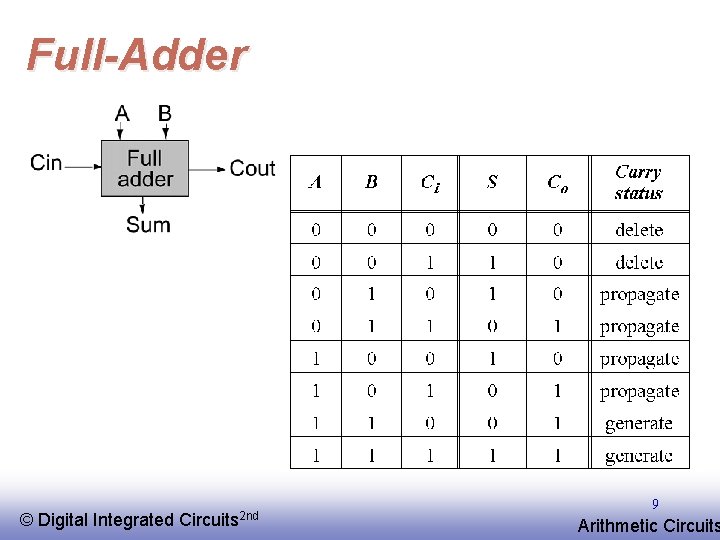
Full-Adder © EE 141 Digital Integrated Circuits 2 nd 9 Arithmetic Circuits

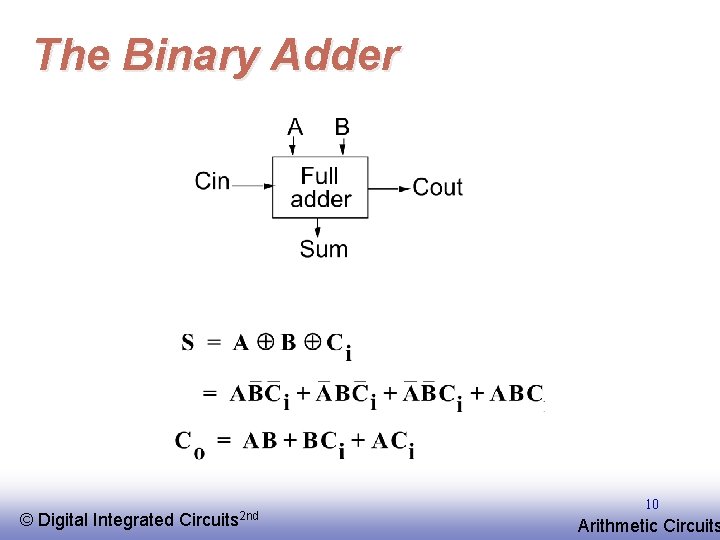
The Binary Adder © EE 141 Digital Integrated Circuits 2 nd 10 Arithmetic Circuits

Express Sum and Carry as a function of P, G, D Define 3 new variable which ONLY depend on A, B Generate (G) = AB Propagate (P) = A Å B Delete = A B Can also derive expressions for S and Co based on D and P Note that we will be sometimes using an alternate definition for Propagate (P) = A + B © EE 141 Digital Integrated Circuits 2 nd 11 Arithmetic Circuits

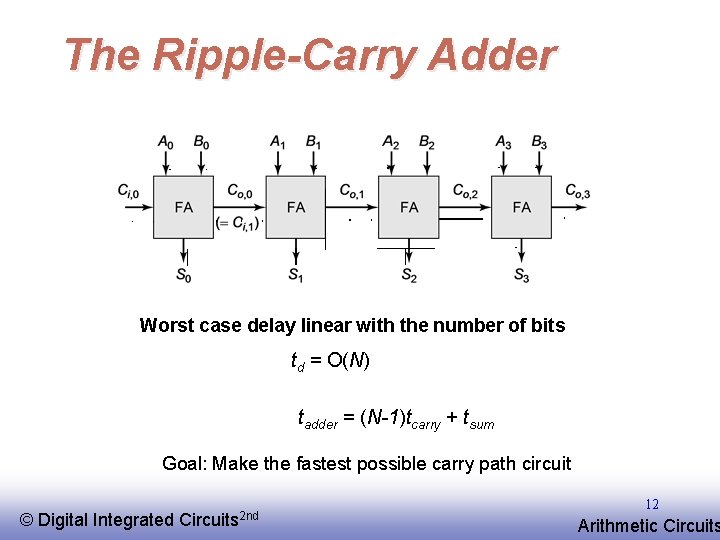
The Ripple-Carry Adder Worst case delay linear with the number of bits td = O(N) tadder = (N-1)tcarry + tsum Goal: Make the fastest possible carry path circuit © EE 141 Digital Integrated Circuits 2 nd 12 Arithmetic Circuits

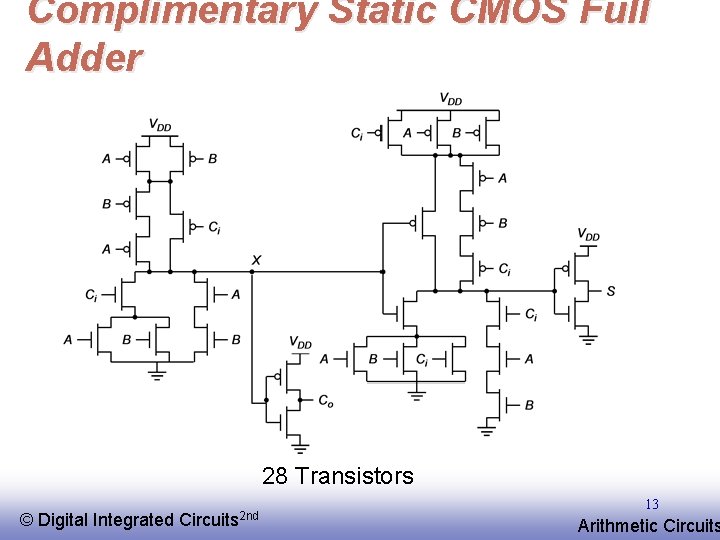
Complimentary Static CMOS Full Adder 28 Transistors © EE 141 Digital Integrated Circuits 2 nd 13 Arithmetic Circuits

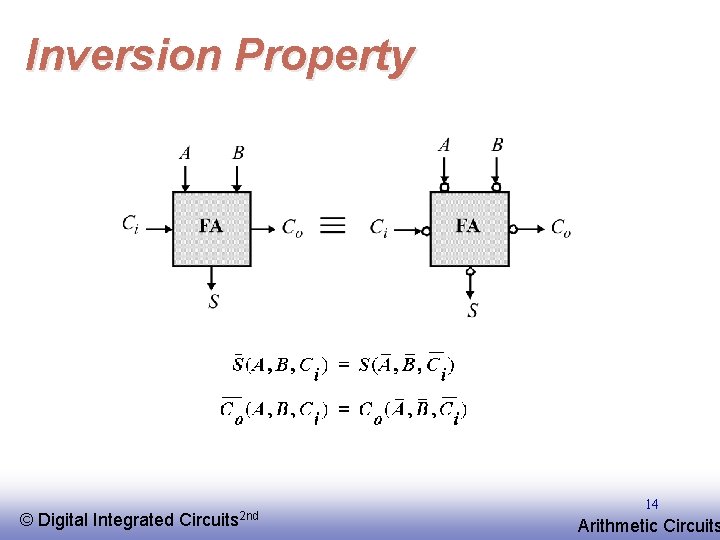
Inversion Property © EE 141 Digital Integrated Circuits 2 nd 14 Arithmetic Circuits

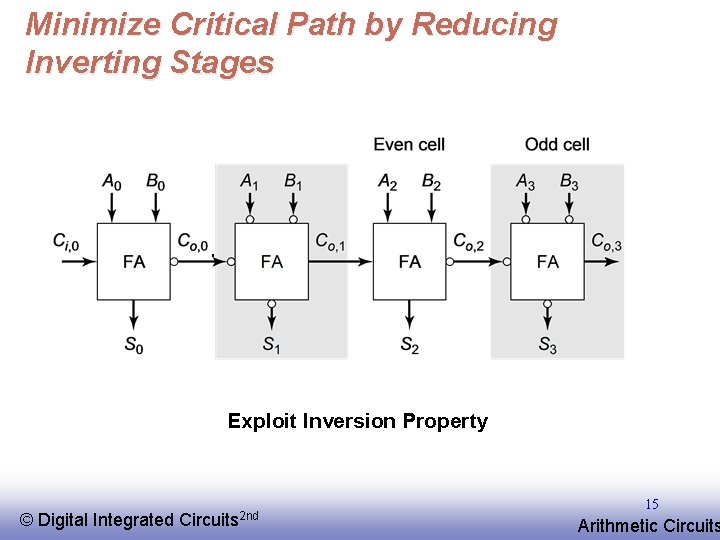
Minimize Critical Path by Reducing Inverting Stages Exploit Inversion Property © EE 141 Digital Integrated Circuits 2 nd 15 Arithmetic Circuits

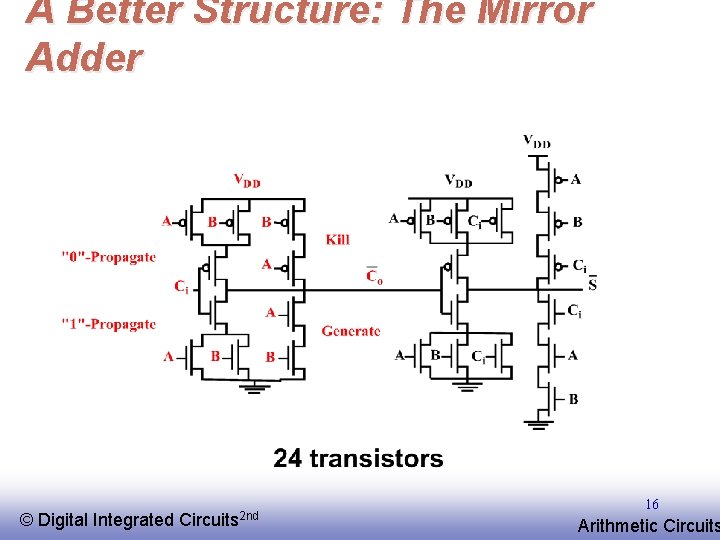
A Better Structure: The Mirror Adder © EE 141 Digital Integrated Circuits 2 nd 16 Arithmetic Circuits

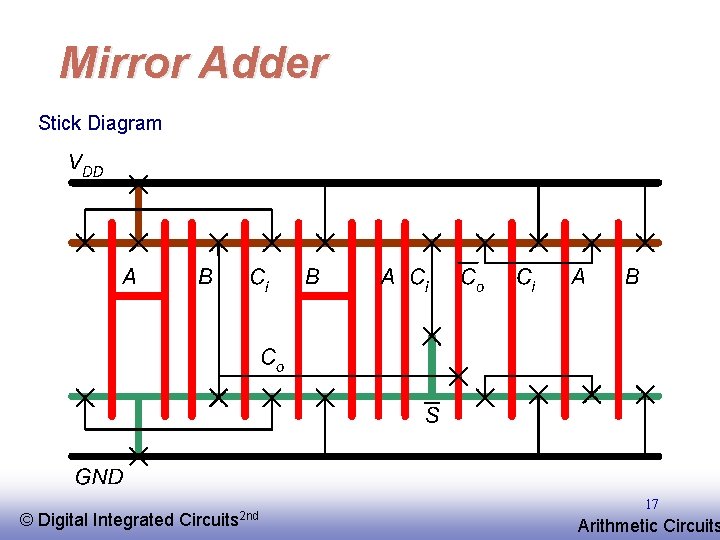
Mirror Adder Stick Diagram © EE 141 Digital Integrated Circuits 2 nd 17 Arithmetic Circuits

The Mirror Adder • The NMOS and PMOS chains are completely symmetrical. A maximum of two series transistors can be observed in the carrygeneration circuitry. • When laying out the cell, the most critical issue is the minimization of the capacitance at node Co. The reduction of the diffusion capacitances is particularly important. • The capacitance at node Co is composed of four diffusion capacitances, two internal gate capacitances, and six gate capacitances in the connecting adder cell. • The transistors connected to Ci are placed closest to the output. • Only the transistors in the carry stage have to be optimized for optimal speed. All transistors in the sum stage can be minimal size. © EE 141 Digital Integrated Circuits 2 nd 18 Arithmetic Circuits

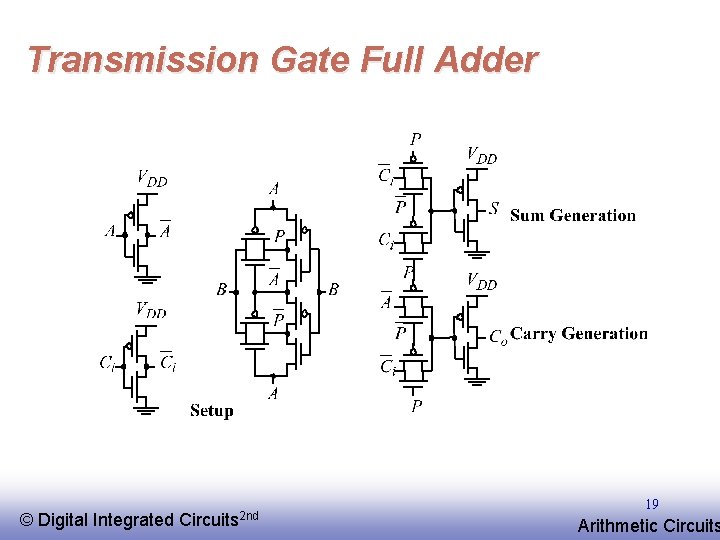
Transmission Gate Full Adder © EE 141 Digital Integrated Circuits 2 nd 19 Arithmetic Circuits

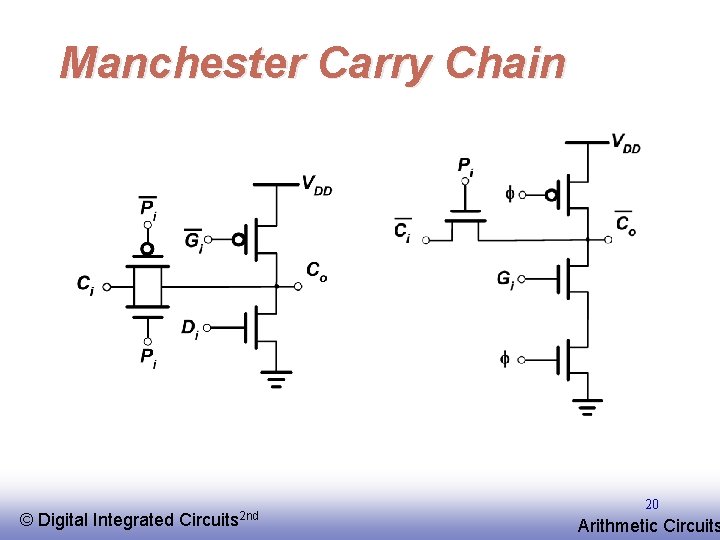
Manchester Carry Chain © EE 141 Digital Integrated Circuits 2 nd 20 Arithmetic Circuits

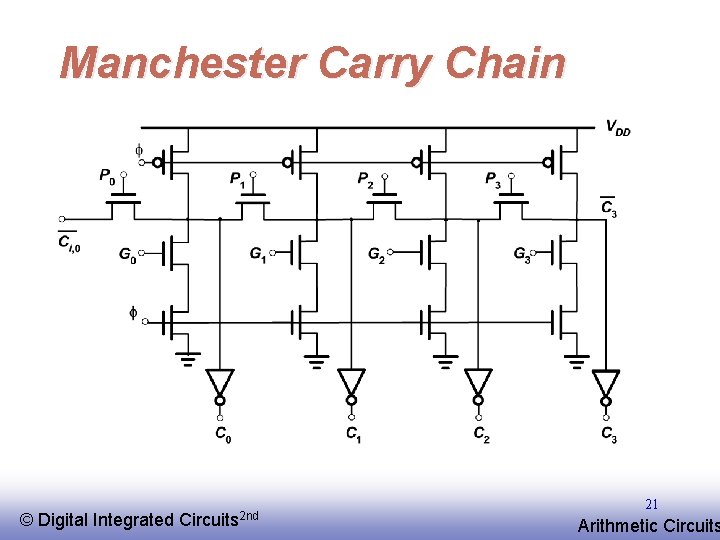
Manchester Carry Chain © EE 141 Digital Integrated Circuits 2 nd 21 Arithmetic Circuits

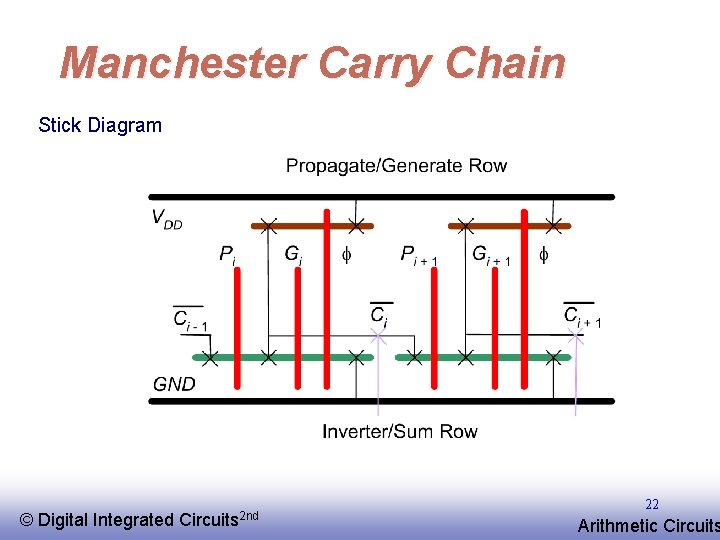
Manchester Carry Chain Stick Diagram © EE 141 Digital Integrated Circuits 2 nd 22 Arithmetic Circuits

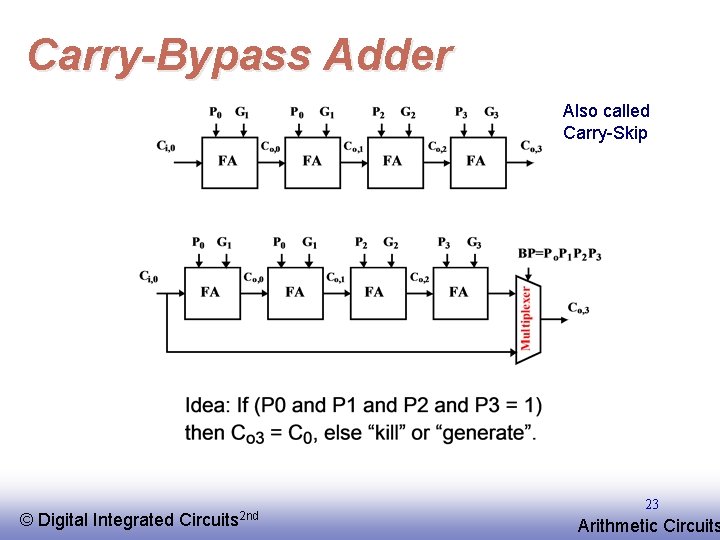
Carry-Bypass Adder Also called Carry-Skip © EE 141 Digital Integrated Circuits 2 nd 23 Arithmetic Circuits

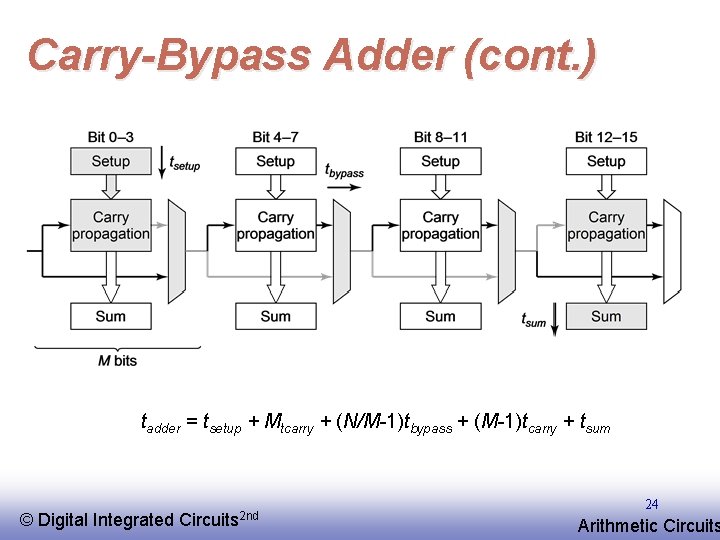
Carry-Bypass Adder (cont. ) tadder = tsetup + Mtcarry + (N/M-1)tbypass + (M-1)tcarry + tsum © EE 141 Digital Integrated Circuits 2 nd 24 Arithmetic Circuits

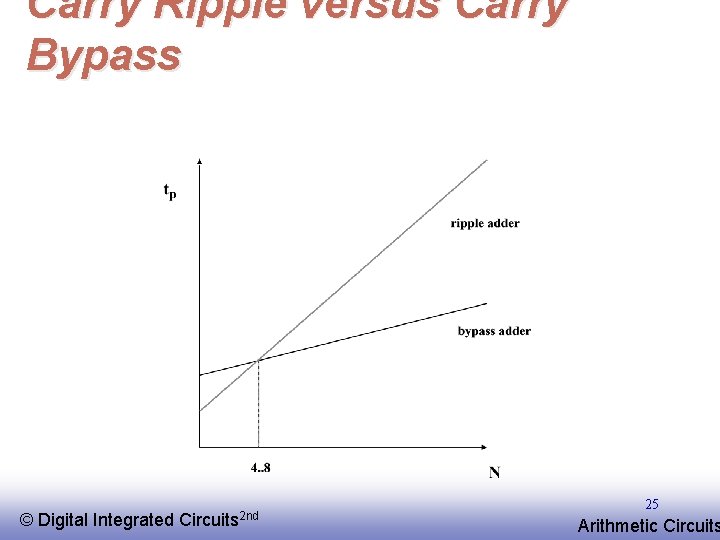
Carry Ripple versus Carry Bypass © EE 141 Digital Integrated Circuits 2 nd 25 Arithmetic Circuits

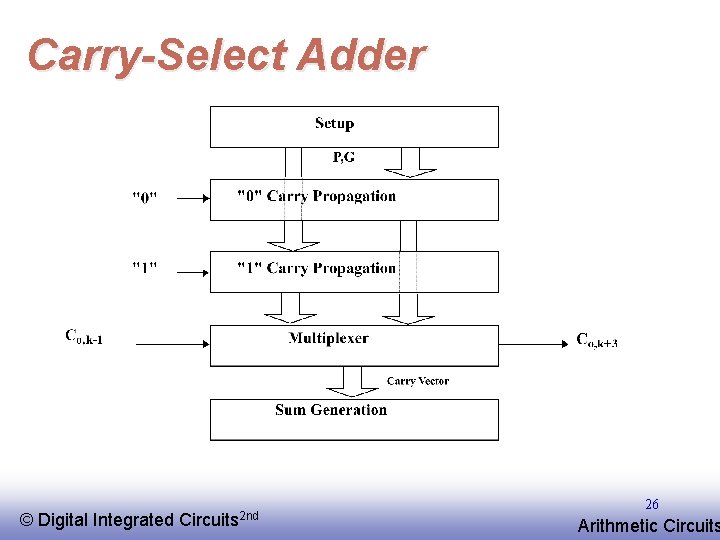
Carry-Select Adder © EE 141 Digital Integrated Circuits 2 nd 26 Arithmetic Circuits

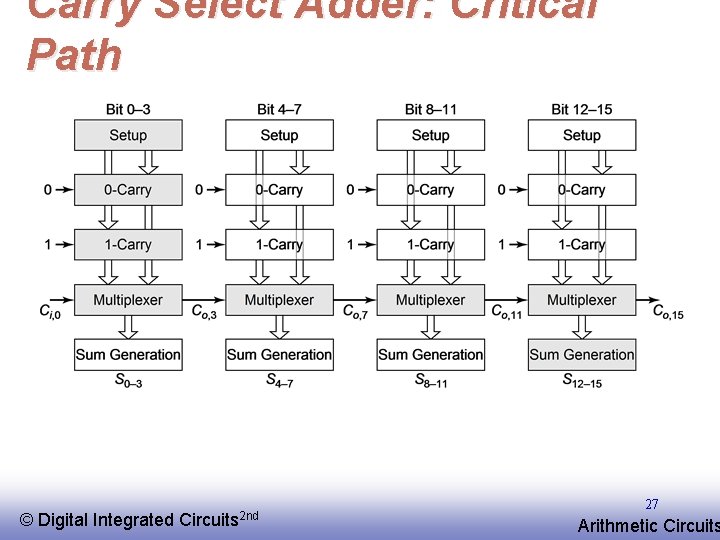
Carry Select Adder: Critical Path © EE 141 Digital Integrated Circuits 2 nd 27 Arithmetic Circuits

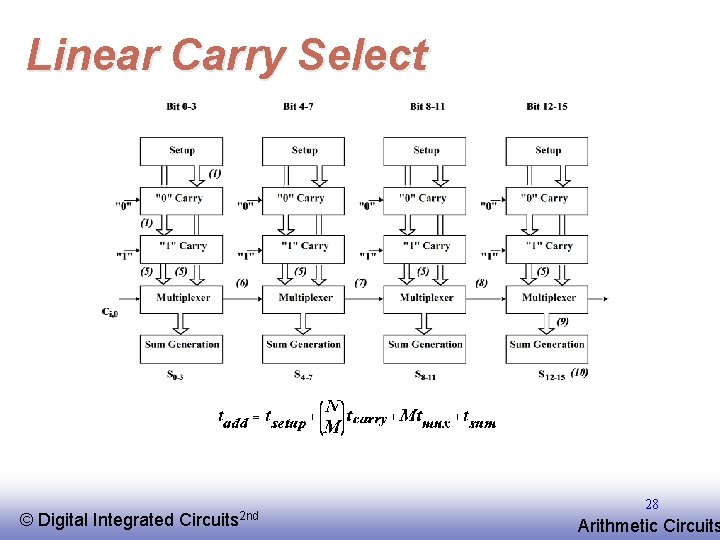
Linear Carry Select © EE 141 Digital Integrated Circuits 2 nd 28 Arithmetic Circuits

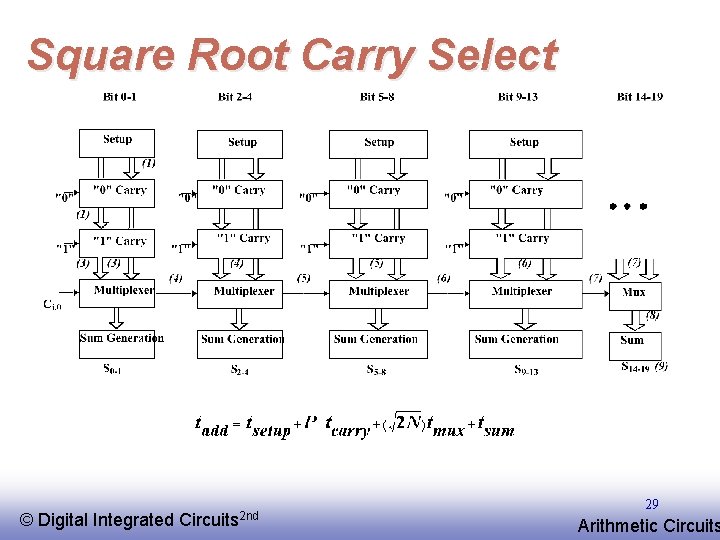
Square Root Carry Select © EE 141 Digital Integrated Circuits 2 nd 29 Arithmetic Circuits

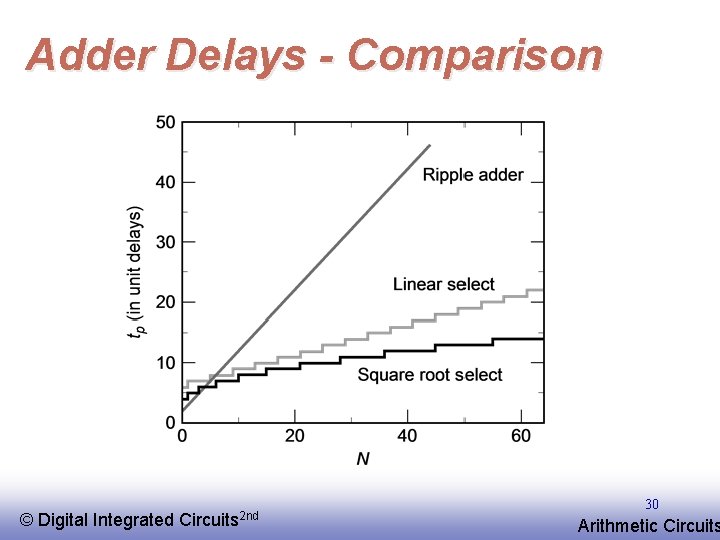
Adder Delays - Comparison © EE 141 Digital Integrated Circuits 2 nd 30 Arithmetic Circuits

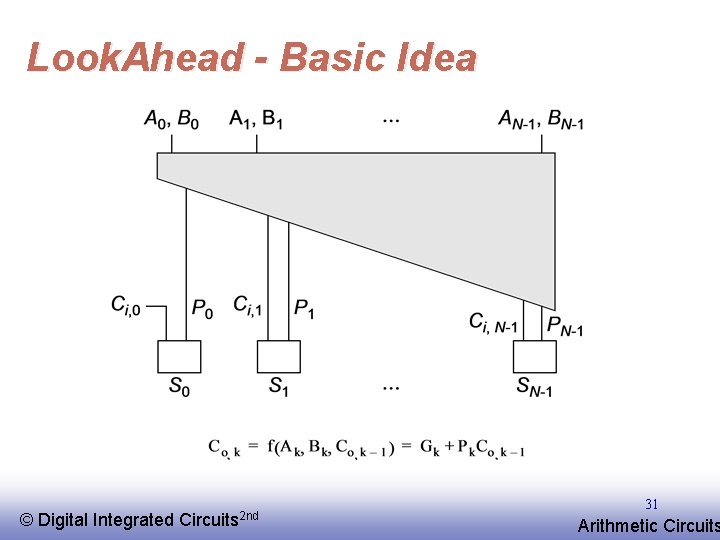
Look. Ahead - Basic Idea © EE 141 Digital Integrated Circuits 2 nd 31 Arithmetic Circuits

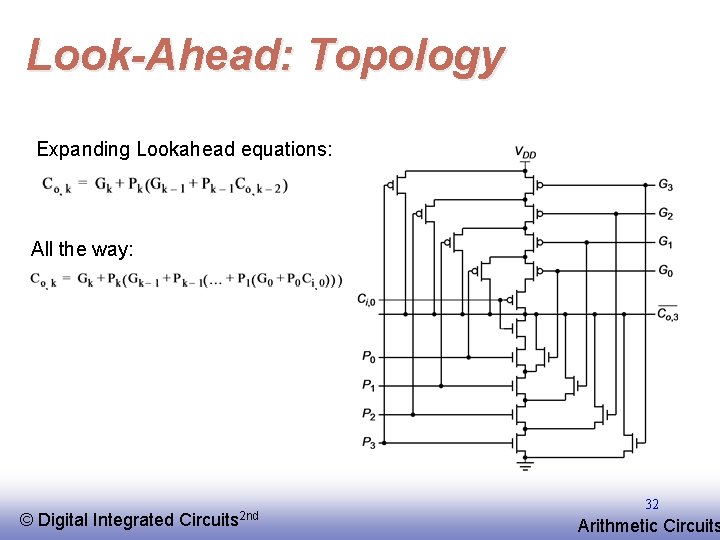
Look-Ahead: Topology Expanding Lookahead equations: All the way: © EE 141 Digital Integrated Circuits 2 nd 32 Arithmetic Circuits

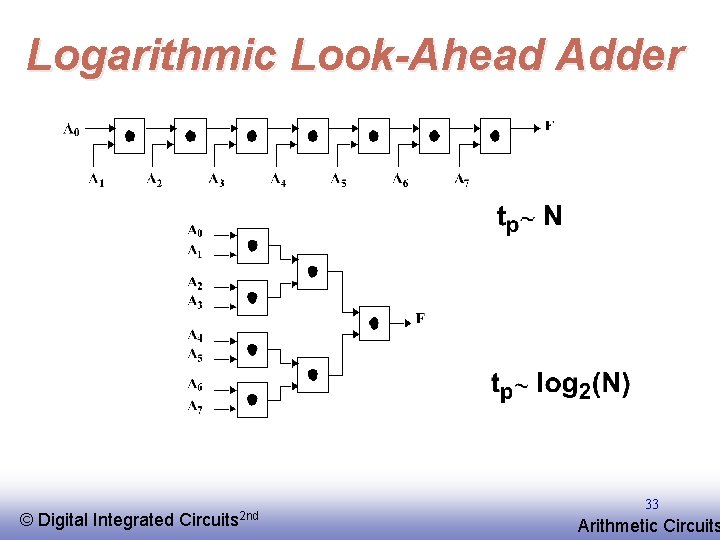
Logarithmic Look-Ahead Adder © EE 141 Digital Integrated Circuits 2 nd 33 Arithmetic Circuits

Carry Lookahead Trees Can continue building the tree hierarchically. © EE 141 Digital Integrated Circuits 2 nd 34 Arithmetic Circuits

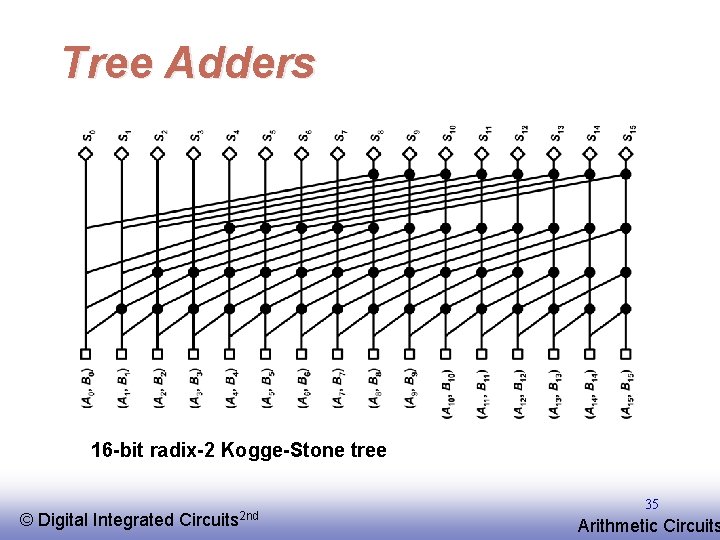
Tree Adders 16 -bit radix-2 Kogge-Stone tree © EE 141 Digital Integrated Circuits 2 nd 35 Arithmetic Circuits

Tree Adders 16 -bit radix-4 Kogge-Stone Tree © EE 141 Digital Integrated Circuits 2 nd 36 Arithmetic Circuits

Sparse Trees 16 -bit radix-2 sparse tree with sparseness of 2 © EE 141 Digital Integrated Circuits 2 nd 37 Arithmetic Circuits

Tree Adders Brent-Kung Tree © EE 141 Digital Integrated Circuits 2 nd 38 Arithmetic Circuits

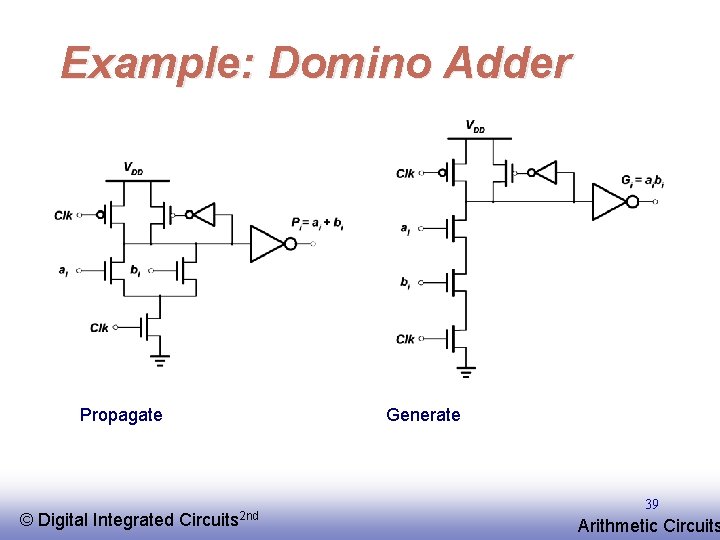
Example: Domino Adder Propagate © EE 141 Digital Integrated Generate Circuits 2 nd 39 Arithmetic Circuits

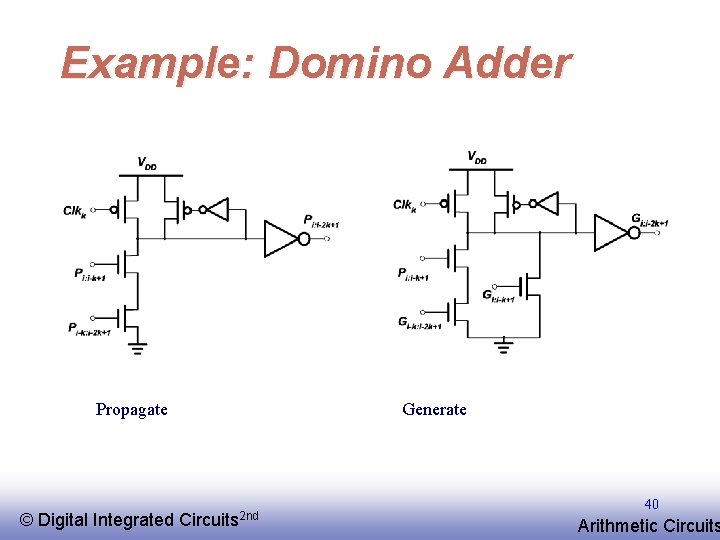
Example: Domino Adder Propagate © EE 141 Digital Integrated Generate Circuits 2 nd 40 Arithmetic Circuits

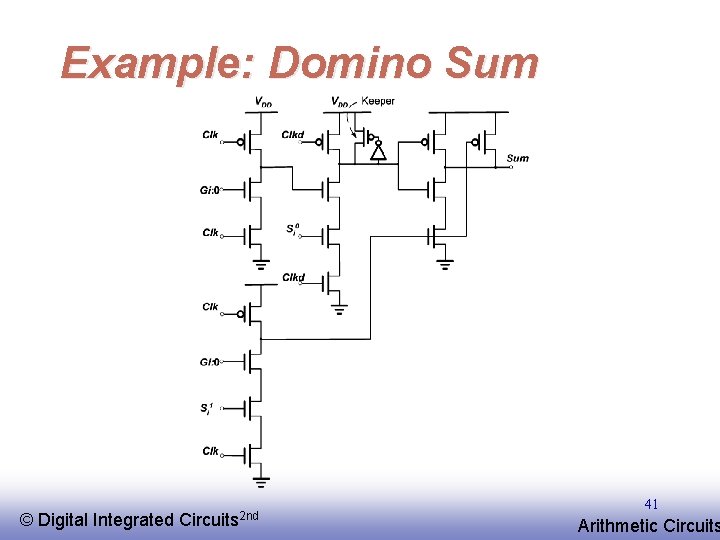
Example: Domino Sum © EE 141 Digital Integrated Circuits 2 nd 41 Arithmetic Circuits

Multipliers © EE 141 Digital Integrated Circuits 2 nd 42 Arithmetic Circuits

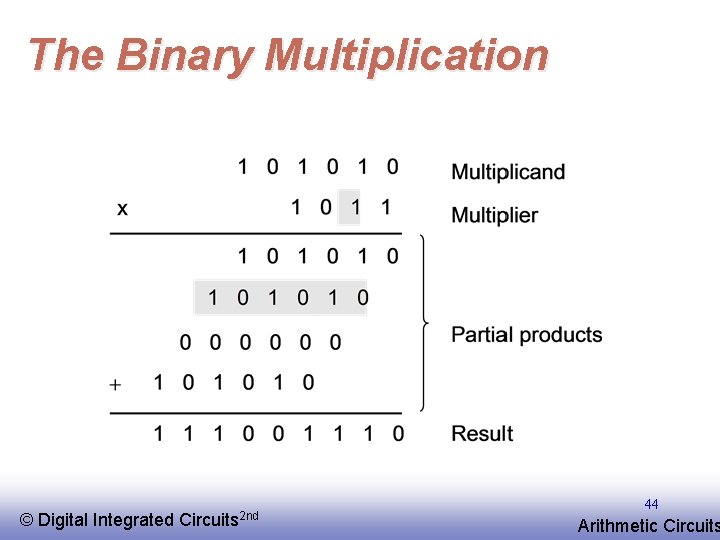
The Binary Multiplication © EE 141 Digital Integrated Circuits 2 nd 43 Arithmetic Circuits

The Binary Multiplication © EE 141 Digital Integrated Circuits 2 nd 44 Arithmetic Circuits

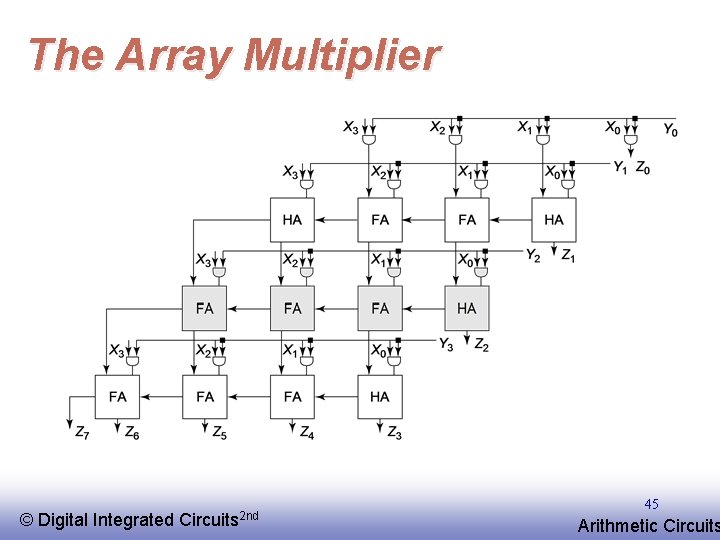
The Array Multiplier © EE 141 Digital Integrated Circuits 2 nd 45 Arithmetic Circuits

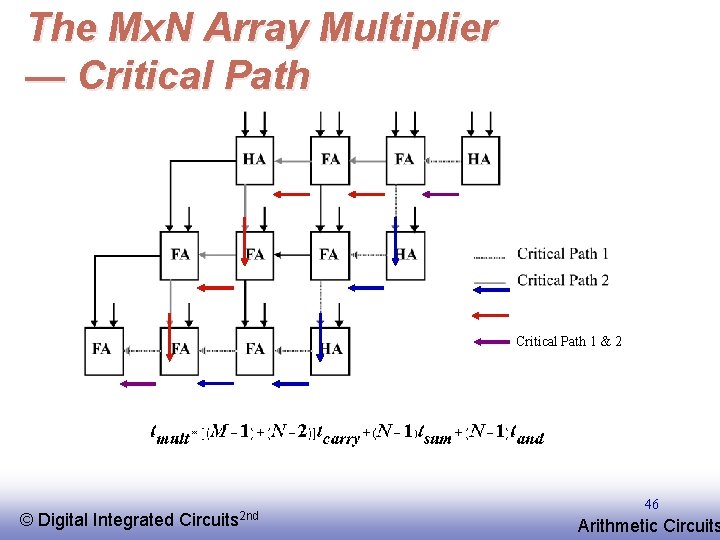
The Mx. N Array Multiplier — Critical Path 1 & 2 © EE 141 Digital Integrated Circuits 2 nd 46 Arithmetic Circuits

Carry-Save Multiplier © EE 141 Digital Integrated Circuits 2 nd 47 Arithmetic Circuits

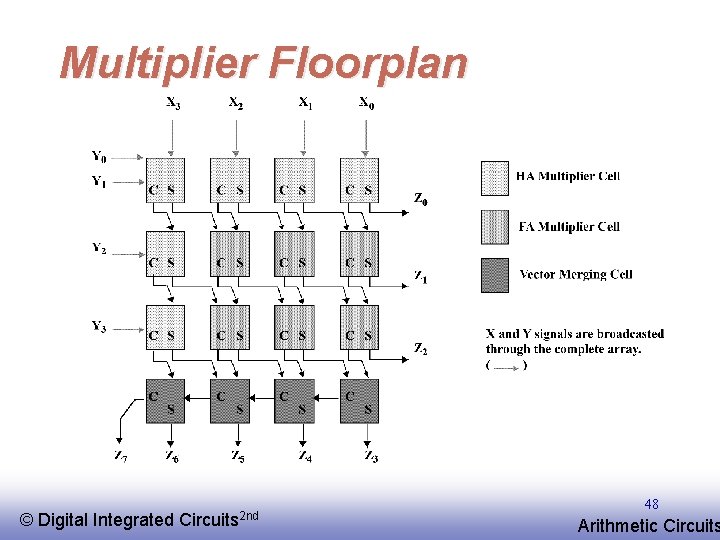
Multiplier Floorplan © EE 141 Digital Integrated Circuits 2 nd 48 Arithmetic Circuits

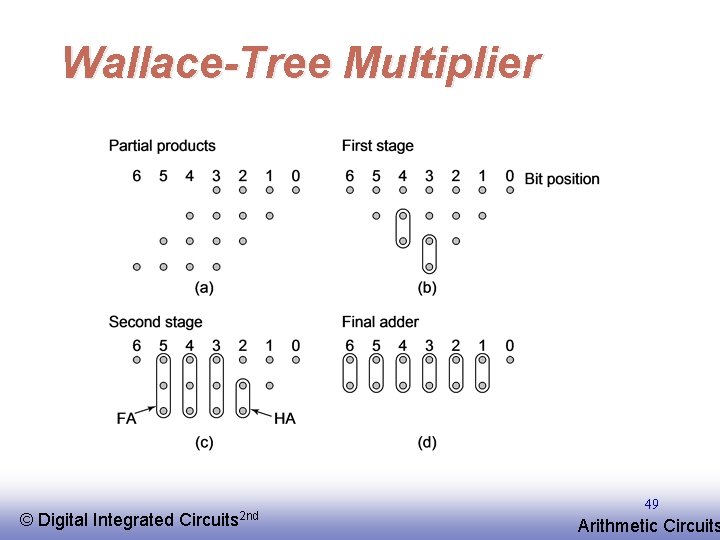
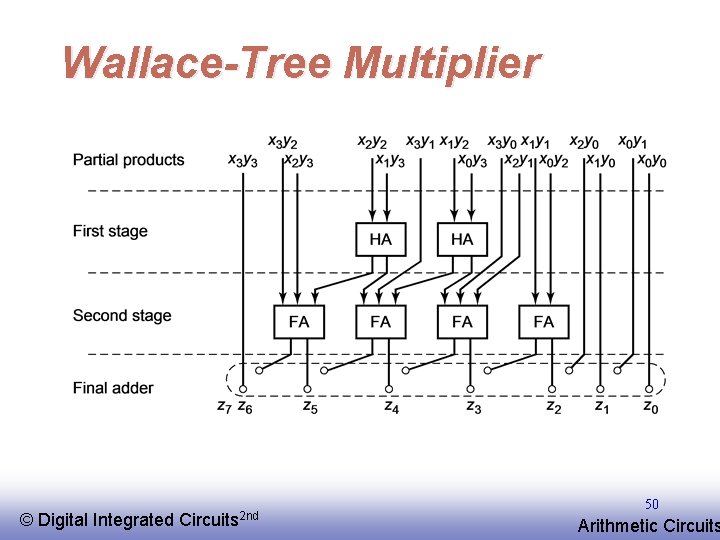
Wallace-Tree Multiplier © EE 141 Digital Integrated Circuits 2 nd 49 Arithmetic Circuits

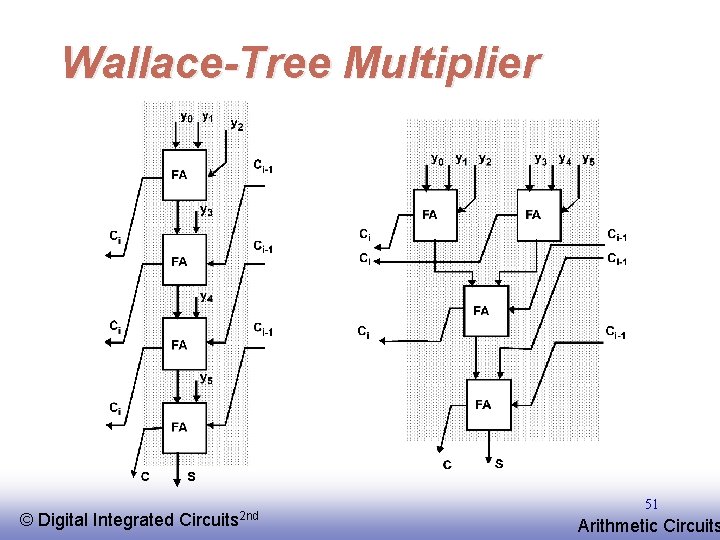
Wallace-Tree Multiplier © EE 141 Digital Integrated Circuits 2 nd 50 Arithmetic Circuits

Wallace-Tree Multiplier © EE 141 Digital Integrated Circuits 2 nd 51 Arithmetic Circuits

Multipliers —Summary © EE 141 Digital Integrated Circuits 2 nd 52 Arithmetic Circuits

Shifters © EE 141 Digital Integrated Circuits 2 nd 53 Arithmetic Circuits

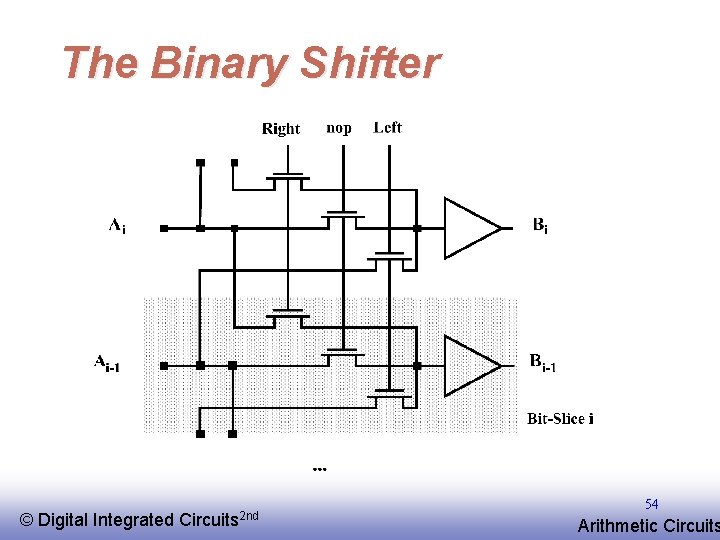
The Binary Shifter © EE 141 Digital Integrated Circuits 2 nd 54 Arithmetic Circuits

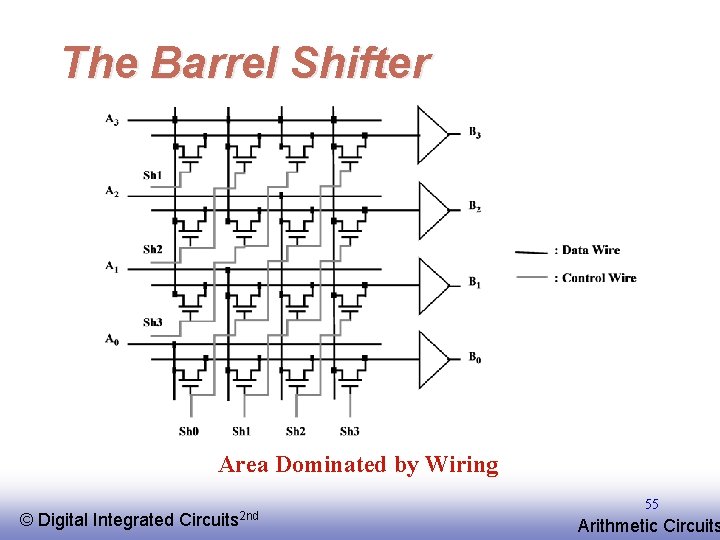
The Barrel Shifter Area Dominated by Wiring © EE 141 Digital Integrated Circuits 2 nd 55 Arithmetic Circuits

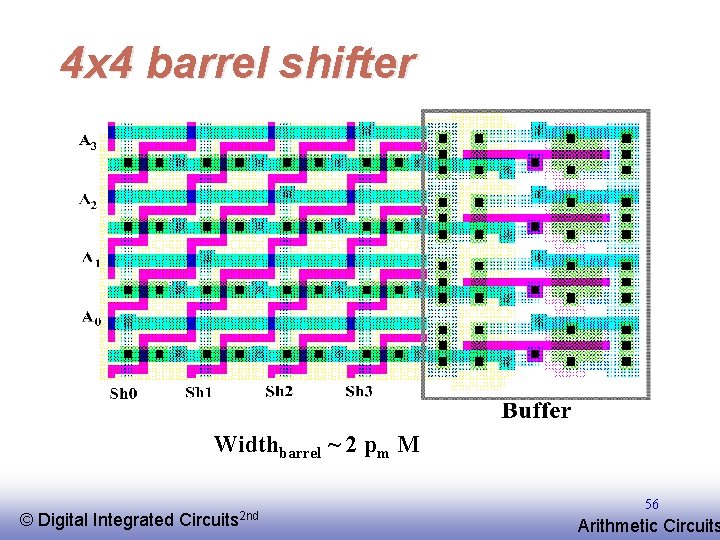
4 x 4 barrel shifter Widthbarrel ~ 2 pm M © EE 141 Digital Integrated Circuits 2 nd 56 Arithmetic Circuits

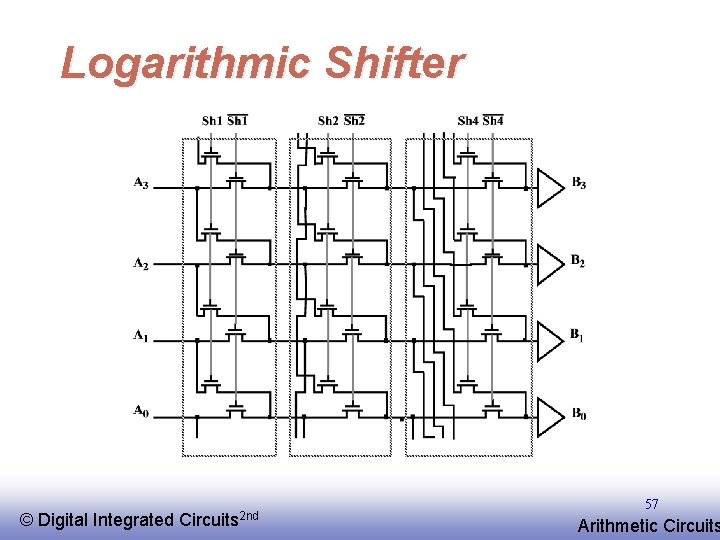
Logarithmic Shifter © EE 141 Digital Integrated Circuits 2 nd 57 Arithmetic Circuits

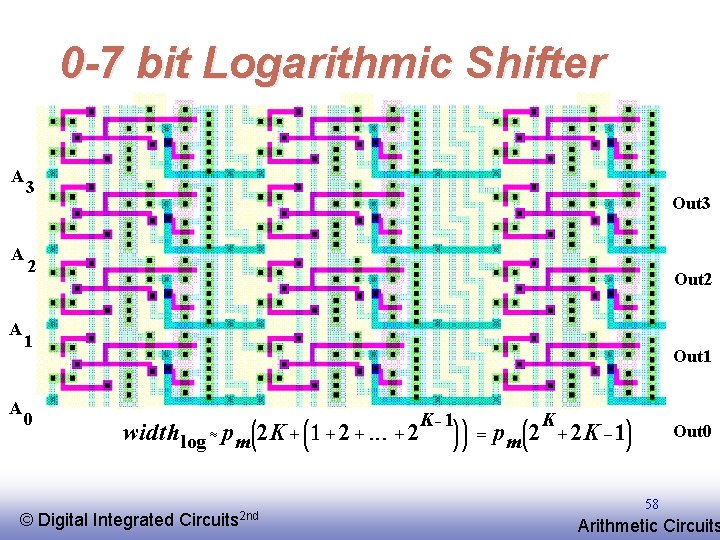
0 -7 bit Logarithmic Shifter A A 3 Out 3 2 Out 2 1 Out 1 0 © EE 141 Digital Integrated Out 0 Circuits 2 nd 58 Arithmetic Circuits