Digital Information Storage Contents Binary vs decimal Advantages

Digital Information Storage Contents: • Binary vs decimal • Advantages of binary • CDs and DVDs

Binary: 0 1 2 3 4 5 6 7 8 9 10 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 Bin to Dec: 1101 = 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 = 13 237 to binary: Dec to Bin: 237 -1 x 128 109 -1 x 64 45 - 1 x 32 13 - 0 x 16 13 - 1 x 8 5 - 1 x 4 1 - 0 x 2 1 - 1 x 1 237 = 11101101 Place 128 64 32 16 8 4 2 1 1 - msb 1 1 0 1 - lsb TOC

Whiteboards: Binary Conversions 1|2|3|4 TOC

Convert 11001 to decimal: 11001 = 1 x 24 + 1 x 23 + 0 x 22 + 0 x 21 + 1 x 20 = 25 25 W

Convert 11011010 to decimal: 11011010 = 1 x 27 + 1 x 26 + 0 x 25 + 1 x 24 + 1 x 23 + 0 x 22 + 1 x 21 + 0 x 20 = 218 W

Convert 175 to binary: 175: Dec to Bin: 175 -1 x 128 47 -0 x 64 47 - 1 x 32 15 - 0 x 16 15 - 1 x 8 7 - 1 x 4 3 - 1 x 2 1 - 1 x 1 Place 128 64 32 16 8 4 2 1 1 - msb 0 1 1 1 1 - lsb 175 = 10101111 W

Convert 198 to binary: 198: Dec to Bin: 175 -1 x 128 70 - 1 x 64 6 - 0 x 32 6 - 0 x 16 6 - 0 x 8 6 - 1 x 4 2 - 1 x 2 0 - 0 x 1 Place 128 64 32 16 8 4 2 1 1 - msb 1 0 0 0 1 1 0 - lsb 198 = 11000110 W

Advantages of Binary Analog storage: Signal varies continuously Ex – magnetic tape Degradation Taping a record or CD Digital storage: 1 vs 0 less subtle Degradation Copying a CD Error Correction TOC

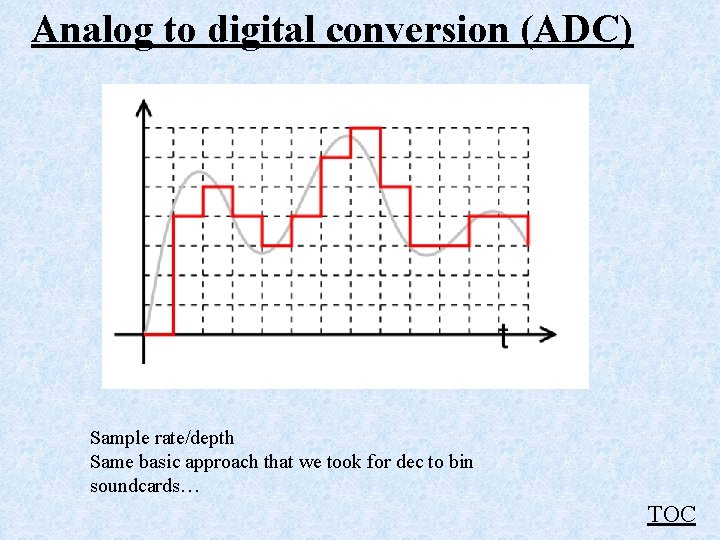
Analog to digital conversion (ADC) Sample rate/depth Same basic approach that we took for dec to bin soundcards… TOC

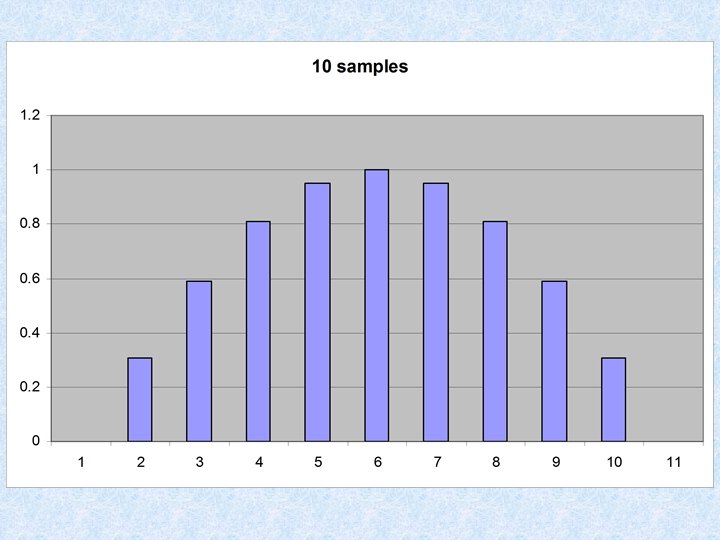
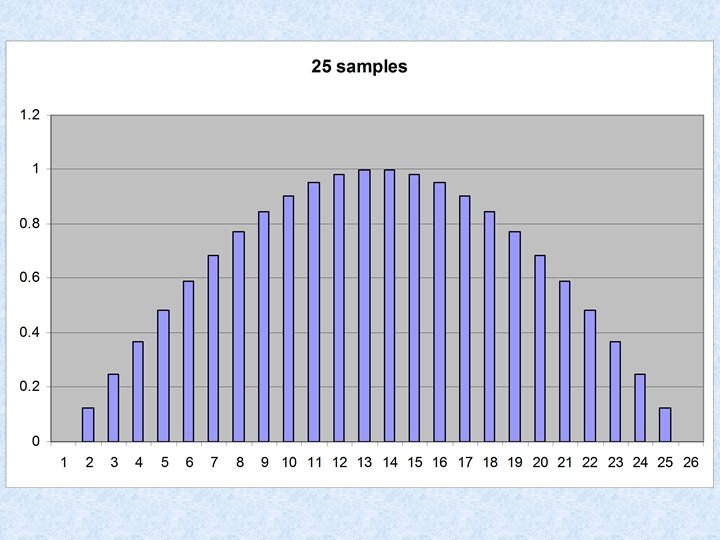
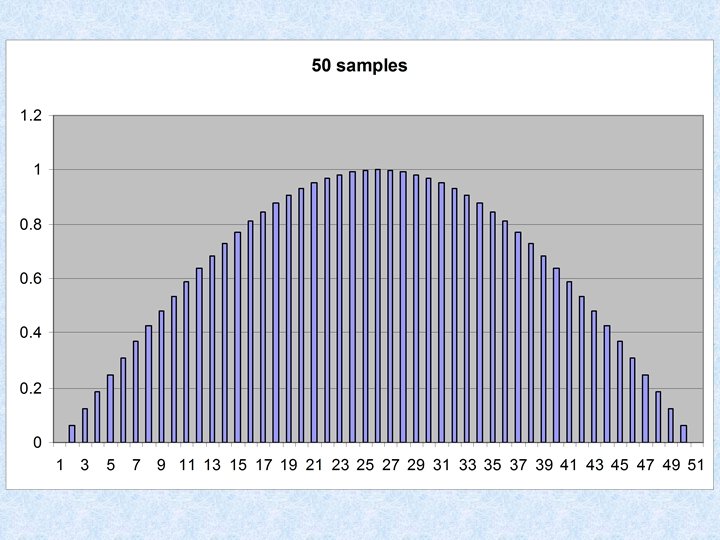
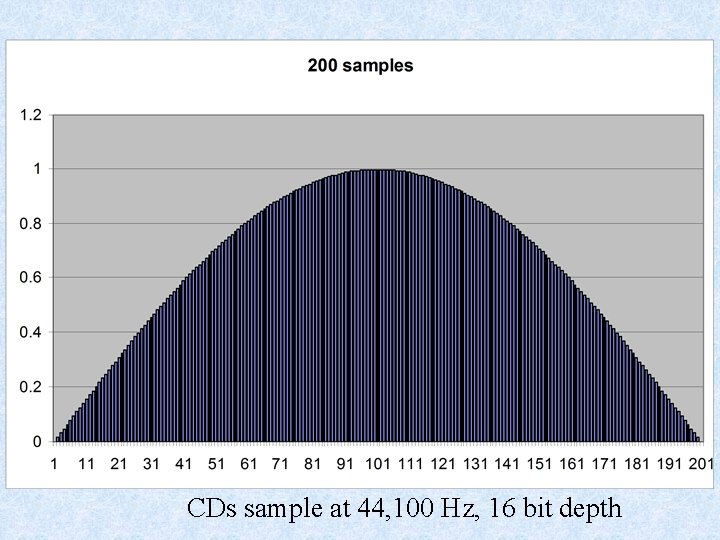
CDs sample at 44, 100 Hz, 16 bit depth

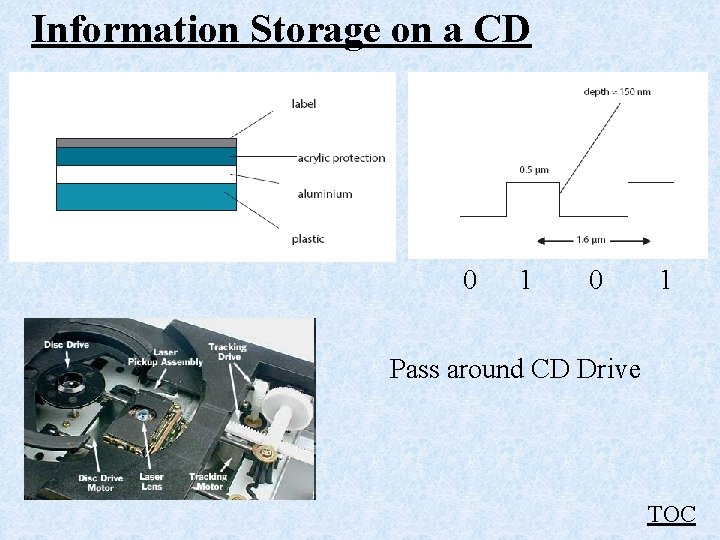
Information Storage on a CD 0 1 Pass around CD Drive TOC

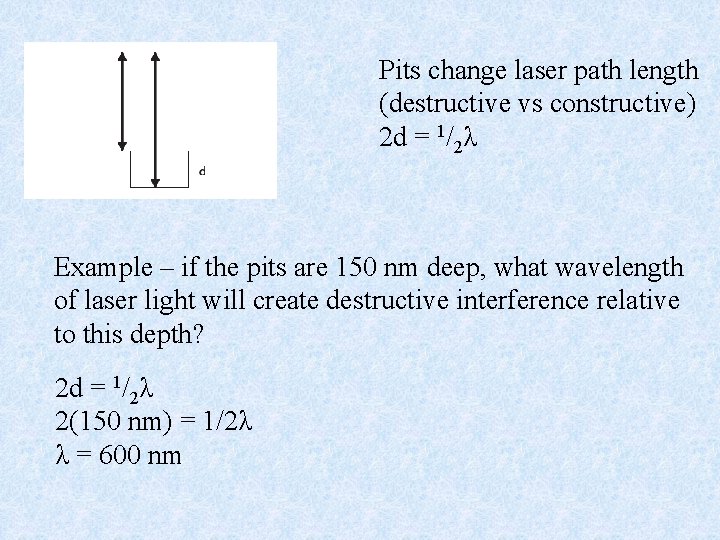
Pits change laser path length (destructive vs constructive) 2 d = 1/2λ Example – if the pits are 150 nm deep, what wavelength of laser light will create destructive interference relative to this depth? 2 d = 1/2λ 2(150 nm) = 1/2λ λ = 600 nm

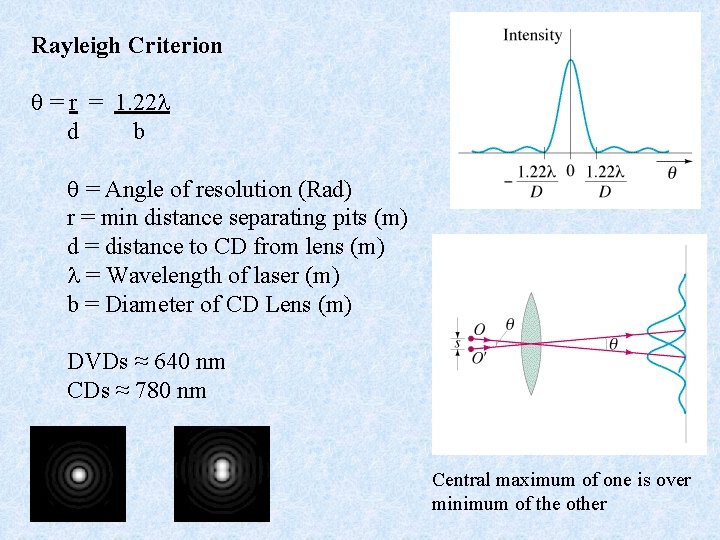
Rayleigh Criterion = r = 1. 22 d b = Angle of resolution (Rad) r = min distance separating pits (m) d = distance to CD from lens (m) = Wavelength of laser (m) b = Diameter of CD Lens (m) DVDs ≈ 640 nm CDs ≈ 780 nm Central maximum of one is over minimum of the other

8 bits bytes are actually mapped to 14 bits on CDs

Whiteboards: Pits and interference 1|2|3 TOC

If an optical drive uses light that is 340 nm, what pit depth would create destructive interference? 2 d = 1/2λ = 1/2(340 nm) d = 85 nm W

A CD has pits that are 125 nm deep. What wavelength of laser light would generate destructive interference relative to that depth? 2(125 nm) = 1/2λ λ = 500 nm W

Example: DVDs have pits that are about 0. 74μm apart. If the lens has a diameter of 4. 2 mm, and the laser has a wavelength of 780 nm, what must be the maximum distance from the lens to the disc so that the reader can resolve the pits? = r = 1. 22 d b d = (0. 74 E-6)(4. 2 E-3)/(1. 22*780 E-9) =. 003266… 3. 3 mm W

Other methods of data storage • RAM/cache • Flash memory/Core • Magnetic • CD/DVD