Digital Image Processing Pattern Analysis CSCE 563 Geometric

Digital Image Processing & Pattern Analysis (CSCE 563) Geometric Transformations Prof. Amr Goneid Department of Computer Science & Engineering The American University in Cairo

Geometric Transformations Image Cropping Interpolation Image Resizing Image Rotation Affine Transform Image Registration Prof. Amr Goneid, AUC 2

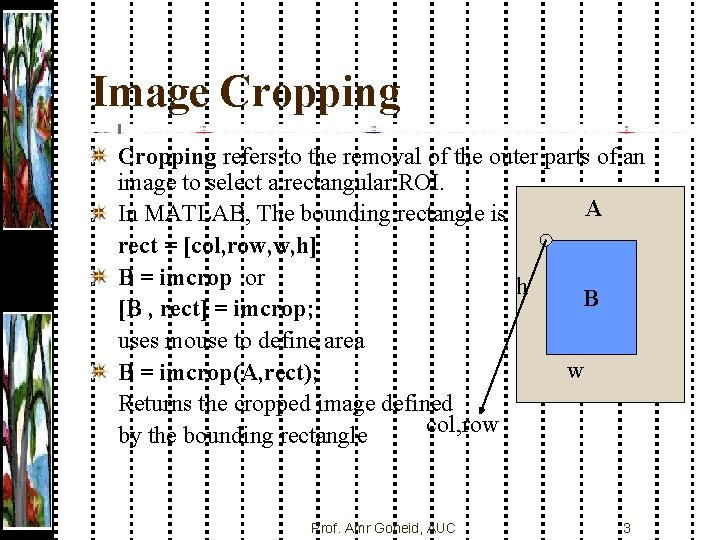
Image Cropping refers to the removal of the outer parts of an image to select a rectangular ROI. A In MATLAB, The bounding rectangle is rect = [col, row, w, h] B = imcrop or h B [B , rect] = imcrop; uses mouse to define area w B = imcrop(A, rect); Returns the cropped image defined col, row by the bounding rectangle Prof. Amr Goneid, AUC 3

Example: Top Left Quadrant load treesc; [n, m] = size(X); rect = [1, 1, m/2, n/2]; B = imcrop(X, rect); subplot(2, 1, 1); imshow(X, map); subplot(2, 1, 2); imshow(B, map); Prof. Amr Goneid, AUC 4

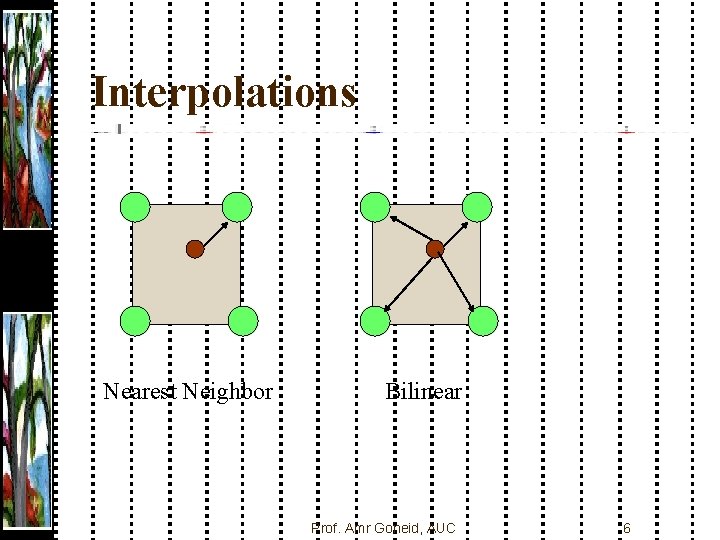
Interpolation 2 -D Interpolation Used in resizing and rotation Nearest Neighbor Interpolation (nearest) Bilinear Interpolation (bilinear) Bicubic Interpolation (bicubic) Prof. Amr Goneid, AUC 5

Interpolations Nearest Neighbor Bilinear Prof. Amr Goneid, AUC 6

Example: Bilinear interpolation (From Wikipedia) bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables on a regular grid. The key idea is to perform linear interpolation first in one direction, and then again in the other direction. to find the value of the unknown function f at the point P = (x, y). It is assumed that we know the value of f at the four points Q 11 = (x 1, y 1), Q 12 = (x 1, y 2), Q 21 = (x 2, y 1), and Q 22 = (x 2, y 2). Prof. Amr Goneid, AUC 7

Example: Bilinear interpolation Linear interpolation in the x-direction interpolating in the y-direction This yields Prof. Amr Goneid, AUC 8

Bilinear interpolation In a coordinate system in which the four points are at (0, 0), (0, 1), (1, 0), and (1, 1), then in matrix form The result of bilinear interpolation is independent of the order of interpolation. If we had first performed the linear interpolation in the y-direction and then in the x-direction, the resulting approximation would be the same. Prof. Amr Goneid, AUC 9

Resizing using Interpolation Resize by 183% No Interpolation Original With Interpolation Prof. Amr Goneid, AUC 10

Resizing B = imresize(A, m, ’method’) m = ratio Example: load clownc; B = imresize(X, 3, ’nearest’); C = imresize(X, 0. 3, ’nearest’); subplot(3, 1, 1); imshow(X, map); subplot(3, 1, 2); imshow(B, map); subplot(3, 1, 3); imshow(C, map); Prof. Amr Goneid, AUC 11

Rotation B = imrotate(A, angle); or B = imrotate(A, angle, ’crop’); angle is anti-clockwise (degrees) Example: load amber 256; C = imrotate(X, 45, 'crop'); subplot(2, 1, 1); imshow(X, map); subplot(2, 1, 2); imshow(C, map); Prof. Amr Goneid, AUC 12

Affine Transform Let f be an image defined over (w, z) coordinate system, g is a geometric transformation of f with: (x , y) = T{(w , z)} Example: (x , y) = T{(w , z)} = (w/2 , z/2) This is shrinking f by ½ in both spatial dimensions. Prof. Amr Goneid, AUC 13

Affine Transform Prof. Amr Goneid, AUC 14

Affine Transform Commonly used transform is the Affine Transform, in matrix form: [x y 1] = [w z 1] T = [w z 1] Can produce scaling, translation, rotation and shear. Prof. Amr Goneid, AUC 15

Affine Transform Prof. Amr Goneid, AUC 16

Affine Transform MATLAB Example (scaling): T = [2 0 0; 0 3 0; 0 0 1]; tform = maketform(‘affine’ , T); wz = [1 1; 3 2]; xy = tformfwd(wz , tform); Result is xy = [2 3; 6 6]; Also: wz 2 = tforminv(xy , tform); % inverse transform Prof. Amr Goneid, AUC 17

Affine Transform Examples: • • • Scale Horizontally by 3 and vertically by 2 T 1 = [3 0 0; 0 2 0; 0 0 1]; Shear T 2 = [1 0 0; 0. 2 1 0; 0 0 1]; Tscale = [1. 5 0 0; 0 2 0; 0 0 1]; Trot = [cos(pi/4) sin(pi/4) 0; -sin(pi/4) cos(pi/4) 0; 0 0 1]; Tshear = [1 0 0; 0. 2 1 0; 0 0 1]; T 3 = Tscale * Trot * Tshear; Prof. Amr Goneid, AUC 18

Affine Transform Prof. Amr Goneid, AUC 19

Affine Transform Prof. Amr Goneid, AUC 20

Image Registration Image registration is the process of overlaying two or more images of the same scene taken at different times, from different viewpoints, and/or by different sensors. Applications: Change detection, Image fusion, Target recognition, Target localization, Depth perception, Image mosaicing, Motion estimation Prof. Amr Goneid, AUC 21

Image Registration CP CP Prof. Amr Goneid, AUC 22

Image Registration CP CP Prof. Amr Goneid, AUC 23

Image Registration (References) Image registration methods: a survey Barbara Zitova´*, Jan Flusser http: //library. utia. cas. cz/prace/20030125. pdf Image Registration http: //tango. andrew. cmu. edu/~gustavor/42431 -introbioimaging/readings/ch 8. pdf Image Registration in MATLAB http: //www. mathworks. com/help/toolbox/images/f 20 -9579. html Prof. Amr Goneid, AUC 24