Digital Image Processing Lecture 19 Segmentation Morphological Watersheds

Digital Image Processing Lecture 19: Segmentation: Morphological Watersheds Prof. Charlene Tsai 1

Introduction n Review: We have done q q q n Detection of discontinuities Thresholding Region processing Morphological watersheds embodies properties from other 3 approaches, therefore more superior. 2

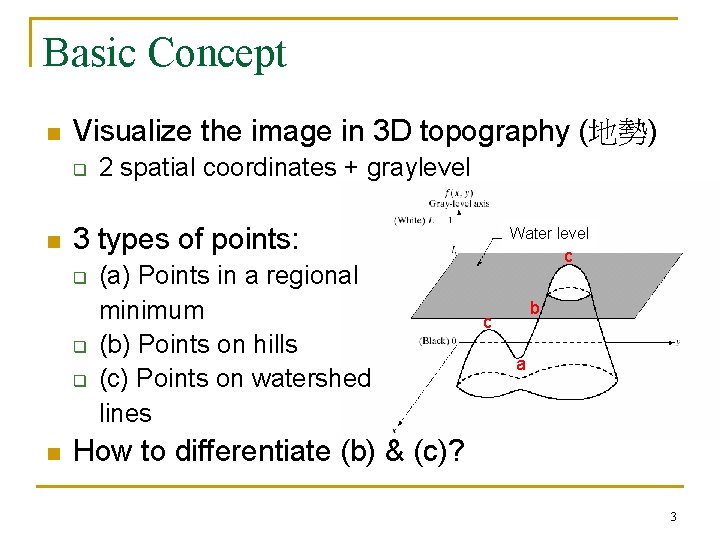
Basic Concept n Visualize the image in 3 D topography (地勢) q n 3 types of points: q q q n 2 spatial coordinates + graylevel (a) Points in a regional minimum (b) Points on hills (c) Points on watershed lines Water level c b c a How to differentiate (b) & (c)? 3

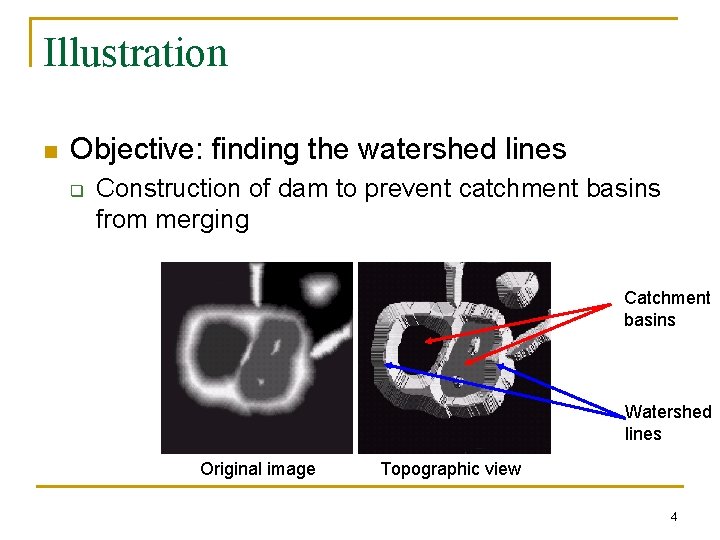
Illustration n Objective: finding the watershed lines q Construction of dam to prevent catchment basins from merging Catchment basins Watershed lines Original image Topographic view 4

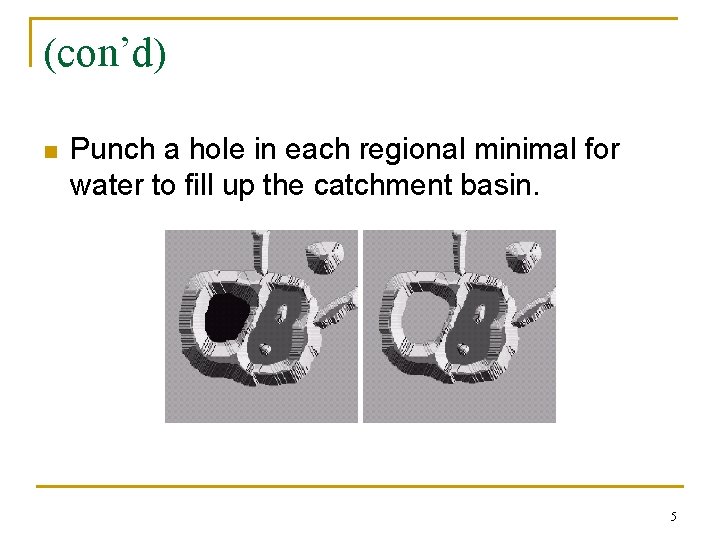
(con’d) n Punch a hole in each regional minimal for water to fill up the catchment basin. 5

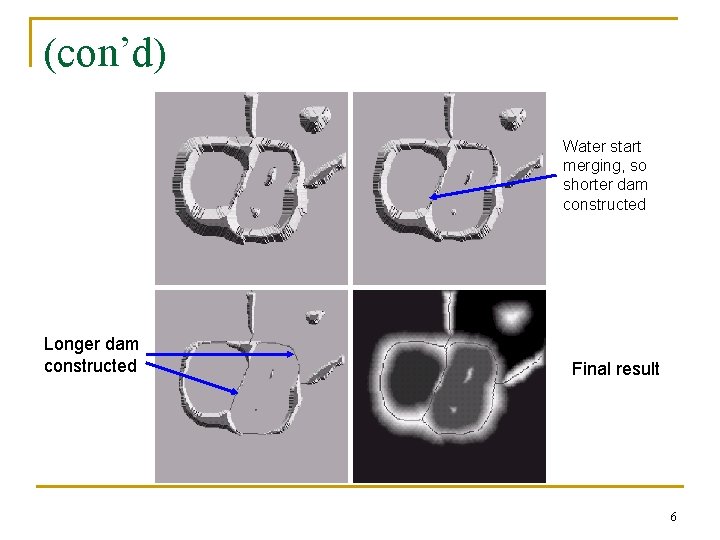
(con’d) Water start merging, so shorter dam constructed Longer dam constructed Final result 6

Aside n Watershed algorithm is often applied to the gradient of an image, rather than to the image itself. q q Regional minima of catchment basins correlate nicely with the small value of the gradient corresponding the objects of interest Boundaries are highlighted as the watershed lines. 7

Watershed Segmentation Algorithm n Starting with the notation: q q g(x, y) is the image with min and max the lowest and highest graylevel, respectively M 1, M 2, … MR be the regional minima T[n]={ (s, t) | g(s, t)<n } Cn(Mi) is the set of (s, t) in the catchment basin of Mi that are flooded at stage n. q n C[n-1] is a subset of C[n] and C[n] is subset of T[n]. So it implies that q Each connected component (CC) of C[N-1] is contained in exactly one CC of T[n]. 8

Flooding n n Initialization: C[min+1]=T[min+1] Obtain C[n] from C[n-1] (recursively): q q Let Q be the set of CC in T[n], and 3 possibilities for : (a) empty (b) containing one CC of C[n-1] (c) containing more than one CC of C[n-1] 9

Constructing C[n] n Scenario (a) [empty]: a new minimum is found q n Scenario (b) [containing 1 CC]: q lies in the catchment basin of some regional minimum q n q is incorporated into C[n-1] to form C[n] Scenario (c) [containing 1+ CC], part of the watershed line is encountered. q A dam must be build within q to prevent overflow between the catchment basins. 10

Dam Construction of height max+1 In C[n-1] q Scenario (c) 11

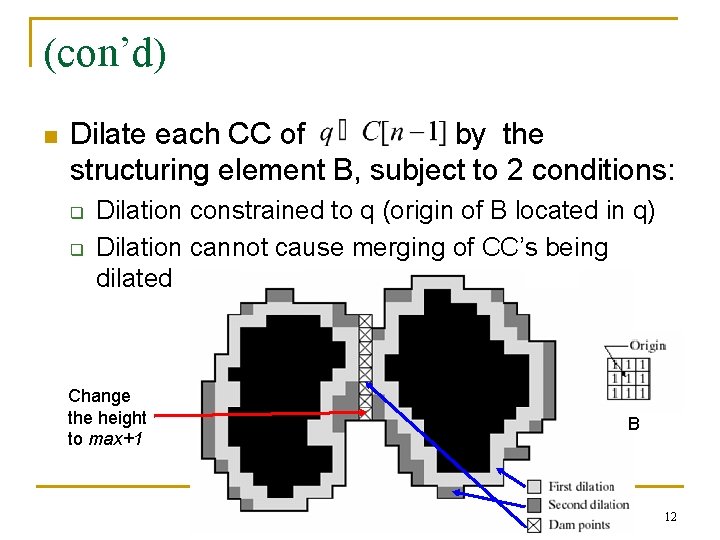
(con’d) n Dilate each CC of by the structuring element B, subject to 2 conditions: q q Dilation constrained to q (origin of B located in q) Dilation cannot cause merging of CC’s being dilated Change the height to max+1 B 12

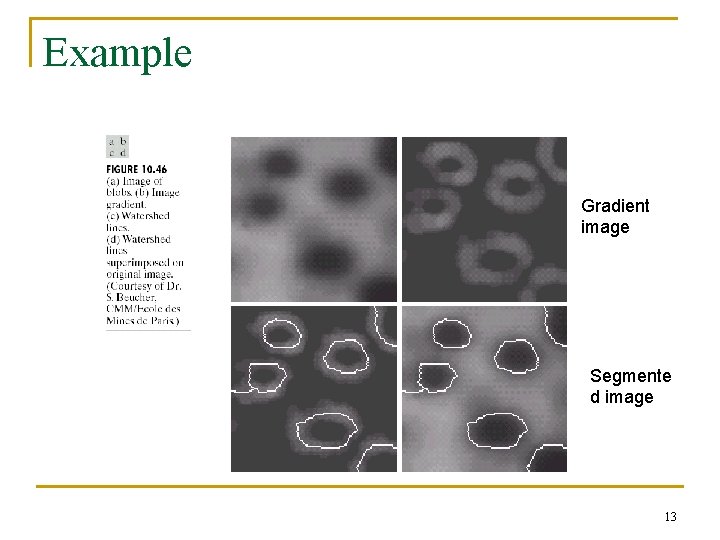
Example Gradient image Segmente d image 13

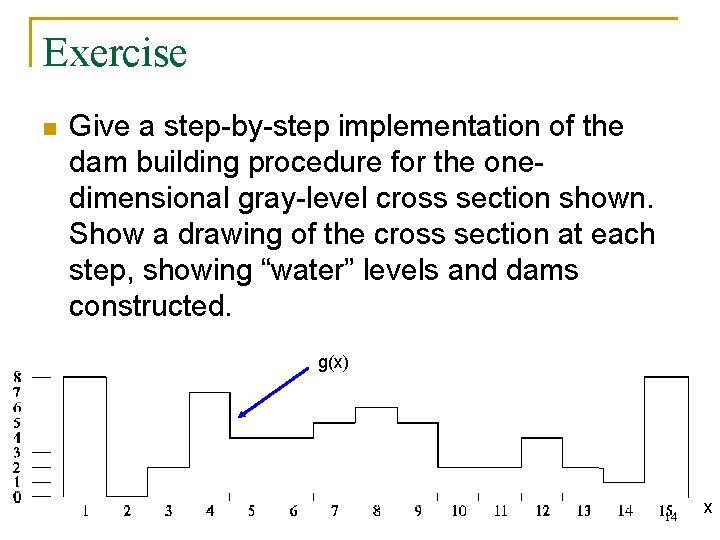
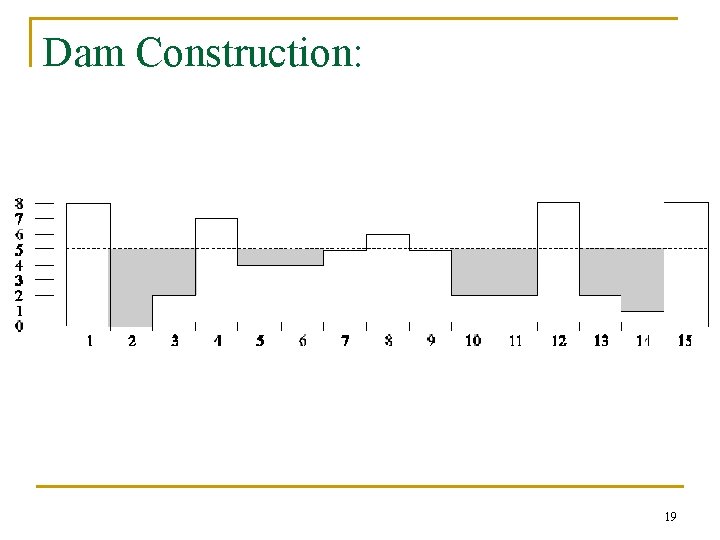
Exercise n Give a step-by-step implementation of the dam building procedure for the onedimensional gray-level cross section shown. Show a drawing of the cross section at each step, showing “water” levels and dams constructed. g(x) 14 x

Step 1 (n=1): n n n T[1]=? C[1]=? Q[1]=? 15

Step 2 (n=2): n n n T[2]=? Q[2]=? C[2]=? 16

Step 3 (n=3, 4): n n T[3]=? Q[3]=? C[4]=? 17

Step 5 (n=5): n n n T[5]=? Q[5]=? C[5]=? 18

Dam Construction: 19