Digital Image Processing Chapter 4 Image Enhancement in































- Slides: 43

Digital Image Processing Chapter # 4 Image Enhancement in Frequency Domain

ALI JAVED Lecturer SOFTWARE ENGINEERING DEPARTMENT U. E. T TAXILA Email: : alijaved@uettaxila. edu. pk Office Room #: : 7

Introduction

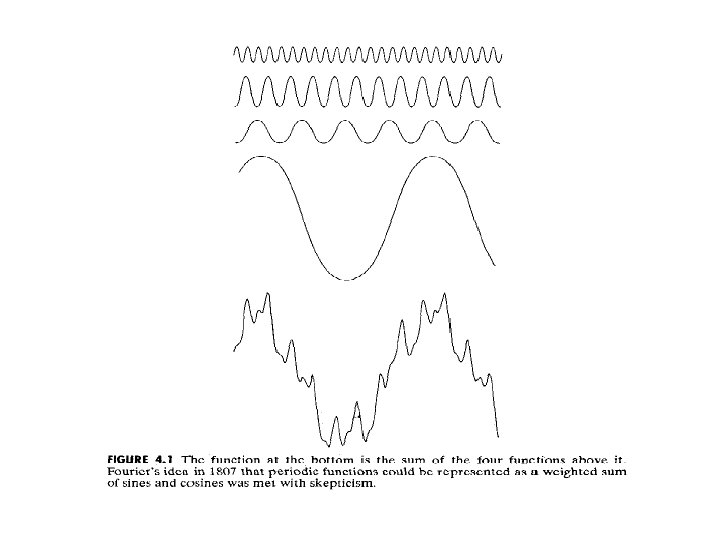
Background (Fourier Series) § Any function that periodically repeats itself can be expressed as the sum of sines and cosines of different frequencies each multiplied by a different coefficient § This sum is known as Fourier Series § It does not matter how complicated the function is; as long as it is periodic and meet some mild conditions it can be represented by such as a sum § It was a revolutionary discovery


Background (Fourier Transform) § Even functions that are not periodic can be expressed as the integrals of sines and cosines multiplied by a weighing function § This is known as Fourier Transform § A function expressed in either a Fourier Series or transform can be reconstructed completely via an inverse process with no loss of information § This is one of the important characteristics of these representations because they allow us to work in the Fourier Domain and then return to the original domain of the function

Fourier Transform • ‘Fourier Transform’ transforms one function into another domain , which is called the frequency domain representation of the original function • The original function is often a function in the Time domain • In image Processing the original function is in the Spatial Domain • The term Fourier transform can refer to either the Frequency domain representation of a function or to the process/formula that "transforms" one function into the other.

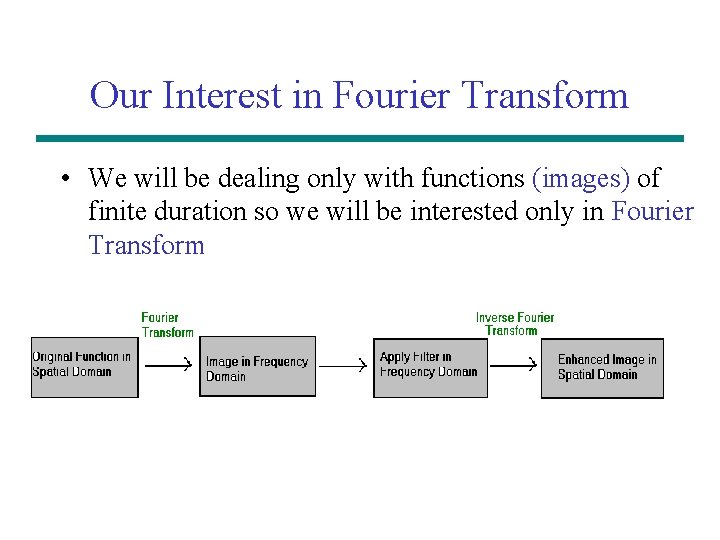
Our Interest in Fourier Transform • We will be dealing only with functions (images) of finite duration so we will be interested only in Fourier Transform

Applications of Fourier Transforms § § 1 -D Fourier transforms are used in Signal Processing 2 -D Fourier transforms are used in Image Processing 3 -D Fourier transforms are used in Computer Vision Applications of Fourier transforms in Image processing: – – – Image enhancement, Image restoration, Image encoding / decoding, Image description

One Dimensional Fourier Transform and its Inverse § The Fourier transform F (u) of a single variable, continuous function f (x) is § Given F(u) we can obtain f (x) by means of the Inverse Fourier Transform

Discrete Fourier Transforms (DFT) 1 -D DFT for M samples is given as The Inverse Fourier transform in 1 -D is given as

Discrete Fourier Transforms (DFT) 1 -D DFT for M samples is given as The inverse Fourier transform in 1 -D is given as

Two Dimensional Fourier Transform and its Inverse § The Fourier transform F (u, v) of a two variable, continuous function f (x, y) is § Given F(u, v) we can obtain f (x, y) by means of the Inverse Fourier Transform

2 -D DFT

Fourier Transform

2 -D DFT

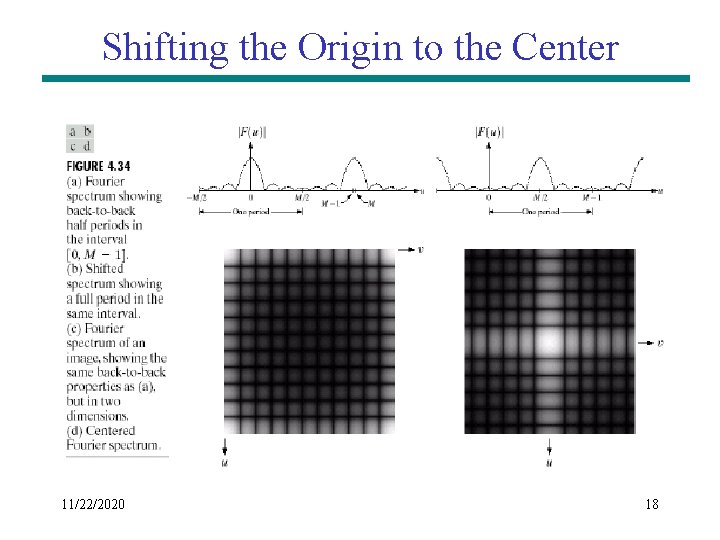
Shifting the Origin to the Center 11/22/2020 17

Shifting the Origin to the Center 11/22/2020 18

Properties of Fourier Transform § The lower frequencies corresponds to slow gray level changes § Higher frequencies correspond to the fast changes in gray levels (smaller details such edges of objects and noise) 11/22/2020 19

DFT Examples 11/22/2020 20

DFT Examples 11/22/2020 21

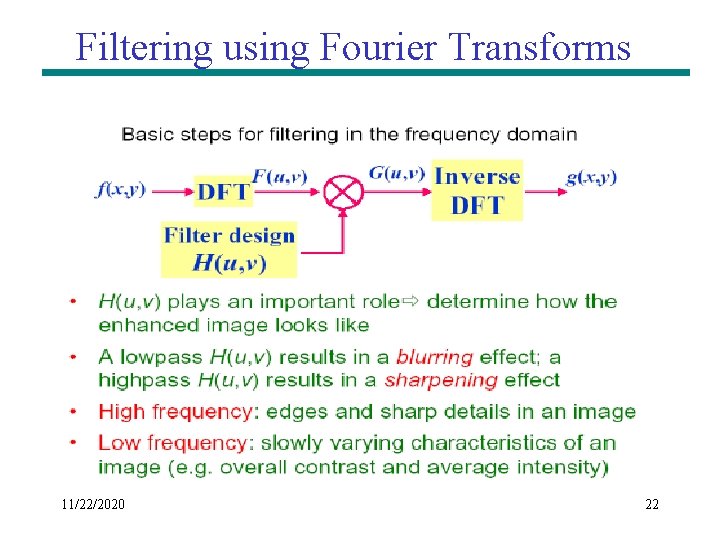
Filtering using Fourier Transforms 11/22/2020 22

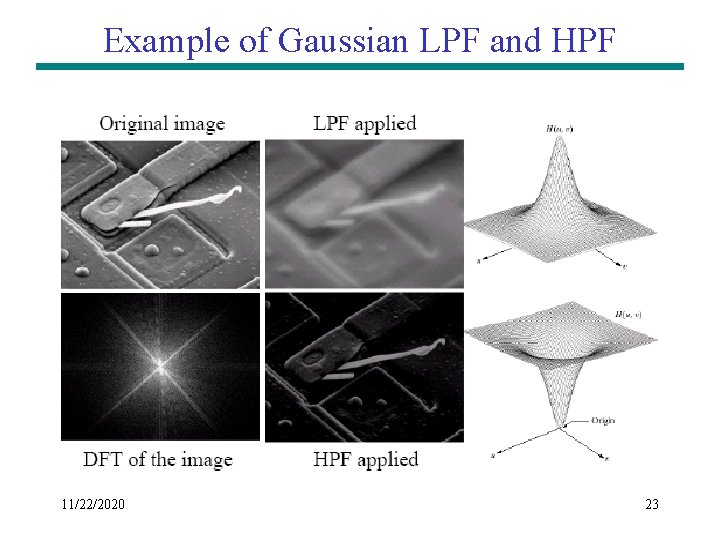
Example of Gaussian LPF and HPF 11/22/2020 23

Filters to be Discussed 11/22/2020 24

Low Pass Filtering A low-pass filter attenuates high frequencies and retains low frequencies unchanged. The result in the spatial domain is equivalent to that of a smoothing filter; as the blocked high frequencies correspond to sharp intensity changes, i. e. to the fine-scale details and noise in the spatial domain image. 11/22/2020 25

High Pass Filtering A highpass filter, on the other hand, yields edge enhancement or edge detection in the spatial domain, because edges contain many high frequencies. Areas of rather constant gray level consist of mainly low frequencies and are therefore suppressed. 11/22/2020 26

Band Pass Filtering A bandpass attenuates very low and very high frequencies, but retains a middle range band of frequencies. Bandpass filtering can be used to enhance edges (suppressing low frequencies) while reducing the noise at the same time (attenuating high frequencies). Bandpass filters are a combination of both lowpass and highpass filters. They attenuate all frequencies smaller than a frequency Do and higher than a frequency D 1 , while the frequencies between the two cut-offs remain in the resulting output image. 11/22/2020 27

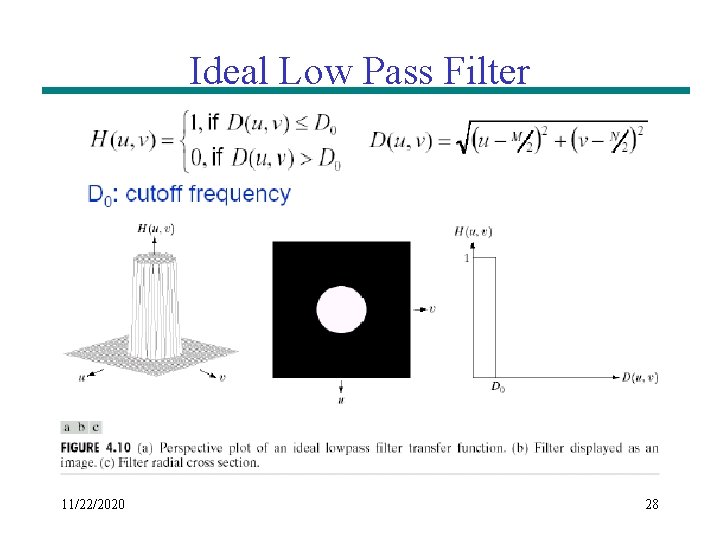
Ideal Low Pass Filter 11/22/2020 28

Ideal Low Pass Filter 11/22/2020 29

Ideal Low Pass Filter (example) 11/22/2020 30

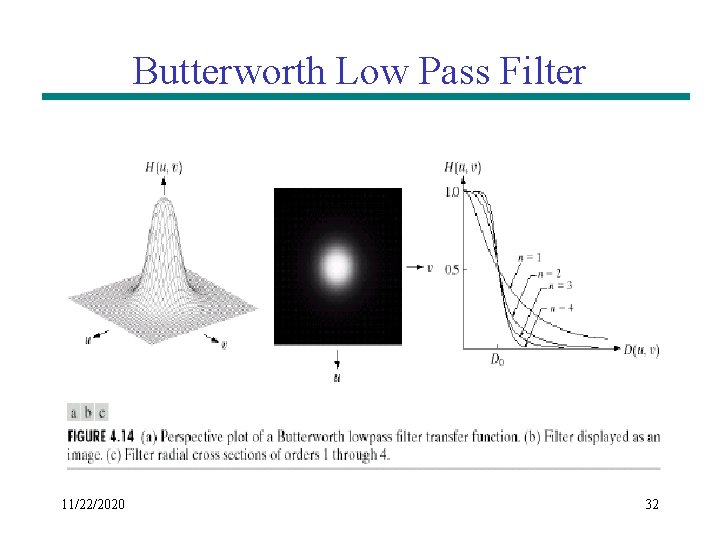
Butterworth Low Pass Filter 11/22/2020 31

Butterworth Low Pass Filter 11/22/2020 32

Butterworth Low Pass Filter (example) 11/22/2020 33

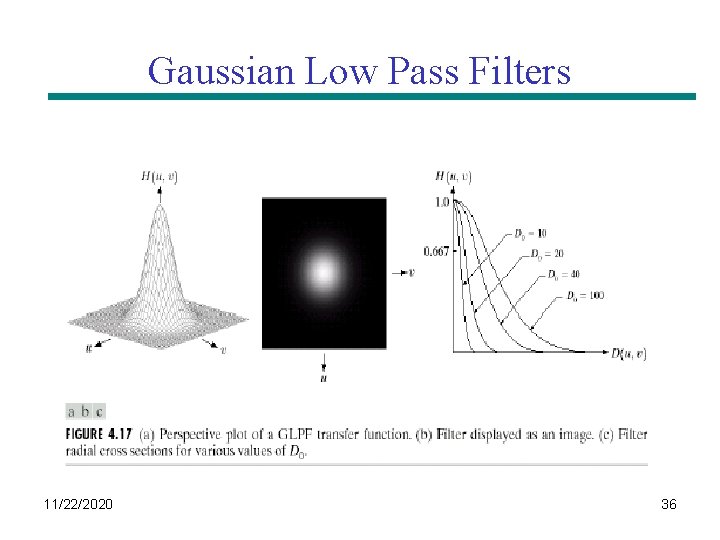
Gaussian Low Pass Filters 11/22/2020 34

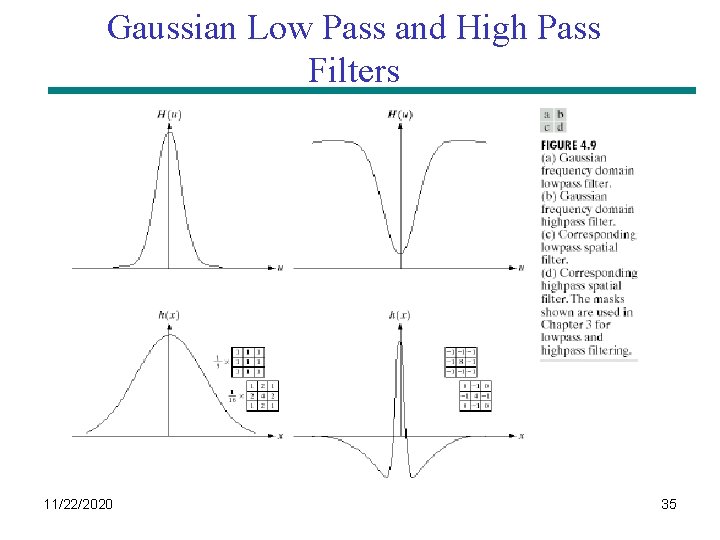
Gaussian Low Pass and High Pass Filters 11/22/2020 35

Gaussian Low Pass Filters 11/22/2020 36

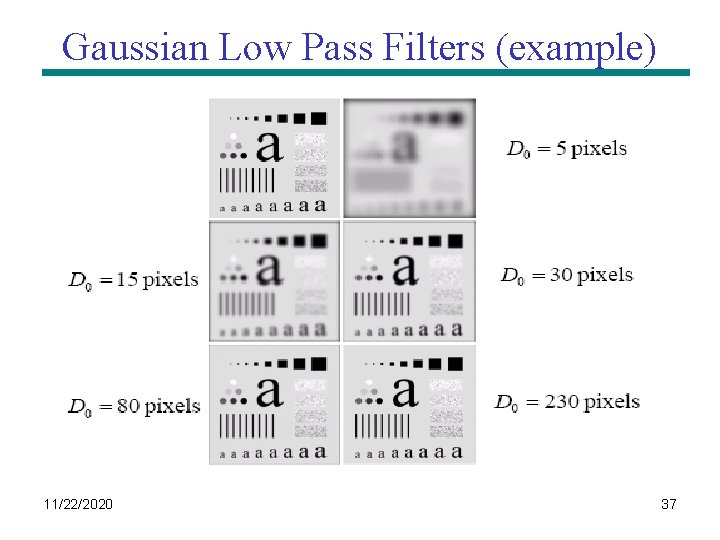
Gaussian Low Pass Filters (example) 11/22/2020 37

Gaussian Low Pass Filters (example) 11/22/2020 38

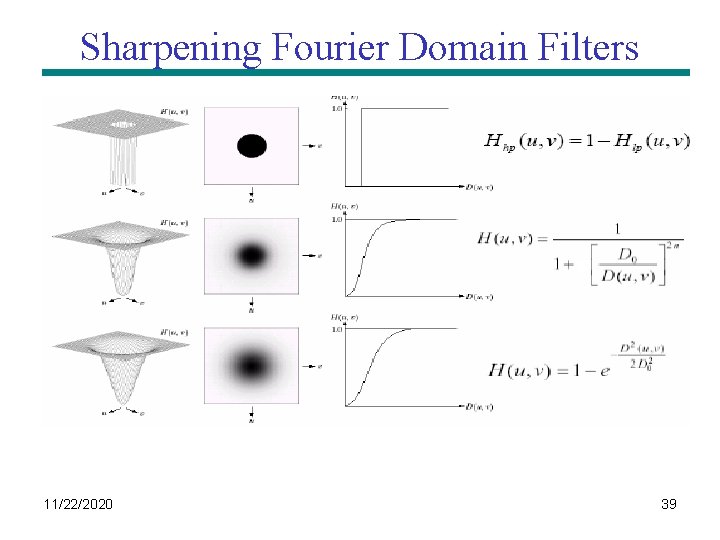
Sharpening Fourier Domain Filters 11/22/2020 39

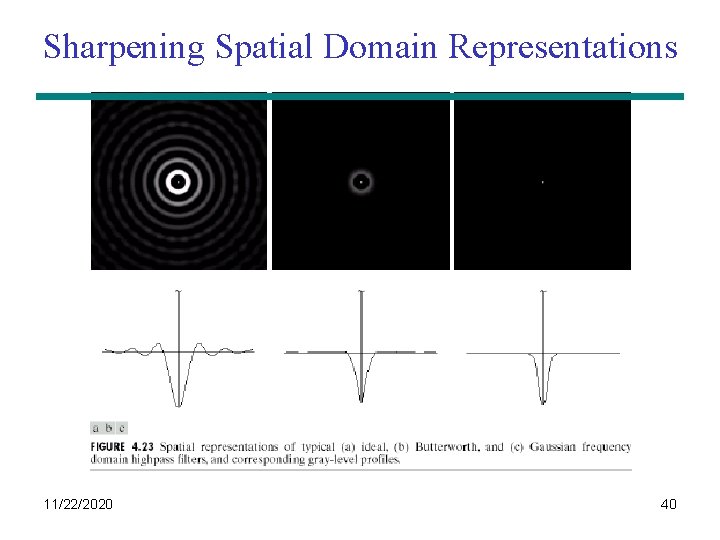
Sharpening Spatial Domain Representations 11/22/2020 40

Sharpening Fourier Domain Filters (Examples) 11/22/2020 41

Sharpening Fourier Domain Filters (Examples) 11/22/2020 42

Sharpening Fourier Domain Filters (Examples) 11/22/2020 43