Digital Design Fundamentals Basic Logic Gates Logic Function

Digital Design Fundamentals

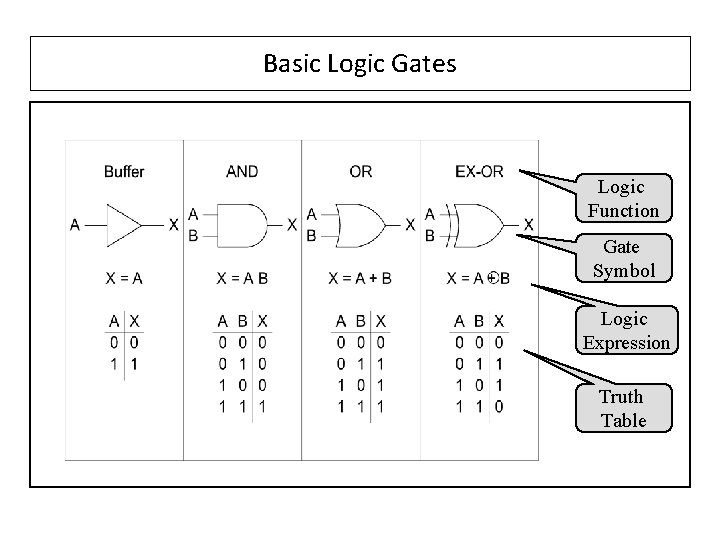
Basic Logic Gates Logic Function Gate Symbol Logic Expression Truth Table

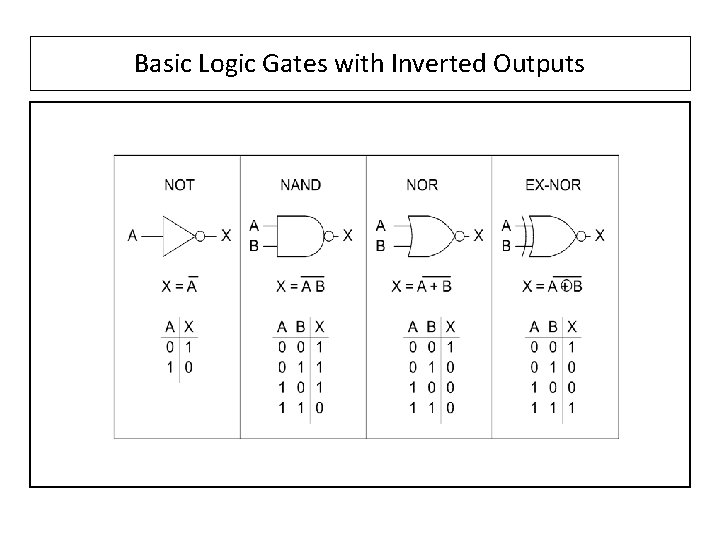
Basic Logic Gates with Inverted Outputs

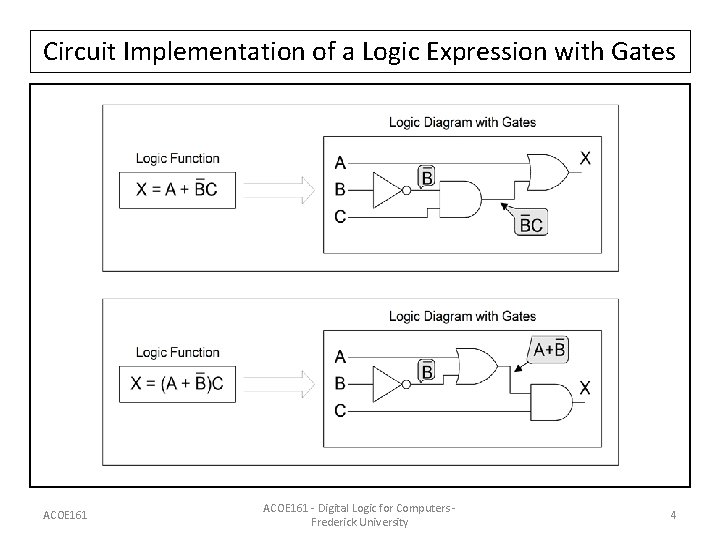
Circuit Implementation of a Logic Expression with Gates ACOE 161 - Digital Logic for Computers Frederick University 4

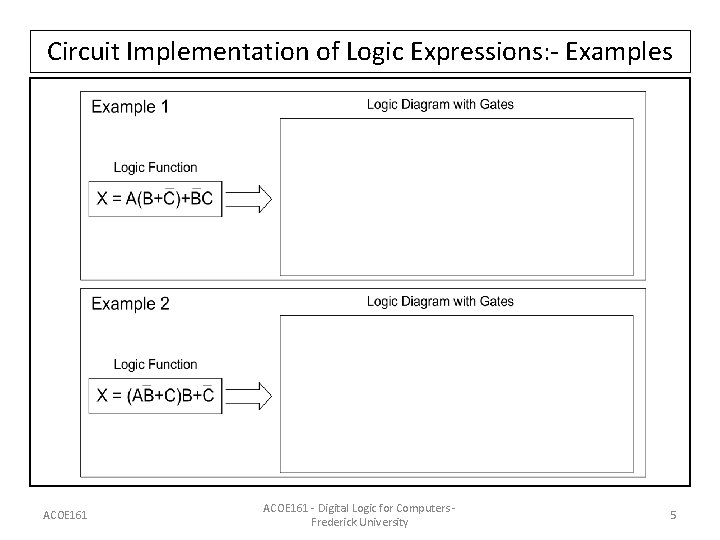
Circuit Implementation of Logic Expressions: - Examples ACOE 161 - Digital Logic for Computers Frederick University 5

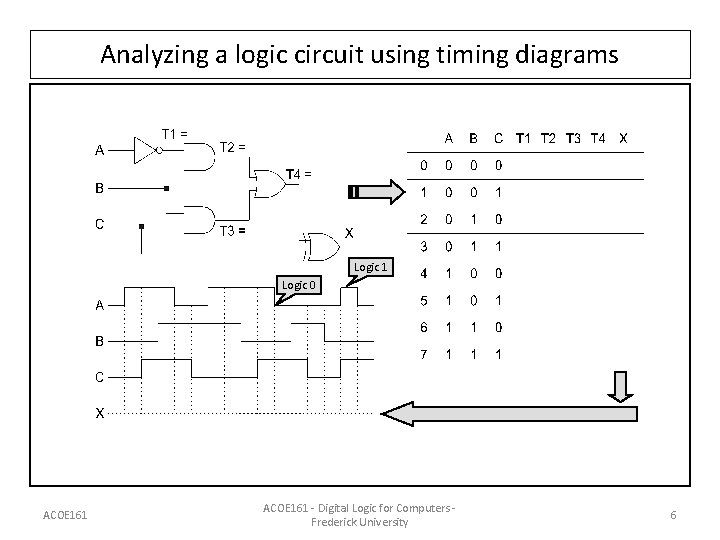
Analyzing a logic circuit using timing diagrams Logic 1 Logic 0 ACOE 161 - Digital Logic for Computers Frederick University 6

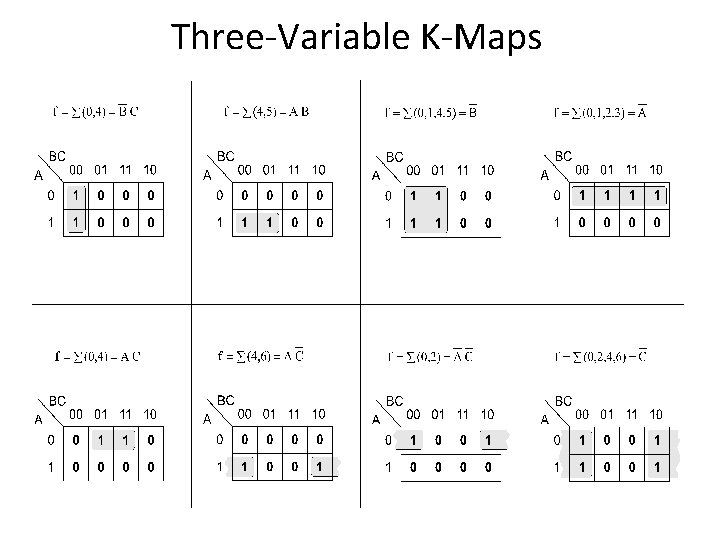
Three-Variable K-Maps

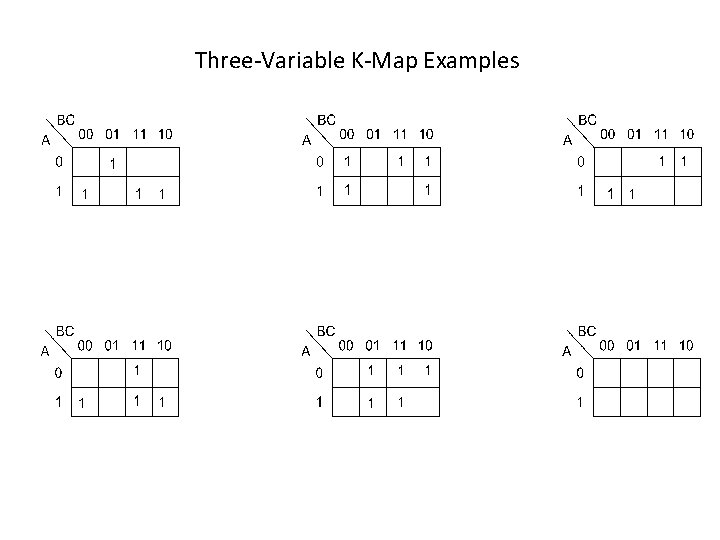
Three-Variable K-Map Examples

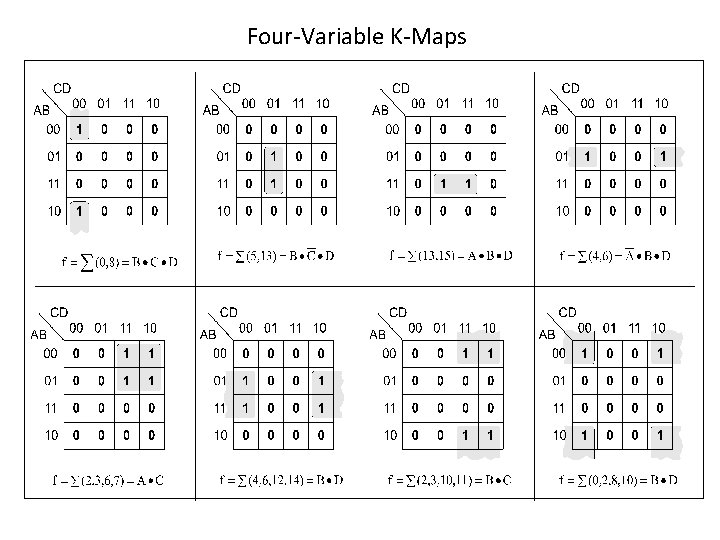
Four-Variable K-Maps

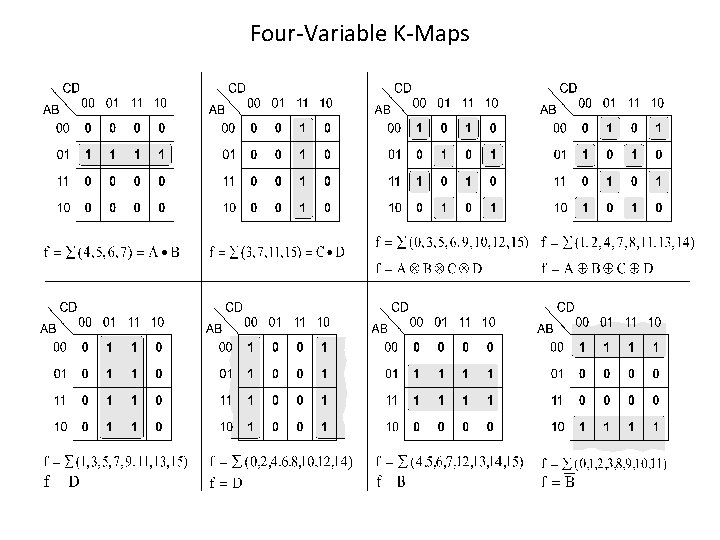
Four-Variable K-Maps

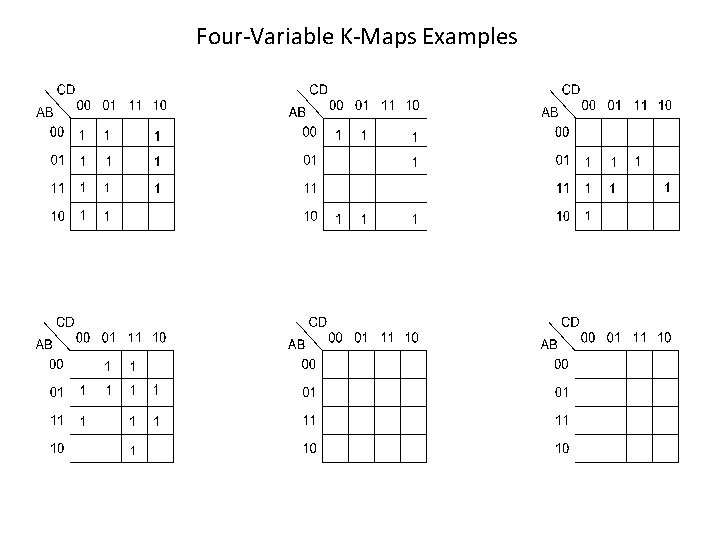
Four-Variable K-Maps Examples

Don’t Care Conditions • In many application it is known in advance that some of the input combinations will never occur. These combinations are marked as “Don’t Care Conditions” and are used as either zero’s or one’s so that the application is implemented with the most simplified circuit. • Example: Simplify the logic expression X(A, B, C, D) with the don’t care conditions d(A, B, C, D). ACOE 161 - Digital Logic for Computers Frederick University 12

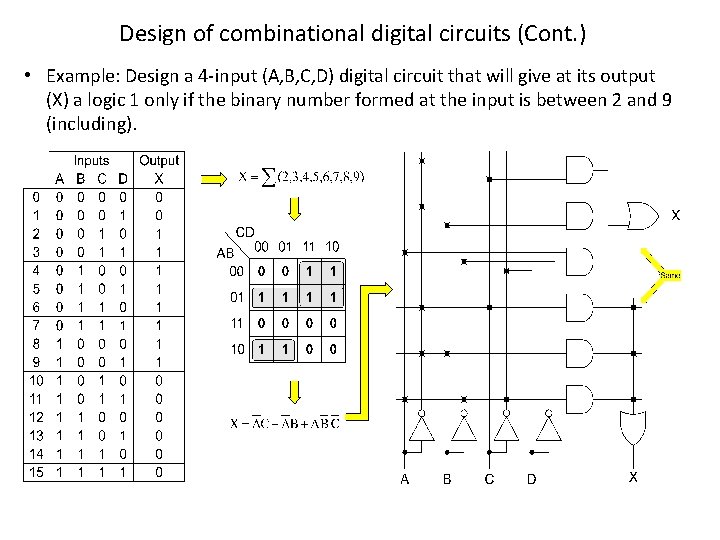
Design of combinational digital circuits (Cont. ) • Example: Design a 4 -input (A, B, C, D) digital circuit that will give at its output (X) a logic 1 only if the binary number formed at the input is between 2 and 9 (including).

Don’t Care Conditions: Examples ACOE 161 - Digital Logic for Computers Frederick University 14

Revision on MSI Devices M. Mano & C. Kime: Logic and Computer Design Fundamentals (Chapter 5)

MSI Devices • Medium Scale Integration (MSI) devices are digital devices that are build using a few tens to hundreds of logic gates. • MSI devices are used as discrete devices packed in a single Integrated Circuit (IC), or as building blocks for other, more complex devices such as memory devices or microprocessors. • Some typical MSI devices are the following: – Encoders and Decoders – Multiplexers and Demultiplexers – Full Adders – Latches and flip flops – Registers and Counters

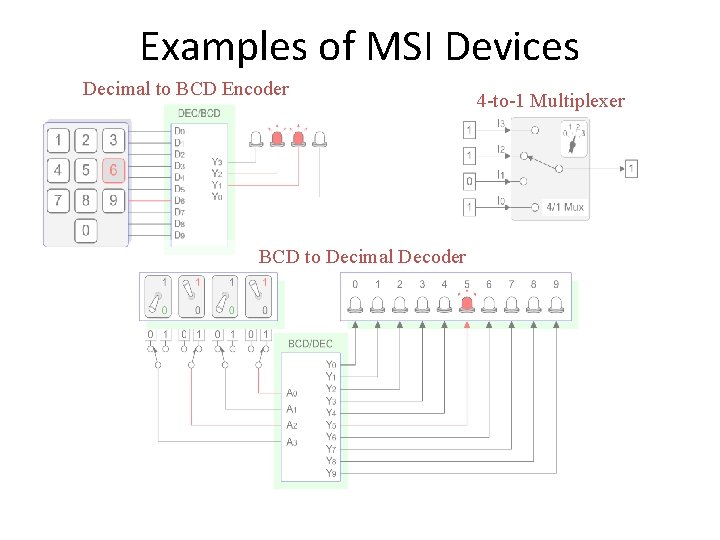
Examples of MSI Devices Decimal to BCD Encoder BCD to Decimal Decoder 4 -to-1 Multiplexer

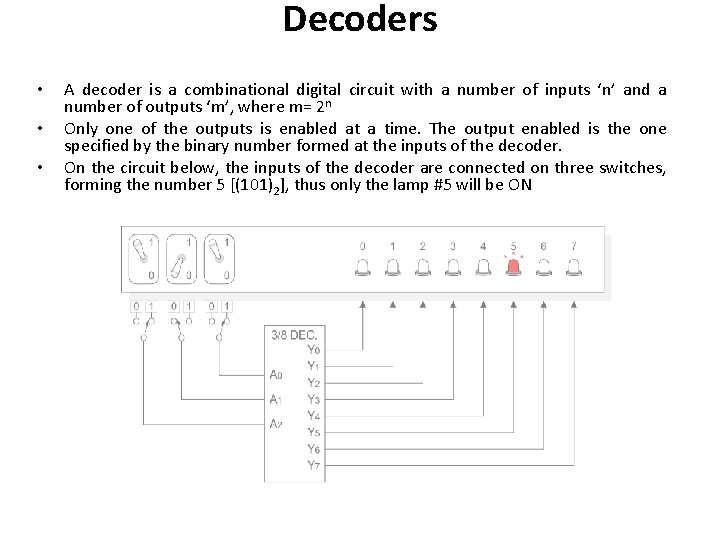
Decoders • • • A decoder is a combinational digital circuit with a number of inputs ‘n’ and a number of outputs ‘m’, where m= 2 n Only one of the outputs is enabled at a time. The output enabled is the one specified by the binary number formed at the inputs of the decoder. On the circuit below, the inputs of the decoder are connected on three switches, forming the number 5 [(101)2], thus only the lamp #5 will be ON

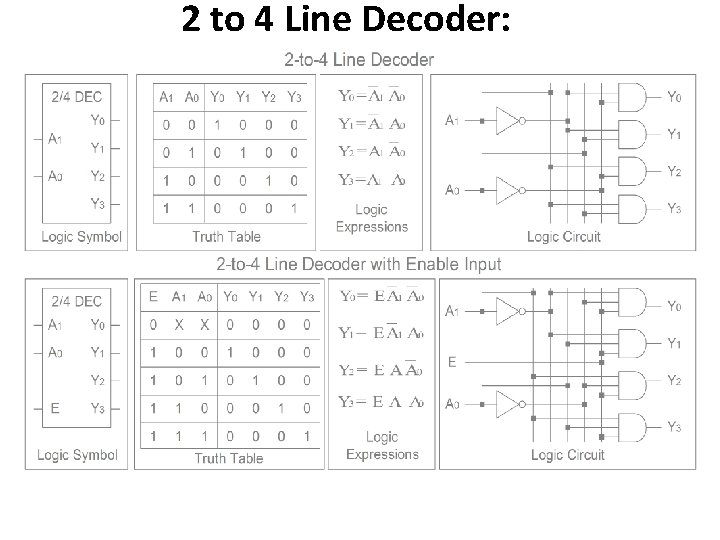
2 to 4 Line Decoder:

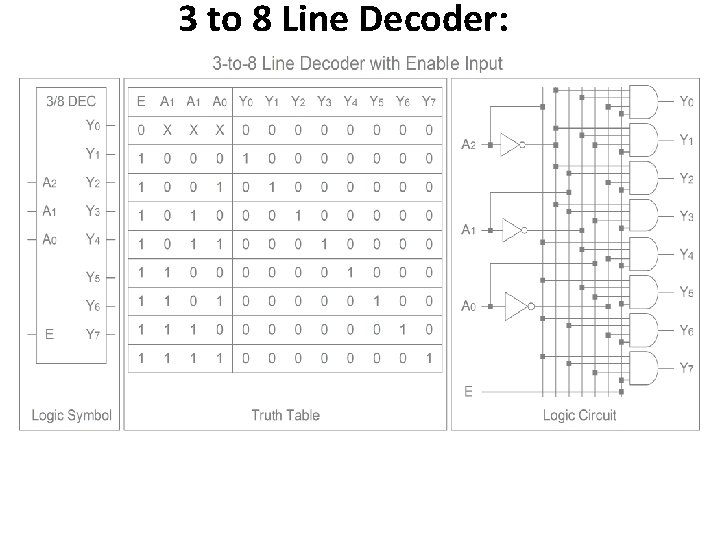
3 to 8 Line Decoder:

Multiplexers • A multiplexer is a device that has a number of data inputs “m”, and number of control inputs “n” and one output, such that m=2 n. The output has always the same value as the data input specified by the binary number at the control inputs. • The rotary switch (selector) shown in figure (a) below, is equivalent to a 4 -to-1 multiplexer. • The sliding switch shown in figure (b) below, is equivalent to an 8 -to-1 multiplexer.

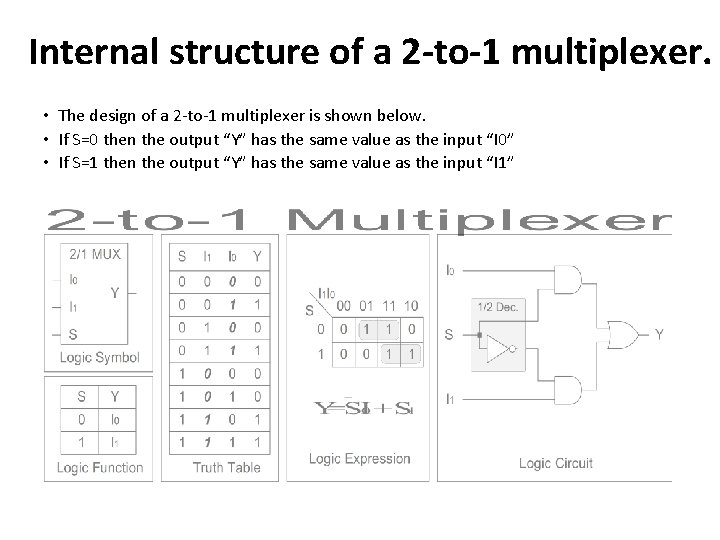
Internal structure of a 2 -to-1 multiplexer. • The design of a 2 -to-1 multiplexer is shown below. • If S=0 then the output “Y” has the same value as the input “I 0” • If S=1 then the output “Y” has the same value as the input “I 1”

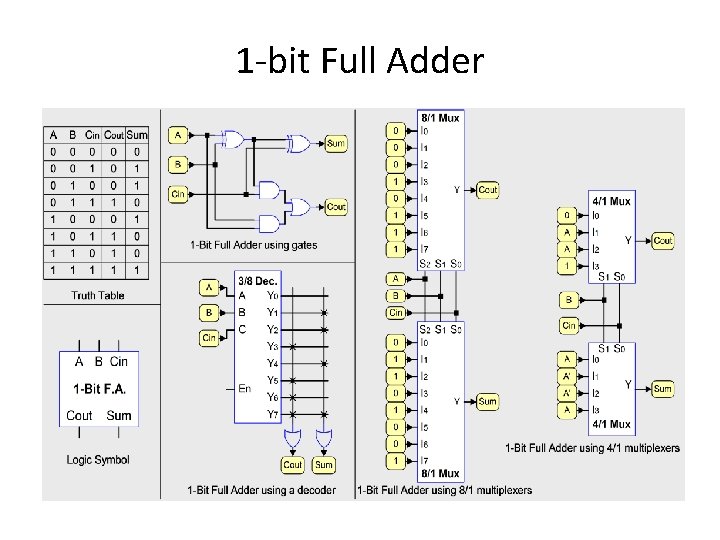
1 -bit Full Adder

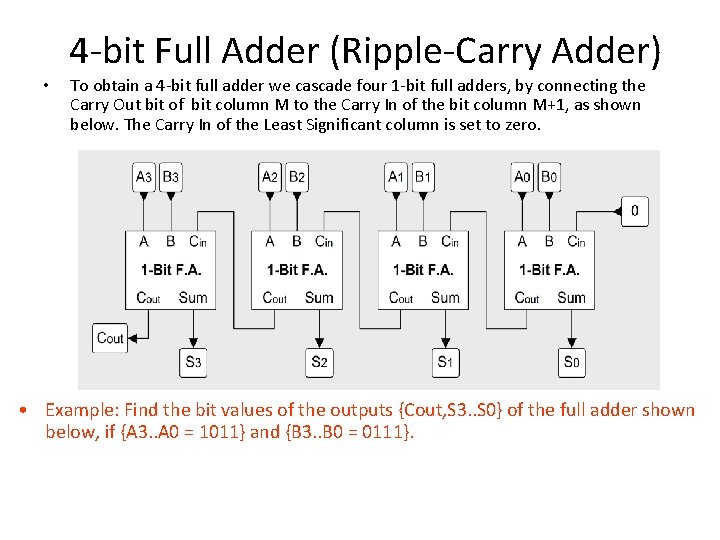
4 -bit Full Adder (Ripple-Carry Adder) • To obtain a 4 -bit full adder we cascade four 1 -bit full adders, by connecting the Carry Out bit of bit column M to the Carry In of the bit column M+1, as shown below. The Carry In of the Least Significant column is set to zero. • Example: Find the bit values of the outputs {Cout, S 3. . S 0} of the full adder shown below, if {A 3. . A 0 = 1011} and {B 3. . B 0 = 0111}.

Magnitude Comparator

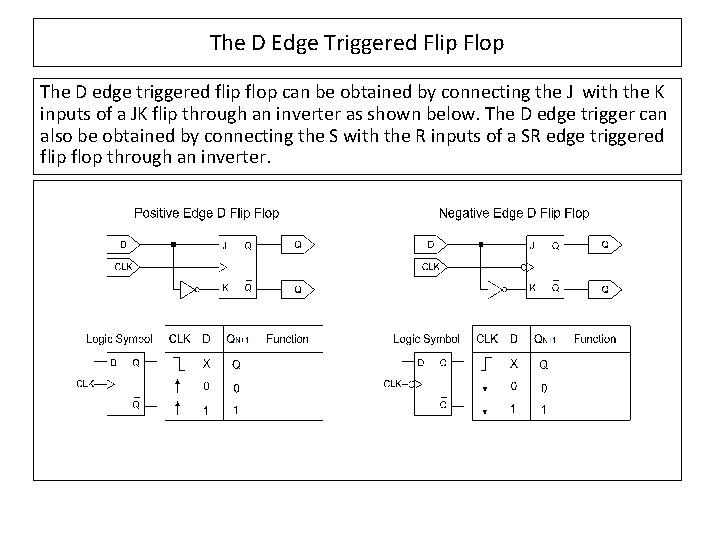
The D Edge Triggered Flip Flop The D edge triggered flip flop can be obtained by connecting the J with the K inputs of a JK flip through an inverter as shown below. The D edge trigger can also be obtained by connecting the S with the R inputs of a SR edge triggered flip flop through an inverter.

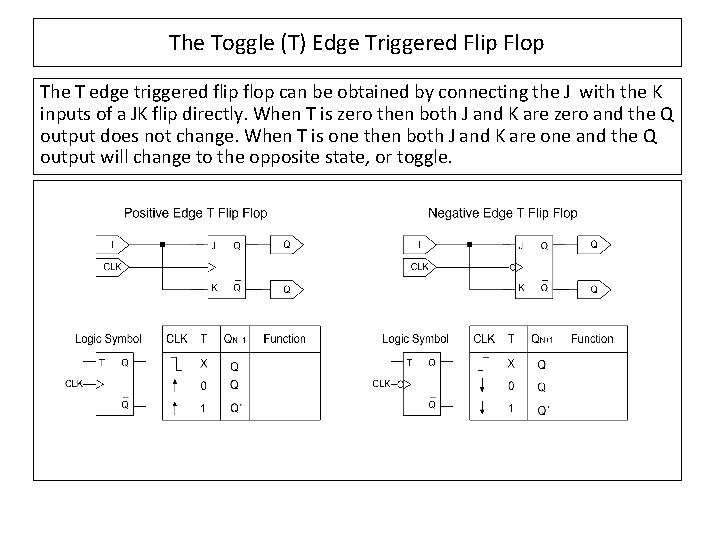
The Toggle (T) Edge Triggered Flip Flop The T edge triggered flip flop can be obtained by connecting the J with the K inputs of a JK flip directly. When T is zero then both J and K are zero and the Q output does not change. When T is one then both J and K are one and the Q output will change to the opposite state, or toggle.

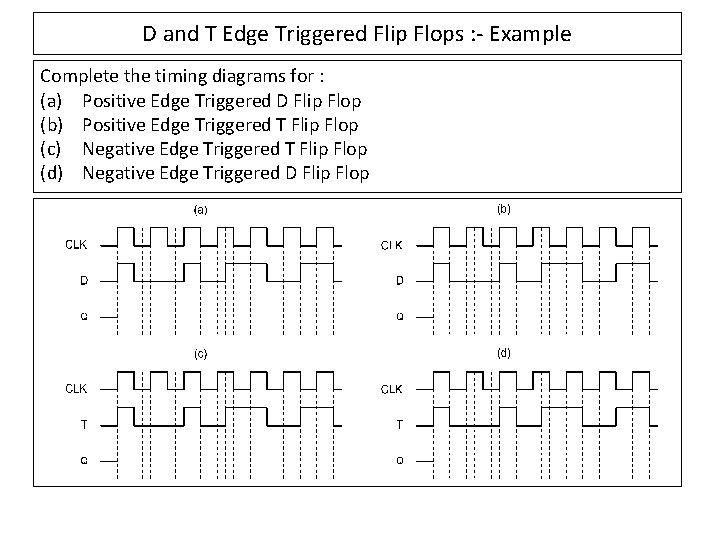
D and T Edge Triggered Flip Flops : - Example Complete the timing diagrams for : (a) Positive Edge Triggered D Flip Flop (b) Positive Edge Triggered T Flip Flop (c) Negative Edge Triggered T Flip Flop (d) Negative Edge Triggered D Flip Flop

Flip Flops with asynchronous inputs (Preset and Clear) Two extra inputs are often found on flip flops, that either clear or preset the output. These inputs are effective at any time, thus are called asynchronous. If the Clear is at logic 0 then the output is forced to 0, irrespective of the other normal inputs. If the Preset is at logic 0 then the output is forced to 1, irrespective of the other normal inputs. The preset and the clear inputs can not be 0 simultaneously. In the Preset and Clear are both 1 then the flip flop behaves according to its normal truth table.

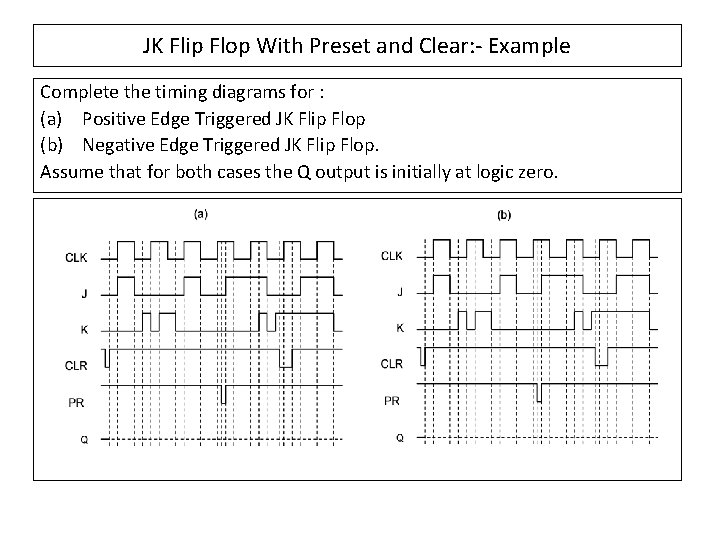
JK Flip Flop With Preset and Clear: - Example Complete the timing diagrams for : (a) Positive Edge Triggered JK Flip Flop (b) Negative Edge Triggered JK Flip Flop. Assume that for both cases the Q output is initially at logic zero.

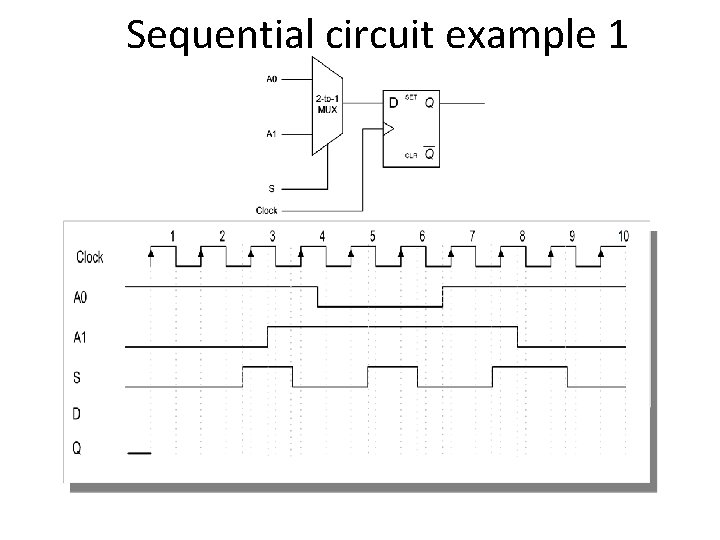
Sequential circuit example 1

Finite State Machine • A generic model for sequential circuits used in sequential circuit design ACOE 161 - Digital Logic for Computers Frederick University

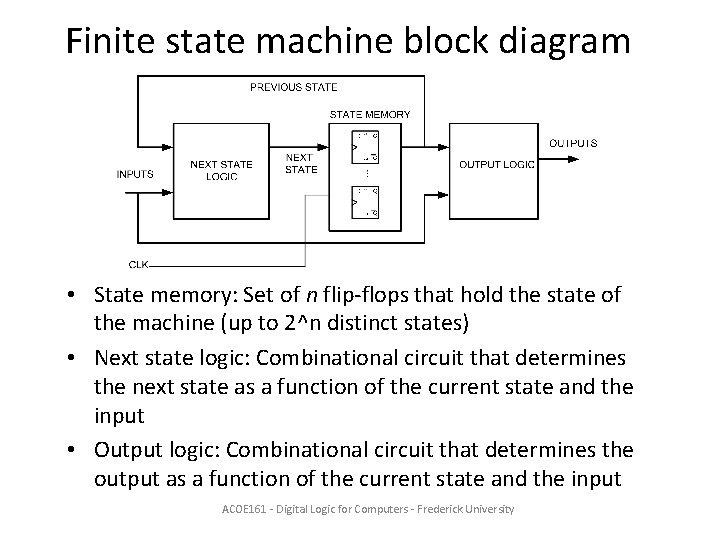
Finite state machine block diagram • State memory: Set of n flip-flops that hold the state of the machine (up to 2^n distinct states) • Next state logic: Combinational circuit that determines the next state as a function of the current state and the input • Output logic: Combinational circuit that determines the output as a function of the current state and the input ACOE 161 - Digital Logic for Computers - Frederick University

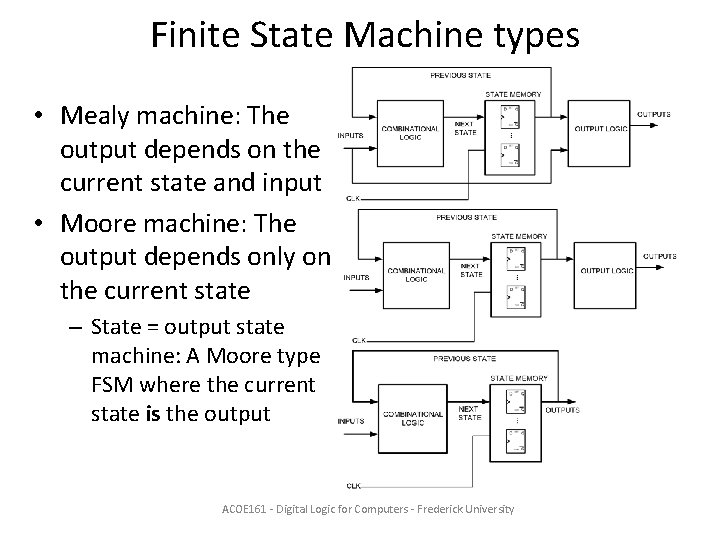
Finite State Machine types • Mealy machine: The output depends on the current state and input • Moore machine: The output depends only on the current state – State = output state machine: A Moore type FSM where the current state is the output ACOE 161 - Digital Logic for Computers - Frederick University

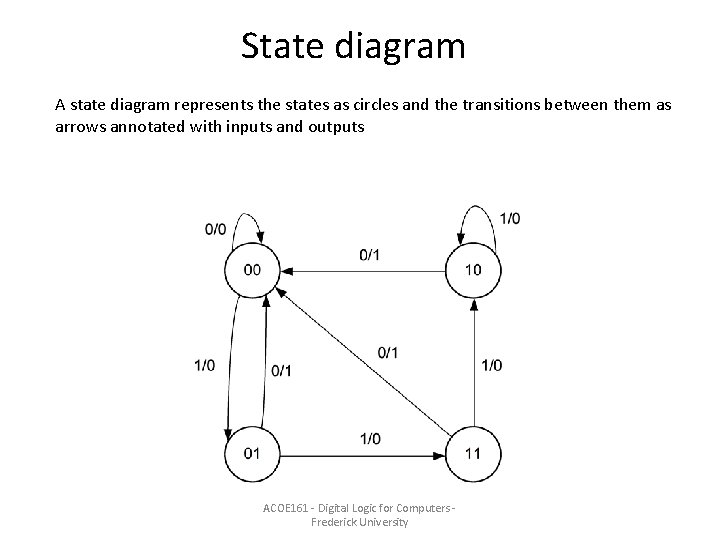
State diagram A state diagram represents the states as circles and the transitions between them as arrows annotated with inputs and outputs ACOE 161 - Digital Logic for Computers Frederick University

Analysis of FSMs with D flip-flops • Determine the next state and output functions • Use the functions to create a state/output table that specifies every possible next state and output for any combination of current state and input ACOE 161 - Digital Logic for Computers Frederick University

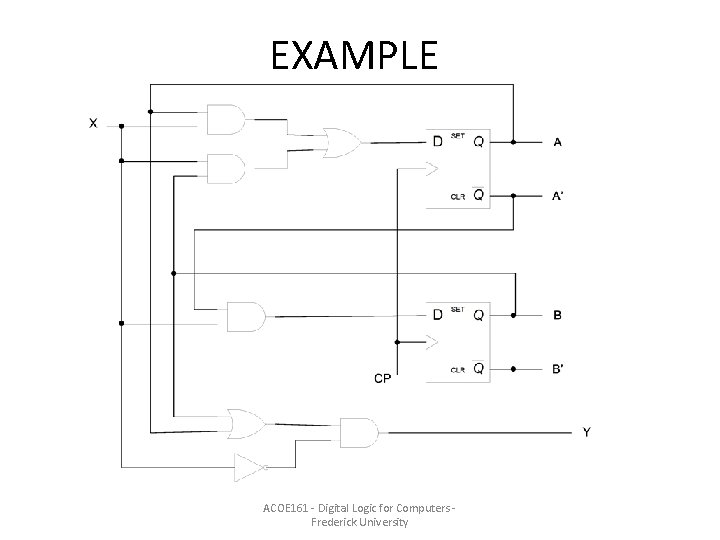
EXAMPLE ACOE 161 - Digital Logic for Computers Frederick University

Next state equations and state table for example • A+=Ax+Bx • B+=A΄x • Y=(A+B)x΄ A B x A+ B+ y 0 0 0 0 1 0 0 0 1 1 1 1 0 0 0 0 1 1 0 0 0 1 1 1 0 0 ACOE 161 - Digital Logic for Computers Frederick University

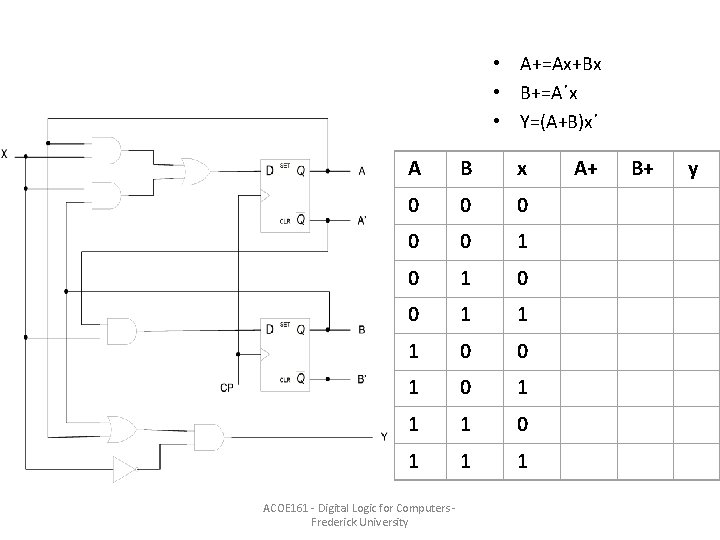
• A+=Ax+Bx • B+=A΄x • Y=(A+B)x΄ A B x 0 0 0 1 1 1 0 0 1 1 1 ACOE 161 - Digital Logic for Computers Frederick University A+ B+ y

Sequential circuit design methodology • From the description of the functionality or the state/timing diagram find the state table • Encode the states if the state table contains letters • Find the necessary number of flip-flops • Select flip/flop type • From the state table, find the excitation tables and output tables • Using Karnaugh maps find the flip-flop input logic expressions • Draw the circuit logic diagram ACOE 161 - Digital Logic for Computers Frederick University

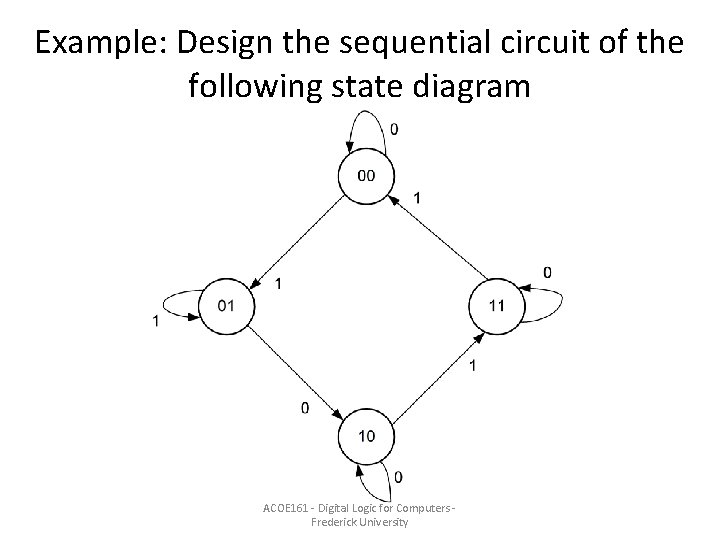
Example: Design the sequential circuit of the following state diagram ACOE 161 - Digital Logic for Computers Frederick University

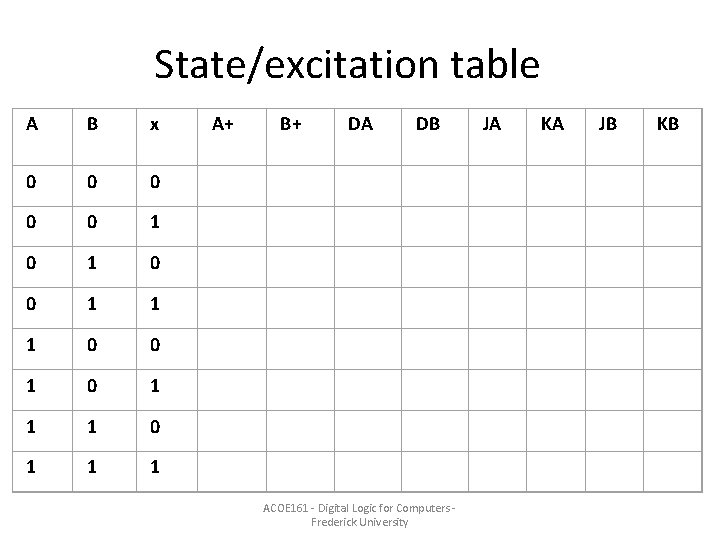
State/excitation table A B x 0 0 0 1 1 1 0 0 1 1 1 A+ B+ DA DB ACOE 161 - Digital Logic for Computers Frederick University JA KA JB KB

Karnaugh maps for combinational circuit ACOE 161 - Digital Logic for Computers Frederick University

Circuit logic diagram ACOE 161 - Digital Logic for Computers Frederick University